运动的独立性对于解决复杂曲线问题的误区与反思——基于物理核心素养的创新人才培养实践经验与启示

陈 斌

（福州第三中学，福建 福州 350001）

一、运动的独立性在物理教学中常见的误区

运动的合成与分解是解决复杂曲线问题的一种重要方法，如何把复杂的曲线运动分解为已知的简单运动是解决曲线运动问题的关键和难点，而这个过程的核心思想则依赖于运动的独立性。例如，在司南版《必修2》中指出，“一个复杂运动可以视为若干互不影响的独立的分运动”，并以平抛运动为例，通过实验说明小球“在竖直方向上的运动与水平方向上的运动互不影响，是相互独立的运动”。但是对于任何分运动是否具有独立性并没有说明，而是在教材中指出“这就是运动的独立性”。受此影响，许多教师在平时教学过程中，往往仅通过几类典型模型学生进行运动独立性的引导，以至于大部分的学生在无意识中都形成了“任何一个运动的两个分运动之间均具有独立性”的刻板印象。这种刻板印象的形成，不仅让学生在遇到一些复杂题目的时候很容易陷入思维定势从而找不出破题要点，更重要的是，仅通过个别案例得到的结论不假思索地推广成一个普遍性规律和原则，很容易让学生丧失独立思考和严密逻辑思维的能力，对于创新人才的培养是极为不利的。

因此，需要对“运动的独立性”进行更深入地分析，以发掘其更深刻的内部规律！

二、运动的独立性分析

（一）典例分析

2011年福建省理综卷第22题考查了带电粒子在复合场中的运动，尤其是对学生理解与运用运动的合成与分解，提出了比较高的要求。该题就运动的独立性问题而言，是一道有代表性的题目，限于篇幅，文章主要就第（2）问进行讨论。

（2011福建）（2）只改变入射粒子初速度的大小，发现初速度大小不同的粒子虽然运动轨迹（y—x曲线）不同，但具有相同的空间周期性，如图乙所示；同时，这些粒子在y轴方向上的运动（y—t关

Ⅰ．求粒子在一个周期T内，沿X轴方向前进的距离S。

Ⅱ．当入射粒子的初速度大小为V0时，其y—t图像如图丙所示，求该粒子在y轴方向上做简谐运动的振幅Ay，并写出y—t的函数表达式［1］。

解析 对于第（2）问的两个问题，可以按照牛顿运动定律列出一般式：

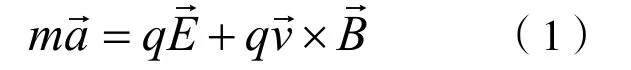
将带电粒子沿x和y两个方向分别列运动方程：

比较（2）（3）两式发现，水平方向的运动包含了竖直方向的运动分量，竖直方向也是如此，这表明两个方向上的分运动之间是相互影响的，这个结果与所谓的“运动的独立性”是相违背的。此时如果要求出x和y的随时间函数关系就需要去求解复杂的微分方程。

将（2）式对t求导并带入（3）式vy，消去，得到关于vx一元微分方程：

（二）运动独立性适用条件

上述分析表明，运动的独立性是有前提条件的，它是建立在分运动各自满足独立方程，彼此之间没有耦合项的基础上，因此并不存在“运动的独立作用原理”一说。实际上，通过查阅相关文献会发现“运动的独立作用原理” 来源于对力的独立性的错误推广，同时也是错误地把运用矢量分解研究问题的方法当作运动独立性原理的依据。［2］

在弄清楚了运动的独立性之后，就可以明白常见的物理模型中诸如平抛、带电粒子在匀强电场中的偏转，各个运动方向彼此无耦合项，在解题过程中其相关运动过程的物理量，例如加速度、速度、位移等，均可以分解到适宜的方向上，彼此之间相互独立。但是对于类似文章所涉及的带电粒子在复合场中的偏转，又或者空气阻力不能忽略的拋体运动等，一般情况下各运动分量之间是相互关联的，虽然依然可以运用运动的合成与分解的方法进行求解，但在实际求解过程中则要求解复杂的微分方程，此时往往需要通过一些巧妙的方法找到相互独立且比较简单的分运动加以简化计算。

（三）巧用运动独立性解决复杂曲线问题

当然，如果学会巧用运动的独立性，对于解题就会产生明显的效果。还是以上述高考题为例，这里介绍一种巧用运动独立性解题的方法。

必须指出的是，第二种方法虽然巧妙地将合运动分解为两个相对简单且独立的分运动，但是这并不意味这对每一种复杂运动都适用。但是考虑到第一种方法在计算上的复杂性，也明确了出题者在命题时候一般会给出这种可以独立分解的情况，那就可以给我们启发，如果在进行运动的合成与分解之前先对运动独立性进行分析，找到消除耦合项的约束条件，很多时候就可以像本题一样找到快速解决问题的突破口。

三、运动独立性分析对于教育教学的启示

笔者认为，教学的逻辑与思维的逻辑、学科的逻辑应当是一致的，对于结构性很强的物理学科，更应体现科学的逻辑性，这才是中学生应该具备的核心素养。

这就要求，在进行运动合成与分解这部分内容教学时，应注意厘清合运动与分运动之间内在的关系，是建立在物理矢量在物理学中是以矢量运算法则、直角坐标、极坐标、自然坐标、球坐标、柱坐标等一整套数学体系基础上表达出来的结果。［4］在教学过程中不能简单将平抛或蜡块等实验的结果作为分运动独立性的依据，而要引导学生思考为什么运动的合成与分解要提出独立性要求，什么情况下能够满足独立性要求。要深入挖掘如何分解才能够满足“简便”这一教学过程中的重要逻辑枢纽，而分运动的独立性正是在这一逻辑下的自然延伸，就如在案例分析中，正是考虑到分运动的独立性，才可以避开求解繁琐的微分方程，从而达到“简便”的目的。学生知识逻辑的形成，尤其需要教师依据物理学的学科结构以及学生认知结构不断去渗透与构建。

学生科学思维能力的形成，是培养创新人才最核心的要素之一。从学生知识建构的逻辑性出发，克服运动独立性教学过程中的一些常见误区，这是对基于核心素养的创新人才实践的一种有益探索。

［1］福建理科综合能力测试物理试题部分及参考答案［J］． 中学物理教学参考，2011（7）．

［2］杨习志，刘劲松．运动具有独立性原理吗［J］．物理教学，2015（11）．

［3］胡宗仁．“配速法”及其应用［J］,中学物理，2011（1）．

［4］胡扬洋．对“运动的独立性”与“力的独立作用原理”的再认识——兼论“平抛运动”教学的逻辑［J］．物理通报，2013（7）．