基于Logistic-Volterra模型的制造企业与物流企业联动发展稳定性分析

王珍珍, 吴英杰

(1.福建师范大学 经济学院，福州 350007；　2.福州大学 数学与计算机科学学院，福州 350116 )(*通信作者电子邮箱w0701860@163.com)

0　引言

市场竞争的加剧、国家政策的支持、物流技术和物流管理的日趋成熟使得全球供应链管理中的制造企业越来越倾向于通过主辅分离而选择物流外包的方式。2017年8月17日，国务院办公厅发布了《关于进一步推进物流降本增效促进实体经济发展的意见》，明确指出“推动物流业与制造业联动发展。研究制定推进物流业与制造业融合发展的政策措施，大力支持第三方物流发展，对接制造业转型升级需求，提供精细化、专业化物流服务，提高企业运营效率。鼓励大型生产制造企业将自营物流面向社会提供公共物流服务。”[1]Giri等[2]也指出第三方物流在今天的供应链管理中扮演着重要的角色，物流外包已经作为企业降低成本和提高运作弹性的重要手段而广泛运用于社会生产服务过程中。但在调研过程中发现，我国物流成本占GDP的比重仍然高达16.1%，是发达国家的两倍还多[3]。由于现有物流企业为数众多，但总体规模较小，物流供给领域的结构性矛盾依然存在，导致物流服务水平、信息化、标准化水平较低，制造企业与物流企业之间缺乏交流平台导致制造企业不愿意将物流环节外包而选择自营物流的模式，两者之间联动发展程度偏低。据统计，我国制造企业物流外包比例大概在20%左右[4]，大量的自营物流模式的存在将在一定程度上对物流企业的发展构成威胁。那么物流企业适应当今社会发展的需要，更好地满足制造企业发展需求，提升自身的服务层次，及时调整自身的发展策略，构成了物流企业未来发展的利益源泉。

1　相关工作与问题提出

关于制造企业与物流企业联动发展问题的探讨更多是从微观物流的视角切入。蒋志方等[5]给出了一个制造车间内物流系统仿真的模型-视图-控制器(Model View Controller， MVC)方法；刘小群等[6]基于多代理技术和互联网技术构建了制造企业将物流外包的信息支持系统；Colledani等[7]着重指出制造企业生产线上的质量控制对生产物流绩效有重要影响；Cheng等[8]以台湾TFT-LCD产业为例运用系统决策方法，分析了逆向物流对高科技制造企业供应链战略的重要影响；Trappey等[9]提出了提高物流企业全球运营效率的物流枢纽集成模型；Colovic[10]分析了物流企业与服装制造业开展合作的重大现实意义；Lai等[11]分析了中国出口制造企业进行绿色物流管理的生态现代化意义；Wilfried等[12]指出铁路车辆制造业将影响物流链配置模式的构建；Jonrinaldi等[13]提出了一个能够协调集成生产、库存周期、逆向物流的模型；Bonney等[14]介绍了一种帮助识别系统中的制造业物流问题的方法以确定组织的需求；Bouzon等[15]运用解释结构模型分析了巴西机械制造行业中的逆向物流问题；Azadian等[16]基于改进调度和整合运输规划的承诺交货模型研究了订单生产商寻求系统集成的运作问题；Pour等[17]系统性分析了增材制造技术(Additive Manufacturing Technology)和传统技术的差别，并探讨了在增材技术运用过程中的生产、分布和物流问题。以上研究主要是从微观视角出发，基于双方的合作关系展开的，然而，在当前制造企业自营物流仍然占有相当比例的情况下，竞争要素占有相当重要的成分，制造企业供应链的整合和效率的提升在很大程度上需要物流企业提供更为智能化的系统，以降低其对制造企业发展的制约。因此，在合作的基础上考虑制造企业与物流企业对彼此的竞争关系能够更加切合实际地反映现实问题。

2　Logistic-Volterra模型的构建及求解

为了解决这一问题，本文拟在传统的阻滞增长模型Logistic的基础上引入贡献系数和竞争系数，提出一个改进的Logistic-Volterra模型，并基于该模型研究分析制造企业与物流企业在合作与竞争并存的情况下系统达到均衡点的条件及其现实解释；然后利用数值模拟的方式分析模型达到稳定性解的影响因素以及模型改进前后对系统产出值的影响；最后通过实例研究的方式引入制造企业A和物流企业B，分析两者在合作过程中的竞争行为的体现以及竞合关系的存在对双方利益的影响。

本文所构建的Logistic-Volterra模型是在传统的Logistic增长模型基础上形成的，笔者在前期的研究过程中也基于Logistic增长模型对制造企业与物流企业的联动模式进行了初步的探讨[18]，在已有研究的基础上，本文将从数理上论证制造企业与物流企业达到稳定性解的数学条件，并通过数值模拟的方式进行了广泛的验证。在模型构建过程中运用到的相关变量符号及含义如表1所示。

表1　模型相关变量符号及含义说明Tab. 1　Related variables, symbols and meanings of the model

2.1　制造企业与物流企业联动发展的合作模型构建

传统的指数增长模型认为生物群体的增长可以获得无限的生长条件，但现实生活中由于受到有限资源环境的制约，种群数量的增长会有一个上限，种群增长率会随着种群数量的增加而逐渐减小，即资源环境对种群数量增长是有“阻滞”作用的，著名生物数学家Pierre Francois Verhulst将其称为阻滞增长模型，又称为Logistic模型[19]，其已被广泛运用于生物学、经济学和管理学等诸多领域。制造企业与物流企业作为两大物种，其增长满足Logistic模型，如式(1)和(2)所示：

(1)

(2)

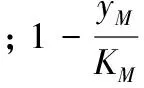
伴随着《物流产业调整振兴规划》将制造业与物流业联动列为“九大工程”之一，两业联动发展的呼声越来越高。一般情况下，在联动发展过程中，制造企业占据主导地位，制造企业的存在为物流企业订单的生成提供了广阔的市场空间，假定制造企业对物流企业的贡献度为δML，而物流企业依托于制造企业而存在，如果没有制造企业的增长，物流企业的产出水平将逐渐较少并趋于零，物流企业通过为制造企业提供资源、技术、服务、管理等因素参与到联动发展过程中，物流企业对制造企业的贡献度为δLM。因此，在考虑了制造企业与物流企业对彼此的贡献度的情况下，式(1)和(2)进一步地发展成为式(3)和(4)的表达式：

(3)

(4)

2.2　Logistic-Volterra模型的构建

当然，任何事物都存在着相互制约的关系。一方面，当制造企业不愿意将物流环节外包时，制造企业内部物流运作模式与物流企业在一定程度上构成了竞争关系CML；另一方面，由于社会上出现大量的物流企业，导致原先制造企业内部的物流运作模式面临着一定程度的威胁，或者即便是制造企业选择了物流外包的形式，但由于物流企业自身的服务层次较低，满足不了制造企业发展提出的需求时，物流企业给制造企业发展所带来的竞争系数为CLM。因此，单纯的Logistic增长模型并不足以说明两者之间的关系，在Logistic模型的基础上，构建了制造企业与物流企业的种间竞争模型(Lotka-Volterra模型)，如式(5)和(6)所示：

(5)

(6)

在式(3)～(6)的基础上，当同时考虑制造企业与物流企业对彼此的贡献和竞争系数时，制造企业最终的产出水平可以表示为：

(7)

此处假设δLM>CLM，即贡献系数大于竞争系数，否则就没有联动发展的必要。

物流企业最终的产出水平可以表示为：

(8)

此处，仍然假定δML>CML，即贡献系数大于竞争系数，否则就没有联动发展的必要。

将式(7)和(8)转化为如下的微分方程组，也就是本文所构建的Logistic-Volterra模型，即Logistic增长模型和Lotka-Volterra模型的结合体：

2.3　Logistic-Volterra模型求解

根据式(7)和(8)所构成的微分方程组可以得到四个平衡点P1(KM,0)，P2(0,-KL)，P3(0,0)以及P4,其中P4如下所示：

对于此处的平衡点而言是否属于稳定性的均衡点，可以通过构建雅克比矩阵[20]进行判断，分别将上述四个均衡点代入雅克比矩阵行列式和迹的表达式中，具体求解得到的值的表达式如表2所示。

表2　制造企业与物流企业联动发展稳定性均衡点求解Tab. 2　Stability equilibrium solution of interactive development of manufacturing and logistics enterprises

当均衡点在P4时，其矩阵行列式的值为：

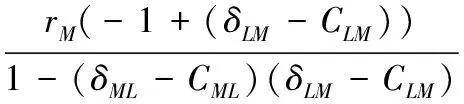
矩阵的迹为：

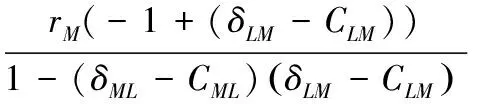
只有当平衡点位于平面坐标系的第一象限时，产出水平才有意义，因此前面三个平衡点不予考虑，当P4达到平衡点时，根据微分方程稳定性的判定方法，满足P4为均衡点的条件是：0<(δLM-CLM)<1，(δLM-CLM)>1，0<(δLM-CLM)(δML-CML)<1。由此得出本文的定理1：

定理1设0<(δLM-CLM)<1，(δLM-CLM)>1，0<(δLM-CLM)(δML-CML)<1，则从两个坐标全大于零的任意初始点出发的解，利用相平面分析可知，两条直线将相平面分成了四个区域，不论轨线从哪个区域的任一点出发，当t→+∞时:

证明

令

对P4进行分析，要使得平衡点有意义，即平衡点必须位于相平面的第一象限(坐标值为正值)，需要满足以下两个条件之一：

①(δLM-CLM)>1，0<(δML-CML)<1，(δLM-CLM)(δML-CML)>1；

②0<(δLM-CLM)<1，(δML-CML)>1，0<(δLM-CLM)(δML-CML)<1。

以下将分别讨论这两种情况：

1)对于(δLM-CLM)>1，0<(δML-CML)<1，(δLM-CLM)(δML-CML)>1情况，其相轨线如图1所示。

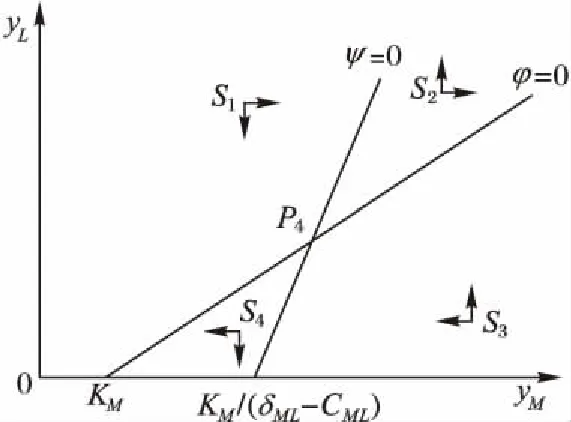
图1　平衡点稳定性的相平面(条件①)Fig. 1　Phase plane of equilibrium stability (condition ①)

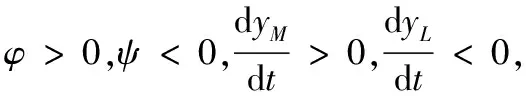
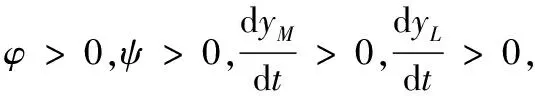
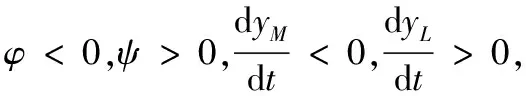
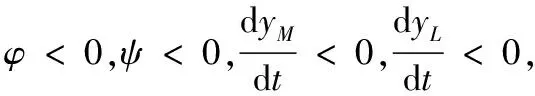
综上，系统并没有出现稳定性的均衡点，因此，此条件不满足，略去。

2)对于0<(δLM-CLM)<1，(δML-CML)>1，0<(δLM-CLM)(δML-CML)<1的情况，相轨线如图2所示。

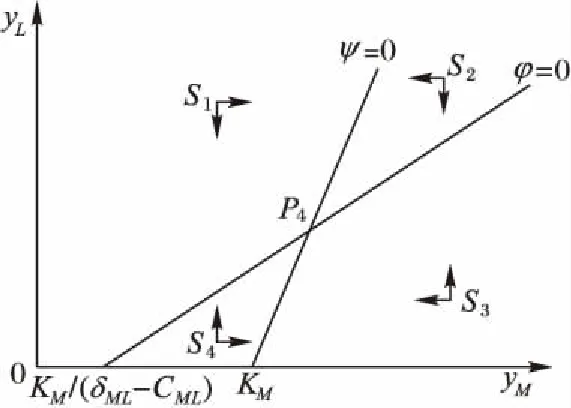
图2　平衡点稳定性的相平面图(条件②)Fig. 2　Phase plane of equilibrium stability (condition ②)

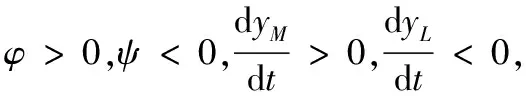
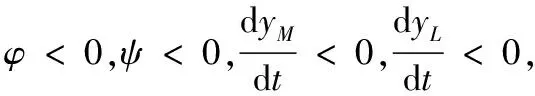
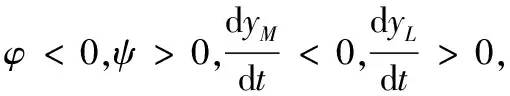
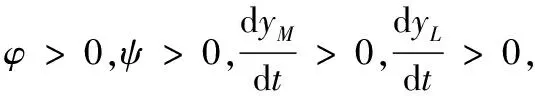
从而，系统最终演化方向为P4，原定理得证。

制造企业与物流企业达成联动发展要求满足0<(δLM-CLM)<1，(δML-CML)>1及0<(δLM-CLM)(δML-CML)<1，其中三个条件均大于零，表明制造企业与物流企业对彼此的贡献系数均大于竞争系数，δLM-CLM表示物流企业对制造企业的综合影响程度，δML-CML表示制造企业对物流企业的综合影响程度。而0<(δLM-CLM)<1，(δML-CML)>1表示物流企业对制造企业的综合影响程度小于制造企业对物流企业的综合影响程度，说明制造企业在其中规模较大，数量较少，占据主导地位，而物流企业数量众多，规模较小，多数提供相似服务，具有竞争性。同时，0<(δLM-CLM)(δML-CML)<1表示制造企业与物流企业对彼此的综合影响也相互牵制着，若提高物流企业对制造企业的综合影响值，则制造企业对物流企业的综合影响上限也会跟着提高，即彼此之间相应影响相互牵制。而综合影响值的大小在本质上主要受制于竞争系数和贡献系数的大小，以下将进一步分析平衡点稳定解的影响因素。

3　平衡点稳定解影响因素分析

3.1　竞争系数CLM、CML对平衡点稳定解的影响

令rM=rL=0.05，KM=1 000，KL=800，δLM=0.2，δML=3，CML=0.1，CLM分别取[0.1，0.15]区间的数，运用Matlab对式(7)和(8)进行编程运行后发现，随着物流企业对制造企业竞争系数的增加，制造企业与物流企业的产出水平均有所下降，但物流企业的产出水平下降得更为明显，如图3所示。其现实解释在于物流企业承担制造企业的部分外包业务，但如果物流企业自身的服务水平不提高的话将增加制造企业的运作成本，降低制造企业的产出水平，随着时间的演化，制造企业有可能把该业务外包给其他企业，从而导致该物流企业面临着订单萎缩的风险。

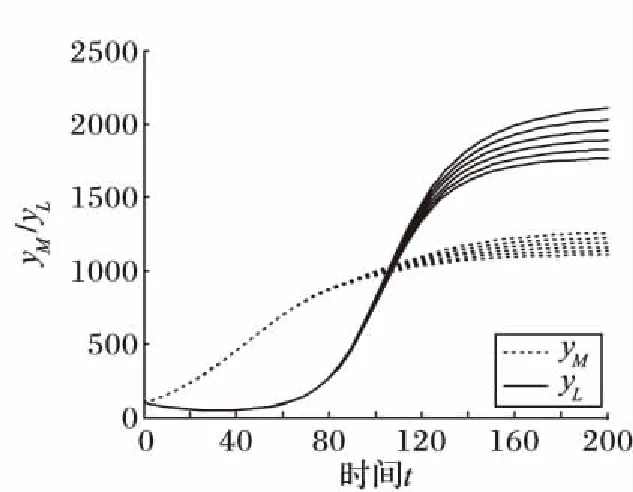
图3　竞争系数CLM对平衡点稳定解的影响路径Fig. 3　Influence path of competition coefficient CLM on stability of the equilibrium

令rM=rL=0.05，KM=1 000，KL=800，δLM=0.2，δML=3，CLM=0.1，CML分别取[0.1，0.6]区间的数，则可发现，随着制造企业对物流企业竞争系数的增加，制造企业与物流企业的产出水平均有所下降，但物流企业的产出水平下降得更为明显，如图4所示。其现实解释在于当制造企业选择自营物流的模式将对物流企业构成竞争关系，但对制造企业自身也未必有益，双方的产出水平均有所下降，但物流企业受到的影响更大，主要是因为其市场规模较小。因此，从长远来看，将物流外包始终是社会发展的一大趋势，当前要提高物流外包的比例。

在不考虑制造企业与物流企业对彼此的竞争系数的情况，将其运行结果与式(3)和(4)的运行结果进行比较后发现，制造企业与物流企业的产出水平的演化趋势如图5所示。随着时间的演化，在同一时刻，图5所对应的制造企业的产出水平和物流企业的产出水平均明显地高于图4，其中图5物流企业的产出水平更是明显地高于图4，进一步说明竞争系数的存在确实明显地影响到企业的发展，无论是制造企业还是物流企业都应该正视竞争对企业发展所带来的影响：对于物流企业来说，要化竞争压力为动力，创新物流服务模式，以争取到制造企业更多的物流订单量；对于制造企业来说，要通过物流外包的模式，实现主辅分离，保持企业核心竞争力。

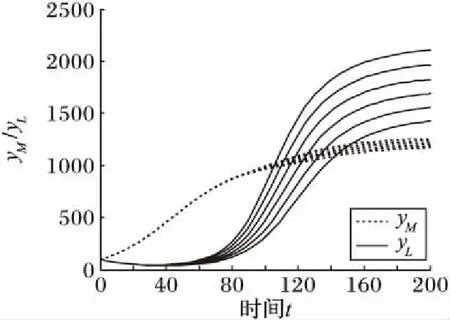
图4　竞争系数CML对平衡点稳定解的影响路径Fig. 4　Influence path of competition coefficient CML on stability of the equilibrium

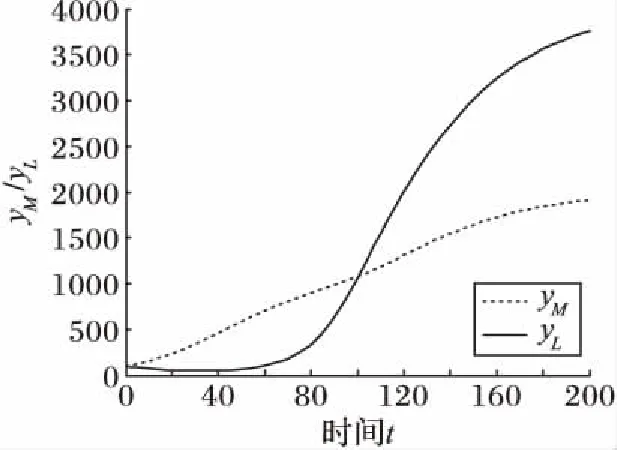
图5　不考虑竞争系数时制造企业与物流企业的产出水平演化趋势Fig. 5　Evolution trends of output level of manufacturing and logistics enterprises without considering competition coefficients

3.2　贡献系数δLM、δML对平衡点稳定解的影响

令rM=rL=0.05，KM=1 000，KL=800，CLM=CML=0.1，δLM=0.2，δML分别取[3，3.5]区间的数，则可以得到随着制造企业对物流企业的贡献系数的提高，双方的产出水平均有所提升，但物流企业产出水平的增长幅度明显地快于制造企业产出水平的增长幅度，如图6所示。其现实解释在于当制造企业选择物流外包的模式，将促使物流企业不断地提高自身的服务水平，创新物流服务模式，更好地满足制造企业发展的需要，因制造企业的规模较大，而物流企业规模较小，制造企业订单的一部分可能就占了物流企业绝大部分的订单，所以物流企业的产出水平变化幅度更大。

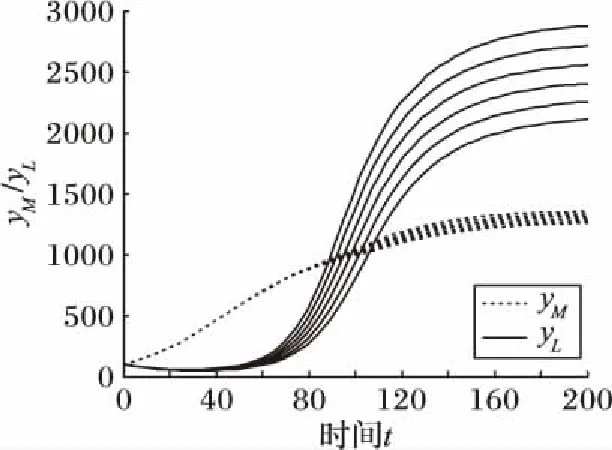
图6　贡献系数δML对平衡点稳定解的影响路径Fig. 6　Influence path of contribution coefficient δML on stability of the equilibrium

令rM=rL=0.05，KM=1 000，KL=800，CLM=CML=0.1，δML=3，δLM分别取[0.2，0.25]区间的数，则可以得到随着物流企业对制造企业的贡献系数的提高，双方的产出水平均有所增加，但物流企业产出水平的增长幅度明显地快于制造企业产出水平的增长幅度，如图7所示。其现实解释在于当物流企业提高自身的服务能力，将促进制造企业物流运作成本的降低，提高制造企业的产出水平，同时自身的收益也会增加，因制造企业的规模较大，而物流企业规模较小，制造企业订单的一部分可能就占了物流企业绝大部分的订单，所以物流企业的产出水平变化幅度更大。

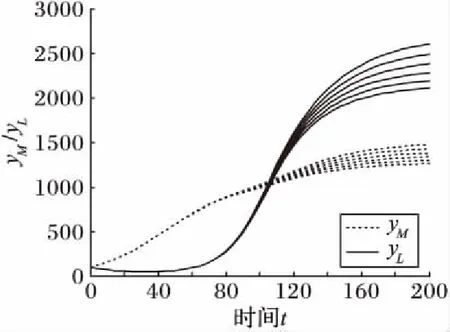
图7　贡献系数δLM对平衡点稳定解的影响路径Fig. 7　Influence path of contribution coefficient δLM on stability of the equilibrium

在不考虑制造企业与物流企业对彼此的贡献系数的情况下，将其运行结果与式(5)和(6)的运行结果相比较可知，制造企业和物流企业的产出水平图8相比较图6和图7均有大幅度下降，其中物流企业受到的影响尤其大，这也从另外一个方面说明了制造企业发展对物流企业的重要性。

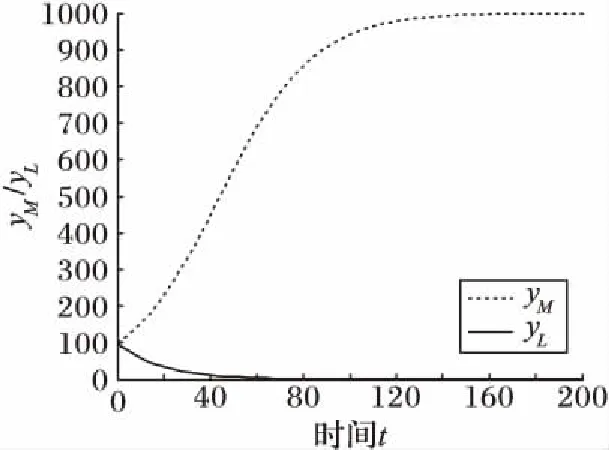
图8　不考虑贡献系数时制造企业与物流企业的产出水平演化趋势Fig. 8　Evolution trends of output level of manufacturing and logistics enterprises without considering contribution coefficients

3.3　环境容量KM、KL对平衡点稳定解的影响

令rM=rL=0.05，KL=800，CLM=CML=0.1，δLM=0.2，δML=3，KM分别取[800，1 500]区间的值，则可以得到随着制造企业环境容量的增加，制造企业的产出水平有较大幅度地增加，但物流企业产出水平变化不太明显，如图9所示。

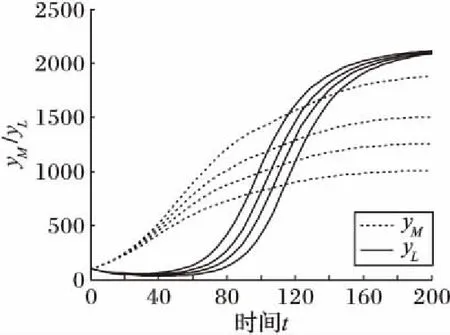
图9　环境容量KM对平衡点稳定解的影响路径Fig. 9　Influence path of environmental capacity KM on stability of the equilibrium

分别取rM=rL=0.05，KM=1 000，CLM=CML=0.1，δLM=0.2，δML=3，KL分别取[800，1 500]区间的值，则可以得到随着物流企业环境容量的增加，物流企业的产出水平有较大幅度地增加，但制造企业的产出水平则没有太大的变化，如图10所示。其现实解释在于在其他因素给定的情况下，双方之间的产出水平主要是受到其环境容量的影响，因此，一方的环境容量增加时对另外一方并没有太明显的影响。

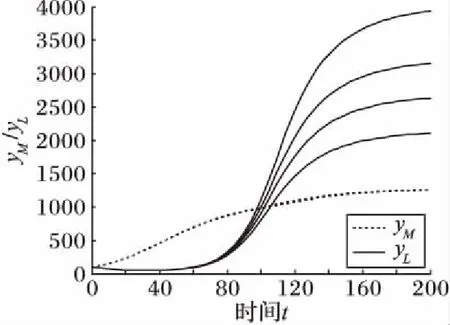
图10　环境容量KL对平衡点稳定解的影响路径Fig. 10　Influence path of environmental capacity KL on stability of the equilibrium

3.4　斜率变化对平衡点稳定解的影响

以上三点主要是从单个因素变化的角度来分析其对平衡点稳定解的影响，但事实上这些要素本身也是相互关联的。为了判定制造企业与物流企业产出之间的关系，可以分别取不同的斜率分析制造企业产出与物流企业产出之间的关系[21]，结合φ(yM,yL)=0及ψ(yM,yL)=0的表达式，可将其分别转化为如式(9)和(10)：

(9)

(10)

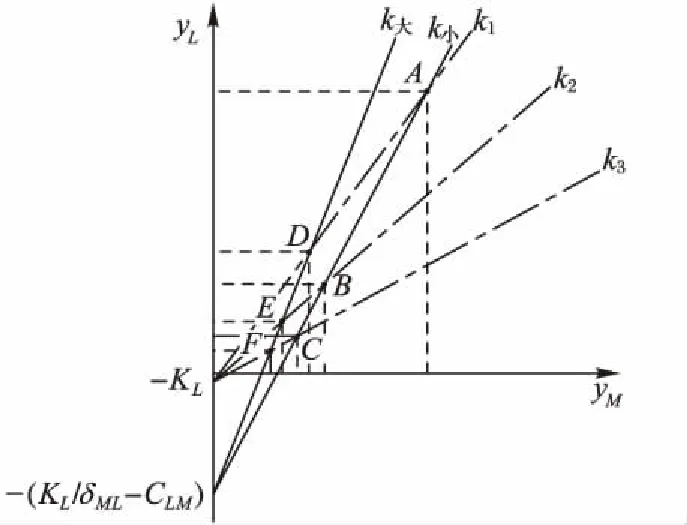
图11　斜率变化对平衡点稳定解的影响的相平面图分析Fig. 11　Analysis on phase plane of slope change to stability of equilibrium

当式(10)取较小的斜率(此处用k小表示)时，其与式(9)在不同斜率下(此处斜率值分别用k1、k2、k3表示，假设k1>k2>k3)分别相交于三点A、B、C；当式(10)取较大的斜率(此处用k大表示)时，其与式(9)在不同斜率下(此处斜率值分别用k1、k2、k3表示，假设k1>k2>k3)分别相交于D、E、F。

当斜率取k1时，假设k1=2/3，物流企业在点A处因制造企业变动一个单位所带来的产出量的增加小于在点D处因制造企业变动一个单位所带来的产出量的增加，点A和点D纵坐标的变化情况大于横坐标的变化程度，即ΔyL>ΔyM，物流企业在联动发展中的波动程度较为明显，因此，物流企业可以依托互联网+、科技创新等不断地提升自身的服务能力，更好地满足制造企业发展的需求，为自身创造更多的收益。

当斜率取k2，此处假定k2=0.5时，物流企业在点B和点E处纵坐标的变化情况正好等于横坐标的变化情况，即ΔyL=ΔyM，说明斜率的变化对双方的影响程度一样。

当斜率取k3，此处假定k3=1/3时，物流企业在点C和点F处纵坐标的变化情况小于横坐标的变化情况，即ΔyL<ΔyM，说明斜率的变化对制造企业的影响较大，制造企业在这里处于核心位置，外围的物流企业为其提供各式各样的物流服务，制造企业要积极营造竞争态势，敦促外围制造企业不断地提升服务能力，这样对制造企业来说也能在竞争合作中获得更多的利益。

4　案例应用与分析

A公司是全球最大的消费日用品生产商之一，20世纪90年代初从美国市场进入中国市场，为了使产品能够迅速抢占市场迫切需要强大的物流作为支撑，其对服务的响应时间、服务质量都提出了较高的要求。而B公司是国内最早运用现代物流理念的第三方物流企业，主要经营策划、物流运作管理、物流信息管理等物流一体化服务。

随后，A公司致力于在中国市场上寻找合适的承运铁路货运段的物流服务提供商，由于B公司广泛采用具有国际先进水准的标准作业程序(Standard Operating Procedure，SOP)和良好生产规范(Good Manufacturing Practice，GMP)而获得了与A公司签订三年运输合同的机会。A公司将其90%以上的订单交给B公司，可以说，A公司是B公司发展过程中非常关键的一个大客户，A公司对B公司的发展的贡献程度极其大，B公司几乎是依托于A公司而存在，在与A公司合作的过程中，A公司不断提出一些新的标准和要求，B公司为了适应A公司的物流服务需求，依托信息化水平建立了遍布全国范围的物流运作网络，也在一定程度上促使了B公司专业化服务水平的提升;当然，B公司的专业化服务水平也大大降低了A公司的市场运作成本，使得A公司可以迅速抢占市场先机。可以说，双方之间的合作极大地促进了彼此业务量的增长。

随着A公司生产规模的不断扩大，单纯一家B公司已经无法满足其物流需求，同时在这过程中B公司也出现了破损率上升、到货时间不及时等问题，为了进一步完善市场竞争机制，A公司也开始选择其他的物流服务提供商，给B公司施加一定的压力，B公司主要给A公司提供仓储服务，而其他的陆运服务、海运服务、配送服务等则交给其他的物流服务商。B公司承担了A公司将近60%的订单量，相比较于之前90%的订单量来说，此阶段的B公司所承担的A公司的订单量下降到将近60%。为了扩大业务量，B公司采取了以下措施：1)针对A公司的物流服务需求，建立了遍布全国的物流网络，为A公司提供全过程的增值服务，以更好地满足A公司发展的需要；2)B公司积极转变理念，正视A公司已逐步将部分物流业务外包的情况，努力寻找其他制造企业开展合作，如联合利华、安利、飞利浦、LG等，进一步降低对A公司的依赖程度；3)B公司通过各种各样的信息技术手段构建更为完善的物流信息系统，如电子数据交换、企业资源计划、企业对企业间电子商务活动平台、仓储管理系统、全球定位系统、无线射频识别等，进一步提升与其他企业进行谈判时的议价能力。

制造企业与物流企业要实现联动发展在很大程度上受制于双方能从联动发展中真正获得的利益的多少，具体来说与双方对彼此的贡献系数和竞争系数有很大的关系。对于制造企业与物流企业来说，竞争并不一定有害，关键的是要化竞争压力为动力，从本质上提升自身的服务能力。制造企业要充分认识到发展第三方物流是大势所趋，能够缩短订单周期、提高客户响应能力、降低物流成本，因此要实施制造业主辅分离，主动将物流环节交由第三方来运作，形成一批管理科学的物流一体化企业。物流企业要改变当前多、散、乱的状况，依托互联网+、科技创新等为其他企业提供更加精细化的物流服务，要加强物流企业与物流企业之间的战略联盟，提高自身的议价能力，有所分工，有所侧重，大力发展智慧物流，提升物流企业智能化水平，构建全方位供应链一体化服务体系。

5　结语

本文针对制造企业与物流企业联动发展过程中的竞争合作关系进行研究，主要在传统Logistic模型的基础上同时考虑贡献因子和竞争因子，提出了一个改进的Logistic-Volterra模型，解决了已有研究中存在的未充分考虑竞争关系的问题。本文首先系统梳理了制造企业与物流企业合作竞争研究中的相关模型，在此基础上构建了Logistic-Volterra模型；然后探讨了两业联动发展系统实现均衡的稳定性解以及达到稳定性解的数学条件和现实解释，同时运用Matlab数值模拟检验制造企业与物流企业形成稳定系统构成条件的影响因素；最后以A和B公司为例，分析了两家企业在联动发展过程中的竞合之路。

参考文献:

[1]中华人民共和国国务院.国办发〔2017〕73号:国务院办公厅关于进一步推进物流降本增效促进实体经济发展的意见[Z].北京,2017- 08- 30. (State Council Gazette of the People’s Republic of China. The general office of the State Council issued 2017 No. 73: Further reducing the logistics cost and promoting the efficiency of logistics to improve the development of real economy [Z]. Beijing, 2017- 08- 30.)

[2]GIRI B C, SARKER B R. Improving performance by coordinating a supply chain with third party logistics outsourcing under production disruption [J]. Computer & Industrial Engineering, 2017, 103: 168-177.

[3]ZHU W, NG S C H, WANG Z, et al. The role of outsourcing management process in improving the effectiveness of logistics outsourcing [J]. International Journal of Production Economics, 2017, 188: 29-40.

[4]中国物流与采购联合会.中国物流发展报告(2014—2015)[M].北京:中国财富出版社,2015:23. (China Federation of Logistics & Purchasing. China Logistics Development Report (2014—2015) [M]. Beijing: China Wealth Press, 2015: 23.)

[5]蒋志方,许振宇.MVC方法在制造车间物流系统仿真中的应用[J].计算机应用,1998,18(8):35-37. (JIANG Z F, XU Z Y. Application of MVC method in the simulation of manufacturing workshop logistics system [J]. Journal of Computer Applications, 1998, 18(8): 35-37.)

[6]刘小群,马士华.物流外包信息支持系统的规划与设计[J].计算机应用,2006,26(2):478-481. (LIU X Q, MA S H. Planning and design of logistics outsourcing information support system [J]. Journal of Computer Applications, 2006, 26(2): 478-481.)

[7]COLLEDANI M，TOLIO T. Integrated analysis of quality and production logistics performance in asynchronous manufacturing lines [J]. IFAC Proceedings Volumes, 2008, 41(2): 8368-8374.

[8]CHENG Y-H, LEE F. Outsourcing reverse logistics of high-tech manufacturing firms by using a systematic decision-making approach: TFT-LCD sector in Taiwan [J]. Industrial Marketing Management, 2010, 39(7): 1111-1119.

[9]TRAPPEY C V, LIN G Y P, TRAPPEY A J C, et al. Deriving industrial logistics hub reference models for manufacturing based economics [J]. Expert Systems with Applications, 2011, 38(2): 1223-1232.

[10]COLOVIC G. 5-Analyze of the planning, layout and logistics in garment manufacturing [M]// Management of Technology Systems in Garment Industry. New Delhi: Woodhead Publishing India Pvt. Ltd., 2011: 106-152.

[11]LAI K-H, WONG C W Y, CHENG T C E. Ecological modernization of Chinese export manufacturing via green logistics management and its regional implications [J]. Technological Forecasting and Social Change, 2012, 78(4): 766-770.

[12]WILFRIED S, HENRIK G, MARKUS F. Evaluation of a configuration model for the design of adaptable logistics chains in the railway vehicle manufacturing industry [J]. IFAC Proceedings Volumes, 2013, 46(9): 81-86.

[13]JONRINALDI, ZHANG D Z. An integrated production and inventory model for a whole manufacturing supply chain involving reverse logistics with finite horizon period [J]. Omega, 2013, 41(3): 598-620.

[14]BONNEY M, JABER M Y. Deriving research agendas for manufacturing and logistics systems: a methodology [J]. International Journal of Production Economics, 2014, 157: 49-61.

[15]BOUZON M, GOVINDAN K, RODRIGUEZ C M T. Reducing the extraction of minerals: reverse logistics in the machinery manufacturing industry sector in Brazil using ISM approach [J]. Resource Policy, 2015, 46, Part 1: 27-36.

[16]AZADIAN F, MURAT A, CHINNAM R B. Integrated production and logistics planning: Contract manufacturing and choice of air/surface transportation [J]. European Journal of Operational Research, 2015, 247(1): 113-123.

[17]POUR M A, ZANARDINI M, BACCHETTI A, et al. Additive manufacturing impacts on productions and logistics systems [J]. IFAC-PapersOnLine, 2016, 49(12): 1679-1684.

[18]王珍珍，陈功玉.基于Logistic模型的制造业与物流业联动发展模式研究[J].中国管理科学,2009,17(Special Issue):642-647. (WANG Z Z, CHEN G Y. Analysis on the interactive development modes of manufacturing and logistics industry based on Logistic model [J]. Chinese Journal of Management Science, 2009, 17(Special Issue): 642-647.)

[19]徐荣辉.逻辑斯蒂方程及其应用[J].山西财经大学学报,2010,32(2):311-322. (XU R H. Application of the Logistic equation [J]. Journal of Shanxi University of Finance and Economics,2010,32(2):311-322.)

[20]姜启源.数学模型[M].北京:高等教育出版社,2005:86-90. (JIANG Q Y. Mathematical Models [M]. Beijing: Higher Education Press, 2005: 86-90.)

[21]卓翔芝,王旭,王振锋.基于Volterra模型的供应链联盟伙伴企业合作竞争关系研究[J].管理工程学报,2010,24(1):132-137. (ZHUO X Z, WANG X, WANG Z F. Research on cooperative competition of supply chain alliance partners based on Volterra model [J]. Journal of Industrial Engineering and Engineering Management, 2010, 24(1): 132-137.)