基于改进Camshift的穿墙雷达运动人体目标成像跟踪算法

李松林，贾　勇，郭　勇，钟晓玲，崔国龙

(1.成都理工大学 信息科学与技术学院，成都 610059；　2.电子科技大学 电子工程学院，成都 611731)(*通信作者电子邮箱jiayong_cdut@hotmail.com)

0　引言

建筑物内运动人体跟踪是目前穿墙雷达领域的研究热点之一[1-3]，目前穿墙雷达运动人体跟踪的实现方法主要有：基于单发双收阵列的检测定位跟踪方法[4-5]和基于多输入多输出(Multi-Input Multi-Output，MIMO)阵列的目标成像跟踪方法[6-7]。由于MIMO阵列成像技术具有高信噪比、高分辨、抗干扰能力强等优点，逐渐成为目前建筑物内运动人体跟踪的主要方法。

阵列天线布局方式、未知墙体穿透补偿、多径杂波抑制、旁瓣栅瓣抑制均属于基于MIMO阵列的目标成像跟踪的研究热点。如文献[8]给出了适用于超宽带穿墙雷达运动人体成像跟踪的最优MIMO阵列布局；文献[9]提出了利用墙体回波信息推算反射系数、进而确定墙体参数以实现墙体穿透补偿的算法，形成了较高分辨率的运动目标图像；文献[10]推导出了在MIMO穿墙雷达成像中多径幻像的分布特性，并评估了相位相干因子(Phase Coherence Factor，PCF)对多径幻像抑制的性能；文献[11]在建立的多径模型基础上提出了从原始数据中消除多径回波的方法，在超宽带穿墙雷达成像中达到了实验预期效果；文献[12]利用MIMO多通道回波在目标区域和栅瓣区域相位分布的差异性，引入符号相干因子(Sign Coherence Factor，SCF)对穿墙雷达图像栅瓣进行抑制。上述研究均通过直接观察雷达图像的方式来判断运动目标的位置，然而墙体补偿误差、多径杂波和旁瓣栅瓣抑制残余，会造成单帧穿墙雷达图像中出现散焦、偏移、幻像甚至丢失的问题，从而使连续多帧雷达图像中目标图像呈现“闪烁”和“抖动”的特点；同时，空间分辨率和人体散射特性的变化会进一步加剧目标图像的“闪烁”和“抖动”，此时仍采用直接观察图像确定目标位置的方式，会对运动目标进行跟踪的可靠性和准确度造成影响。因此如何从穿墙雷达图像中提取目标位置并形成跟踪航迹也成为MIMO成像跟踪的一个研究方向，如文献[8]在修正的Kirchhoff目标成像算法的基础上对目标位置进行提取，形成了目标跟踪航迹，但并没有针对穿墙雷达图像给出具体的提取目标位置的方法。

本文针对MIMO穿墙雷达图像中运动目标位置提取与跟踪的需求，借鉴计算机视觉中的Camshift视频目标跟踪算法[13]，在建立的穿墙雷达图像颜色概率分布图中，首先采用目标预测的方法在概率分布图中确定目标存在可能性较大的搜索区域，从而滤除杂波、幻像等干扰；然后利用迭代的思想在目标搜索区域进行运动目标位置提取，减少了目标图像形状、大小变化对位置提取的影响；最后对提取的目标位置进行平滑滤波处理，得到连续稳定的跟踪航迹。实验结果表明，相比Meanshift与传统的Camshift跟踪算法，改进后的Camshift算法在MIMO穿墙雷达实时成像系统中对建筑物内运动人体目标具有更好的跟踪效果。

1　穿墙雷达运动人体目标成像跟踪模型

如图1所示的MIMO阵列运动人体目标成像跟踪模型，墙体后运动人体目标沿A、B、C运动到D点，假设MIMO天线阵列连续发送和接收n个周期超宽带脉冲信号，接收到n个周期的回波信号经两脉冲背景对消[14]、墙体补偿[15]和后向投影成像算法[16-17]得到n帧连续的穿墙雷达图像。

在连续的n帧穿墙雷达图像中，由于受穿墙雷达中多径杂波[18-19]、背景杂波残余[18-19]和图像旁瓣[20]及栅瓣[12]的影响，会在部分帧图像中出现幻像干扰；同时因为墙体补偿误差、图像分辨率变化以及运动人体目标散射特性变化，在多帧图像中会出现目标图像形状、大小变化，这些都会将影响目标位置提取的准确度。

图1　MIMO阵列运动人体目标成像跟踪模型Fig. 1　Moving target imaging tracking model based on MIMO array

2　本文算法

Camshift算法，即连续自适应Meanshift算法，其基本思想是对视频序列的所有图像作Meanshift运算，利用目标的颜色直方图模型将图像转化为颜色概率分布图，初始化一个搜索窗的大小和位置，并根据上一帧得到的结果自适应调整窗口的位置和大小[13]。利用这一优点，并结合穿墙雷达图像的特点，本文提出了基于改进Camshift的穿墙雷达运动人体目标成像跟踪算法，其关键是在每一帧穿墙雷达图像中准确提取目标位置，然后结合多帧目标位置信息给出跟踪滤波处理后的连续稳定的目标运动航迹。算法主要分为目标位置预测、目标位置提取及航迹平滑处理。

改进Camshift的穿墙雷达运动人体目标成像跟踪算法的处理流程如图2所示，相比传统的Camshift视频目标跟踪算法，改进后的算法对穿墙雷达成像图中目标位置提取进行了两点优化：第一，针对多径杂波、背景杂波残余、图像旁瓣和栅瓣的影响，本文在算法中融入目标预测思想，首先根据目标运动特征确定目标位置搜索波门(目标可能性较大区域)，抑制了波门外的幻像干扰。第二，由于墙体补偿误差散焦、图像分辨率变化、运动人体散射特性变化造成的目标图像形状、大小变化，将影响目标位置的提取。针对该问题，本文提出了目标图像质心位置迭代搜索，根据目标图像形状、大小变化，调整搜索窗尺度进行波门内目标质心位置迭代，提取出多帧目标位置信息，最后利用α-β滤波得到连续稳定的目标运动航迹。

图2　基于改进Camshift的穿墙雷达运动人体目标成像跟踪算法流程Fig. 2　Flow chart of moving target tracking algorithm based on improved Camshift for through-wall-radar imaging

2.1　颜色概率分布图

本文对目标位置的提取是在颜色概率分布图上进行的，颜色概率分布图中的像素概率值是用来度量目标出现“可能性”的值，这种可能性是目标运动过程中在此像素位置的概率。将MIMO阵列实时成像中得到的n帧连续穿墙雷达图像经直方图反向投影处理后得到颜色概率分布图[13,21]。在直方图反向投影的过程中，穿墙雷达图像中的像素被颜色直方图中相应的像素统计量所代替，然后重新量化就得到颜色概率分布图，定义如下：

假设像素种类为m个，像素个数共有j个，那么位置{(xi,yi)}i=1,2,…, j处直方图表示为{q}u=1,2,…,m，即在u=1,2,…,m出现的概率，定义一个映射c:R2→{1,2,…,m}，用以表示(xi,yi)的索引值，则直方图可以写成：

(1)

其中δ(x)是Delta函数,如下所示：

(2)

进行直方图归一化处理，即将[0,max(qu)]的范围变换到[0,255]。

(3)

其中:max[qu]是特征值中的最大值，m为特征空间中特征值的个数。设与原图尺寸相同的颜色概率分布图为I，(xi,yi)为原图像直方图中任意一像素点，则该像素点对应的颜色概率分布图的概率为pI(xi,yi):

(4)

2.2　目标跟踪起始

本文利用传统Camshift算法在前两帧穿墙雷达图像中进行目标起始速度确定。首先对前两帧图像进行直方图反向投影得到相应的颜色概率分布图，然后在第一帧图像中直接手动标注目标位置，以此确定下一帧固定的目标搜索波门，并在标注目标位置区域内建立目标图像颜色概率分布图；接着以当前帧目标位置为搜索中心，在固定的波门内进行第二帧目标位置搜索，该范围内某一区域像素概率值最大，即认定该区域为目标位置。利用得到的第一帧和第二帧的目标位置和时间关系，确定目标初始运动速度为：

(5)

其中时间T为连续两帧图像时间间隔。

2.3　目标位置预测

传统Camshift算法针对目标的大小，以n帧确定的目标位置直接作为第n+1帧目标波门搜索中心进行目标位置提取(计算像素概率值最大区域)。但是在MIMO雷达图像中，由于受多径杂波、背景杂波残余、图像旁瓣及栅瓣的影响，会造成图像散焦和幻像，图像中目标位置容易发生偏移，目标的航迹会受到很大影响，甚至会造成目标误判与错误航迹；同时目标处于运动状态，第n帧目标质心位置和第n+1帧目标质心位置会有一定距离，这使得部分帧图像出现虚假的目标位置以及目标跟踪丢失等问题。

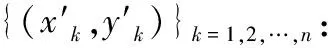
(6)

2.4　目标位置提取

在上文得到的目标可能性较大区域(即波门范围)内进行目标质心位置提取，然而在运动过程中，目标图像的形状、大小时刻在变化，目标图像的质心位置难以确定。针对这一问题，本节提出了目标质心位置迭代计算方法，在连续多帧雷达图像中，通过在波门范围内自适应调整目标搜索窗的大小，使搜索窗与目标图像相匹配，最后将搜索窗中心作为目标位置。

如图3所示，图中阴影部分为穿墙雷达图像中目标图像区域，虚线圆形为搜索波门，实线框为目标搜索窗，在目标跟踪起始之后，即第三帧开始，在波门范围内，以波门中心为当前时刻搜索窗中心(点S)，在上一帧搜索窗大小的基础上膨胀ρ倍作为当前时刻搜索窗大小，在此搜索窗内建立颜色概率分布图，利用其零阶矩和一阶矩来确定搜索窗内目标图像的质心位置。

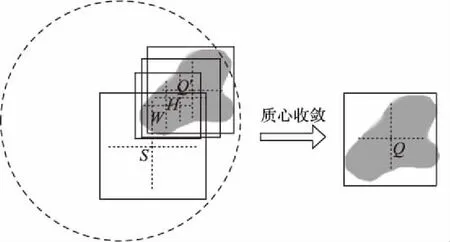
图3　提取目标质心位置过程Fig. 3　Process of extracting target centroid position

考虑到对噪声不敏感的突出优点，颜色概率分布图的零阶矩和一阶矩被用来确定搜索窗内目标图像的质心位置，零阶矩和一阶矩[13]分别定义为：

零阶矩：

(7)

X轴和Y轴方向一阶矩：

(8)

其中：pI(x,y)为颜色概率分布图中坐标(x,y)处的像素概率值，x和y的变化范围为当前搜索窗口的大小。

根据式(7)、(8)可得到目标图像区域的质心位置为：

(9)

每完成一次迭代计算，即确定了搜索窗内部分目标图像质心位置，然后将搜索窗中心移至该质心位置，并利用式(10)重新计算搜索窗大小。重复上述迭代过程，当搜索窗中心与波门范围内目标图像质心位置重合或距离小于设定的阈值，则认定迭代收敛。如图3所示，从点S到点Q′，其中W和H两点为迭代过程中搜索窗的中心位置，每一次迭代都会重新得到新的搜索窗中心位置。为了表述清晰，只选取了迭代过程中较典型的W和H两点，省略了迭代过程中其他搜素窗中心位置，此时将搜索窗中心作为当前帧提取的目标位置。

(10)

其中γ为搜索窗控制参数，根据大量的实测实验得出，当γ为2.5时，可实现搜索窗对目标图像的最优匹配。

在上述迭代过程中：膨胀系数ρ过大将增加波门范围内杂波幻像对目标图像质心位置提取的影响；ρ过小将降低迭代效率，甚至出现搜索窗未包含目标图像的情况，从而导致迭代中断。在本文给出的实验中设置ρ=1。

(11)

(12)

针对多帧连续雷达图像进行上述目标位置预测、目标位置提取，并得到每一帧滤波处理后的目标位置，最后形成连续稳定的目标运动航迹。

3　实验结果与分析

实验场景如图4所示，墙体为粘土砖墙，墙体厚度为0.24 m。穿墙雷达采用两发八收阵列，两个发射天线分别放置在接收阵列的两端，相邻收发天线间距为15 cm，相邻接收天线间距为30 cm。发射信号为步进扫频连续波(Stepped Frequency Continuous Wave, SFCW)信号，频带为1～2 GHz，频率步进为2 MHz。雷达设置在距墙体5 m处，并且距离地面1.2 m，以使聚焦平面在高度为1.75 m的人体散射部分(胸部位置)，即保证来自胸部位置散射的最强回波是形成人体图像的大部分数据。在建筑物内运动人体以不大于1.5 m/s的运动速度从一端墙角A位置(2,9)到达另一端B位置(-1,11)，如图4(a)所示。为了更好地说明本文算法的性能，图中标注了运动目标的实际运动航迹，并在下文对运动航迹进行了定量误差分析。

在本次穿墙雷达探测实验中，本文提取了100帧连续雷达图像对提出的算法进行验证分析，其中连续两帧图像间隔 为0.5 s。图5(a)～(c)分别给出了Meanshift算法、传统Camshift算法以及改进后Camshift算法对100帧连续雷达图像的跟踪结果。本文定义了均方根误差(Root-Mean-Square Error, RMSE)来定量分析改进Camshift算法与其他两种算法的跟踪航迹误差。

(13)

其中：n为图像帧数，实测实验中n=100；Xest,i为算法跟踪过程中第i帧目标位置；Xact,i为目标实际运动中的位置。

通过上述定义的均方根误差分析，改进Camshift算法与实际目标运动航迹相比均方根误差为0.272 m，传统Camshift算法和Meanshift算法均方误差分别为0.461 m、0.478 m，改进Camshift算法较传统Camshift算法跟踪航迹误差降低了40.99%，较Meanshift算法跟踪航迹误差降低了43.09%。整体上看，相比Meanshift算法和传统Camshift算法，本文提出的改进Camshift算法获得的目标航迹更加贴近目标运动状态，且人体目标跟踪航迹更为稳定平滑。

为了进一步说明算法的优势，图6给出了在跟踪过程中第3、42、100帧目标位置提取结果，在此三帧雷达图像中目标图像存在明显的大小起伏，且受到杂波幻像与旁瓣栅瓣的干扰，这些因素降低了Meanshift算法和传统Camshift算法对目标位置提取的可靠性，如图6(a)和(b)所示，用于提取目标位置的搜索窗未能够准确地圈定目标图像。对比而言，图6(c)给出的改进Camshift算法处理结果显示，目标搜索窗准确圈定了雷达图像中目标图像，从而形成了更平滑的跟踪航迹。实测数据验证了本文提出的改进Camshift算法通过引入目标预测和迭代搜索思想，可有效对抗雷达图像“闪烁”和“抖动”，保证了对目标位置提取的可靠性。

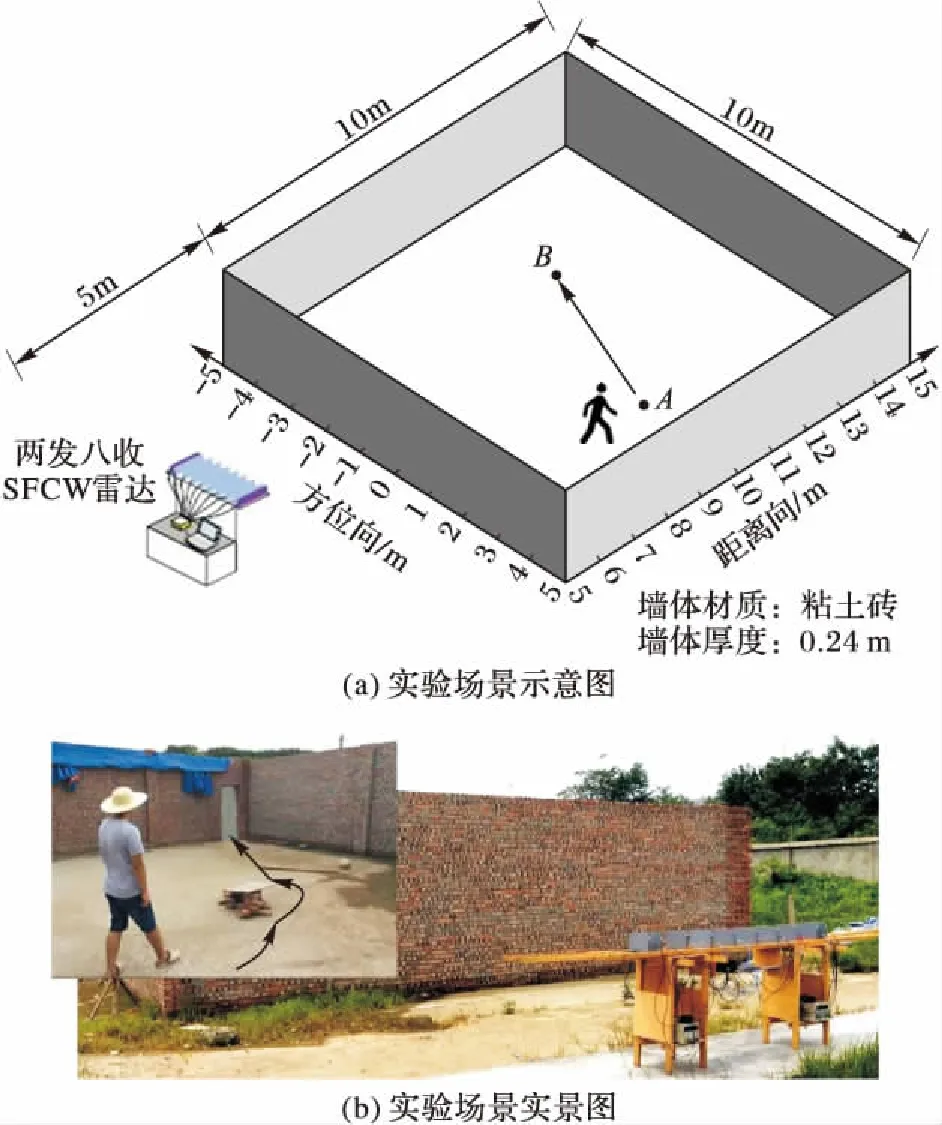
图4　实验场景Fig. 4　Experimental scene

4　结语

本文提出了基于改进Camshift的穿墙雷达运动人体目标成像跟踪算法，引入了目标预测与迭代搜索的思想，避免了连续多帧雷达图像的“闪烁”和“抖动”对目标位置提取的影响，最后由α-β滤波获得了连续稳定的目标跟踪航迹。实验结果表明：一方面相比直接观察图像的方式，本文算法获得的跟踪航迹清晰地给出了目标的运动过程；另一方面相比Meanshift与传统的Camshift算法，本文算法给出了平滑度更高的目标运动航迹。

图5　整体跟踪结果比较Fig. 5　Comparison of overall tracking results

图6　目标位置提取结果比较Fig. 6　Comparison of target position extraction results

参考文献:

[1]BEKTAS H O, OZDEMIR O, ORHAN M, et al. An experimental investigation of F-K migration and SAR algorithm using beam space MUSIC for UWB through-the-wall imaging [C]// Proceedings of the 2016 IEEE Radar Methods and Systems Workshop. Piscataway, NJ: IEEE, 2016: 70-75.

[2]HU J, SONG Y, JIN T, et al. Shadow effect mitigation in indication of moving human behind wall via MIMO TWIR [J]. IEEE Geoscience and Remote Sensing Letters, 2015, 12(3): 453-457.

[3]TIVIVE F H C, BOUZERDOUM A, AMIN M G. An SVD-based approach for mitigating wall reflections in through-the-wall radar imaging [C]// Proceedings of the 2011 IEEE Radar Conference. Piscataway, NJ: IEEE, 2011: 519-524.

[4]AHMAD F, AMIN M G. A noncoherent approach to radar localization through unknown walls [C]// Proceedings of the 2006 IEEE Radar Conference. Piscataway, NJ: IEEE, 2006, 4: 583-589.

[5]IYA N M, MUQAIBEL A H, JOHAR U M. Ultra wideband wall compensation for through-wall tracking and imaging [C]// ICUWB 2011: Proceedings of the 2011 IEEE International Conference on Ultra-wideband. Piscataway, NJ: IEEE, 2011: 81-85.

[6]WANG W, LU B, SONG Y, et al. Parallel realization of moving target imaging in 2D MIMO through-wall radar applications [C]// ICCP 2015: Proceedings of the 2015 International Conference on Communication Problem-Solving. Piscataway, NJ: IEEE, 2015: 137-140.

[7]RALSTON T S, CHARVAT G L, PEABODY J E. Real-time through-wall imaging using an ultrawideband Multiple-Input Multiple-Output (MIMO) phased array radar system [C]// ARRAY 2010: Proceedings of the 2010 International Symposium on Phased Array Systems and Technology. Piscataway, NJ: IEEE, 2010: 551-558.

[8]吴世有,谭恺,徐艳云,等.超宽带穿墙雷达天线阵列配置分析及运动人体跟踪成像算法[J].电子与信息学报,2012,34(11):2601-2607. (WU S Y, TAN K, XU Y Y, et al. Study on UWB through-wall radar antenna array configuration and moving person tracking and imaging algorithm [J]. Journal of Electronics & Information Technology, 2012, 34(11): 2601-2607.)

[9]AFTANAS M, SACHSY J, DRUTAROVSKY M, et al. Efficient and fast method of wall parameter estimation by using UWB radar system [J]. Frequenz, 2009, 63(11/12): 231-235.

[10]LIU J, KONG L, YANG X, et al. First-order multipath ghosts’ characteristics and suppression in MIMO through-wall imaging [J]. IEEE Geoscience and Remote Sensing Letters, 2016, 13(9): 1-5.

[11]CHEN X, CHEN W. Multipath ghost elimination for through-wall radar imaging [J]. IET Radar, Sonar & Navigation, 2015, 10(2): 299-310.

[12]LIU J, JIA Y, KONG L. Sign-coherence-factor-based suppression for grating lobes in through-wall radar imaging [J]. IEEE Geoscience & Remote Sensing Letters, 2016, 13(11): 1681-1685.

[13]BRADSKI G R. Computer vision face tracking for use in a perceptual user interface [J]. Intel Technology Journal, 1998, Q2: 214-219.

[14]WANG H-N, LU B-Y, ZHOU Z-M, et al. Through-the-wall imaging and correction based on the estimation of wall parameters [C]// Proceedings of the 2011 IEEE CIE International Conference on Radar. Piscataway, NJ: IEEE, 2011: 1327-1330.

[15]LIU J, KONG L, YANG X, et al. Refraction angle approximation algorithm for wall compensation in TWRI [J]. IEEE Geoscience & Remote Sensing Letters, 2016, 13(7): 943-946.

[16]DEHMOLLAIAN M, SARABANDI K. Refocusing through building walls using synthetic aperture radar [J]. IEEE Transactions on Geoscience & Remote Sensing, 2008, 46(6): 1589-1599.

[17]AHMAD F, AMIN M G, MANDAPATI G. Autofocusing of through the-wall radar imagery under unknown wall characteristics [J]. IEEE Transactions on Image Processing, 2007, 16(7): 1785-1795.

[18]TAN Q Y, LEUNG H, SONG Y, et al. Multipath ghost suppression for through-the-wall-radar [J]. IEEE Transactions on Aerospace and Electronic Systems, 2014, 50(3): 2284-2292.

[19]GENNARELLI G, SOLDOVIERI F. Multipath ghosts in radar imaging: physical insight and mitigation strategies [J]. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, 2014, 8(3): 1078-1086.

[20]WANG W, LU B, QIU L, et al. A modified adaptive sidelobe reduction method for through-the-wall radar imaging [J]. IEEE Geoscience and Remote Sensing Letters, 2016, 13(9): 1255-1259.

[21]XIU C, BA F. Target tracking based on the improved Camshift method [C]// CCDC 2016: Proceedings of the 2016 Chinese Control and Decision Conference. Piscataway, NJ: IEEE, 2016: 3600-3604.