基于密度峰值的混合型数据聚类算法设计
李 晔,陈奕延,张淑芬
(1.中国市场学会 服务质量专业委员会,北京 100048; 2.河北省数据科学与应用重点实验室(华北理工大学),河北 唐山 063210)(*通信作者电子邮箱townjam_sovietnia@163.com)
0 引言
随着互联网技术的迅速发展,人们采集与获取信息的能力大大提高。当海量信息出现时,人们希望从繁多复杂的数据中得到有价值的信息。聚类分析是数据挖掘中一个极其重要的分支。文献[1]指出聚类是一个把数据对象划分成子集的过程,每个子集是一个簇,使得簇中的对象彼此相似,但与其他簇中的对象不相似。
根据数据对象(数据点)每个属性值的数据类型,可把数据分为数值型数据、分类型数据(无序分类变量构成的数据)及混合型数据。很多科研工作者为保证数据分析的普适性和全面性,采用的调查数据大多为既含数值型属性又含分类型属性的混合型数据。由于面对的数据类型日益多样化,聚类分析也需要处理不同类型的数据,然而目前的聚类算法大多是针对数值型数据提出的,也有一部分可用来处理分类型数据,但能够处理混合型数据的聚类算法却相对较少。文献[2]指出这两种属性在属性值的取值范围、分布和特点上差异较大,许多研究人员认为针对单一属性数据的传统聚类算法已不适用于混合属性数据。因此,设计更多针对混合型数据的聚类算法是聚类分析中一项极具意义的工作。
最早用于混合型数据的聚类算法是k-prototypes算法[3],该算法结合了k-means和k-modes两种方法,故而不像很多传统的聚类算法一样只能处理单一属性的数据集。另外,该算法具备了k-means算法高效性的特点,应用十分广泛,尤其是对于大型数据集也十分有效。虽然k-prototypes算法有很多优点且被人们广泛使用,但仍存在以下一些不足:1)无法实现对数据分布的适应性。对于簇中的数值部分,k-prototypes算法同k-means算法一样只能发现球状分布的簇。2)无法自动确定簇的个数。3)没有考虑聚类过程中的模糊性问题。很多情况下,数据对象很可能同时分属多个簇,有时簇边界附近的数据对象的归属问题会很模糊,而k-prototypes算法并未考虑这一点。4)对混合属性数据簇原型(中心)的表示可能造成严重的信息丢失。5)没有考虑每个属性对聚类结果影响的差异性。6)受初始值的影响很大。由于k-prototypes算法是一种迭代算法,只能收敛于局部最优解,因此对初值的选取十分敏感。
近年来有不少研究者纷纷对上述缺点进行了不同程度的改进。针对缺点3):文献[4]在k-prototypes算法的基础上提出了fuzzyk-prototypes聚类算法,通过在k-prototypes算法中引入模糊理论的概念,增加了数据对象分配到簇原型时的不确定性,使改进的算法具有分析模糊性和不确定性问题的能力;文献[5]中则认为常用于混合型数据模糊聚类的fuzzyk-prototypes算法仅仅是在原始的模糊C均值(Fuzzy C-Means, FCM)聚类算法中使用了不同的相异性函数,从而使其可用于同时具有数值型属性和分类型属性的混合型数据,于是该文中提出了一个全新的FCM-type算法,采用全概率相异性函数来处理混合属性数据,通过交叉熵使得模糊目标函数正则化,最终达到提高聚类精度的目的。针对缺点4),文献[6]提出了fuzzyk-prototypes聚类算法的一种改进算法,该算法改进了簇原型的选取方式,对每个有p种不同取值的分类型属性,将其看成是一个p维的属性,迭代过程中原型的计算也要将每个分类型属性看成一个p维的属性,按每个分类型属性的可能取值在所属簇中的比例来定义簇原型,从而也间接改变了分类型属性的相异性度量方式。这样的原型选取方式包含了更多的数据信息,从而提高了聚类的精度。针对缺点5):文献[7]提出了基于聚类相似性的算法——SBAC算法,它是一个凝聚层次聚类算法,引入了一个相似度的度量方式来计算数据对象间的相似性;文献[8]提出了基于熵权法的针对混合属性数据的聚类算法,改进了数据对象之间距离的度量方式,利用信息熵作为各个属性的权值,从而提高了聚类的精度和稳定性;文献[9]中利用类内和类间信息熵来度量各个属性在聚类过程中的作用,由此给不同的属性分配不同的权重,从而使得数据对象可以在统一的框架下更客观地度量彼此之间以及对象与簇原型之间的相异性。针对缺点6),文献[10]对k-prototypes聚类算法初始点选取方法作了改进,通过对模糊k-prototypes的分析,分别对数值型属性部分和分类型属性部分进行划分,在每个划分中选取初值,最后将两部分和在一起组成初始的簇原型。该方法降低了数据对初值的敏感度,从而减少了聚类算法的迭代次数,同时还能避免选取到相同的初始簇原型。
虽然目前国内外针对缺点3)~6)有诸多改进,但却鲜有针对缺点1)和2)的改进算法,故本文主要针对这两个不足之处提出一种可用于混合型数据的新型聚类算法。2014年,文献[11]提出一种用于数值型数据的CFSFDP(Clustering by Fast Search and Find of Density Peaks)聚类算法,该算法具有能发现任意形状数据集且能自动确定簇数的优点,但使用范围局限于数值型数据。之后文献[12]进行了基于CFSFDP算法的模糊聚类研究;文献[13]提出了基于近邻距离曲线和类合并优化CFSFDP的聚类算法;文献[14]提出一种基于簇中心点自动选择策略的密度峰值聚类算法;文献[15]提出一种基于粒子群算法的CFSFDP算法。这些改进虽然提高了CFSFDP算法的性能,但仍然不能用于混合型数据的聚类。
因此,本文首先重新定义了混合型数据之间的距离,接着把CFSFDP算法扩展到混合型数据,这样可以克服k-prototypes算法相应的1)、2)两个缺点,使得该算法能够自动确定簇数,并且对于任意形状的簇都有一个比较满意的聚类效果。接着对算法复杂度进行分析,并且研究了算法中的阈值dc及权值γ的选取问题,分别利用数据场中的势熵和可度量数值型及分类型数据集聚类趋势的统计量来确定这两个参数。最后用文献[16]中的三个混合型数据集作为实验对象,通过和k-prototypes算法的比较来验证针对混合型数据的寻找密度峰值算法的有效性。
1 寻找密度峰值的聚类算法
本文把CFSFDP算法扩展到混合型数据,提出一种可用于混合型数据的寻找密度峰值聚类算法,该算法的基本思想是簇中心应该同时满足以下两点:1)簇中心的密度比它周围的点的密度更大;2)簇中心离比自身密度大的点的距离较远,即不同的簇中心之间的距离相对较远。
该想法是整个聚类过程的基础,找到簇中心以后,也就自动确定了簇的个数。对于任意一个非簇中心数据点i,认为点i跟所有比它密度更大的点中与之距离最近的那个点属于同一个簇。该算法中簇的分配在一步中完成,这与那些通过迭代来优化目标函数的算法是不同的。
1.1 相关定义

(1)
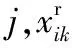
1.1.1计算ρi
计算密度时常用的核函数包括截断核(Cut-off kernel)、高斯核(Gaussian kernel)和指数核(Exponential kernel),它们的定义分别如下:
(2)
(3)
(4)
式(2)~(4)中的参数dc>0为阈值(截断距离),需由使用者事先指定。
1.1.2计算δi

ρq1≥ρq2≥…≥ρqN
(5)
然后定义
(6)
至此,对于S中的每个数据点xi,可利用式(2)、 (3)或(4)以及式(6)为其计算(ρi,δi)(i∈IS)。
根据ρi,δi的定义可知,当某个点的这两个量同时取值较大时,这个点就满足前文提到的成为簇中心的两个条件,因此可以利用以ρ为横轴,δ为纵轴的图(称为决策图)来判断哪些点同时具有较大的ρ值和δ值,即哪些点可以被当成是簇中心。
1.2 算法步骤及流程
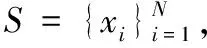
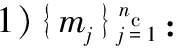
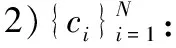
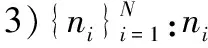
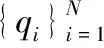
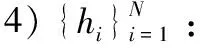
下面利用上述符号给出寻找密度峰值聚类算法的具体步骤。
步骤1初始化及预处理。
1)给定用于确定阈值(截断距离)dc的参数t∈(0,1)。
2)给定权值γ。
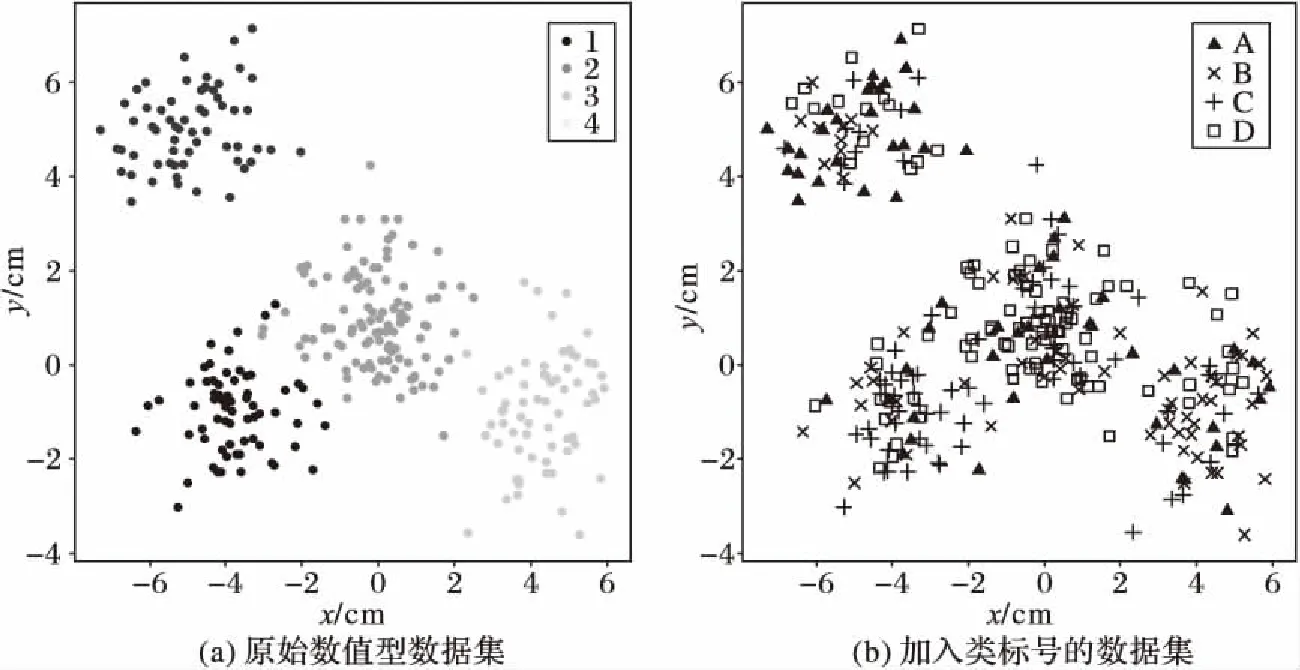
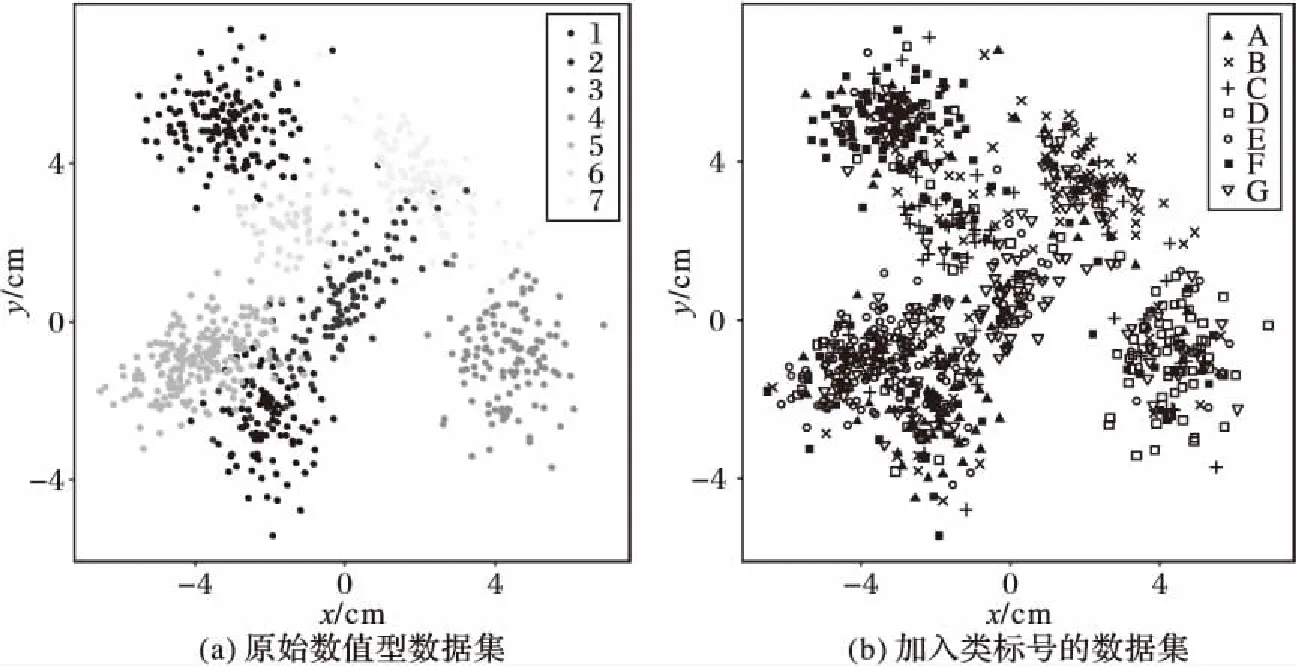
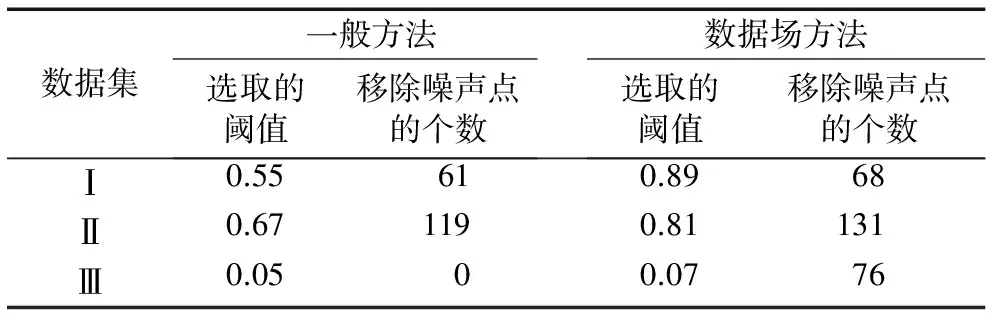
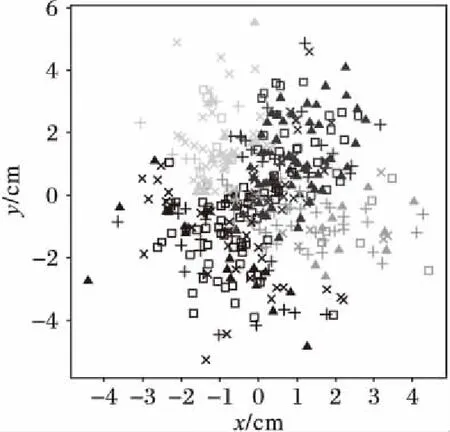
3)计算距离dij,并令dji=dij(i 4)确定阈值dc。 将上一步计算的距离dij(i 步骤3对非簇中心数据点进行归类。 注1:当处理某个xqi时,若所有比xqi密度大的点到xqi的距离都相等,则把xqi随机分配到一个xqj(j 步骤4若nc>1,则将每个簇中的数据点进一步分为“簇核心”和“簇光晕”。 1)初始化标记hi=0(i∈IS)。 2)确定每个簇的边界区域。这个区域中的数据点定义如下:它们属于该簇,且在与其距离不超过dc的范围内,存在属于其他簇的数据点。 在针对混合型数据的寻找密度峰值算法中,给定阈值dc及权值γ后,该算法的时间复杂度主要包括距离矩阵的计算,本文算法需计算n(n-1)/2个距离值,n是数据集中的数据对象数,因此算法时间复杂度为O(n2)。k-prototypes算法的时间复杂度为O((l+1)kn),其中k是簇数,n是数据集中的数据对象数,l是k-prototypes算法收敛所需的迭代次数。当n很大时,本文算法的时间复杂度可能会远高于k-prototypes算法。 从以上论述可知,新算法中可能影响最终聚类结果的因素主要有两个: 1)密度公式中的阈值(截断距离)dc;2)距离公式中的权值γ。接下来需进一步讨论并验证这两个因素对聚类结果的影响,并给出一个相对合理的方式来选取这两个参数,以达到最理想的聚类效果。 对于dc的选取,文献[11]给出了一种一般性的方法:选取一个dc,使每个数据点的平均“邻居”个数大约为数据点总数的1%~4%,这里的“邻居”是指与其距离不超过dc的点,具体的比例通常根据研究人员的经验和实际的数据集而定。 以上方法需要根据个人实际经验来确定dc,但通过下文的实验(这些实验的细节会在2.1.3节中介绍)可以看到,聚类结果会受到阈值dc的影响,而根据经验很难估计出最优的阈值dc。对同一数据集,若阈值的经验估计值不同,则聚类的结果可能也不同。 为了解决这一问题,使用数据场中的势熵从混合型数据集中自动提取最优的阈值dc。文献[17]提出用数据场去描述数据空间中对象之间共同的交互作用,同时文献[18-19]指出对于同样的参数,数据点在稠密区域有较高的势而在稀疏区域有较低的势。 可用于计算势的势函数有很多种,如高斯核、指数核、截断核等。接下来介绍如何通过数据场中的势熵计算出在不同势函数和不同数据集下的最优阈值。 2.1.1数据场 假设在数据空间Ω中有一个混合型数据集X={x1,x2, …,xn}。文献[19]指出受到物理上场论的影响,将X中的一个数据对象当成一个在给定的任务中传播它的数据分布的物理对象,这就形成了数据场。对于一个任意的点xi∈Ω(1=1,2,…,n),场函数按如下公式定义: (7) 其中:σ是一个影响因子;mj是xj的质量;K(x)是一个单位势函数,xi-xj是点i和另一个点j之间的方位距离。σ对最终的势分布有一定的影响。K(x)给出了数据对象把它的数据分布扩散到数据场中的规则,通常情况下K(x)选择为高斯核函数。 2.1.2利用数据场提取最优的截断距离 在式(7)中,如果数据场是一个标量场,则mj=1,当K(x)选择高斯核函数时,xi-xj变成dij,dij表示点xi和xj之间的某种距离,那么每一个点的势φi由如下公式计算: (8) 图1 原始数值型数据集和加入类标号的数据集ⅠFig. 1 Original numeric data set and data set with the class label Ⅰ 图2 原始数值型数据集和加入类标号的数据集ⅡFig. 2 Original numeric dataset and dataset with class label Ⅱ 如果式(8)中的dij和新算法中dij的度量方式相同,并且如果新算法在计算密度时也选取高斯核函数,那么点xi在数据场中的势φi和在新算法中的密度ρi是等价的,也就是说式(8)与式(3)是等价的。 同理,当数据场中的势函数和密度公式都取为截断核函数或指数核函数时,点xi在数据场中的势φi和在新算法中的密度ρi是也等价的。因此在寻找密度峰值的聚类算法中,阈值dc的最优化问题可以转化为数据场中影响因子σ的最优化问题。我们希望找到一个影响因子σ使得随机变量的不确定性达到最小。 在信息论与概率统计中,熵[20]是随机变量不确定性的度量,熵越大,随机变量的不确定性越大。 设X是一个取有限个值的离散随机变量,其概率分布为: P(X=xi)=pi;i=1,2,…,n (9) 则随机变量X的熵定义为: (10) 因此,可以使用熵来最优化σ。对于数据集X,如果数据场中每个点的势为{φ1,φ2,…,φn},则熵H的定义如式(11): (11) 由于取相同的核函数时,数据场中的影响因子σ与新算法中密度公式里的阈值dc等价,因此通过计算使熵H达到最小的影响因子σ,就可以得到寻找密度峰值聚类算法中的最优阈值dc。 2.1.3实验和分析 为了更加直观地看到选取不同阈值时的聚类结果,且为了验证基于数据场的方法提取最优阈值的合理性,本节使用具有两个数值型和一个分类型属性的混合型数据集进行模拟,数据的记录按照如下方法产生。 首先生成四组二维数据点。第一组包含四个正态分布并且包含300个点(如图1(a));第二组包含七个正态分布并且包含840个点(如图2(a));第三组是两个环状分布并且包含400个点(如图3(a))。然后给每个点加入一个分类值,从而把这些点扩展到3维,分别记这三个数据集为Ⅰ、Ⅱ和Ⅲ(如图1(b)、2(b)、3(b))(文献[21]展示了本文所有彩色原图)。 需要注意的是,一个点的分类值不能表明它是哪个类成员。事实上,这些点完全没有类,分类值仅仅代表对象在第三维既不是连续的也不是有序的。因此对每个数据集加入分类值时,我们使分类型属性可能的取值个数等于仅考虑数值型属性时二维平面中簇的个数,这样做是为了分别利用数值型属性和分类型属性进行聚类时簇的个数相等,把两个属性放在一起考虑时也可以有一个统一的聚类簇数(在此先不考虑数值型属性和分类型属性的权重问题),同时也可以在模拟实验中看到该算法自动选取的簇数是否合理。 对于第一个数据集,把每个正态分布看成一部分,并且给每部分的大多数点分配其中一个分类型属性值,使得拥有这个分类型属性值的点数与拥有其余的分类型属性值的点数大致相等。例如在图1(b)左上角的部分中大多数点被分配属性值A,并且这部分其余的点被分配属性值B、C或者D。所有的分配都是随机的。剩下两个数据集的分类值的分配情况类似(如图2(b)、3(b))。 对于同样的数据集选择相同类型的核函数和相同的距离公式,如果聚类结果不同,说明阈值dc对该聚类算法的聚类结果有重要的影响。在本实验中使用数据集Ⅰ,并且度量数据集中数据点的密度时选用高斯核函数。将数据集中所有对象之间的距离dij(i 图3 原始数值型数据集和加入类标号的数据集ⅢFig. 3 Original numeric dataset and dataset with class label Ⅲ 图4 数据集Ⅰ对于选取不同阈值的聚类结果Fig. 4 Clustering results with different thresholds for dataset Ⅰ 为了印证利用数据场得到阈值dc是一种较合理的方法,接下来仍继续使用数据集Ⅰ、Ⅱ和Ⅲ进行比较性模拟实验,实验中计算数据场中势的势函数和计算数据集中点密度的核函数均选取高斯核函数,距离度量公式中数值型和分类型属性的权值取为γ=2。对于利用经验选取阈值的方法,将所有的dij(i 由前述可知,寻找密度峰值的聚类算法可识别出数据集中的噪声点(异常值),噪声点会对聚类算法产生一定干扰,因此,须尽可能多地识别出噪声点从而提高算法的稳定性。表1中列出了利用两种不同方法选取阈值时,算法移除噪声点的个数。从表1可以看到,对于这三个数据集,利用数据场提取阈值的方法比利用经验的方法移除的噪声点更多。同时对于这三个数据集,无论是用一般性的方法选取阈值还是利用数据场自动提取阈值都与每个数据集对应的合理簇数一致(进行模拟的数据集包含的簇数),所以至少可以说明利用数据场来确定阈值的方法不会比利用经验来确定的方法表现更差,而且它对于任何的数据集都适用,也就是说对于任意的数据集都可以自动计算出一个阈值,而不需要根据用户的经验来指定,因此该方法的适用性更广。 对于混合型数据的聚类,距离公式中分类型属性权值γ的选取也会直接影响到最终的聚类效果,通常为了简单起见,可以取γ=1,即两种属性的权重相等。文献[3]指出混合型数据距离公式中权值γ的选取依赖于数值型属性的分布,即权值γ的选取依赖于数值型属性的平均标准差σ,但该文献并未给出具体应如何选取以及这样选取的依据。因此本节对权值γ的选取提出一个新的方法。 表1 利用两种不同方法选取阈值时移除噪声点的个数Tab. 1 Number of removed noise points with different threshold selected by two different methods 2.2.1聚类趋势 对于给定的数据集,几乎每个聚类算法都可以为该数据集返回簇,然而如果数据集中根本不存在自然的簇,那么通过聚类算法所产生的簇很可能不具有实际的意义。考虑一个完全随机结构的数据集,如数据空间中均匀分布的点,尽管聚类算法仍然可以人工地把这些点划分成簇,但这些簇是随机的,不具有任何意义。所以只有当数据集有明显的聚类趋势时,聚类算法返回的簇才有实际意义。 因此,可以提出这样的方法来确定权值γ:1)分别计算混合型数据集中数据对象的数值部分和分类部分的聚类趋势。数值部分的聚类趋势可以利用霍普金斯(Hopkins)统计量的变化形式来计算,分类部分的聚类趋势利用下文2.2.3节中提出的统计量来计算。2)如果数值部分的聚类趋势更明显,那么希望γ小一些;如果分类部分的聚类趋势更明显,那么希望γ大一些。 2.2.2数值型数据集的聚类趋势 对于给定的混合型数据集,将其中的数值部分取出构成一个数值型数据集,然后将该数据集与其在数据空间中的均匀分布进行比较,以此评估该混合型数据集中数值部分的聚类趋势。霍普金斯统计量可用来度量数值型数据集的聚类趋势。 霍普金斯统计量[1]是一种空间统计量,检验空间分布的变量的空间随机性。给定混合型数据集D,取出其中的数值型部分组成一个数值型数据集Dr,它可以看作随机变量Z的一个样本,想要确定Z在多大程度上不同于数据空间中的均匀分布,可以根据文献[1]中总结的步骤来计算: (12) (13) 3)计算可度量数值型数据集聚类趋势的统计量Hr(霍普金斯统计量的变形)。 (14) 2.2.3分类型数据集的聚类趋势 受到可度量数值型数据集聚类趋势的霍普金斯统计量的启发,对于分类型数据集,同样可以提出一个用来度量其聚类趋势的统计量Hc。 Hc是一个可以评估分类型数据分布随机性的统计量。给定混合型数据集D,取出其中的分类型部分组成一个分类型数据集Dc,然后按以下步骤计算: (15) (16) 3)计算可度量分类型数据集聚类趋势的统计量Hc: (17) 2.2.4权值γ的计算 从以上分析可以看到,Hr越小说明混合型数据中数值部分的聚类趋势越明显;同理,Hc越小说明混合型数据中分类部分的聚类趋势越明显。因此,如果混合型数据集D的Hr越小,则希望γ的取值越小,即希望聚类时更多的考虑数值型属性;相反,如果混合型数据集D的Hc越小,则希望γ的取值越大,即希望聚类时更多地考虑分类型属性。因此可以按以下公式定义权值γ: γ=Hr/Hc (18) 2.2.5实验与分析 为了更加直观地看到选取不同权值时的聚类结果并且验证利用聚类趋势定义权值的合理性,使用一个新的仅有三个属性的混合型数据集Ⅳ进行模拟,属性中有两个数值型和一个分类型,这些数据记录按如下的方式产生。 首先生成一组二维数据点,这组数据包含400个点且是一个正态分布(图5(a));然后通过给每个点加入一个分类值把这些点扩展到三维(图5(b))。对于这个数据集我们人为地把它分成四个部分:用以(0,0)为坐标原点的坐标轴把区域分成左上、左下、右上、右下,因此给每部分中的大多数点分配一个分类值,使得拥有这个分类值的点数与拥有其余分类值的点数大致相等。举个例子,在图5(b)中右上角的部分大多数点被分配属性值A并且这部分其余的点被分配B、C或者D。 模拟的主要目的是验证在该算法中数值型和分类型属性如何相互影响,如果只考虑数值型属性,那么可知这个二维数据只包含一个自然簇;当加入第三维分类型属性时,可知那些空间上离得比较近且有相同分类值的点更倾向于分到同一个簇。图6为数据集Ⅳ对于不同权值γ的聚类结果,其他的参数完全一样,其中不同的颜色表示聚类后得到的不同的簇。从图6可以看到,对于不同的权值γ,聚类结果的差异很大,所以对权值选取的讨论很有必要。当权值很小(γ=0.1)时,分类型属性的贡献较小,虽然难以解释此时的聚类结果,但可以看到空间上离得比较近的点会被分到同一个簇;随着权值γ的增加,可以看到第三维上类标号相同的点会逐渐被分到同一个簇中。对于数据集Ⅳ,当权值γ=7.5时,所有类标号相同的点被分到同一个簇。 图5 原始数值型数据集和加入类标号的数据集ⅣFig. 5 Original numeric dataset and the dataset with class label Ⅳ 接下来对数据集Ⅳ使用本文提出的方法计算一个较为合理的γ。利用式(18)得到γ=0.37,聚类结果见图7,其中不同的颜色表示聚类后得到的不同的簇。从图7可以看到,γ=0.37时的聚类结果与之前人为的划分较为吻合,大致分成左上、左下、右上、右下四个部分,因此也从另一个角度说明了γ选取的合理性。 为了进一步对提出的寻找密度峰值聚类算法进行验证,本章使用一些实际数据集进行测试,并对实验结果进行分析。 为了验证本文算法的有效性,选用UCI机器学习库[16]中的Cylinder Bands(以下简称Cylinder)、German Credit Data(以下简称German)和Postoperative Patient Data(以下简称Patient)这三组混合型数据集,数据描述见表2。分别在这三组数据集上对新算法和原始的k-prototypes算法进行测试,聚类结果的分析主要依靠聚类的准确率。 为了比较不同算法的正确率,引用文献[22]提出的聚类正确率定义,算法在数据集上的聚类正确率如下: (19) 其中:k为该数据集真实的类的个数,corr_ci表示第i个类中被正确聚类的样本个数,|D|为该数据集的样本个数。 由此看出,ac_rate值越大,聚类效果越好。当聚类结果与已知类标号完全一致时,取得最大值1。 图6 数据集Ⅳ对于不同的权值的聚类结果Fig. 6 Clustering results of different weights in dataset Ⅳ 图7 数据集Ⅳ的一个合理权值的聚类结果Fig. 7 Clustering result of reasonable weight of the dataset Ⅳ 表2 实际数据集描述Tab. 2 Real dataset description 对于k-prototypes算法,使用式(1)作为数据对象之间的相异性度量,γ取为1(使得数值型属性和分类型属性有同等的地位)。对于新提出的算法,按照常规参数选取和本文新提出的参数选取分别进行验证,这样不仅可以测试新型算法的有效性,同时可以测试新提出的参数选取方法的有效性。对于新型算法的常规参数选取,γ取为1,阈值dc取为所有的dij(i 表3 不同算法的聚类正确率比较Tab. 3 Comparison of clustering accuracy of different algorithms 本文打破了对混合型数据进行聚类时最常用的k-prototypes算法的框架,把用于数值型数据的CFSFDP算法扩展到混合型数据,提出了一种新的针对混合型数据的寻找密度峰值聚类算法。该算法不像k-prototypes算法一样仅仅考虑对象到簇中心(原型)的距离,而是考虑了对象之间的某种关系,认为密度高的点“控制”了与它距离最近的低密度点,这样可以使那些距离较远但原本属于同一个自然簇的对象在聚类过程中能被正确地分配,由此实现了该算法对簇分布的适应性,而不像k-prototypes算法那样只能识别球状分布的簇。同时该算法在确定簇中心的同时也就自动确定了簇的个数,而不需要像k-prototypes算法根据经验事先指定簇数。 虽然本文提出的针对混合型数据的聚类算法在很多情况下是很有效的,但仍存在一些不足之处,通过算法复杂度分析可以看出寻找密度峰值聚类算法的时间复杂度较高,当采用本文提出的方法选取阈值和权值时会进一步增加其复杂度,因此对于超大型数据集,其有效性还需进一步验证,在未来的研究中需要针对该算法的复杂度问题作更深入的讨论。 参考文献: [1]HAN J W, KAMBER M, PEI J. 数据挖掘:概念与技术[M].范明,孟小峰,译.3版.北京:机械工业出版社,2012:288,315-316. (HAN J W, KAMBER M, PEI J. Data Mining: Concept and Techniques [M]. FAN M, MENG X F, translated. 3rd ed. Beijing: China Machine Press, 2012: 288, 315-316.) [2]冀进朝.针对多维混合属性数据的聚类算法研究[D].长春:吉林大学,2013:I. (JI J C. Research on clustering algorithms for the data with multidimensional mixed attributes [D]. Changchun: Jilin University, 2013: I.) [3]HUANG Z. Clustering large data sets with mixed numeric and categorical values [C]// PAKDD 1997: Proceedings of the First Pacific-Asia Knowledge Discovery and Data Mining Conference. Singapore: World Scientific, 1997: 21-34. [4]CHEN N, CHEN A, ZHOU L. Fuzzyk-prototypes algorithm for clustering mixed numeric and categorical valued data [J]. Journal of Software, 2001, 12(8): 1107-1119. [5]CHATZIS S P. A fuzzyc-mean-types algorithm for clustering of data with mixed numeric and categorical attributes employing a probabilistic dissimilarity functional [J]. Expert Systems with Application, 2011, 38(7): 8684-8689. [6]王宇,杨莉.模糊k-prototypes聚类算法的一种改进算法[J].大连理工大学学报,2003,43(6):849-852. (WANG Y, YANG L. An improved algorithm for fuzzyk-prototypes algorithm [J]. Journal of Dalian University of Technology, 2003, 43(6): 849-852.) [7]LI C, BISWAS G. Unsupervised learning with mixed numeric and nominal data [J]. IEEE Transactions on Knowledge and Data Engineering, 2002, 14(4): 673-690. [8]孙浩军,高玉龙,闪光辉,等.基于熵权法的混合属性聚类算法[J].汕头大学学报(自然科学版),2013,28(4):58-65. (SUN H J, GAO Y L, SHAN G H, et al. A clustering algorithm based on entropy weight for mixed numeric and categorical data [J]. Journal of Shantou University (Natural Science), 2013, 28(4): 58-65.) [9]赵兴旺,梁吉业.一种基于信息熵的混合型数据属性加权聚类算法[J].计算机研究与发展,2016,53(5):1018-1028. (ZHAO X W, LIANG J Y. An attribute weighted clustering algorithm for mixed data based on information entropy [J]. Journal of Computer Research and Development, 2013, 53(5): 1018-1028.) [10]周才英,黄龙军.模糊K-Prototype聚类算法初始点选取方法的改进[J].计算机科学,2010,37(7A):69-75. (ZHOU C Y, HUANG L J. Improvement of the method to choosing the initial value of fuzzyK-prototypes clustering algorithm [J]. Computer Science, 2010, 37(7A): 69-75.) [11]RODRIGUEZ A, LAIO A. Clustering by fast search and find of density peak [J]. Science, 2014, 344(6191): 1492-1496. [12]BIE R, MEHMOOD R, RUAN S, et al. Adaptive fuzzy clustering by fast search and find of density peaks [J]. Personal and Ubiquitous Computing, 2016, 20(5): 785-793. [13]蒋礼青,张明新,郑金龙,等.快速搜索与发现密度峰值聚类算法的优化研究[J].计算机应用研究,2016,33(11):3251-3254. (JIANG L Q, ZHANG M X, ZHENG J L, et al. Optimization of clustering by fast search and find of density peaks [J]. Application Research of Computers, 2016, 33(11): 3251-3254.) [14]马春来,单洪,马涛.一种基于簇中心点自动选择策略的密度峰值聚类算法[J].计算机科学,2016,43(7):255-258,280. (MA C L, SHAN H, MA T. Improved density peaks based clustering algorithm with strategy choosing center automatically [J]. Computer Science, 2016, 43(7): 225-258, 280.) [15]詹春霞,王荣波,黄孝喜,等.基于改进CFSFDP算法的文本聚类方法及其应用[J].数据分析与知识发现,2017,1(4):94-99. (ZHAN C X, WANG R B, HUANG X X, et al. Application of text clustering method based on improved CFSFDP algorithm [J]. Data Analysis and Knowledge Discovery, 2017, 1(4): 94-99.) [16]UCI database [EB/OL]. [2017- 01- 20]. http:// archive.ics.uci.edu/ml/datasets.html. [17]WANG S, GAN W, LI D, et al. Data field for hierarchical clustering [J]. International Journal of Data Warehousing and Mining, 2011, 7(4): 43-63. [18]WANG S, CHEN Y. HASTA: a hierarchical-grid clustering algorithm with data field [J]. International Journal of Data Warehousing and Mining, 2014, 10(2): 39-54. [19]WANG S, WANG D, LI C, et al. Clustering by fast search and find of density peaks with data field [J]. Chinese Journal of Electronics, 2016, 25(3): 397-402. [20]李航.统计学习方法 [M].北京:清华大学出版社,2012:60. (LI H. Method of Statistical Learning [M]. Beijing: Qinghua University Press, 2012: 60.) [21]陈奕延.《基于密度峰值的混合型数据聚类算法设计》——聚类效果彩色图[EB/OL]. [2017- 09- 09]. http://blog.csdn.net/dr_chenyiyan/article/details/77914036. (CHEN Y Y. Design of hybrid data clustering algorithm based on density peak: Chromatic effect diagrams in clustering [EB/OL]. [2017- 09- 09]. http://blog.csdn.net/dr_chenyiyan/article/details/77914036.) [22]AL-SHAMMARY D, KHILI I, TARI Z, et al. Fractal self-similarity measurements based clustering technique for SOAP Web messages [J]. Journal of Parallel and Distributed Computing, 2013, 73(5): 664-676.
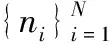
1.3 算法复杂度分析
2 阈值和权值的选取
2.1 阈值dc的选取



2.2 权值γ的选取


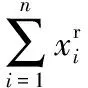
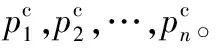

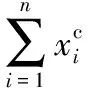

3 实证分析
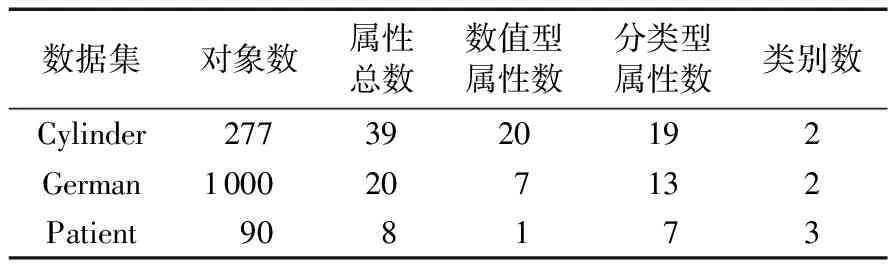
3.1 数据集的选取
3.2 评价指标
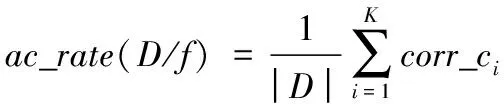

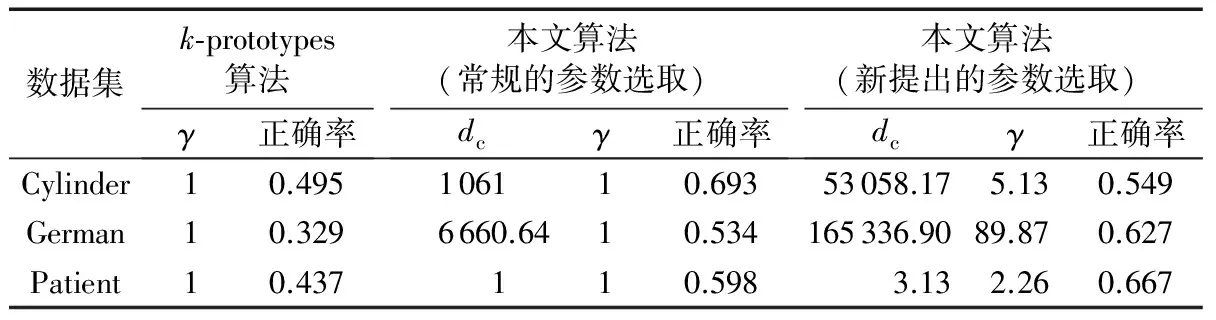
3.3 实验结果
4 结语

