大规模标签图中的动态Top-K兴趣子图查询
宋宝燕,贾春杰,单晓欢,丁琳琳,丁兴艳
(辽宁大学 信息学院,沈阳 110036)(*通信作者电子邮箱shanxiaohuan@lnu.edu.cn)
0 引言
图因独有的结构化特征而广泛用于描述生物技术[1]、军事管理等领域的复杂网络关系,而网络中数据类型的多样化则可通过具有节点特征标识能力的标签图表示。子图查询[2]是图数据处理的基本问题,即在数据图中搜索同构于查询图的所有匹配子图。
随着信息技术的飞速发展,上述领域的数据爆炸式地增长且动态变化,大量信息中用户往往只对若干匹配结果感兴趣,同时希望通过增加限制条件而减少信息过载的负面影响,因此将Top-K查询引入子图查询中。现有的Top-K子图查询方法多集中在中小规模静态图上,由于查询效率、存储开销等原因无法直接应用于大规模动态图;支持动态图子图查询的方法中,多数采用累积定时方式对图及索引进行更新,这将导致更新间隔内的查询结果因图的动态变化而存在一定误差;同时实际应用中存在一类具有重要意义的查询,以DBLP作者合作关系网为例,查询作者间合作密切(利用边权值大小表示)的具有特定结构的实力强劲的K个团队,然而现有方法鲜有支持此类用户个性化限定的兴趣子图查询。
鉴于上述问题,本文利用标签图节点、边独有的特征特性,提出了一种动态Top-K兴趣子图近似查询方法(Dynamic Top-KInteresting Subgraph Query,DISQtop-K)。本文主要工作如下:
1)提出一种图拓扑结构特性(Graph Topology Structure Feature, GTSF)索引,该索引由节点拓扑结构特性(Node Topology Feature Index, NTF)索引和边特性(Edge Feature, EF)索引构成。利用NTF索引可根据节点度、邻接点等信息过滤无效节点,以获得相对较小的候选节点集;利用EF索引可根据边的类型标签及权值快速过滤不满足权值限制的无效边,进而获得相对较小的候选边集。
2)提出基于GTSF索引的多因素候选集过滤策略,利用加权边、节点度以及邻接点频率等特征限制对查询图候选集进一步剪枝,以避免匹配验证阶段的冗余计算。
3)提出Top-K兴趣子图匹配验证方法,该方法考虑到图的动态变化可能对匹配结果产生影响,将匹配验证过程分为初始匹配和动态修正两个阶段,初始阶段在候选集上按照匹配顺序进行逐一匹配以获得初始结果集;动态修正阶段,利用图动态变化对初始结果集进行动态修正,尽可能保证查询结果的实时、准确。
4)基于真实数据集和模拟数据集,在存储空间及索引创建时间、查询效率等方面进行了大量实验,验证了本文方法的有效性。
1 相关工作
目前子图查询方法多采用过滤-验证的方式,根据过滤方式的不同可分为三类:无索引结构、频繁子图索引和可达性索引过滤。
无索引结构方法将直接进行匹配验证。Ullmann算法[3]是一种基于状态空间搜索的子图同构检测方法,主要通过细化过程来消除树搜索过程中的后继节点个数,从而达到剪枝的目的,以提高确定同构的效率。由于其使用的是递归的穷举方法,因此在小规模图上效率较高。VF2算法[4]对Ullmann进行了优化,通过使用一组可行性规则对搜索空间进行剪枝,增加了查询节点匹配顺序,但在大规模图上的查询效率极低。STwig算法[5]同样不使用图形索引,而是利用并行技术解决子图查询,然而连接操作将产生大量无用中间结果,以致空间复杂度和时间复杂度相对较高。TurboISO[6]提议合并查询图中的相似节点(具有相同标签并位于相同区域的顶点),并将查询图转化成一棵生成树,通过路径过滤法过滤掉不可行的候选节点。BoostIso[7]对TurboISO进行了优化,先将数据图中的相似节点进行合并,然后同样通过路径过滤法进一步减少不必要的中间结果。但TurboISO和BoostIso只适用于具有相似节点的查询图和数据图;同时,由于路径过滤运行时间会随着数据集的增加呈现指数增长,对于大规模查询图和数据图,TurboISO和BoostIso均无法高效处理子图查询问题。文献[8]提出了一个新框架,通过对查询图进行CFL(Core Forest Leaf)分解来消除不相似节点笛卡尔积的冗余问题;同时提出一种辅助数据结构索引CPI(Compact Path Index),不仅可以用于计算匹配顺序,还可以实现对数据图的剪枝,进而对数据图中的可能查询结果进行压缩编码。但是,该算法由于没有动态查询机制,在大规模动态标签图上查询效率较低。
频繁子图索引方法指的是找到频繁子图或经常查询的子图,并对这些频繁结构进行索引,避免了匹配过程中过多的连接操作。SUBDUE算法[9]是在单个图中挖掘频繁子图的经典算法;SpiderMine[10]则对其进行优化,旨在从图中挖掘前K个最大频繁模式。这两种子图查询方法只适用于具有频繁子图结构的数据图。
可达性索引方法则通过构建索引结构和一些优化策略对候选集进行裁剪,基于回溯的方式逐步列举解决方案并验证查询图节点所对应的候选集,从而递归地形成最终的查询结果。SPath[11]和GraphQL[12]都是利用每个节点的邻居进行过滤,使得候选节点数最小化。其中GraphQL利用广度优先搜索树的形式,进一步对候选节点进行过滤,从而迭代地进行查找;SPath则通过记录一些基本的路径实现对节点的过滤。由于SPath与GraphQL在过滤中记录了过多信息,造成了较多不必要的内存开销,同时这两种方法均没有涉及等价节点重复枚举和匹配顺序选择问题。
在实际应用中,人们往往关注兴趣度比较高的查询结果,因此引出更具针对性的Top-K子图查询问题。Top-K子图查询主要分为两个部分:一是根据查询图在数据图中找到所有的匹配子图;二是将所有的匹配子图根据兴趣度排名获得兴趣度最大的K个兴趣子图。目前Top-K子图查询主要分为两种模式:先匹配后排序模式和边匹配边排序模式。
先匹配后排序模式,即先获取所有匹配子图,然后根据兴趣度对所有的匹配子图排序,从而获得最优的K个匹配子图,如RAM算法[13],通过建立SPath索引结构对候选集进行过滤,然后匹配验证获得所有匹配子图,根据兴趣度对所有的匹配子图排序,从而获得最优的K个匹配,由于获取所有匹配结果的过程相对较复杂,因此在大规模图上的Top-K子图查询效率较低。边匹配边排序模式则在匹配验证的过程中过滤掉兴趣度明显较小的匹配子图,如RWM[14]针对RAM进行改进,采用边匹配边排序的模式,提出两种索引结构对候选集进行剪枝,查询效率相对提高,然而由于其Top-K匹配的顺序随机,因此将产生大量的冗余计算。
综上分析可知,目前对于Top-K子图查询算法大多存在两个问题:一是大多数算法仅解决无权查询图的匹配问题,没有考虑用户的个性化需求,即没有涉及加权查询图的匹配处理;二是在实际应用中,图会随着时间推移、实际应用语义的改变而发生拓扑结构的变化,动态图下的Top-K子图查询研究相对较少。
2 动态Top-K兴趣子图近似查询
2.1 问题描述
2.1.1图标签
本文讨论的无向加权标签图可通过(V,E,L,W)四元组形式表示,其中:V为节点集合;E为边集合;L为节点标签集合;L(v)为节点v的标签值,用以表示节点的某种特征;W则为边权值集合。
以DBLP作者合作关系网为例,网络中作者、研究领域关键字以及学术会议均抽象为图中节点,如图1所示,用标签A、K、C表示,即利用图标签表示节点的不同种类,边则表示三者之间的关系,边权值用以表示作者间合作关系以及作者参与会议的程度、关键字间相似程度等。
2.1.2兴趣子图
在现实生活中,根据查询需求的不同,人们往往对具有某种结构的查询图感兴趣,并且希望通过限定查询图中某些节点间的特殊关系而实现更精准的查询。例如,在由军人和其擅长的技术组成的军事网络中,要组建一个4人团队完成某项任务,其中要求2人枪法精准,1人擅长英语和计算机,1人仅擅长英语,且枪法精准的2人曾有过多次合作,即可将该查询问题抽象为查询具有上述结构且节点间权值具有一定限制的子图,通常将此类子图称为兴趣子图。本文将针对此类兴趣子图查询问题展开深入研究。
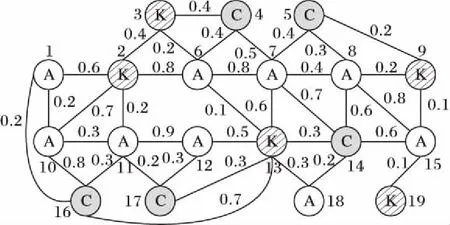
图1 数据图GFig. 1 Data graph G
2.1.3动态Top-K近似查询
兴趣子图查询将根据用户查询需求,从数据图中搜索与查询图结构相同、边权值满足某种限制且联系紧密的所有子图。在实际应用中,常通过标签图中边权值大小来标识两个实体的关联程度,各个实体间的关联程度则反映整个网络的紧密程度,本文将用图的兴趣度来表示,其规范化定义如下:
定义1兴趣度。若M是查询图Q在数据图G中的一个匹配子图,则组成M的所有边的权值之和即为该匹配子图的兴趣度,表示为I(M)。
如图2所示,P1、P2是查询图Q的两个匹配子图,它们的兴趣度分别为:I((P1)= 2.1,I(P2)= 2.3。
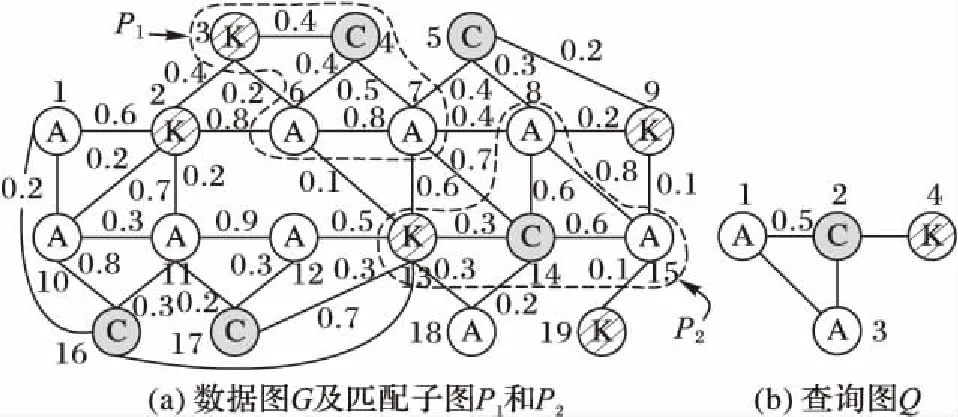
图2 查询Q的两个匹配子图P1与P2Fig. 2 Two matched subgraph P1 and P2 of query Q
随着图数据规模的日益增大,Top-K查询因可有效解决信息过载带来的巨大开销而得到广泛应用。大规模图的Top-K兴趣子图查询,即搜索同构于查询图的K个最大兴趣度的子图。实际应用中,网络常随时间推移、实际应用语义的改变而发生拓扑结构的变化,即数据图发生节点或边的插入、删除等,如何保证大规模动态图下Top-K兴趣子图查询的高效性面临严峻挑战。研究发现,当前动态图数据处理常采用定时累积更新取代实时更新,以减少频繁I/O造成的巨大通信开销,这将导致更新间隔内的查询结果存在一定的误差,然而图动态变化是一个长期且稳定的过程,一段时间内的变化量远小于图数据规模,对子图查询结果影响相对较小,因此,本文将针对大规模动态图中的Top-K兴趣子图近似查询展开研究。本文方法处理过程主要由索引建立、候选集过滤以及子图匹配验证三个阶段构成。
2.2 图拓扑结构特性索引
子图同构匹配本身是一个NP完全问题,随着数据图及查询规模的扩大,算法的搜索效率会大幅度下降,现有方法多采用过滤-验证策略,通过提取图节点信息或某些子结构信息建立具有过滤能力的索引以提高查询效率。为此本文结合标签图的自身特性,利用图节点及边信息,提出一种图拓扑结构特性索引(GTSF索引),该索引由节点拓扑结构特性索引(NTF索引)和边特性索引(EF索引)构成。
2.2.1NTF索引
研究发现,标签图中节点的度、类型标签和不同类型邻接点等属性具有标志性和可辨别性,因此本文利用该特性提出NTF索引,该索引由两级结构构成,顶层结构根据节点标签类型进行索引,底层结构则建立每种标签类型包含的节点拓扑关系,以达到高效过滤无效节点的目的。
NTF顶层索引项由〈节点标签类型,所属类型节点数〉构成,底层索引项则由〈节点编号,节点度,各类型邻接点个数〉组成,通过广度优先算法统计各个节点的标签类型、度、邻接点类型及个数等拓扑结构特性。由于节点的度越大,它提供的信息量越大,在查询匹配时就可能更有价值,因此本文将索引项按照节点度进行降序排列。以图1为例,数据图G中包含A、K、C三种类型的节点,其NTF索引如图3所示。其中:id表示节点编号,degree表示节点的度,numA、numK和numC分别表示A、K、C三种类型节点的数量。
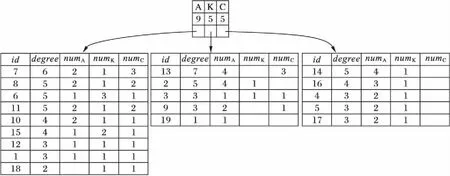
图3 NTF索引Fig. 3 Index of NTF
2.2.2EF索引
由标签图特性分析发现,除节点外,边同样蕴含大量信息,如边类型、权值等。为进一步过滤无效结构,本文提出了EF索引,该索引同样包含两级索引结构,顶层结构根据边标签类型(由两端节点类型组成)进行索引,底层结构则为每种边标签类型包含的边信息,通过EF索引可以快速获取各边的类型标签及权值。
EF顶层索引项由边类型构成,底层索引项则由〈边端点1,边端点2,权值〉三元组构成。由于Top-K兴趣子图查询目的是根据查询图Q在数据图G中查询K个兴趣度最高的匹配子图,而由兴趣度定义可知其随着边权值的增大而增大,因此为有效过滤不满足条件的边,本文将EF索引项按边权值进行降序排列。仍以图1为例,数据图G包含AA、AK、AC、CK和KK五种类型的边,其EF索引如图4所示,其中id1、id2表示边的两个节点的编号,w表示边的权值。
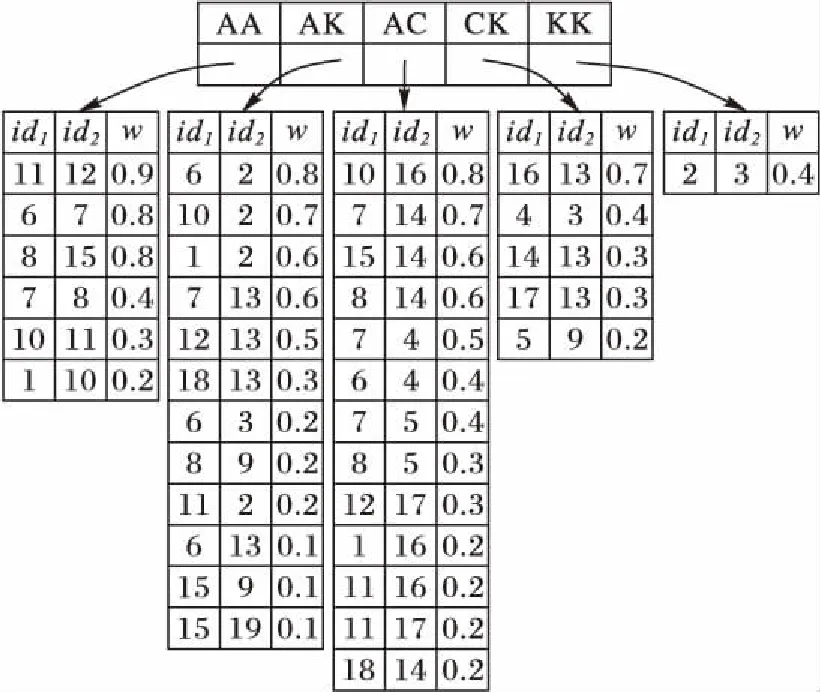
图4 EF索引Fig. 4 Index of EF
2.3 基于GTSF索引的多因素候选集过滤
子图匹配验证的效率与构建的索引和候选集的过滤策略密切相关,利用高效的图索引和过滤策略过滤掉明显违背查询需求的元素,获得相对较小的候选集,可提高子图匹配验证的效率。因此,本文利用NTF索引和EF索引,针对节点和边分别给出候选节点集过滤策略(CNFiltering)和候选边集过滤策略(CEFiltering),以实现对节点及边的剪枝过滤。
2.3.1多因素候选节点集过滤
在大规模动态图中,用户常根据查询需求,通过对某边权值限制实现个性化查询。因此查询图中节点可区分为特殊节点(带有权值边的端点称为特殊节点)和普通节点,在进行候选节点筛选时,本文从节点类型、度、邻接点个数、边权值限制等多因素考虑,提出了CNFiltering策略,如算法1所示。
算法1CNFiltering algorithm。
输入node topology feature indexTG, edge feature indexEG, node topology feature indexTQ, edge feature indexEQ;
输出the candidate node setCN。
1)
CN=NULL;
2)
for(traverseeinEQ) do
/*遍历EF索引,获取查询图Q候选节点集CN*/
3)
if(w(e)!=0)
/*对特殊节点过滤*/
4)
CN←SNF(EG,e,CN);
5)
CN←DF(TG,e,CN);
6)
CN←ANLF(TG,e,CN);
7)
else
/*对普通节点过滤*/
8)
CN←DF(TG,e,CN);
9)
CN←ANLF(TG,e,CN);
10)
end for
11)
OutputCN;
1)特殊节点过滤(Special Node Filtering, SNF)。对于特殊节点,其构成的边必须满足查询图中权值的限制,因此根据加权边类型,利用EF索引,将不满足权值限制的边进行剪枝,以筛选出特殊节点候选集。
2)度过滤(Degree Filtering, DF)。候选集中各节点度不小于查询节点度,因此利用NTF索引,根据查询节点类型及度剪枝无效节点。
3)邻接点标签频率过滤(Adjacent Node Label Frequency Filtering, ANLF)。候选节点不仅要满足度的要求,同时每种类型邻接点数都不小于对应查询节点中同类型邻接点数,为此,利用NTF索引在DF基础上剪枝不满足邻接点各类型出现频率的节点,从而获得候选节点集。
以图2中数据图及查询图为例,Q中仅AC类型的边(v1,v2)具有权值0.5,因此v1和v2为特殊节点,检索EF索引,获得边权值不小于0.5的AC类型的边为(10,16):0.8、(7,14):0.7、(15,14):0.6、(8,14):0.6和(7,4):0.5,再对其进行DF过滤和ANLF过滤,获得v1和v2的候选集分别为{10,15,7,8}和{16,14,4}。对于普通节点仅使用DF过滤和ANLF过滤获取节点的候选集,最终获得查询图Q的候选节点集CN如图5所示。
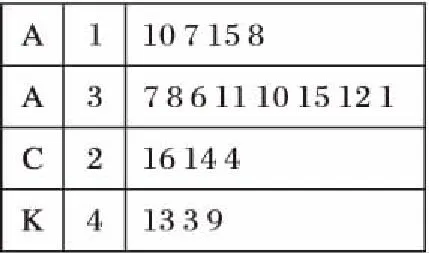
图5 查询图Q的候选节点集CNFig. 5 Candidate node set CN of query graph Q
2.3.2候选边集过滤
利用CNFiltering策略可有效剪枝去除不满足要求的节点,获得相对较少的查询图节点候选集。本节在候选节点集基础上,利用数据图的EF索引,充分挖掘节点和边所蕴含的信息,提出候选边集过滤策略,即CEFiltering,以实现对查询图候选集再一次剪枝,获得更优的用于最终子图匹配验证的候选边集。
1)特殊边过滤。在查询图中,带有权值的边为特殊边,针对每条特殊边检索数据图的EF索引,筛选边类型相同且权值不小于特殊边权值的边作为候选边;然后判断候选边的两端点是否在相应的候选节点集中,存在为有效边,反之则无效,进而获得特殊边的候选边集。
2)普通边过滤。在查询图中,无权值的边为普通边,对普通边的过滤仅需根据边的类型检索数据图的EF索引,找到类型相同的边并且边的两个端点应在对应的节点候选集中,从而获得普通边的候选集。
仍以图2为例,查询图Q有AA、AC和CK三种类型的边。其中只有AC类型的边(v1,v2)带有权值0.5, 利用EF索引找到AC类型的权值不小于0.5的边,且满足边端点在CN中,因此(v1,v2)边的候选集为{(10,16):0.8,(7,14):0.7, (15,14):0.6,(8,14):0.6,(7,4):0.5}。Q中CK类型的边(v2,v4)为普通边,检索EF索引,找到CK类型的边且两端点在对应v2和v4节点候选集中的边,获得(v2,v4)的候选边集为{(16,13),(4,3), (14,13)}。同理获得其他普通边候选集。查询图Q的候选边集CE如图6所示。
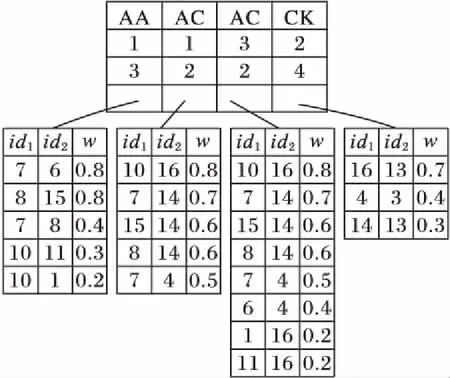
图6 查询图Q的候选边集CEFig. 6 Candidate edge set CE of query graph Q
2.4 兴趣子图匹配验证
在进行Top-K兴趣子图匹配验证时,图的动态变化可能对匹配结果产生影响,因此为尽量保证查询结果的准确性,本文将匹配过程分为初始匹配和动态修正两个阶段。
初始匹配验证将在候选边集CE之上进行。由于匹配验证采用逐一边匹配的方式,因此将最小候选边集对应边作为起始匹配边进行广度优先遍历,可有效减少迭代次数,进而减少不必要的计算开销。在介绍匹配验证之前,首先介绍Size-c候选匹配及其上界值计算US(Size-c)两个概念。
定义2Size-c候选匹配。一个Size-c候选匹配表示在子图匹配中,对查询图的c条边进行实例化的部分增长匹配,其兴趣度为实例化边的权值之和,其中c∈(1,n),n为查询图的边数。
定义3US(Size-c)。又称Size-c候选匹配的兴趣度上界值,其值为Size-c候选匹配中实例化边的权值与没有实例化边的最大候选边的权值之和。
初始匹配验证具体过程如算法2。算法维护一个Top-K堆用于降序存储兴趣度最大的K个匹配结果;维护候选匹配堆CM用于升序存储子图匹配验证过程中已经验证存入Top-K堆但被之后的匹配结果替换的匹配,以及已经验证但未存入Top-K堆的匹配。
算法2InitSubMatching algorithm。
输入edge feature indexEQ, the candidate edge setCE, number of interesting subgraphK;
输出Top-Kinteresting subgraphF, the candidate matching heapCM。
1)
CM=NULL;F=NULL;
2)
intCP,N=|EQ|,Top-K=K,O[|EQ|];
3)
O[0] ←First(CE);
/*确定起始边*/
4)
O[ ]←traverseEQfromCE;
/*确定边匹配顺序*/
5)
for((u,v)′←traverseCE[O[0]]) do
/*实例化查询图Q,获得初始Top-K堆*/
6)
CP←Size-1((u,v)′);
7)
if(US(Size-1) 8) return false; 9) else 10) for(c=2,3,…,n) do 11) (u,v)″←traverseO[c] in |CP|; 12) if((u,v)″ !=null) 13) (u,v)″←traverse|CP|; 14) CP←Size-c(); 15) else return false; 16) end for 17) if(I(Size-n())<=I(Top-K.bottom)) 18) CM←Size-n(); 19) update(CM); 20) return false; 21) else 22) CM←Top-K.bottom; 23) update(CM); 24) delete(Top-K.bottom); 25) Top-K←Size-n(); 26) update(Top-K); 27) end for 28) F←Top-K; 29) OutputF,CM; 针对图2中的数据图G和查询图Q,Top-K子图匹配的K为2时的初始匹配过程:首先遍历候选边集CE,确定起始边为(v2,v4),从边(v2,v4)开始进行广度优先遍历以获得查询图边的匹配顺序为(v2,v4)→(v1,v2)→(v3,v2)→(v1,v3);按照(v2,v4)边的匹配顺序实例化,先将(v2,v4)实例化为(16,13):0.7,则Size-1候选匹配为(v1,16,v3,13):0.8,接着进行Size-c(c=2,3,…,n,n为查询图Q的边数),获得(10,16,1,13):1.9、(10,16,11,13):2.0两个匹配子图,将其存入Top-K堆中,继续实例化获得其他匹配;当Top-K堆满时根据兴趣度更新Top-K堆,以获得初始匹配结果,同时将CM堆的子图作为备用候选子图。 节点或边的插入、删除、更改权值均导致图的动态变化,而图的变化可能影响查询结果,为此本文将利用更新间隔内的图变化对初始匹配结果进行动态修正,在保证查询效率的基础上进一步提高查询结果的准确性。将更新间隔内的图变化记录收集形成待更新记录集W。对于W内的插入记录,以插入记录对应边为起始边,按照广度优先遍历进行实例化,用得到的匹配子图更新Top-K堆和备用候选子图,获得最终匹配结果(Top-K堆内的子图);对于W内的删除记录,若在Top-K堆和备用候选子图中存在相关的节点或边,则将对应候选子图删除,并用修改后的备用候选子图中兴趣度最大的子图填满Top-K堆,获得查询结果;对于W内的更改权值记录,若Top-K堆或备用候选子图中存在相关的节点或边,则将重新比较变化子图与其他子图的兴趣度,用前K个更新Top-K堆,作为最终查询结果。 本章将本文的DISQtop-k方法与目前具有代表性的RAM、RWM算法进行实验对比,比较并分析不同数据量级的数据集上索引创建时间、索引存储开销及子图查询效率。 本文实验环境为Intel Pentium CPU G3220@3.00 GHz处理器、4 GB内存,500 GB硬盘,编程语言为Java,开发环境为eclipse 6.5。 实验分别在DBLP真实数据集及模拟数据集上完成。真实数据集利用NetClus[15]聚类方法将DBLP数据聚类成由作者、关键字和会议组成的作者合作关系网。将DBLP数据集(节点数为217 080,边数为1 022 980)分为3个子集合GR1(包括104个节点,13 774条边,约1万个节点规模)、GR2(包括105个节点,392 482条边,约10万个节点规模),GR3(包括217 080个节点,1 022 980条边,约22万个节点规模)。模拟数据集G1、G2、G3和G4则通过GT-Graph的图生成器R-MAT[16]创建,其节点数分别为103、104、105和106,每个图的边数为其节点的10倍,每个节点从1到5随机分配属性标签性,每条边的权值随机产生[0,1]区间的值。 3.2.1索引创建时间及存储开销 图7(a)和(b)分别展示了模拟数据集上和真实数据集上不同索引的构建时间对比情况。RAM算法需建立SPath索引,RWM算法需建立Topology、MMW索引。如图7所示,各索引创建时间均随图规模的增大而增长。其中EF索引创建时间远小于其他索引,这是因为其只需对不同的标签边进行排序,无需计算复杂的节点关系等;NTF索引明显优于Topology+MMW(D=2)和SPath索引,因为NTF索引仅需遍历一次数据图即可获得所有节点及其邻接点的关系,然而Topology+MMW(D=2)和SPath索引受D的约束,随着D值的增加,索引构建时间将会呈指数增长。 图7 不同数据集上的索引构建时间对比Fig. 7 Index building time comparison for different datasets 表1展示了在模拟数据集和真实数据集上不同索引的存储开销。各索引的存储空间均随图规模的增大而变大,其中NTF及EF索引所占的内存较少,因为NTF索引仅需要存储各节点的度及一跳邻接点信息,而EF索引只记录边的权值信息;而SPath、MMW和Topology 则根据D值的不同,需要记录各节点多跳邻接点信息,因此随着D值的增加,索引的存储空间将呈指数增长。 表1 不同数据集上的索引存储空间对比 KBTab. 1 Index size comparison for different datasets KB 表2 不同数据集上的算法查询时间的比较 sTab. 2 Query time comparison for different datasets s 3.2.2兴趣子图查询效率分析 表2展示了在不同规模数据集下查询时间对比情况。实验针对无权查询图(Q1)和加权查询图(Q2),观察随数据图规模的增大,各种算法的查询时间变化情况。其中,Q1是图2(b)中查询图Q去除权值后的图,Q2是图2(b)中查询图Q,RAM和RWM索引中D=2。 从表2可以看出,各种算法的查询时间随着数据规模增大而增大。 RAM和RWM算法对于有权查询图的查询,需要首先查询所有匹配子图后再进行满足权值限制子图的筛选,而DISQtop-k算法则在候选集筛选时已过滤不满足条件的节点及边,避免了重复计算,所以运行时间更短、增长较平缓。 3.2.3查询图变化对子图查询效率的影响 分析可知,查询图节点个数以及K值的设定均对子图查询时间具有一定的影响,表3展示了在模拟数据集G2和DBLP数据集的子集GR1上,DISQtop-K针对不同规模的查询图Q及不同K值设定下查询时间对比情况。 从表3中可以看出,当查询图及K值的增大,查询时间均随之增加。当查询图Q相同时,不同的K值间的查询时间波动较小。 表3 不同数据集上的DISQtop-k算法针对不同查询图、K值的查询时间对比Tab. 3 Query time comparison of different query graph and K value by DISQtop-K algorithm for different datasets 本文提出一种适用于大规模动态标签图中的Top-K兴趣子图查询方法,即 DISQtop-K方法。该方法首先建立由NTF和EF索引构成的GTSF索引,基于该索引提出了多因素候选集过滤策略,对查询图候选集进行有效剪枝;充分考虑图动态变化下产生的查询误差,对候选集进行初始匹配及动态修正以获得查询结果。真实数据集及模拟数据集上的实验结果表明,该方法在大规模动态标签图上具有较高的查询效率,且查询结果具有一定的实际意义。 参考文献: [1]SONMEZ A B, CAN T. Comparison of tissue/disease specific integrated networks using directed graphlet signatures [J]. BMC Bioinformatics, 2017, 18(Suppl. 4): 135. [2]张海威,解晓芳,段媛媛,等.一种基于自适应结构概要的有向标签子图匹配查询算法[J].计算机学报,2017,40(1):52-71. (ZHANG H W, XIE J F, DUAN Y Y, et al.An algorithm for subgraph matching based on adaptive structural summary of labeled directed graph data[J]. Chinese Journal of Computers, 2017, 40(1): 52-71.) [3]ULLMANN J R. An algorithm for subgraph isomorphism [J]. Journal of the ACM (JACM), 1976, 23(1): 31-42. [4]CORDELLA L P, FOGGIA P, SANSONE C, et al. A (sub)graph isomorphism algorithm for matching large graphs [J]. IEEE Transactions on Pattern Analysis & Machine Intelligence, 2004, 26(10): 1367-1372. [5]SUN Z, WANG H, WANG H, et al. Efficient subgraph matching on billion node graphs [J]. Proceedings of the VLDB Endowment, 2012, 5(9): 788-799. [6]HAN W-S, LEE J, LEE J-H. TurboISO: towards ultrafast and robust subgraph isomorphism search in large graph databases [C]// SIGMOD ’13: Proceedings of the 2013 ACM SIGMOD International Conference on Management of Data. New York: ACM, 2013: 337-348. [7]REN X, WANG J. Exploiting vertex relationships in speeding up subgraph isomorphism over large graphs [J]. Proceeding of the VLDB Endowment, 2015, 8(5): 617-628. [8]BI F, CHANG L, LIN X, et al. Efficient subgraph matching by postponing Cartesian products [C]// SIGMOD ’16: Proceedings of the 2016 International Conference on Management of Data. New York: ACM, 2016: 1199-1214. [9]HOLDER L B, COOK D, DJOKO S. Substructure discovery in the SUBDUE system [C]// AAAIWS’94: Proceedings of the 3rd International Conference on Knowledge Discovery and Data Mining. Seattle, WA: IAAA, 1994: 169-180. [10]ZHU F, QU Q, LO D, et al. Mining Top-Klarge structural patterns in a massive network [J]. Proceedings of the VLDB Endowment, 2011, 4(11): 807-818. [11]ZHAO P, HAN J. On graph query optimization in large networks [J]. Proceedings of the VLDB Endowment, 2010, 3(1/2): 340-351. [12]HE H, SINGH A K. Query language and access methods for graph databases [M]// Managing and Mining Graph Data. Boston: Springer, 2010: 125-160. [13]YAN X, HE B, ZHU F, et al. Top-Kaggregation queries over large networks [C]// ICDE 2010: Proceedings of the 2010 IEEE 26th International Conference on Data Engineering. Washington, DC: IEEE Computer Society, 2010: 377-380. [14]GUPTA M, GAO J, YAN X, et al. Top-Kinteresting subgraph discovery in information networks [C]// ICDE 2014: Proceedings of the 2014 IEEE 30th International Conference on Data Engineering. Washington, DC: IEEE Computer Society, 2014: 820-831. [15]SUN Y, YU Y, HAN J. Ranking-based clustering of heterogeneous information networks with star network schema [C]// KDD ’09: Proceedings of the 15th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining. New York: ACM, 2009: 797-806. [16]CHAKRABARTI D, ZHAN Y, FALOUTSOS C. R-MAT: a recursive model for graph mining [C]// SIAM International Conference on Data Mining. Philadelphia, PA: Society for Industrial and Applied Mathematics (SIAM), 2004: 442-446.3 实验与分析
3.1 实验环境及数据集
3.2 实验分析
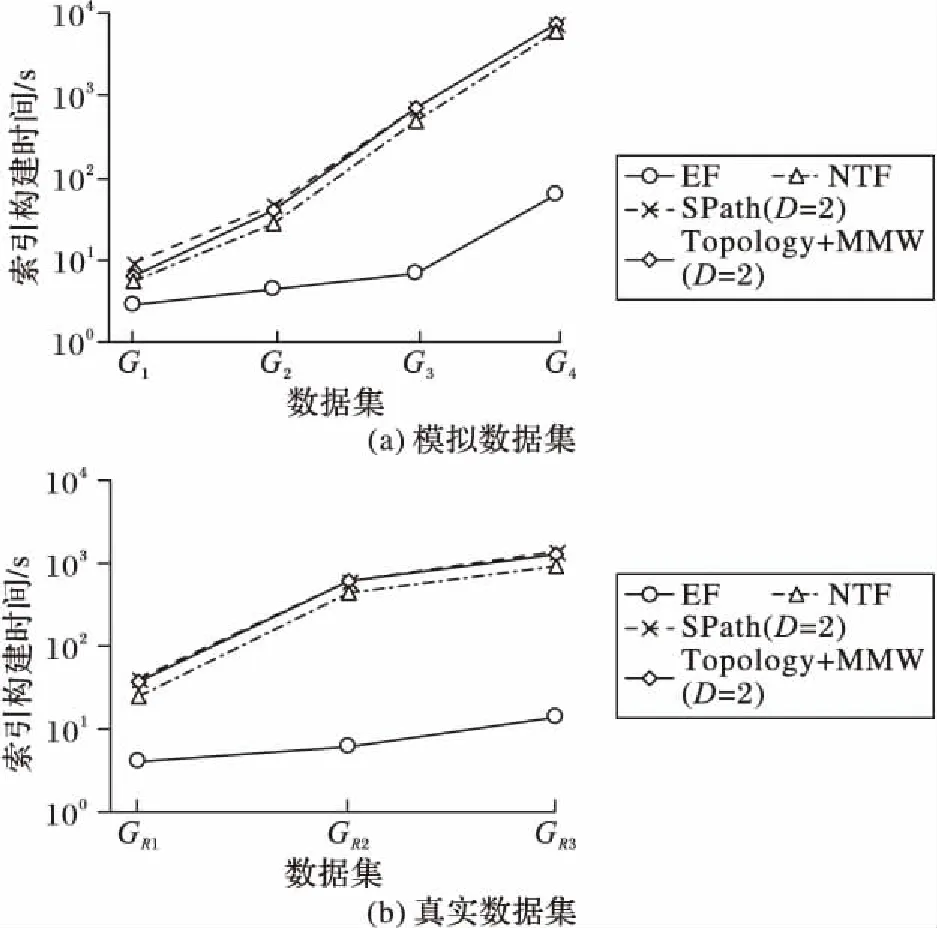


4 结语

