基于耦合多隐马尔可夫模型和深度图像数据的人体动作识别

张全贵，蔡　丰，李志强

(辽宁工程技术大学 电子与信息工程学院，辽宁 葫芦岛 125105)(*通信作者电子邮箱545130868@qq.com)

0　引言

人体动作识别是为了让计算机通过一些方法判别出捕捉到的人体动作类别，在行为科学[1]、社交媒体等方面得到了广泛的应用及发展，如智能视频监控、家庭服务机器人[2]等。在微软公司发布Kinect之后，使得获取的图像数据受较少外部因素干扰而更为准确，因此近年来基于深度图像数据的人体动作识别成为一个研究热点。例如，申小霞等[3]利用Kinect获取图像信息及金字塔特征来描述行为信息，并且通过使用支持向量机(Support Vector Machine,SVM)算法进行行为分类；Shotton等[4]提出一种新的方法从一个单一的深度图像预测人类姿势，该方法基于当前目标识别策略，通过设计中间表示部分把复杂姿态问题化为简单问题；张毅等[5]将行为识别应用到医疗康复训练方面，同样采用Kinect采集数据，同时使用了朴素贝叶斯模型，并通过调整模型阈值提高识别率。

以上这些方法都具有一定的优势，并且能达到较好的识别效果。但现有的基于人体关节点进行人体动作识别的研究一般假设关节点之间是相互独立的，即没有考虑关节之间的相互关系。根据人体运动解剖学，人体在完成某个动作的时候各个关节点之间是相互制约和协同工作的，即关节点之间具有一定的耦合关系[6]。例如，从桌子上拿起水杯这个动作，胳膊的肘部活动一定会影响到手腕的活动。如果忽略各部位之间的交互，这样分析可能会导致大量信息的损失，因此本文将考虑人体各部分之间的相互影响关系，即耦合关系。建立人体动作的多隐马尔可夫模型(multi-Hidden Markov Model, Multi-HMM)，并运用耦合相似度分析与K最邻近(K-Nearest Neighbors, KNN)算法[7]进行基于耦合的人体动作识别，以便充分利用人体各个关节点之间的协同交互关系。

1　特征值提取

本文将Kinect提取的人体20个节点分成5个区域，从上到下、从左到右依次为左上肢、躯干、右上肢、左下肢和右下肢，分别用R1、R2、R3、R4和R5来表示。在每个区域中选取合适的向量及夹角，通过对向量夹角的划分进行特征值的提取，完成人体动作特征的描述。

人体各关节点名称如图1(a)所示；为方便描述将每个节点名称用英文字母代替全称，如图1(b)所示。例如，在R1区域内，节点c与节点d形成向量Vcd，节点c与节点b形成向量Vcb，向量Vcd与向量Vcb所形成夹角用Acd-cb表示。在其他四个区域以同样的方式选取向量及夹角。具体所选的向量如表1所示。

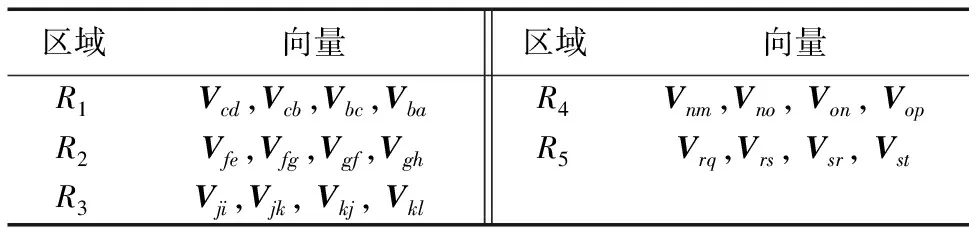
表1　选取向量Tab. 1　Selected vectors

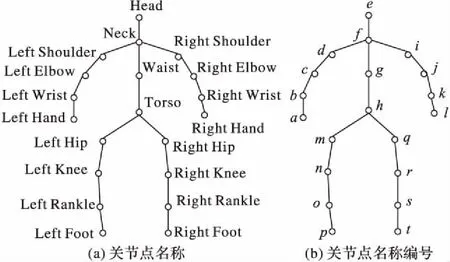
图1　关节点名称和编号示意图Fig. 1　Schematic diagram for name and label of joint nodes

在空间坐标系中左上肢与右上肢相对应，左下肢与右下肢对应，结合实际情况活动的范围大致相同，所以会有相同的角度划分。例如在区域R1中，左上臂与左前臂活动角度的范围比较大，所以设置的角度范围是最小0°到最大180°，以间隔为20°将此区间划分成9个区间，依次编号为0～8。左前臂与左手动作范围较小，所以设置为0°到90°，间隔区间为10°，同样将此范围划分成9个区间，编号为0～8。右上肢将有与左上肢相同的角度划分。本文将五个区域中的向量夹角均划分成9个区间，编号为0～8 。经过实验分析得到每个角度的最佳变化范围及划分区间如表2所示。

表2　角度划分Tab. 2　Angle division

当求两个空间向量之间的夹角时，需要使用余弦函数，例如有向量a=(x1,y1,z1)和向量b=(x2,y2,z2)，则向量a、b之间夹角可以由式(1)计算得到:

(1)

其中|a|≠0，|b|≠0。如果|a|≠0且|b|≠0，而a·b=x1x2+y1y2+z1z2，|a|2=x12+y12+z12，则〈a,b〉=0，即a和b为正交向量。例如，通过式(1)求得某个区域的一个夹角大小为23°时，根据角度及编号的划分可以得到：当此向量角处于0°～180°范围时，它对应的编号为1 ；当此向量角处于0°～90°范围时到此角度对应标号为2 。

本文将取T帧视频序列，每个分区将形成一个观察序列(or1,or2,…,orT)，其中r表示分区，取值为{1,2,…,5} 。

2　动作识别

2.1　基于隐马尔可夫模型的局部分类

最初的隐马尔可夫模型(Hidden Markov Model, HMM)[8]是在统计学中提出的。一个HMM包含两组状态集合和三组概率集合,可以用五个元素来描述，记为λ=(S,O,π,A,B)。其中：S表示隐含状态，所有隐含状态之间满足马尔可夫性；O表示可观测状态；π表示初始状态概率矩阵；A表示隐含状态转移概率矩阵；B表示观测状态移概率矩阵。也可以将HMM用一个三元组(π,A,B)来表示。

在第1章中已经获取了每个分区的观测序列，接下来将使用Baum-Welch算法训练得到各个分区的多个HMM，并使用前向算法计算观察序列的概率。具体流程如下：

算法1分区训练HMM并计算观察序列概率。

输入分区观察序列O={ort}，其中r={1,2,…,5}，1≤t≤T。

过程：

1)初始化参数模型λ0。

2)根据式(2)计算t+1时刻状态为j的概率。

εt(i,j)=P(qt=i,qt+1=j/O,λ)=

(2)

其中:1≤i≤N，1≤j≤N，1≤k≤M，N表示隐含状态的个数，M表示观测状态的个数;βt+1(j)表示后向概率。

3)根据式(3)计算t时刻状态i的概率。

(3)

其中:1≤i≤N，1≤t≤T。

4)根据式(4)、(5)、(6)计算分别得到模型的三个参数值，即能获得模型λi+1。

πt(i)=γt(i)

(4)

(5)

其中:1≤i≤N，1≤j≤N，1≤t≤T-1。

(6)

其中:1≤j≤N，1≤k≤M。

5)重复步骤2)、3)、4)，循环迭代直到πt、aij、bjk三个参数收敛，为这次训练的最终模型。

6)模型训练结束后，取新的观察序列。使用前向算法：当t=1时，根据式(7)计算局部概率;当t>1时，采用递归的方法，根据式(8)计算当前HMM下一个观察序列的概率。

a1(j)=π(j)bjk1

(7)

(8)

7)根据式(9)计算给定观察序列的概率等于T时刻所有局部概率之和。

(9)

输出结果为当前的观察序列在HMM下的概率值。

2.2　基于HMM的局部分类

观察序列输入到模型后会计算得到概率矩阵如下：P={pxy}，pxy表示第x分区中第y个HMM对观察序列的概率，其中x、y取值均为{1,2，…,5}。

当某个动作发生时，通过矩阵P可以知道是身体哪个区域发出这个动作，但是并不能知道此动作是由身体的单一区域还是多个区域共同完成。基于以上工作，通过进一步分析各个概率值之间耦合关系，并使用基于耦合的KNN算法得到最终的动作分类。因此需要分析处理：将得到的矩阵P变换成25维的向量，即(p11,p12,…,p15,p21,p22,…,p25,…,p51,p52,…,p55)，并且这个向量在训练数据中有相应的分类标签。每一个视频序列都形成一个向量，那么取m个视频序列{s1,s2,…,

sm}便可以得到m个25维向量。本文共取100个视频序列。每一维看作一个属性，计算各属性的内耦合及间耦合关系，通过属性的内耦合及间耦合来分析各个动作序列之间的隐含关系。本文借鉴文献[6]的方法计算内耦合、间耦合。

2.2.1内耦合分析

本节将属性值af扩展出L-1个属性值，本文的L取值为2，分别为〈af〉2，〈af〉3，…, 〈af〉L，那么属性值af的内耦合关系可以表示成L×L的矩阵R-Ia(af)，其中〈af〉v表示属性af的v次幂。

(10)

其中：φpq(f)=Cor(〈af〉p,〈af〉q)是属性〈af〉p和属性〈af〉q的皮尔逊相关系数。属性af和ag之间的皮尔逊相关系数为：

Cor(af,ag)=

其中μf、μg分别表示属性值af、ag的均值。

2.2.2间耦合分析

假设有n个属性值(这里n=25)，将每一个属性值af都扩展出L-1个属性值：〈af〉2，〈af〉3，…, 〈af〉L，〈af〉v表示属性af的v次幂。那么数值型属性af与属性ag及属性〈af〉v(f≠g)的间耦合关系可以表示为大小为L×(L×(n-1))的矩阵R-Ie(af|{ag}g≠f)。计算公式如下：

2.2.3对象的耦合表示及KNN分类

对象u在其他的属性值上的向量为：

由公式可以得到对象u在属性af上的1×L向量：

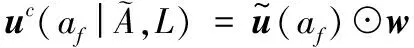
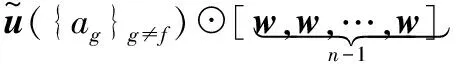
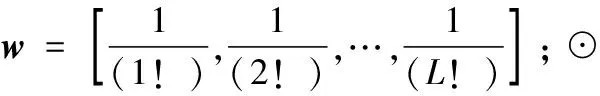
到此，已完成了多个HMM形成的概率矩阵的耦合相似性分析。基于此，使用KNN算法完成最后的人体动作分类。在使用KNN算法时，使用以上介绍的对象耦合相似度计算方法代替传统的欧氏距离方法。

3　实验分析

3.1　实验数据集及实验过程

实验在公开数据集MSR-Daily-Activity 3D(MSR Daily Activity 3D Dataset)[9]上进行。MSR-Daily-Activity 3D数据集中包含16种人体动作，每种动作分别由10个人来做，每类动作做2次，一共有320个样本。该数据集是在客厅中录制的，基本上涵盖了人类的日常活动。行为者是站在沙发附近完成的各种动作，使得骨骼追踪非常复杂，因此使得这个数据集更具有挑战性。该数据集同时提供了三种数据信息：深度图像、骨骼关节位置和RGB视频，本文选择骨骼关节位置中的drinking、cheer up、walk、sit down和stand up共5种动作的数据进行实验。

实验时取出上述5种动作序列的数据集后分成训练数据集与测试数据集两组，其中第一个到第八个人的动作数据集用作训练，第九、第十这两个人的动作数据集用作测试。为避免过拟合现象，本文从这些数据集中按照等间距标准从原视频序列选取关键帧组成新的序列。根据第2章中特征提取方法把每种视频序列用矩阵表示，进行HMM训练得到参数λi，再利用前向算法计算观察序列的概率即完成分区动作识别，最后根据基于耦合关系的KNN算法完成整体的动作识别。

3.2　实验结果与分析

本文动作识别算法的动作识别率结果如表1所示，均在90%以上，其中walk的识别率最高为96.86%，这说明本文算法的识别率水平较高。

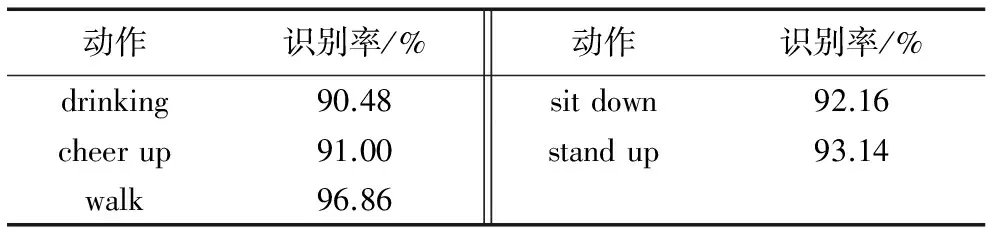
表3　动作识别率Tab. 3　Recognition rates of actions

为了进一步验证本文算法的有效性，将其与同样使用此数据集进行实验的文献[10-12]的方法对所有动作的综合识别率进行比较。其中，文献[10]的实验中将动作分为了两类，一类是低运动动作，另一类是高运动动作，两种类型的识别率分别为60%和85%。由于本文所选取的动作属于高运动动作，所以只考虑与文献[10]中高运动动作的识别率比较。文献[11]的数据获取较为复杂，且整体计算量较大，其设置了多组实验，因此这里取平均值与本文方法进行比较。文献[12]使用的是骨骼形状轨迹的方法，而MSR-Daily-Activity 3D数据集本身所处的环境较复杂，所以在使用骨骼追踪时比较困难，以至于识别率较低。本文取与文献[12]相同的实验设置，即取前5个人作为训练，后5个人作为测试。

经过实验，本文方法的综合识别率为87.16%，3D Trajectories方法[10]识别率为85%，Actionlet Ensemble Model方法[11]识别率为85.75%，Skeletal Shape Trajectories方法[12]识别率为70.00%。可以看出，本文所提出的识别方法与其他三种方法相比具有较高的识别率，并且达到了较好的预期识别效果，由于能够在复杂的环境下表现良好，所以体现出了较强的鲁棒性。

4　结语

本文使用关节点角度值描述特征，通过Baum-Welch算法建立多HMM得到相应参数，根据前向算法对人体分区进行动作识别，然后利用基于耦合关系的KNN算法完成整体的动作识别，充分利用了人体的各个部分之间的隐含交互关系。实验结果表明本文提出的方法具有一定的优越性。

本文方法只识别了五种动作，没有对更复杂背景下的复杂动作进行识别验证，这将是我们要继续研究的内容。

参考文献:

[1]ZACHARIAS G L, MacMILLAN J, VAN HEMEL S B, et al. Behavioral modeling and simulation: from individuals to societies [J]. Journal of Artificial Societies & Social Simulation, 2008, 12(3): 291-304.

[2]田国会,尹建芹,韩旭,等.一种基于关节点信息的人体行为识别新方法[J].机器人,2014,36(3):285-292. (TIAN G H, YIN J Q, HAN X, et al. A new method of human behavior recognition based on joint information [J]. Robot, 2014, 36(3): 285-292.)

[3]申小霞,张桦,高赞.基于Kinect和金字塔特征的行为识别算法[J].光电子·激光,2014(2):357-363. (SHEN X X, ZHANG H, GAO Z. Behavior recognition algorithm based on Kinect and pyramid feature[J]. Journal of Optoelectronics · Laser, 2014(2): 357-363.)

[4]SHOTTON J, FITZGIBBON A, COOK M, et al. Real-time human pose recognition in parts from single depth images [C]// CVPR 2011: Proceedings of the 2011 IEEE Conference on Computer Vision and Pattern Recognition, SCI 411. Washington, DC: IEEE Computer Society, 2011: 1297-1304.

[5]张毅,黄聪,罗元.基于改进朴素贝叶斯分类器的康复训练行为识别方法[J].计算机应用,2013,33(11):3187-3189. (ZHANG Y, HUANG C, LUO Y. Rehabilitation training behavior recognition method based on improved naive Bayesian classifier [J]. Journal of Computer Applications, 2013, 33(11): 3187-3189.)

[6]WANG C, SHE Z, CAO L. Coupled attribute analysis on numerical data [C]// IJCAI ’13: Proceedings of the 2013 International Joint Conference on Artificial Intelligence. Menlo Park, CA: AAAI Press, 2013: 1736-1742.

[7]FIGUEIREDO F, ROCHA L, COUTO T, et al. Word co-occurrence features for text classification [J]. Information Systems, 2011, 36(5): 843-858.

[8]MOGHADDAM Z, PICCARDI M. Training initialization of hidden markov models in human action recognition [J]. IEEE Transactions on Automation Science & Engineering, 2014, 11(2): 394-408.

[9]WANG J, LIU Z, WU Y, et al. Mining actionlet ensemble for action recognition with depth cameras [C]// CVPR 2012: Proceedings of the 2012 IEEE Conference on Computer Vision and Pattern Recognition. Washington, DC: IEEE Computer Society, 2012: 1290-1297.

[10]KOPERSKI M, BILINSKI P, BREMOND F. 3D trajectories for action recognition [C]// ICIP 2014: Proceedings of the 2014 IEEE International Conference on Image Processing. Piscataway, NJ: IEEE, 2014: 4176-4180.

[11]LI W, ZHANG Z, LIU Z. Action recognition based on a bag of 3D points [C]// CVPRW 2010: Proceedings of the 2010 IEEE Computer Society Conference on Computer Vision and Pattern Recognition Workshops. Washington, DC: IEEE Computer Society, 2010: 9-14.

[12]AMOR B B, SU J, SRIVASTAVA A. Action recognition using rate-invariant analysis, of skeletal shape trajectories [J]. IEEE Transactions on Pattern Analysis & Machine Intelligence, 2016, 38(1): 1-13.