两个电子货币方案的分析与改进

邵栋阳，亢保元，王佳强

(天津工业大学 计算机科学与软件学院，天津 300387)(*通信作者电子邮箱dongyang_shao@163.com)

0　引言

得益于互联网技术的飞速发展，电子货币方案作为一种重要的支付手段，逐步得到了人们的重视。Chaum借助盲签名的思想构造了第一个电子货币方案[1]并对电子货币方案进行了深入研究[2-3]。大部分电子货币使用盲签名构造，传统公钥签名使用证书，为了减少证书和证书管理的成本，Shamir[4]提出了基于身份的密码体制，Al-Riyami等[5]提出了无证书公钥密码，Abe等[6]提出了部分盲签名概念。目前电子货币方案的主要研究集中在如何保证安全性和提高效率上。一个安全的电子货币方案应该满足公平性、不可伪造性、不可追踪性、匿名性和不可重复花费等特性[7]。

一个传统的电子支付协议需要三个参与者：顾客、银行和商家。当顾客想从商家那里买东西时，首先计算商品所需价格并向银行申请取款；然后由银行核实顾客身份后制作签名货币并发给顾客；最后，顾客用得到的电子货币与商家进行交易。顾客和商家交易过程中需要银行参与的方案称为在线电子货币方案，而交易过程中不需要银行参与的方案称为离线电子货币方案。在线电子货币能够更好地避免电子货币的二次花费，但是交易阶段银行的介入会大大降低方案的效率。所以，目前主流方案基本都是离线电子货币方案[8-10]，但离线电子货币方案需要一种有效的二次花费检测和追踪方法。

随着互联网的发展，人们热衷于网上购买音像等数字商品。在针对数字商品的电子货币方案中，为了保证公平性，一般还需要一个仲裁者。当出现顾客或商家违反方案条款的行为，产生交易纠纷时，仲裁者可以出面支持公道，并解决纠纷。例如，当出现顾客把电子货币发给商家，而商家没有给顾客数字商品这种情况时，顾客可以请求仲裁者仲裁，以讨回购买的数字商品。因此，公平性是面向数字商品的电子货币方案的一个必不可少的安全特性。

2013年，Yang等[11]提出了一个认证加密方法，并使用这个认证加密的方法提出了一个电子货币方案，他们声称此方案能够抵抗重放攻击、中间人攻击、假冒攻击、身份盗窃攻击。然而，2015年Chaudhry等[12]指出Yang等的电子货币方案容易受到假冒攻击，并提出了一个改进方案。在研究了Chaudhry等的方案之后发现，该方案无法保证消费者的匿名性，同时也无法解决交易纠纷和实现二次花费追踪。2015年,Liu等[13]提出了一个基于银行代理的离线电子货币方案，笔者在研究后发现该方案中的用户可以伪造电子货币。本文在指出基于椭圆曲线认证加密方案和银行委托离线电子货币方案中缺点的同时，对这两个电子货币方案提出了相应的改进方案。

1　预备知识

1.1　椭圆曲线

设Fp是p阶有限域，其中素数p≥2160，a,b∈Fp，并满足Δ=4a3+27b2≠0。椭圆曲线是指满足方程y2=x3+ax+b的点和一个无穷远点的集合。本文中使用椭圆曲线上的点(kx,ky)的横坐标kx作为密钥进行加密。

1.2　双线性对

设q为一个大素数，G1为q阶的加法循环群，G2位q阶的乘法循环群，p为G1的生成元，e:G1×G1→G2是一个双线性映射，它具有以下性质：

1)双线性性：对于任意P,Q,R∈G1和a,b∈Zq都有：

e(P+Q,R)=e(P,R)e(Q,R)

e(aP,bQ)=e(P,abQ)=e(abP,Q)=e(P,Q)ab

2)非退化性：存在P,Q∈G1使得e(P,Q)≠1。

3)可计算性：对于所有P,Q∈G1，存在计算e(P,Q)的有效算法。

1.3　困难性假设

1)离散对数问题：P,Q∈G1，Q=nP，已知P，Q求n在计算上是不可行的。

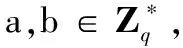
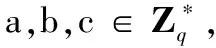
2　Chaudhry方案的不足与改进

2.1　Chaudhry方案

2.1.1初始化阶段

在这个阶段系统设置椭圆曲线Ep(a,b)，加密解密算法Ek(·)/Dk(·)，椭圆曲线的基点P，单向的哈希函数H，公开Ep(a,b),Ek(·),Dk(·),P,H，每个参与者i(i∈{b,m,u})都有自己的个人身份IDi和私钥di，并计算和公布公钥Yi=di×P。

2.1.2选购阶段

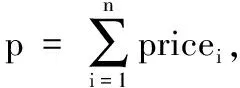
2.1.3取款阶段

当银行B收到(C1,R,T1)，首先计算K=dbR(Yu+T1P)=(kx,ky)，得到kx并解密Dkx(C1)=(IDu‖m‖p‖kx‖T1)。随后B检验时戳T1和kx是否和解密C1所得一致，如果一致则B验证有效，否则扔弃信息。随后B选一个有效期E并计算M=m‖E，并用私钥对M作签名DS，加密得C2=Ekx(DS‖E‖kx‖T2)。最后B把C2发送给U，并把{DS，M}存入数据库。

2.1.4交易阶段

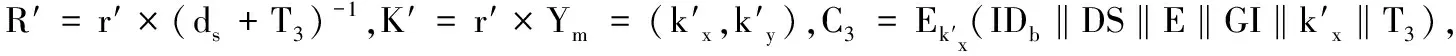
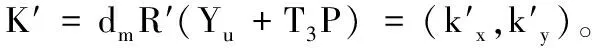
2.1.5存钱阶段

在有效期E之前，M需要把支付凭证发给银行B，U如果没有收到商品则有权向B申诉，B就会把钱从临时账户返还U账户。过了有效日期E之后，B会把钱转给M账户。然后，B把{DS,M}从其数据库中删除。

2.1.6纠纷解决阶段

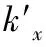
2.2　Chaudhry方案的不足

Chaudhry的方案宣称可以抵御重放攻击、仿冒攻击和中间人攻击，但笔者研究发现其方案主要有以下三个缺点：

1)系统不能保证匿名。

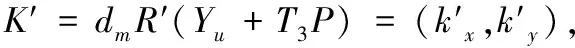
2)TTP无法解决纠纷。

在纠纷解决阶段,TTP需要得到商家M的私钥，但暴露自己的私钥是一件不安全的行为；并且顾客和商家进行申诉时，只能验证顾客和商家身份，并不能进行仲裁。

3)无法追踪二次花费。

在存钱阶段，在有效期E之前，商家M需要把支付凭证发给银行B，过了有效日期E之后，B会把钱转给M账户，然后把{DS,M}从数据库删除。如果在有效期之前顾客使用电子货币进行二次花费，则银行无法转账给商家也无法追踪二次花费。

2.3　Chaudhry方案的改进方案

针对Chaudhry方案的问题，提出以下改进方案，该方案主要由四个实体参与：银行B、顾客U、商家M和仲裁J，并由以下六个阶段组成：初始化阶段、取钱阶段、支付阶段、存钱阶段、二次花费追踪和纠纷仲裁。

2.3.1初始化阶段

在这个阶段系统设置椭圆曲线Ep(a,b)，加密解密算法Ek(·)/Dk(·)，椭圆曲线的基点P，单向的哈希函数H，公开Ep(a,b),Ek(·),Dk(·),P,H，每个参与者i都有自己的个人身份IDi和私钥di，并计算和公布公钥Yi=di×P。

2.3.2取钱阶段

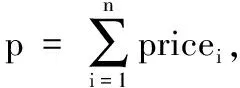
当银行B收到(C1,R,T1)，首先B计算K=dbR(Yu+T1P)=(kx,ky)，随后解密Dkx(C1)=(IDu‖m‖p‖kx‖r1‖r2‖T1)。然后B检验时戳T1和kx是否和解密C1所得一致。如果一致则B验证有效，否则扔弃信息。然后B从U账户取p转移至一个临时账户，随机选择α∈Zq，计算：V1=α·r1，V2=r2·Yb，V3=r1·Yb，V=α·IDu，选一个有效期E计算M=m‖V1‖V2‖V3‖E。然后B用私钥对M作签名DS，并计算C2=Ekx(DS‖E‖kx‖V1‖V2‖V3‖T2),最后B发送给U，并在数据库中存储{DS,M,V}。

2.3.3支付阶段

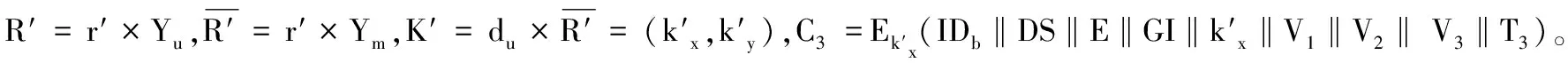
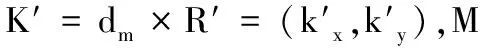
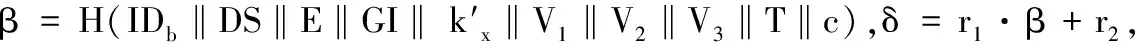
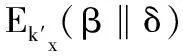
2.3.4存钱阶段

在有效期E之前，商家M需要把支付凭证{DS,β,δ,c}发给银行B，首先银行B检验DS是否使用过：如果没使用过则把p转到临时账户，并记录为使用过；如果使用过则进行二次花费追踪。U如果没有收到商品则有权向J申请仲裁。过了有效日期E之后，银行B把钱从临时账户转到商家M账户。

2.3.5二次花费追踪

假设两次花费凭证为{DS,β,δ,c}和{DS,β′,δ′,c}，银行查询数据库找到相应{DS,M,V}，从M中得到V1，并计算α=V1(β-β′)(δ-δ′)-1，IDu=α-1V即找到二次花费顾客。

首先，人际情绪管理受到社会标准和期待等文化因素的影响，不同文化背景下的个体在人际情绪管理方面存在显著的差异.相比个体主义文化，集体主义文化中的人们更多地关注他人的情绪，但是自己遇到情绪问题时，寻求外部支持的意愿却很小[23].因此，未来需要进一步开展跨文化研究，以增进对人际情绪管理的理解.

2.3.6纠纷仲裁

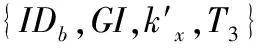
2.4　新方案的安全性分析

2.4.1正确性

取钱阶段，顾客U计算R=r(du+T1)-1和K=r×Yb=(kx,ky)，银行B计算：

K=dbR(Yu+T1P)=dbr(du+T1)-1(du+T1)P=

dbrP=r×Yb

支付阶段，顾客U计算：

δ=r1·β+r2

银行B算：

β·V3‖V3‖T‖c)=

r2·Yb-β·V3‖V3‖T‖c)=

由上可知验证等式正确。

2.4.2匿名性

在支付阶段用户U不需要把公钥Yu发给商家M，而是选择一个随机数r′来盲化自己的身份，从而在买商品时不会暴露自己的身份。银行存储的信息{DS,M,V}同样也不包含顾客身份，如没有二次花费，银行无法直接追踪到货币使用者。

2.4.3 重放攻击

假设攻击者截获顾客U发给银行B的(C,R,T)，想要把截获的信息再次发给银行B，银行B接收到(C,R,T)之后首先检验时戳T，如果过期，银行B直接丢弃信息。

2.4.4 假冒攻击

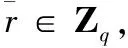
3　Liu方案的不足与改进

由于篇幅所限，本文不再详细回顾Liu等的方案，具体可参考文献[13]中的介绍。在该离线电子货币方案中有五个实体：中心银行O、分支银行P、仲裁J、顾客U和商家M。

3.1　Liu方案的不足

1)电子货币方案中取钱阶段，用户可以伪造电子货coin=(val,ω,R3,R4,R5,V)。

事实上，在取钱阶段第二步，用户可以取μ=aP-hPKP，μ1=bP-hH1(ω,RO)，V=aRO+b(PKO+PKP)，也可满足双线性映射验证等式：

e(V,P)=e(μ+hPKP,RO)·

e(μ1+hH1(ω,RO),PKO+PKP)

2)电子货币方案中取钱阶段，代理银行委托可信平台模块(Trusted Platform Module, TPM)计算验证，之后TPM把取钱金额传给代理银行P，如果用户账户余额不足，TPM则进行了无意义的计算，银行在委托TPM前没有验证余额是否充足。

3)电子货币方案中离线支付阶段，商家M不知道μ、μ1和RO，无法验证双线性等式。

3.2　Liu方案的改进

改进方案包括取钱阶段和离线支付阶段，其中初始化阶段、银行代理阶段、开户阶段、二次花费检测与原方案相同。

3.2.1取钱阶段

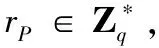
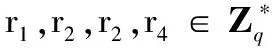
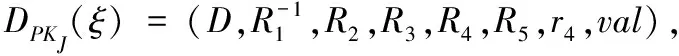
4)分支银行P验证TPM传来的val和之前顾客U传来的val是否相等，如果相等则P计算V′=(rP+D)dP，并把V′传给顾客U。

5)顾客U计算V=r1·V′，并验证e(V,P)?=e(μ+hPKP,RO)e(μ1+hH1(ω,RO),PKO+PKP)，如果相等则U获得电子货币coin=(val,ω,μ,μ1,RO,R3,R4,R5,V)。

3.2.2离线支付阶段

1)顾客U把coin发给商家M。

2)商家M通过验证等式e(V,P)?=e(μ+hPKP,RO)e(μ1+hH1(ω,RO),PKO+PKP)来确定coin是否合法。如果等式不成立则M拒绝电子货币coin，如果等式成立则继续交易。

3)M随机选择一个c∈{0,1}*发给顾客U。

4)顾客计算(ζ,τ)给M,ζ=H3(coin‖c)，τ=r4+r3ζ。

5)当M收到(ζ,τ)，验证：ζ?=H3(val‖w‖μ‖μ1‖RO‖R3‖(τPKP-ζR3)‖R5‖c),如果等式成立，M接收离线电子货币(coin,ζ,τ,c)。

4　结语

本文研究分析了Chaudhry等提出的基于椭圆曲线认证加密的电子货币方案和Liu等提出的银行委托离线电子货币方案。利用椭圆曲线认证加密和双线性对，给出了两个改进的电子货币方案，使电子货币具有离线支付和二次花费追踪功能。理论分析表明，新方案中电子货币不可伪造，同时可以抵御重放攻击和假冒攻击，也可保证用户的匿名性和交易的公平性。在接下来的研究中，还需进一步完善所提方案的安全性，提高其效率，使得电子货币方案在电子支付中具有实用价值。

参考文献:

[1]CHAUM D. Blind signatures for untraceable payments [C]// CRYPTO 1983: Proceedings of the 1983 Workshop on the Theory and Application of Cryptographic Techniques. Boston: Springer, 1983: 199-203.

[2]CHAUM D, den BOER B, VAN HEYST E, et al. Efficient offline electronic checks [C]// EUROCRYPT 1989: Proceedings of the 1989 Workshop on the Theory and Application of Cryptographic Techniques, LNCS 434. Berlin: Springer, 1990: 294-301.

[3]CHAUM D, FIAT A, NAOR M. Untraceable electronic cash [C]// CRYPTO 1988: Proceedings of the 1988 Workshop on the Theory and Application of Cryptographic Techniques, LNCS 403. New York: Springer, 1990: 319-327.

[4]SHAMIR A. Identity-based cryptosystems and signature schemes [C]// CRYPTO 1984: Proceedings of the 1984 Workshop on the Theory and Application of Cryptographic Techniques, LNCS 196. Berlin: Springer, 1985: 47-53.

[5]AL-RIYAMI S S, PATERSON K G. Certificateless public key cryptography [C]// ASIACRYPT 2003: Proceedings of the 9th International Conference on the Theory and Application of Cryptology and Information Security, LNCS 2894. Berlin: Springer, 2003: 452-443.

[6]ABE M, FUJISAKI E. How to date blind signatures [C]// ASIACRYPT 1996: Proceedings of the 1996 International Conference on the Theory and Application of Cryptology and Information Security, LNCS 1163. Berlin: Springer, 1996: 244-251.

[7]ESLAMI Z, TALEBI M. A new untraceable off-line electronic cash system [J]. Electronic Commerce Research and Applications, 2011, 10(1): 59-66.

[8]LUO J N, YANG M H, HUANG S-Y. An unlinkable anonymous payment scheme based on near field communication [J].Computers and Electrical Engineering, 2016, 49: 198-206.

[9]YANG J-H, LIN P-Y. A mobile payment mechanism with anonymity for cloud computing [J]. Journal of Systems and Software, 2016, 116: 69-74.

[10]POURGHOMI P, SAEED M Q, GHINEA G. A secure cloud-based NFC mobile payment protocol [J]. International Journal of Advanced Computer Science and Application, 2014, 5(10): 24-31.

[11]YANG J-H, CHANG Y-F, CHEN Y-H. An efficient authenticated encryption scheme based on ecc and its application for electronic payment [J]. Information Technology And Control, 2013, 42(4): 315-324.

[12]CHAUDHRY S A, FARASH M S, NAQVI H, et al. A secure and efficient authenticated encryption for electronic payment systems using elliptic curve cryptography [J]. Electronic Commerce Research, 2016, 16(1): 113-139.

[13]LIU J H, HU Y.A new off-line electronic cash scheme for bank delegation [C]// ICIST 2015: Proceedings of the 5th International Conference on Information Science and Technology. Piscataway, NJ: IEEE, 2015: 186-191.