概率与统计一家亲

有关古典概型与统计相结合的题型是高考考查的一个重要题型,已成为高考命题的热点,真可谓“概率与统计一家亲”。下面举例说明。

例12016年某电视台问政直播节目首场内容是“让交通更顺畅”,A,B,C,D四个管理部门的负责人接受问政,分别负责问政A,B,C,D四个管理部门的现场市民代表(每一名代表只参加一个部门的问政)的人数的条形图如图1所示。

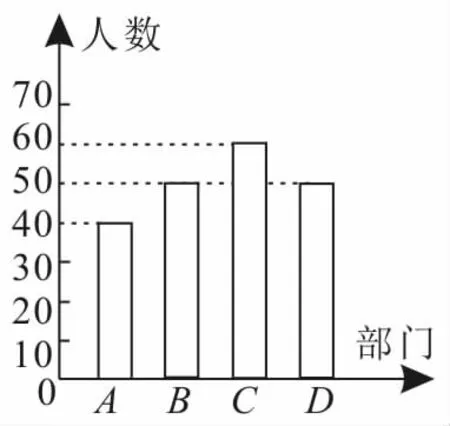
图1

为了解市民对实施“让交通更顺畅”几个月来的评价,先对每位现场市民进行了问卷调查,然后用分层抽样的方法从调查问卷中抽取20份进行统计,统计结果如表1所示。

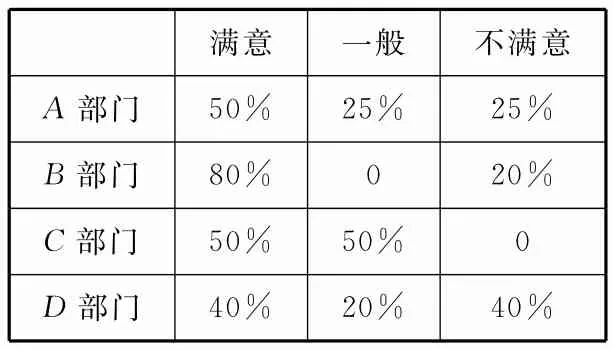
表1

(1)若现场市民甲选择的是A部门,求甲的调查问卷被选中的概率。

(2)若想从调查问卷被选中且填写不满意的现场市民中再选出2人进行电视访谈,求这2人中至少有1人选择的是D部门的概率。

分析：(1)从图1中找出分别负责问政A,B,C,D四个管理部门的现场市民代表的人数,便可求出甲的调查问卷被选中的概率。(2)按计算古典概型的三个步骤求解。

解：(1)由图1可得,分别负责问政A,B,C,D四个管理部门的现场市民代表共有200人,其中负责问政A部门的现场市民为40人。由分层抽样可得从选择A部门的调查问卷中抽取了设事件M为“现场市民甲的调查问卷被选中”,所以P(M)=由上述可得,若甲选择的是A部门,则甲的调查问卷被选中的概率是0.1。

(2)由表1可知,分别负责问政A,B,C,D四个部门的现场市民接受问卷调查的人数为4,5,6,5。其中不满意的人数分别为1,1,0,2。

记对A部门不满意的现场市民是a,对B部门不满意的现场市民是b,对D部门不满意的现场市民是c,d。设事件N为“从填写不满意的现场市民中选出2人,至少有1人选择的是D部门”。从填写不满意的现场市民中选出2人,共有(a,b),(a,c),(a,d), (b,c),(b,d),(c,d),即6个基本事件。而事件N有(a,c),(a,d),(b,c),(b,d),(c,d),即5个基本事件。所以故这2人中至少有1人选择的是D部门的概率是

例 2为了解学生身高情况,某校以10%的比例对全校700名学生按性别进行分层抽样调查,测得学生身高情况的统计图如图2,3所示。

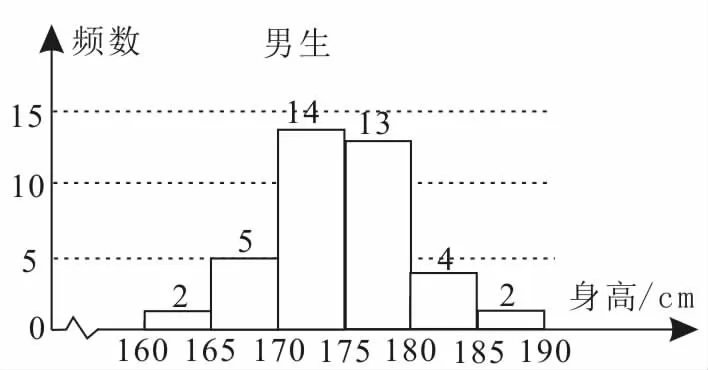
图2

图3

(1)估计该校男生的人数。

(2)估计该校学生身高在170～185cm之间的概率。

(3)从样本中身高在180～190cm之间的男生中任选2人,求至少有1人身高在185～190 cm之间的概率。

分析：(1)由样本中的男生人数可估计该校的男生人数。(2)由统计图计算该校学生身高在170～185cm之间的频率。(3)先计算样本中身高在180～190cm之间的男生人数和样本中身高在185～190cm之间的男生人数,进而按古典概型的计算方法来求至少有1人身高在185～190cm之间的概率。

解：(1)由图2和图3可知,样本中男生人数为40,女生人数为30,估计全校男生人数为400。

(2)由图2和图3知,样本中身高在170～185 cm之间的学生有14+13+4+3+ 1=35(人),而样本容量为70,所以样本中学生身高在170～185cm之间的频率为0.5。故由频率估计该校学生身高在170～185 cm之间的概率为0.5。

(3)样本中身高在180～185cm之间的男生有4人,设其编号为①②③④;样本中身高在185～190cm之间的男生有2人,设其编号为⑤⑥。从上述6人中任选2人的树状图如图4所示。

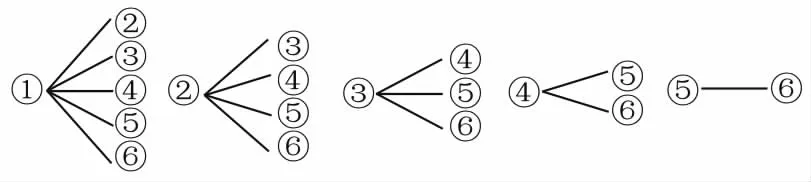
图4

故从样本中身高在180～190cm之间的男生中任选2人的所有可能结果数为15,至少有1人身高在185～190cm之间的所有可能结果数为9,因此,所求概率为