Rees矩阵半群的局部右正则性

罗肖强

0　引言

从20世纪20年代至今,很多国家的数学工作者通过各种途径研究Rees矩阵半群的相关问题,因为Rees矩阵半群具有非常完整的结构和稳定的性质,比如通过它等价地刻画了完全零单半群的结构和性质.Sushkevich最早研究Rees矩阵半群,1928年他在研究有限的单半群就开始涉及矩阵半群,得到了著名的Ress-Sushkevich定理,这个定理用群与集合来构造一个完全零单半群;当然这个定理的最完整的研究归功于Rees(1940).[1]具体的构造过程是:设S是一个完全单半群,(Ri)i∈I是一簇关于S的所有非零类,(Lλ)λ∈Λ是一簇关于S的所有非零类.为了不失一般性,令I=(S/).Hiλ=Ri∩Lλ是S的非零类,给定一个双射S→(I×G×Λ)∪{0},在(I×G×A)∪{0}中规定一个乘法运算.设G是一个群,I和Λ是一个非空集合,作一个映射P:Λ×I→G0,使得(Pλi)i∈I,λ∈Λ在S里,并且令

i,j∈I,g,h∈G0,λ,μ∈Λ规定乘法运算为(i,g,λ)(j,h,μ)=(i,g Pλjh,μ).显然乘法满足结合律,说明M0(G0;I;Λ;P)是一个半群;并且I×{0}×Λ是M(G0;I;Λ;P)的理想.称 M0(G0;I,Λ;P)为Rees矩阵半群,因夹集矩阵P而得名.[2]另外,容易得到:

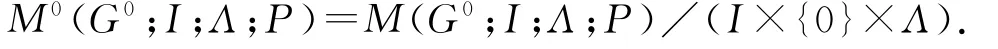
根据该等式.我们可以直接看出M0(G0;I;Λ;P)的元素是三元组(i,g,λ)的形式,且满足g≠0;当然,对于任意i和λ,零元我们常写成(i,0,λ).在本文中,我们假设G是一个半群,并给出一列半群局部右正则的概念,半群右正则表示与半群之间存在某些特殊的关系.鉴于如此,我们刻画了关于半群上Rees矩阵半群的相关新性质.[3-5]

在论文的第二部分给出了一列半群局部右正则的定义,根据定义证明了定理2.3对于任意的一半群上的任意一同余,那么它的一列商半群是局部右正则的;第三部分,第四部分证明了关于半群上Rees矩阵半群的相关性质.[2-3]

1　局部右正则

设S是一个半群,σ是S上的同余.记

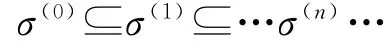
是S上的无限同余列,我们规定σ(0)=σ,特别地,对于任意的非负整数和任意的x∈S,若σ(n+1)是S上的同余关系,则a(σ(n+1))b当且仅当xa(σ(n+1))xb.[4]根据半群S上的右正则表示aρα,[5]我们令右正则表示的核为τ,设a,b∈S,对于任意的x,y∈S满足关系aτb⇔axτbx和yaτyb,即yaxτybx,由此说明τ是一同余关系.很显然,有τ(n)=ε(n+1),对于每个非负整数n,其中ε是S上的恒等关系.S/τ是一个商半群,[6-8]并且被叫着半群S上的右正则表示.半群右正则表示与半群之间存在某些特殊的关系,借助这种关系,我们研究Rees矩阵半群的局部正则问题.[4-5]设S是一半群,I和Λ是一非空集合,作一映射P:Λ×I→G0,使得(Pλi)i∈I,λ∈Λ属于S,规定乘法运算(i,g,λ)(j,h,μ)=(i,g Pλjh,μ),称 M0(G0;I;Λ;P)为Rees矩阵半群,简记为M(S;I;Λ;P).首先给出如下定义:

定义1.1 我们说一列半群S1,S2,…,Si…(i=1,2,…)是局部右正则的,如果对于每个正整数i,存在映射Pi+2,i+1:Si+2×Si+1→Si和映射Pi+1,i:Si+1×Si→Si+2使得

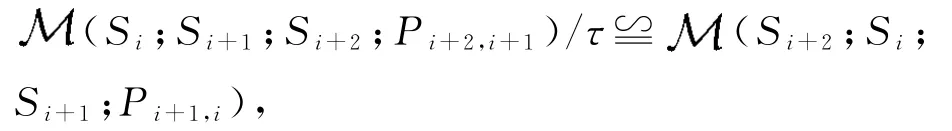
这就是说,半群Si上的Rees矩阵半群(Si;Si+1;Si+2;Pi+2,i+1)的右正则表示同构于半群Si+2上的Rees矩阵半群(Si+2;Si;Si+1;Pi+1,i)其中τ为右正则表示的核.

在此,我们给出这篇论文的主要定理之前,我们首先证明如下引理.

引理1.2 设S是任意一半群,i,j是任意的非负整数,σ是S上的同余,则

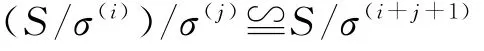
证明 我们先建立映射

当σ(i)⊆σ(i+j+1)时,ξi,j是一个被ξi,j∶aσ(i)aσ(i+j+1)完全确定的映射,很明显ξi,j是一满同态.我们容易证明ξi,j的核kerξi,j等于σs(j/σ)i,首先对于任意的a,b∈S,

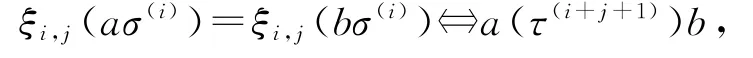
根据同态定理,有

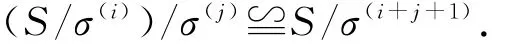
定理1.3 设S是任意一半群,σ是S上的任意同余,则这列商半群

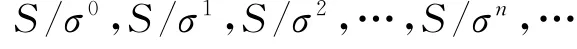
是局部右正则的.

证明 首先,我们考虑σ是恒等关系的情况.当σ0=ε和ε(n+1)=σ(n)(ε是恒等关系)时,对于每个非负整数n,证明这列商半群

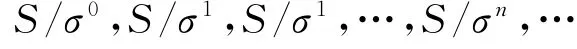
是局部右正则的.根据引理1.2,对于每一个半群和每一个非负整数n,有

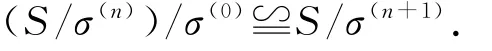
和

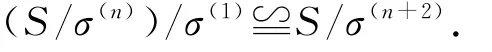
建立映射如下:

和映射

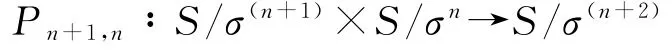
使得Rees矩阵半群

的右正则表示同构于半群S/σ(n+2)上的Rees矩阵半群

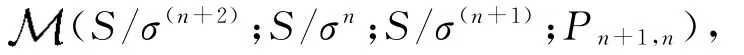
即

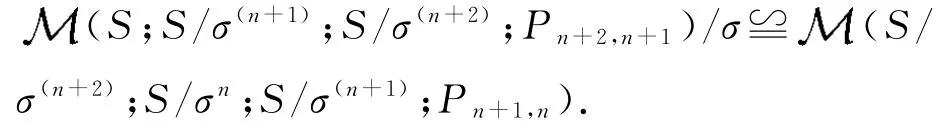
为了证明这个同构关系.我们设σ*是Rees矩阵半群

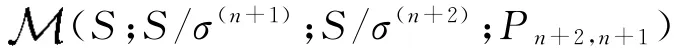
到它的右正则表示的典型同态核,φ是

随机选取首都医科大学2013级临床和基础医学等专业60名学生作为研究对象，将60名学生分为10个小组，每组5～7人。

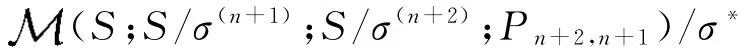
到

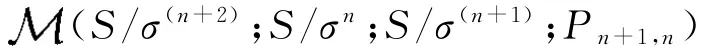
的映射.定义为

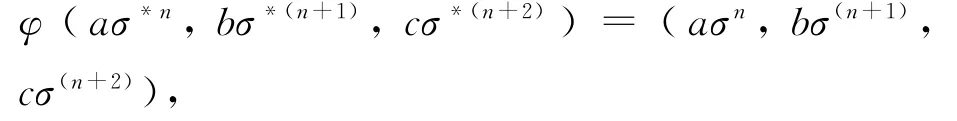
其中aσ*n,bσ*(n+1),cσ*(n+2)是σ*的同余类.显然φ是满的.现在我们证明φ是单的.假设

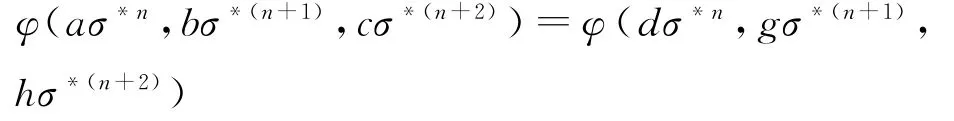
存在有

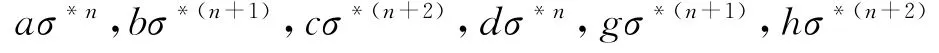
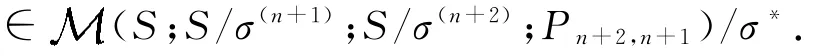
那么

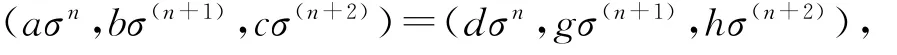
所以

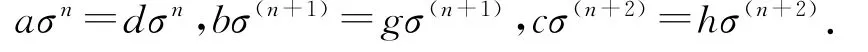
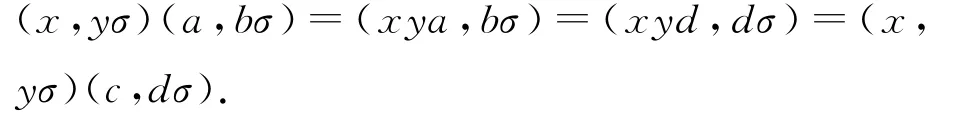
因此

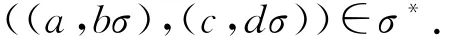
这就证明了φ是单射.因此φ是双射.对于φ是同态,这是显然的.故φ是Rees矩阵半群

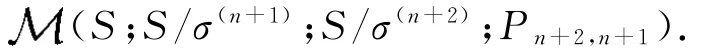
在半群S/σ(i+2)的右正则表示到Rees矩阵半群

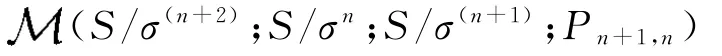
的一同构.接下来我们考虑σ是S上任意同余的情形.对于每一个非负整数n,我们考虑商半群S/σ(0)上的同余σ(n)/σ(0),[4]有σ(n)/σ(0)=ε(n)S/σ(0),故

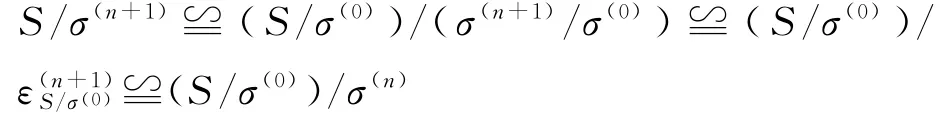
通过第一部分的证明,所以

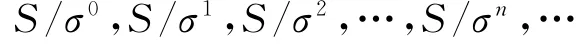
是局部右正则的.

2　遗传性质

这部分,根据半群常规性质,对于非负整数n,我们类推Rees矩阵半群

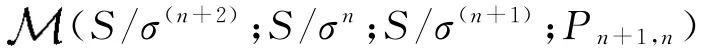
的一些结果

定理2.1 一个Rees矩阵半群

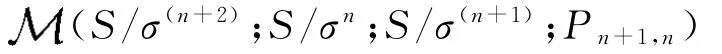
在S/σ(n+2)上是右单的充要条件是S/σ(n+2)是右单的,其中σ是半群S上的同余,n是非负整数,Pn+1,n∶S/σ(n+1)×S/σn→S/σ(n+2).

证明 假设S/σ(n+2)是右单的.设任意元素

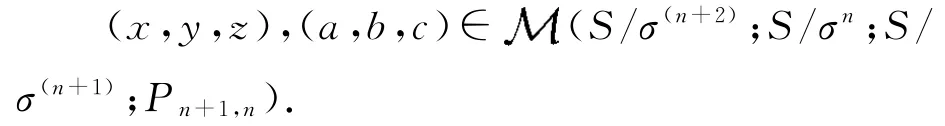
则有x PyzS/σ(n+2)=S/σ(n+2);对于任意的u∈S/σ(n+2)有x Pyzu=a.因此

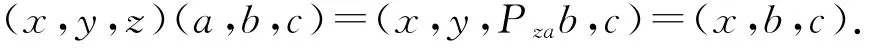
所以

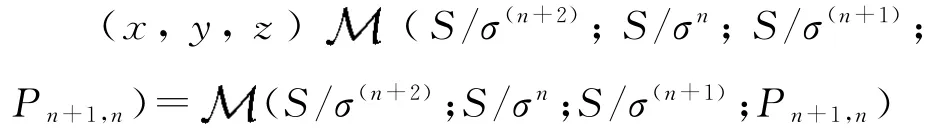
相反地,假设Rees矩阵半群

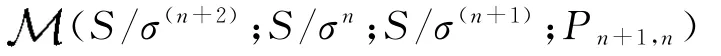
在S