压电陶瓷球形换能器耐电压与抗拉极限辐射声功率研究

赵勰



压电陶瓷球形换能器耐电压与抗拉极限辐射声功率研究

赵勰

(昆明船舶设备研究试验中心，云南昆明 650051)

对目前常用的压电陶瓷球形换能器辐射声功率进行研究，分别从压电陶瓷球振动时动态抗拉强度极限和退极化电压两方面分析其极限辐射声功率，两者中选择较小值，为极限辐射声功率计算提供部分技术指导；同时给定了特定尺寸下压电陶瓷球的宽带极限耐压辐射声功率，其结果可为球形换能器设计、使用提供参考。

压电陶瓷球；抗拉强度极限；退极化电压；声功率

0 引言

声波是目前人类发现的能在水中远距离传播的最有效载体，但相对而言，由于海水的声吸收和声波的扩散损失等，其传播距离有限，尤其高频传输时，传播距离更短。因此科研人员在进行声源研究时，为了获得远距离传输，一般在降低辐射频率的同时尽可能地提高声源的辐射声功率，即提高换能器两端的电压。但换能器最大辐射声功率是有限的，其大小与换能器的尺寸与材料有关。球形压电换能器的辐射声功率主要由压电陶瓷球的直径、壁厚以及材料特性等决定。如果无限制地提高换能器两端的电压，换能器就会损坏，表现为换能器辐射声功率的严重下降或性能指标的变化，这主要是由于压电陶瓷退极化或破裂引起。如典型的钛酸钡压电陶瓷，室温情况下，在400 V/mm(有效值)的电场作用下开始有明显的退极化，到800 V/mm(有效值)时基本已完全退极化[1]；锆钛酸铅压电陶瓷中的PZT-4材料，其交流退极化场约为350 V/mm(有效值)。此外，即使未达到退极化程度，当压电瓷机械交变应力超过某一值时，材料就要破裂，即使低于此值，应变的反复变化也会导致机械疲劳[2]。陶瓷的额定动态抗张强度规定了在交变应力作用下不发生断裂和机械疲劳的上限值。不同材料额定动态抗张强度不同，最大辐射声功率也不同，而且额定动态抗张强度与换能器的辐射声功率有着直接关系。此外，在工程应用时，为了使用便捷，往往用一个特定尺寸的压电陶瓷球在很宽的频带内实现发射，此时一般是通过提高陶瓷球两极的电压实现大功率的目的，很容易出现退极化现象，尤其在低频段，退极化现象更严重。本文主要解决上述问题。

1 辐射声功率计算

1.1 耐压辐射声功率计算

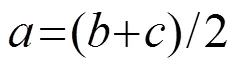
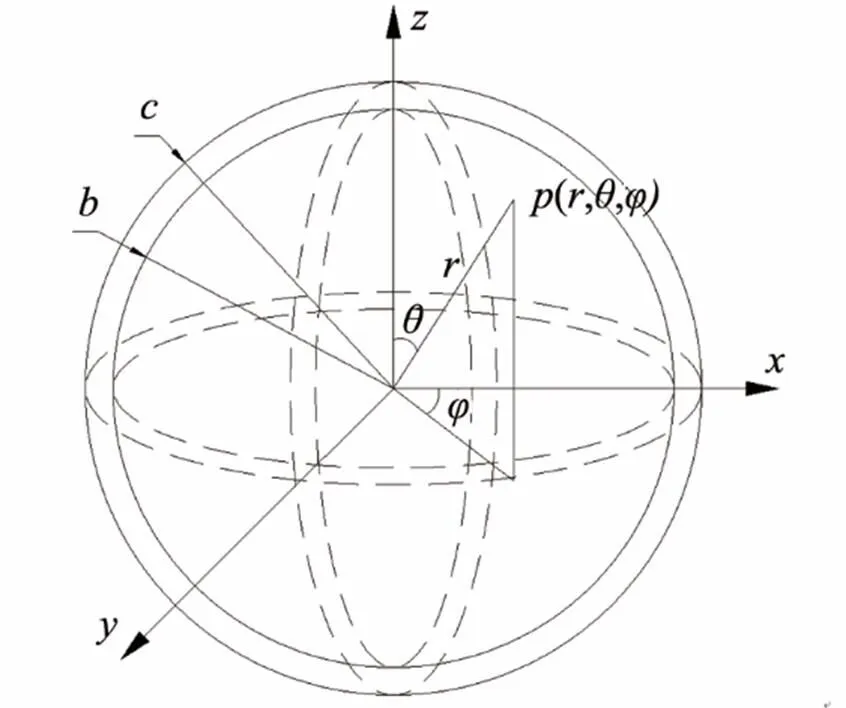
图1 压电陶瓷球分析模型

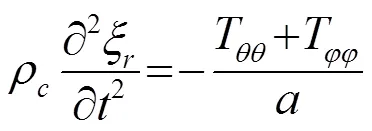
当陶瓷球作简谐振动时，则

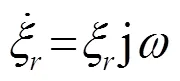
将式(2)代入式(1)，并简化得

根据球壳的工作状态，球壳振动的压电方程可简化为

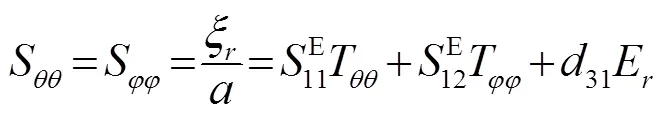
根据式(6)可得球壳在振动时的交变电量为

所以，球壳上的电流为

式中：为球壳内外表面电压。

将式(3)与式(4)代入式(8)，化简得

图2 水中球形压电陶瓷换能器等效电路图

根据水中等效电路图，结合空气中的振动特性，压电陶瓷球的辐射声功率为

从式(10)可知，换能器要实现谐振，需要满足

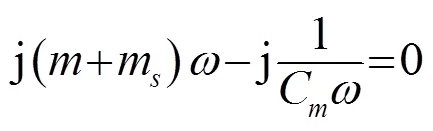
因此，陶瓷球在水下的谐振频率为

利用图2还可以求出：

1.2 抗拉辐射声功率计算

以陶瓷球的球心为原点，建立球坐标系，则在该坐标系中的某点处的声压可表示为

水中质点的运动方程为

式中：为质点振速。

将式(15)代入式(16)，得：

将式(17)代入式(18)，可求得待定系数：

将式(19)代入式(15)，声压可表达为

声场强度为

将式(19)与式(20)代入式(21)，得

因为以声源为球心的球面上声波强度相等，所以在以为半径的球面上的功率为

2 最大辐射功率

式(13)已经给出了压电陶瓷球在给定电压情况下的谐振辐射声功率。由于压电陶瓷薄壳球两个电极间的耐压是有限的，当达到极限时陶瓷球会出现退极化现象，因此知道退极化电压即可计算出该压电陶瓷球形换能器在谐振频率附近耐电压最大辐射声功率。

综合式(13)与式(24)，取两者的最小值即为压电陶瓷薄壳球形换能器在谐振频率附近的最大辐射声功率。

以厚度为2 mm的压电陶瓷球为例，陶瓷球材料为PZT-4型，根据式(13)与式(24)得出不同尺寸陶瓷球在谐振频率附近的最大辐射声功率，如图3所示。根据水声工程中发射换能器辐射声功率的计算方法，图3中分析声功率时，以声压级表述。从图3可看出，2 mm壁厚的压电陶瓷球在36.2 kHz时，其耐压极限辐射声功率与抗拉极限声功率相等，当小于此频率时，其参考极限辐射声功率主要由陶瓷球的退极化电压决定，反之则由陶瓷材料的抗拉强度决定。

图3 从耐电压和抗拉伸确定的极限辐射声功率图

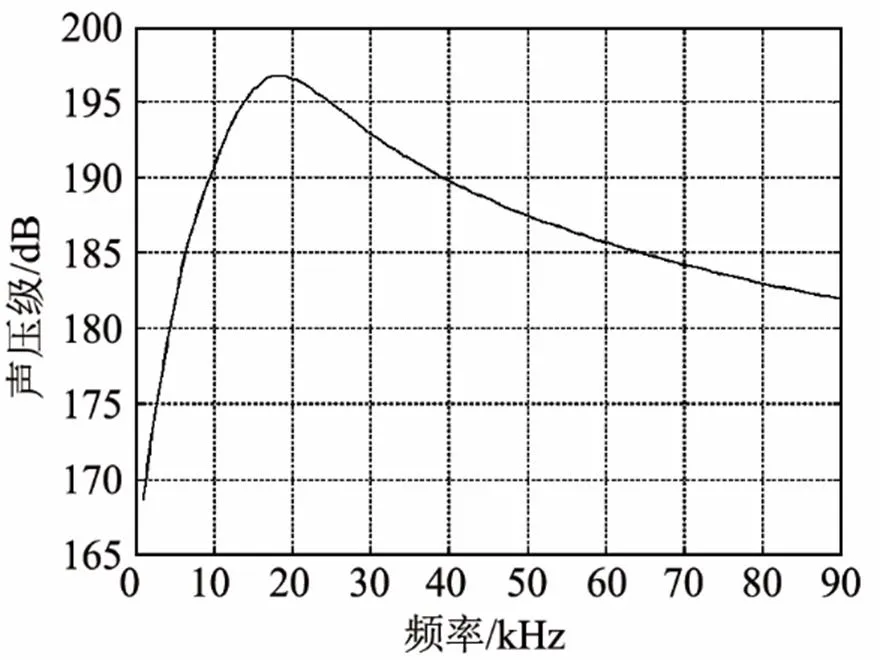
图4 特定尺寸陶瓷球极限辐射声功率图

3 总结

本文分别从压电陶瓷球振动时动态抗拉强度极限和退极化电压两方面分析其极限辐射声功率，得出理论公式。根据谐振频点，两者中选择较小值作为其实际谐振工况下的参考极限辐射声功率。通过计算某一壁厚的PZT-4压电陶瓷球在10～90 kHz范围内谐振工况下的耐电压与抗拉极限辐射声功率，得出低于某一频率时，球形换能器参考极限辐射声功率主要由陶瓷球的退极化电压决定，反之则由陶瓷材料的抗拉强度决定。并且在由退极化电压决定辐射声功率的低频段，给出了特定尺寸压电陶瓷球的全频带极限辐射声功率，结果可为球形换能器宽带设计与使用提供部分技术指导。由于压电陶瓷生产厂家工艺的不同以及陶瓷之间的个性差异，建议在设计压电陶瓷球换能器时取一个0.9的安全系数。

[1] 栾桂冬, 张金铎, 王仁乾. 压电换能器和换能器阵[M]. 北京: 北京大学出版社, 2005:81. LUAN Guidong, ZHANG Jinduo, WANG Renqian. Piczoelectric transducers and arrays[M]. Beijing: Peking University Press, 2005, 81.

[2] 许光, 吴培荣, 刘振君. 高频换能器功率疲劳分析[J]. 声学技术, 2015, 34(3): 283-286. XU Guang, WU Peirong, LIU Zhenjun. Research on the power fatigue problem of high frequency underwater transducer[J]. Technical Acoustics, 2015, 34(3): 283-286.

[3] 何祚镛, 赵玉芳. 声学理论基础[M]. 北京: 国防工业出版社, 1981: 85-86. HE Zuoyong, ZHAO Yufang. Base theory of sound[M]. Beijing: National Defense Industry Press, 1981: 85-86.

[4] 王荣津. 水声材料手册[M]. 北京: 科学出版社, 1983: 142-150. WANG Rongjin. Handbook for underwater acoustic materials[M]. Beijing: Science Press, 1983: 142-150.

A study of the maximum radiated sound power of spherical piezoelectric ceramic transducer constrained by depolarization voltage and ultimate tensile strength

ZHAO Xie

(Kunming Shipborne Equipment Reseach and Test Center,Kunming 650001, Yunnan, China)

This paper researches the problem of the sound power radiated by spherical piezoelectric ceramic transducer, analyzes the maximum radiated sound power from the two aspects of ultimate tensile strength and depolarization voltage and chooses the smaller value between the twofor practical uses, which can provide some technical guidance for the calculation of utimate radiated sound power.At the same time, the broadband sound power radiated by the piezoelectric ceramic ball with specific size under ultimate voltage is given; this result can provide a reference for the spherical transducer design.

piezoelectric ceramic ball; utimate tensile strength; depolarization voltage; sound power

TB561

A

1000-3630(2018)-01-0094-04

10.16300/j.cnki.1000-3630.2018.01.017

2017-04-12;

2017-08-13

赵勰(1982－), 男, 陕西榆林人, 硕士, 高级工程师, 研究方向为水声换能器。

赵勰, E-mail: zhaoxie750@163.com