Direction-of-arrival estimation of near-field sources based on compressed symmetric nested array and sparse signal reconstruction
LI Shuang, ZHENG Da-qing, LIU Wei, HU Shun-ren, HE Wei
Direction-of-arrival estimation of near-field sources based on compressed symmetric nested array and sparse signal reconstruction
LI Shuang1, ZHENG Da-qing1, LIU Wei1, HU Shun-ren1, HE Wei2
(1. School of Electrical and Electronic Engineering, Chongqing University of Technology, Chongqing 400054, China;2. Key Labarotory of Wireless Sensor Networks and Communication, Shanghai Institute of Microsystem and Information Technology, Chinese Academy of Sciences,Shanghai 200180, China)
In this paper, a novel underdetermined direction-of-arrival (DOA) estimation method based on compressed symmetric nested array and sparse signal representation is proposed in the near-field. Firstly, the forth order cumulants are employed to transform the original two-dimensional parameter estimation problem into a one-dimensional one and to obtain the difference co-array of the physical array. Then, in order to further increase the angular resolution and reduce the estimate error, the received signals of the virtual array are sparsely represented in spatial domain. Finally, the DOAs of the sources are founded through the use of the L1-regularized least square method. Compared to the existing methods, the proposed approach can process more sources and have lower variance and higher resolution. Simulation results are given to demonstrate the effectiveness and efficiency of the proposed method.
array signal processing; underdetermined direction-of-arrival estimation; near-field; sparse signal recovery; fourth order cumulant
0 Introduction
Source localization using sensor arrays plays an important role in many applications such as radar, sonar, wireless sensor networks, wireless communication and so on. According to the distance between the sources and the reference sensor of an array, source localization can be categorized into two types: far-field and near-field. In the far-field, the signal at the array can be approximated as plane wave and only the direction-of-arrival (DOA) estimation is required. However, the wavefront of the signal must be characterized by both azimuth and range in the near-field, where a joint azimuth and range estimation should be conducted. Therefore, the performances of those source localization methods making a far-field assumption will severely degrade in the near-field.

In this paper, based on compressed symmetric nested array and sparse signal reconstruction, a new source localization method is proposed in the near-field. The degrees of freedom are further increased by exploiting sparse signal reconstruction so that higher resolution can be achieved. Compared to the existing methods, the proposed method has a superior performance including higher resolution and lower variance.
The rest of the paper is organized as follows. Section 2 describes the DOA estimation model in the near-field. How the proposed method works is given in Section 3, which is followed by simulation results in section 4. Section 5 concludes the paper.
1 Data model


where denotes the source, represents the noise received by thesensor, refers to the wavelength of the sources, denotes the number of snapshots, stands for the distance between the source and the reference sensor of the array and is the distance from the sensor to the source.
According to Fig.1, we have
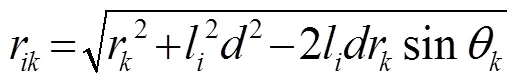
Through the use of second order Taylor expansion of (2), we can obtain the so-called Fresnel approximation
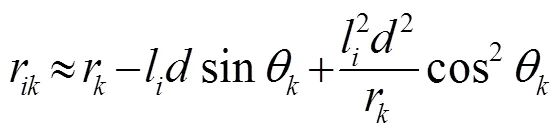
Substituting (3) into (1), we obtain

where
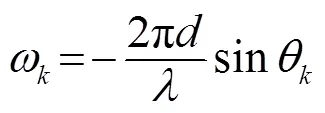
and



To simplify the derivation, we make some assumptions as follows.
(A1) - the sources are non-Gaussian, and independent with each other.
(A2) - the noises are Gaussian, either white or colored.
(A3) - the noises are independent of the sources; and
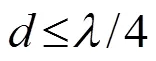
2 The proposed method
2.1 Nested array and compressed symmetric nested array(CSNA)

Fig.2 Nested array and compressed symmetric nested array
2.2 The proposed method
To acquire the difference co-array of a physical array, we exploit the fourth order cumulants of the received signals, which can be defined as
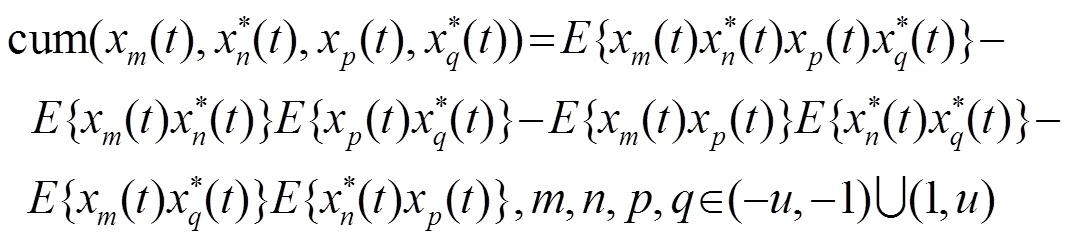
Under the assumptions (A2) and (A3), by substituting (4) into (8) and employing the properties of cumulants, we have.
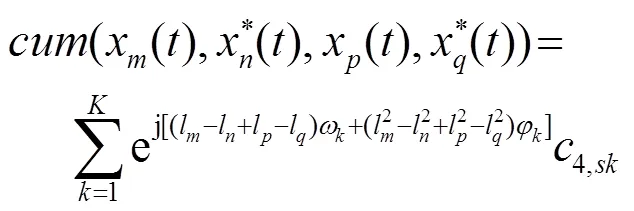





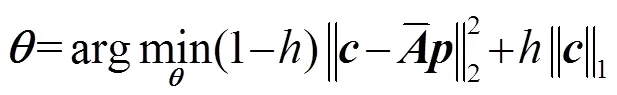
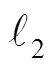

1: regarding the number of sources that the proposed method can process, we give a theorem to explain it.


3:As to array geometry, since the proposed method only requires the array is symmetric, it will work well when the number of the array is odd as we mentioned before.
3 Simulation results
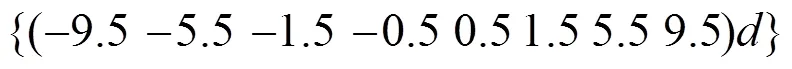
3.1 Spatial spectra


Hence, according to the two figures, we can draw a conclusion that our method achieves higher resolution compared to the other two methods, which will be verified in the subsequent section. Besides, both the proposed method and the method in[13] can identify more sources than sensors.
3.2 RMSE
In this subsection, the RMSE of the above three methods are evaluated. The RMSE is defined as
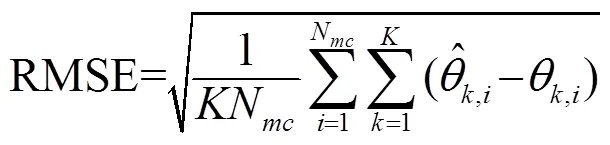
wheredenotes the number of Monte Carlo trials, and represent theestimate and real DOA in the run, respectively.

Fig.4 Angular spatial spectrum for underdetermined case
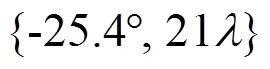
Then we keep all the parameters the same as the last experiment except that the SNR is fixed 10dB and make a comparison to the three methods when the number of snapshots ranges from 200 to 4 000. Fig.6 illustrates RMSE of the three methods with respect to the number of snapshots. It can be noted that the proposed method has a higher RMSE when the number of snapshot is relatively small while lower variance can be obtained by the proposed method when a great number of snapshots are available compared to the other methods.

Fig.5 RMSE versus SNR

Fig.6 RMSE as a function of the number of snapshot
3.3 Resolution

Then, the resolution probabilities of the three methods are investigated for different numbers of snapshots, which varies from 200 to 2 000 with a step of 300. How the resolution ability changing with the number of snapshots is exhibited in Fig.8. It can be obviously noted that the proposed method outperforms the other two methods.
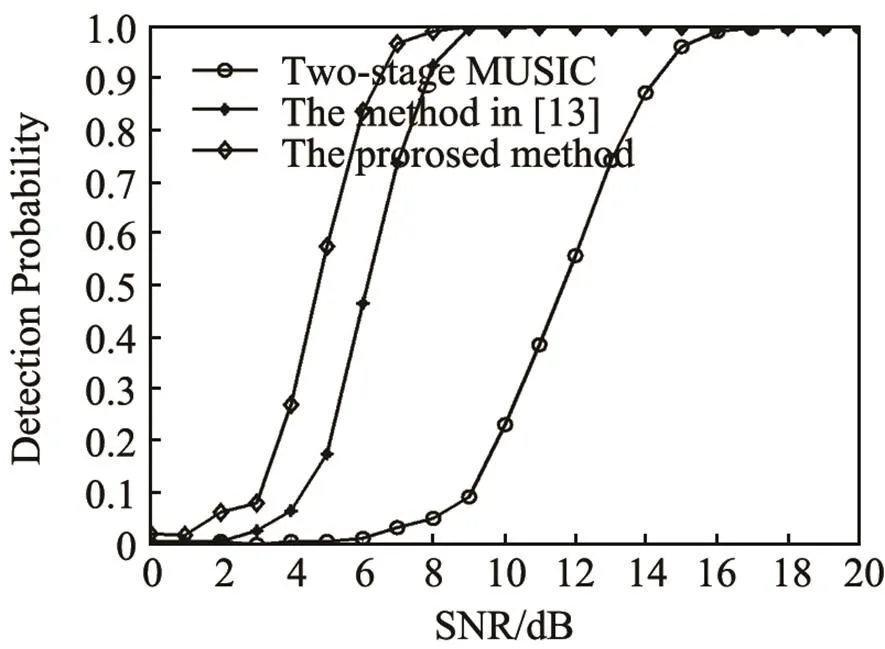
Fig.7 Resolution ability with respect to SNR

Fig.8 Resolution ability with respect to the number of snapshots
4 Conclusions
In this paper, a novel DOA estimation method based on compressed symmetric nested array and sparse signal recovery is proposed in the near-field. The proposed method has several advantages. First, it can process more sources than sensors. Furthermore, compared to the existing methods, the proposed method can obtain higher resolution and lower variance. Future research will involve the design of more efficient array for near-field source localization.
[1] ZHI W, CHIA M W. Near-field source localization via symmetric subarrays[C]//2007. IEEE International Conference on Acoustics, Speech and Signal Processing(ICASSP 2007) IEEE, 2007: 1121-1124.
[2] XIE J, TAO H, RAO X, et al. Comments on “near-field source localization via symmetric subarrays”[J]. IEEE Signal Processing Letters, 20155(22): 643-644.
[3] LIANG J, LIU D. Passive localization of mixed near-field and far-field sources using two-stage MUSIC algorithm[J]. IEEE Transactions on Signal Processing, 201058(1): 108-120.
[4] MALIOUTOV D, ÇETIN M, WILLSKY A S. A sparse signal reconstruction perspective for source localization with sensor arrays[J]. IEEE Transactions on Signal Processing, 200553(8): 3010-3022.
[5] TIAN Y, SUN X. Passive localization of mixed sources jointly using MUSIC and sparse signal reconstruction[J]. AEU- International Journal of Electronics and Communications, 201468(6): 534-539.
[6] HU K, CHEPURI S P, LEUS G. Near-field source localization using sparse recovery techniques[C]//Signal Processing and Communications (SPCOM), 2014 International Conference on IEEE, 2014: 1-5.
[7] WANG B, LIU J, SUN X. Mixed sources localization based on sparse signal reconstruction[J]. IEEE Signal Processing Letters, 201219(8): 487-490.
[8] 李双, 刘骁, 胡顺仁, 等. 对称子阵列的近场信号稀疏表示定位方法[J]. 信号处理, 2017, 33(1): 78-86.LI Shuang, LIU xiao, HU Shunren. et al. Localization of near- field sources using the sparse signal representation with symmetric subarrays[J]. Journal of Signal Processing, 201733(1): 78-86.
[9] 李双, 刘骁, 胡顺仁, 等. 加权稀疏信号重构的近场源定位方法[J]. 声学技术, 2017, 36(1): 75-80. LI Shuang, LIU Xiao, HU Shunren, et al. Source localization based on sparse signal recovery using a weighted penalty in the near-field[J]. Technical Acoustics, 2017, 36 (1): 75-80.
[10] 刘亮, 陶建武, 黄家才. 基于稀疏对称阵列的近场源定位[J]. 电子学报, 2009, 37(6): 1307-1312. LIU Liang, TAO Jianwu, HUANG Jiacai. Near-field source localization based on sparse symmetric array[J]. Acta Elctrnica Sinica, 200937(6): 1307-1312.
[11] 梁国龙, 韩博. 基于互素对称阵的近场源定位[J]. 电子与信息学报, 2014, 1(1): 135-139. LIANG Guolong, HAN Bo. Near-field sources localization based on co-prime symmetric array[J]. Journal of Electronics & Information Technology, 20141(1): 135-139.
[12] PAL P, VAIDYANATHAN P. Nested arrays: a novel approach to array processing with enhanced degrees of freedom[J]. IEEE Transactions on Signal Processing, 201058(8): 4167-4181.
[13] LI S, XIE D. Compressed symmetric nested arrays and their application for direction-of-arrival estimation of near-field sources[J]. Sensors, 201616(11): 1939.
[14] GRANT M, BOYD S, YE Y. CVX: Matlab software for disciplined convex programming. Available: http://cvxr. com/ cvx/. 2008.
[15] LI S, JIANG X, MA S, et al., Sparse cumulants fitting for direction-of-arrival estimation without redundancy[J]. International Journal of Antennas and Propagation, 2013(3): 1-7.
压缩对称嵌套阵列和稀疏信号重构的近场目标方位估计
李双1,郑大青1,刘伟1,胡顺仁1,何为2
(1. 重庆理工大学电气与电子工程学院,重庆 400054; 2.中国科学院上海微系统与信息技术研究所无线传感网与通信重点实验室,上海 200180)
针对现有近场源估计算法中近场源数量受限于阵元数的问题,提出了一种基于稀疏对称嵌套阵列和稀疏信号重构的近场欠定波达方向估计方法。首先利用四阶累积量,将二维空间参数估计问题转化为一维参数估计问题,同时得到差分阵列;为了进一步提高估计分辨率与减少估计误差,对虚拟阵列的接收信号在空间域进行稀疏表示;最后通过L1范数最小二乘法得到目标源的波达方向。相较于现有算法,该方法可以估计更多的目标源,并且有更低的均方误差与更高的分辨率。实验仿真验证了算法的有效性与优越性。
阵列信号处理;欠定波达方向估计;近场;稀疏信号重构;四阶累积量
TN911.72
A
1000-3630(2018)-01-0082-07
10.16300/j.cnki.1000-3630.2018.01.015
2017-03-17;
2017-05-03
重庆市基础与前沿研究计划项目(cstc2015jcyjA040055); 重庆市教委科学技术研究项目(KJ1500917, KJ1600936)
李双(1986-), 男, 四川南充人, 博士, 讲师, 研究方向为阵列信号处理及其应用。
李双, E-mail: lis@cqut.edu.cn

