基于声场特性研究的汽车空气滤清器噪声优化

袁守利，王　鑫，刘志恩

(1.武汉理工大学 现代汽车零部件技术湖北省重点试验室,湖北 武汉 430070；2.武汉理工大学 汽车零部件技术湖北省协同创新中心，湖北 武汉 430070)

进气系统的噪声是汽车最主要的噪声源之一。进气系统的噪声主要是指进气口处的噪声，这个噪声源距离车厢的距离很近，因此对车内噪声的贡献非常大。同时，进气口噪声也是汽车最主要的通过噪声源。

在进气系统中，空气滤清器的作用不止清洁空气，同时它相当于扩张腔，其声学特性对进气噪声有重要影响。在进气管结构不易改变的前提下，对空气滤清器的结构进行优化是改善进气噪声简洁且有效的办法。由于空气滤清器尺寸较大，且形状一般不规则，用一维平面波理论计算误差较大，逐渐被三维有限元法和边界元法取代，且三维计算方法在低频段的计算结果具有很好的准确性。文献[1]利用边界元法求解频率响应特性，并对空气滤清器的消声特性进行了计算分析，在传递损失计算的基础上对空气滤清器的声学特性进行了改进设计。文献[2]针对点火频率引起空气滤清器进气噪声中的低频峰值,采用边界元法对改进设计的空气滤清器系统进行了低频消声性能的研究，在1～1 000 Hz频率范围内，分析了旁通管和共振腔的消声作用。文献[3]对比了边界元法、有限元法和一维有限体积法在分析进气系统声学性能时的优劣性，指出边界元法和有限元法比一维有限体积法具有更高的准确性，并分析了有限元法用于预测滤芯消声性能的可行性。文献[4]分别采用流体动力学仿真和有限元方法对空气滤清器的流阻和降噪能力进行了计算，根据试验测得噪声特性，对空气滤清器进行降噪优化，并重新计算优化后空气滤清器的流动阻力和消声量。

下面采用有限元分析方法在声学三维计算软件Virtual Lab和一维计算软件GT-Power中对空气滤清器模型进行仿真，对其结构进行优化后，再次进行声学性能仿真验证，最后进行试验验证。

1　某乘用车发动机进气噪声频率特性

进气噪声主要是进气时管道内压力波动产生的谐波低频脉动噪声[5]，其谐波频率为：

(1)

式中：i为气缸数;n为转速；τ为冲程系数,4冲程τ= 2，2冲程τ= 1；k为谐波次数。f1为基频，高谐次fk的强度大大减弱，进气噪声主要以1 000 Hz以下的中低频成分为主。

在对进气系统进行结构优化之前先进行摸底试验，借助隔音措施将进气系统引出机舱外，以期提取纯粹的进气管口噪声，为后续噪声优化提供依据。试验在整车半消声室中进行，试验工况为三档发动机节气门全开急加速工况。试验现场如图1所示。

图1　整车半消声室试验现场

4缸发动机中2/4/6/8阶噪声是研究进气的主要噪声。图2和图3是该发动机在试验工况下进气口噪声声压(级)和频谱图，根据摸底试验各个测试状态结果对比分析得出：进气系统噪声成分以2阶及谐阶次为主，同时存在宽频噪声；现有进气系统对阶次成分消声能力较强。

图2　进气口噪声各谐阶

图3　进气口处噪声频谱图

试验进行了进气系统有无空气滤清器的进气管口噪声的测试，根据测试结果分析出空气滤清器对进气噪声的贡献量以及特征频率，如图4所示。结果说明空气滤清器对进气噪声产生了宽频噪声，频率范围为230～770 Hz、840～1 320 Hz。

通过图2和图3的对比，重点增大空气滤清器中低频段(50～1 000 Hz)的消声能力，重点针对73 Hz、183 Hz、375 Hz和470 Hz问题频率优化结构，并减少高频段的宽频噪声。

图4　空气滤清器频谱图

2　空气滤清器结构改进设计与仿真

为减少仿真分析的工作量，先对几何模型进行几何清理，根据声学仿真1/6波长原理和流体仿真对网格的要求，在Hypermesh前处理软件中进行四面体网格划分，而后分别将网格文件导出声学和流体分析对应的文件格式，再继续下一步的分析。划分完网格的空气滤清器的有限元模型共生成18 398个网格，节点9 201个。图5为空气滤清器有限元模型。

图5　空气滤清器有限元模型

2.1　原模型的声学仿真分析

空气滤清器的声学性能计算类似于消声器，一般采用有限元法或边界元法[6]。有限元法预测空气滤清器的消声特性广泛应用于声学元件传递损失的计算。传递损失能真实反映消声元件的固有消声特性，常用来评价消声元件。传声损失TL,也称传递损失,或透射损失,定义为消声结构进口的噪声能量(入射声能)与出口能量(透射声能)之差，其计算公式如下：

(2)

式中：pi为进口入射声波声压;po为空气滤清器出口入射声压;Si为进口截面积;So为出口截面积;ρ为大气密度;c为当地声速。传声损失的定义是消声结构对声能量衰减,能量传播具有方向性使传声损失测量过程比较复杂。在实际运用中通常将传声损失定义为进出口的声压级差。

TL=Lpi-Lpo

TL=20lg(pi/po)

(3)

这样的定义既便于试验研究也能反映消声结构的声学特性。

本文采用了一维和三维两种计算方法来对比分析建模的正确性。

首先采用试验设备阻抗管对原空气滤清器进行了传递损失的试验[7]，实验原理用传递矩阵法在阻抗管内测量试件的法向入射传声损失。在传声器1和传声器2的位置上测量声压，求得两个传声器信号的声压传递函数；同样，在传声器3和传声器4的位置上测量声压，求得两个传声器信号的声压传递函数。由传递矩阵法计算试件的法向入射传递损失。测量装置示意图如图6所示。

图6　测量装置示意图

一维计算过程是在GT-Power中进行传递损失的计算。三维计算过程是从Hypermesh软件中导出bdf文件，在Virtual Lab中进行传递损失的计算。由于是初步研究空气滤清器的低频消声性能，并不考虑平均流和湍流的影响，因此在无流动的静态条件下分析其声学特性。将空气滤清器模型的流体运动出口截面作为声源入口，加载单位振动速度，空气滤清器进口处根据圆形平面活塞辐射假设，在入口截面设定阻抗值。计算得到空气滤清器在0～2 000 Hz的传递损失，频率间隔为1 Hz。

试验与两种计算结果的对比如图7所示。

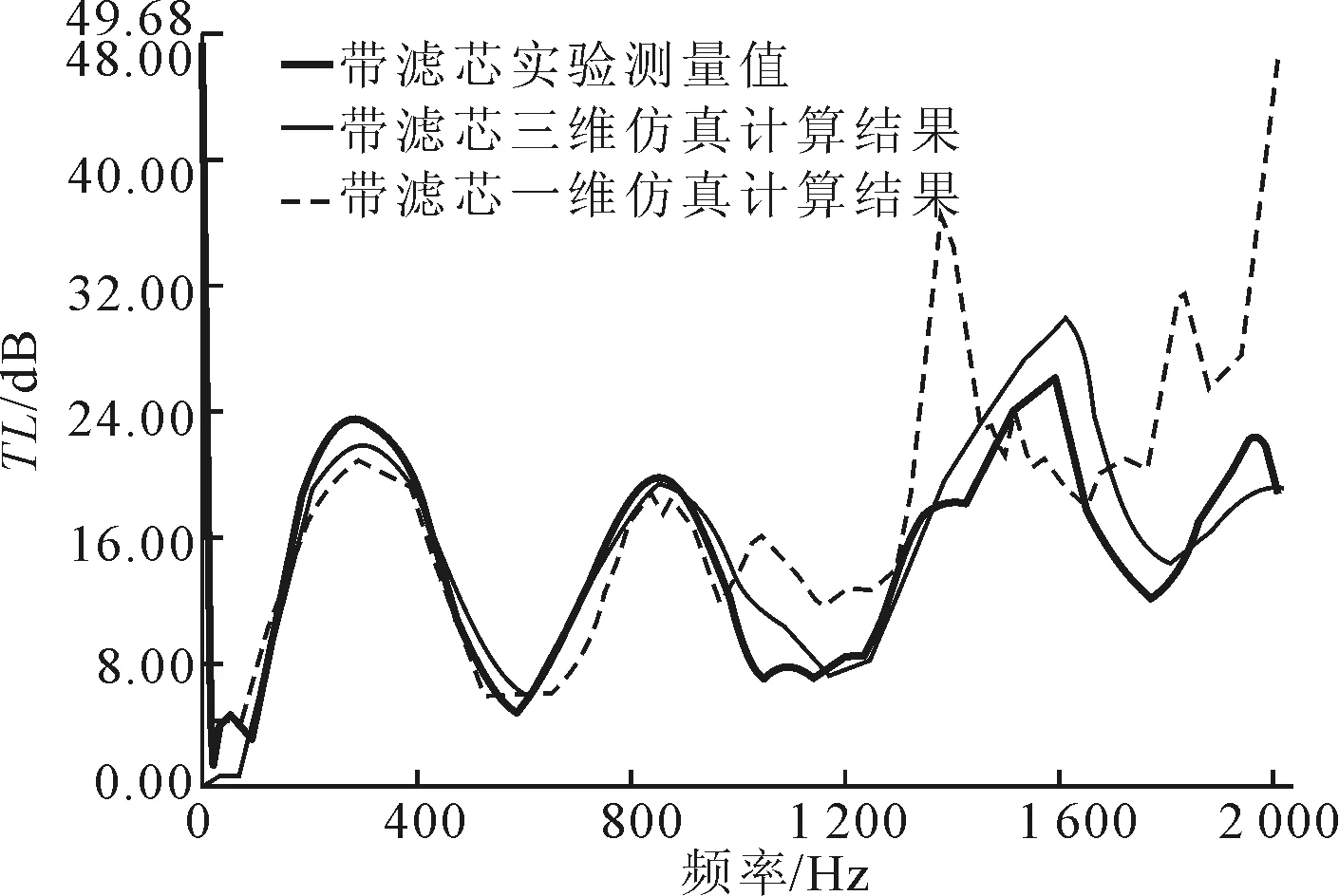
图7　空气滤清器TL结果对比

对比分析一维和三维的仿真计算结果可知，在1 000 Hz以下时，一维和三维仿真计算都可以较为准确地得到空气滤清器的传递损失；相对而言，三维仿真方法在1 000 Hz以上时也有较高的准确性。空气滤清器传递损失三维计算曲线与试验曲线有较高的吻合度，在1 300 Hz以上时幅值存在波动，可能是高次波的影响，使得基于平面波理论计算的幅值有所偏差。因此，在低频段，一维仿真分析准确率也较高，求解速度快，模型修正简便，后续的验证分析将采用一维方法。

2.2　改进的空气滤清器声学特性计算

进气系统低频噪声可以通过赫姆霍兹谐振腔、1/4波长管进行消声，谐振腔一般用于消除频率较低的噪声[8]，其消声频率为：

(4)

式中:c为声速;s为连接谐振腔管道的截面积;lk为连接管道的等效长度;V为谐振腔的体积。1/4 波长管是安装在主管道上的一个封闭的管子，通常用来消除频率较高的噪声。1/4 波长管理论消声频率为：

f=c/(4L)

(5)

式中:L为1/4波长管的长度。

宽频噪声通过安装宽频共振器来进行减弱。赫姆霍兹共振腔的单频和带宽集中的频率特点可以改进空气滤清器的声学特性，还可以对进气噪声的低频成分起到消声作用[9]。因此对原模型进行结构优化，增加4个谐振腔(各部分结构对应的消声频率在图8中标示)和一个1/4波长管，另外再增加一个宽频共振器减弱空气滤清器产生的宽频带噪声。优化后的结构如图8所示。

图8　优化后的空气滤清器模型

为了验证优化后的空气滤清器能够满足要求，重新进行声学性能计算，如图9所示。

图9　改进后的空气滤清器声学性能计算结果

图9(a)是采用GT-Power仿真得到的改进后的进气管口噪声曲线与原模型和目标线的对比，可以看出整个转速范围进气噪声均在目标线以下。从图9(b)的传递损失图上可以看出改进后空气滤清器的传递损失在对应频段均出现峰值，其中350 Hz频段传递损失出现较高峰值且频带较宽；在73 Hz频率也出现明显峰值，其它对应消音元件均出现对应峰值。采用GT分析模型计算进气系统背压为3.1 kPa，小于原进气系统3.4 kPa，满足降噪要求。

3　空气滤清器优化后的进气噪声试验

根据改进后的几何模型对实际空气滤清器进

行改进，并加工出样件，如图10所示。

图10　优化后的空气滤清器

采用上文描述的试验方法重新对改进模型进行了进气噪声试验，由于需要重新与原模型测试结果重新对比，由于测试环境的差异可能导致第二次的测试结果有差异，因此需要对原模型重新进行试验，以便与改进模型进行对比，试验结果如图11所示。

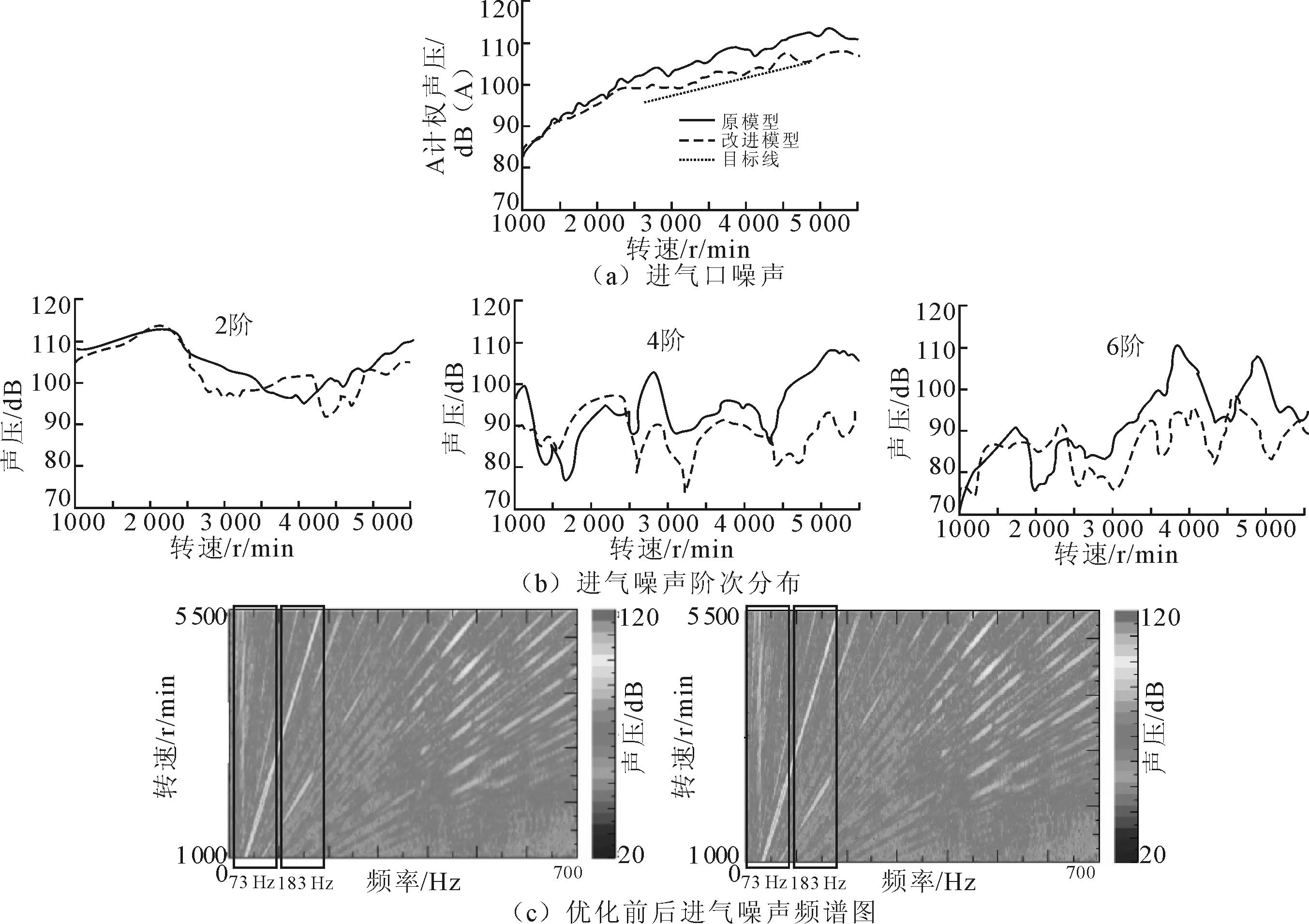
图11　空气滤清器优化后的进气噪声试验结果

从图11(a)中对比改进模型和目标线可知，改进模型进气口噪声基本贴近目标线，但在2 300 r/min、2 750 r/min、3 600 r/min、4 500 r/min转速出现波峰，最大峰值点高出目标线3.2 dB(A)，其它转速段与目标线贴合；与原模型对比可知，在1 500 r/min转速下两者基本重合；1 500～2 500 r/min转速下改进模型在原方案基础上降低1～2 dB(A)左右；在2 500 r/min转速以上(除4 500 r/min转速外)改进模型均降低5 dB(A)左右，其中在4 750 r/min转速降低8 dB(A)。

从图11(b)中可以看出阶次噪声相比于原模型，在低转速一致，在部分中高转速有所降低；4、6阶噪声低转速变化不大，2 500 r/min转速以上改进模型阶次噪声明显整体降低。

从图11(c)可以看出改进模型相比于原模型在73 Hz、183 Hz频段的噪声明显降低；在250～700 Hz频段，改进模型进气噪声幅值有所降低，但整个噪声频带变宽。

4　结论

(1)空气滤清器的声学特性对发动机的进气噪声有重要的影响，空气滤清器的声学特性与进气噪声的良好匹配可以使发动机的进气噪声特性达到优化；

(2)针对原模型进气噪声的问题频率，对空气滤清器做了结构优化，增加了4个谐振腔、一个1/4波长管和一个宽频共振器；

(2)改进模型在某些转速进气噪声贴近目标线，且相比于原模型在2 500 r/min以上转速基本满足要求；

(3)改进模型的进气背压为3.1 kPa，低于原模型3.4 kPa的进气背压，满足目标要求；

(4)改进模型的噪声频带没能完全满足目标要求，由于本次设计未能完全兼顾空气滤清器本身声学特性与消声特性的平衡，需进一步进行改进、计算和验证，为深一步的研究提供参考。

参考文献：

[1]史杰,唐善政,卢曦,等.空气滤清器对车辆进气噪声的影响分析及性能优化[J].汽车技术,2015(4):10-13.

[2]靳晓雄,吴颖江,靳畅,等.空气滤清器的降噪设计与试验[J].机械设计与研究,2009,25(5):100-103.

[3]刘联鋆,郝志勇,刘迟,等.空气滤清器流动阻力与噪声特性的仿真和优化[J].汽车工程,2011,33(12):1092-1097.

[4]金岩,郝志勇,刘永.空气滤清器声学性能的改进设计[J].内燃机工程,2007,28(6):58-60.

[5]庞剑,谌刚,何华,等.汽车噪声与振动:理论与应用[M].北京:清华大学出版社,2005．

[6]贾维新.发动机结构噪声和进气噪声的数字化仿真及优化设计研究[D].杭州:浙江大学,2008．

[7]金岩,郝志勇.针对通过噪声的空气滤清器声学特性研究与改进[J].浙江大学学报(工学版),2006,40(8):1443-1445.

[8]朱廉洁,季振林.汽车发动机空气滤清器消声特性研究[J].汽车工程,2008,30(3):260-263.

[9]贾维新,郝志勇.空气滤清器声学性能预测及低频噪声控制的研究[J].内燃机工程,2006,27(5):67-70.