基于路面平整度的货物约束系统振动响应分析
周 斌,闫鹏磊,赵 燕
(武汉理工大学 机电工程学院,湖北 武汉 430070)
随着交通运输行业及物流的蓬勃发展,货物运输安全问题越来越突出。在我国目前货物运输大多还是使用传统的绳索、网罩等捆绑方式,在运输过程中时常出现散包等事故。因此,推广使用更为安全有效的货物约束拉紧器(以下简称拉紧器)势在必行。拉紧器是货物运输安全的重要组成部分和关键的配套产品,在货车高速行驶中它也能够大大提高货车及货物的安全系数[1-2]。在欧美发达国家拉紧器是作为强制性的标准来使用的,国内目前已经出台了相应的拉紧器标准,但还处于非强制性执行阶段,对于拉紧器在使用过程中对货物的约束效果还处于研究阶段。路面平整度是路面表面相对于理想平面的纵向偏差,是车辆振动系统的主要振源[3-4]。在等级较差的路面上,路面平整度引起的振动有可能会导致货物及包装破损和散包的现象,对货物造成很大危害。同时,由于货运车辆行驶的路况千差万别,基于我国国情,路面等级相对较差的公路所占比率较大,更加容易造成货物运输过程中的损坏。因此研究拉紧器在较差的路面等级下对货物振动响应的影响有重要意义。
通过建立车辆-货物-拉紧器系统的多自由度模型,针对一定路面激励下货物的振动响应问题进行仿真分析。最后讨论拉紧器在不同刚度、不同车速条件下对货物的振动响应的影响。
1 车辆-货物-拉紧器系统动力学模型的建立
拉紧器是一种新型货物捆绑专用器,它由拉紧带、锁紧器和末端装置配套组成。拉紧器实物及其使用如图1和图2所示。选择TD50款拉紧器为研究对象,对车载货物为8 000 kg的货物采用直接捆绑的方式。拉紧器在使用的过程中应预紧,一般标准预紧力STF范围在0.1LC≤STF≤0.5LC之间(LC为拉紧器的捆绑能力,其值等于拉紧器的极限工作载荷)。拉紧器在使用过程中可等效为具有一定弹性和阻尼的粘弹性模型,其模型的等效刚度和等效阻尼计算公式分别为式(1)和式(2)。
(1)
(2)
根据企业提供的拉紧器的有关数据计算得到在工作区间内其平均等效刚度和阻尼K=8×104N/m,C=1.2×103N·s/m[5]。根据研究需要选用东风EQ型载重为8吨的载货汽车,其参数如表1所示。

图1 货物约束拉紧器

图2 拉紧器使用图

名称参数值簧载质量/kg3400前车轮质量/kg325后车轮质量/kg525簧载质心到前车轴的水平距离/m2.2簧载质心到后车轴的水平距离/m4.3簧载质心到货物的水平距离/m1.05前/后轮距/m1.94/1.86前悬架垂直刚度/N/m1.7×105后悬架垂直刚度/N/m4.8×104前悬架垂直阻尼/N·s/m7×103后悬架垂直阻尼/N·s/m1.4×104
车辆-货物-拉紧器系统是一个很复杂的系统,为简化问题的分析做出如下假设:
(1)假设车辆匀速行驶,整车简化为车身质量和非簧载质量;
(2)假设悬架的刚度和阻尼均为常数,用SPRING定义。货物与车身的连接为弹性连接,用BUSHING定义;
(3)拉紧器简化为具有一定刚度和阻尼的约束系统;
(4)路面平整度冲击主要造成货物垂直振动,本研究重点分析货物的垂直振动响应问题。
在运输过程中,货物的振动主要还是来自路面的激励作用,路面激励主要通过车轮、悬架系统,最后通过车身传递到货物上。结合整车13自由度模型[6],简化的系统模型如图3所示。
1.思想认识滑坡。随着农田防护林体系框架的初步建成,生态环境有了明显改善,基本结束了“沙进人退”的历史,人们渐渐淡忘了“风起沙滚”的日子。群众对有无农防林的体会不深,只片面地看到了林带胁地现象,没认识农田林网的屏障作用,对规划的农防林带不能按规划营造,缺株断带的林带不能及时补建,有的地方林农争地矛盾突出,挤占蚕蚀林地现象时有发生,严重制约农田防护林的营造和采伐更新。

图3 车辆-货物-拉紧器简化模型示意图
建立的车辆-货物-拉紧器系统虚拟样机模型如图4所示。模型主要部分有驾驶室、车身、车轮、悬架系统、车轴、货物和拉紧器几大模块。系统共有10个自由度,其中车身和货物均具有沿Z轴平动,绕X轴侧倾运动,绕Y轴俯仰3个自由度,每个车轮有一个沿Z轴平动的自由度。

图4 车辆-货物-拉紧器动力学模型
2 路面平整度下货物的振动响应
2.1 路面平整度时域模型的获取
描述路面平整度特性的指标有很多种,最常用的是根据路面功率谱密度进行数学统计分析。按照国标GB7031-2005《机械振动—道路路面谱测量数据报告》,路面平整度位移功率谱密度拟合表达式采用式(3)[7]。
(3)
式中:n为空间频率;n0为参考空间频率,n0=0.1;w为频率指数,w=2[8];Gq(n0)为路面平整度系数,其大小随路面粗糙度的增加而递增。
对于路面平整度的模拟本文采用谐波叠加法。谐波叠加法的基本思想是将大量随机三角级数进行叠加,在指定频率下达到相应的功率谱密度,从而构造出符合要求的路面模型[9]。根据该方法获得的E级路面谱如图5所示。

图5 E级路面谱
2.2 货物在E级路面下的振动响应
就拉紧器对货物的振动响应问题,以E级路面谱作为输入,研究车辆-货物-拉紧器系统分别在货物有无拉紧器约束时的振动响应问题进行仿真分析。根据国标GB /T4970-2009规定:一般路面试验车速中的N类车辆的车速选择,同时为了研究货物在较快的车速下拉紧器的约束响应问题,选择试验车速为50 km/h,拉紧器刚度和阻尼K=8×104N/m,C=1.2×103N·s/m,仿真时长设置为10 s[10]。图6和图7分别是在E级路面谱车速50 km/h时货物在有无拉紧器约束的情况下的位移、加速度曲线。从图6可以看出在拉紧器约束下货物最大位移为87.6 mm,无拉紧器的约束下货物的最大位移为123.4 mm。从图7可以看出在拉紧器约束下货物的最大加速度为5.9×104mm/s2,无拉紧器约束下货物的最大加速度为1.46×105mm/s2。可以看出在拉紧器的作用下货物的位移以及加速度值都有较大的降低。其加速度均方根从无拉紧器约束的11 584 mm/s2降低到了8 109 mm/s2,货物的振动响应降低了30%左右。图8为货物在有无拉紧器约束情况下的加速度频率响应曲线,由图8可以看出,货物的频率响应峰值发生在1.48 Hz处,表明在此处货物的振动强度最大。另外在10 Hz范围处,加速度也有一定的幅值,表明在此处也存在一定较大强度的振动。因此,在产品设计时,应保证易损部件的固有频率避开低频的范围,避免因发生共振而产生损坏。
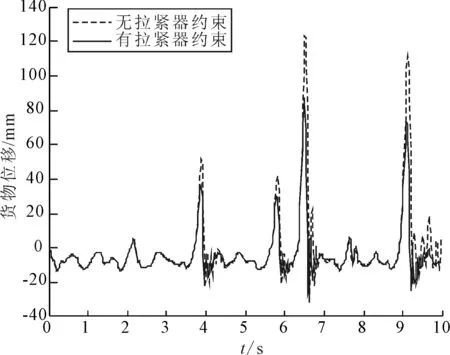
图6 E级路面货物位移曲线
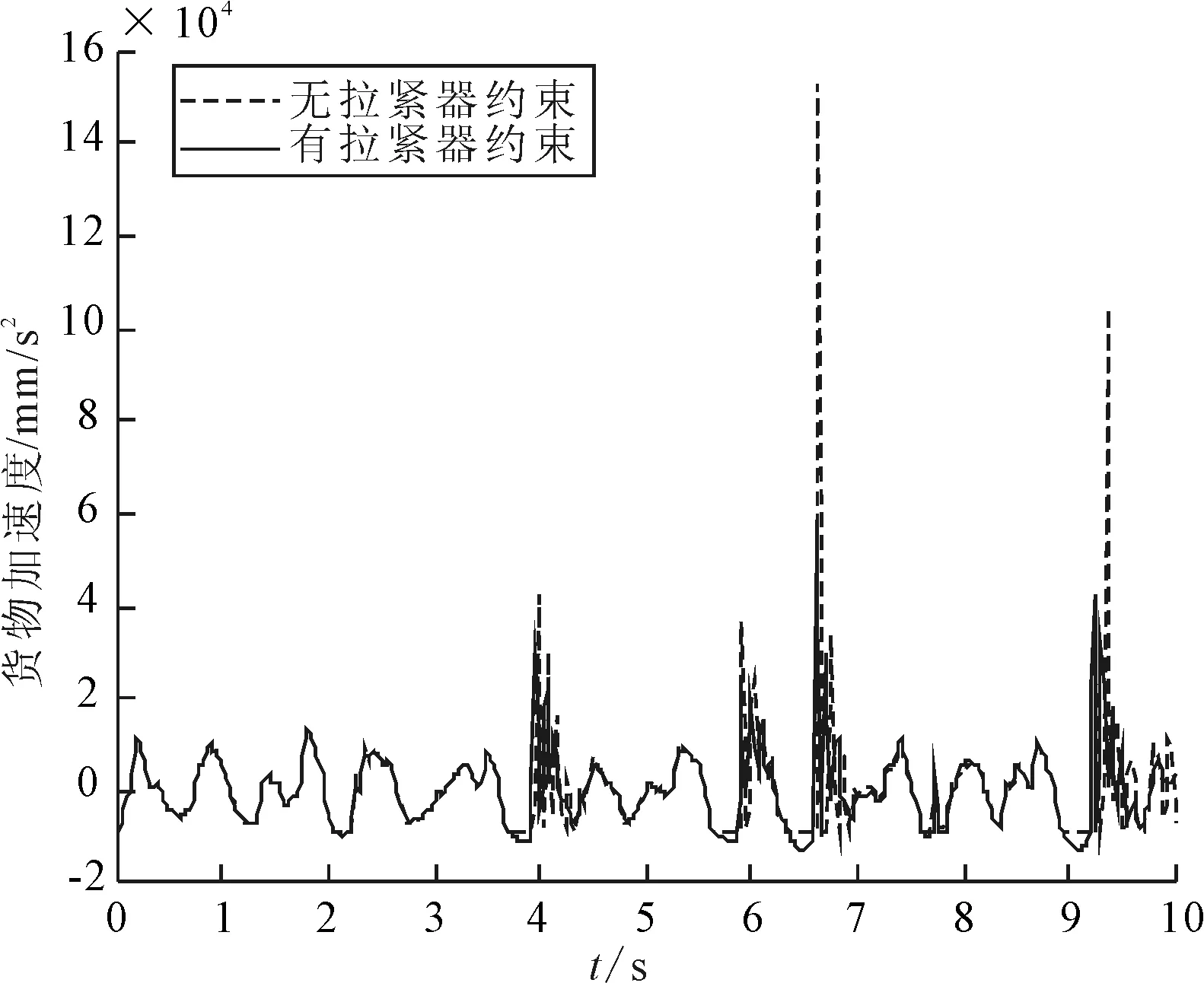
图7 E级路面货物加速度曲线

图8 拉紧器约束时货物加速度频率响应曲线
2.3 拉紧器刚度对货物振动响应特征的影响
为进一步验证拉紧器的使用效果,相同型号的拉紧器配备不同的拉紧带,拉紧带结构、外形尺寸的不同,其等效刚度也不一样。现围绕原始数据K=8×104N/m,C=1.2×103N·s/m,将其刚度以2×104N/m步长变化,阻尼不变(由于阻尼相对刚度对货物振动响应影响较小,在此不再讨论)展开成3组数据。得到拉紧器的刚度对货物位移、加速度以及加速度均方根的影响曲线,分别如图9~图11所示。

图9 拉紧器不同刚度时货物的位移响应曲线

图10 拉紧器不同刚度时货物的加速度响应曲线
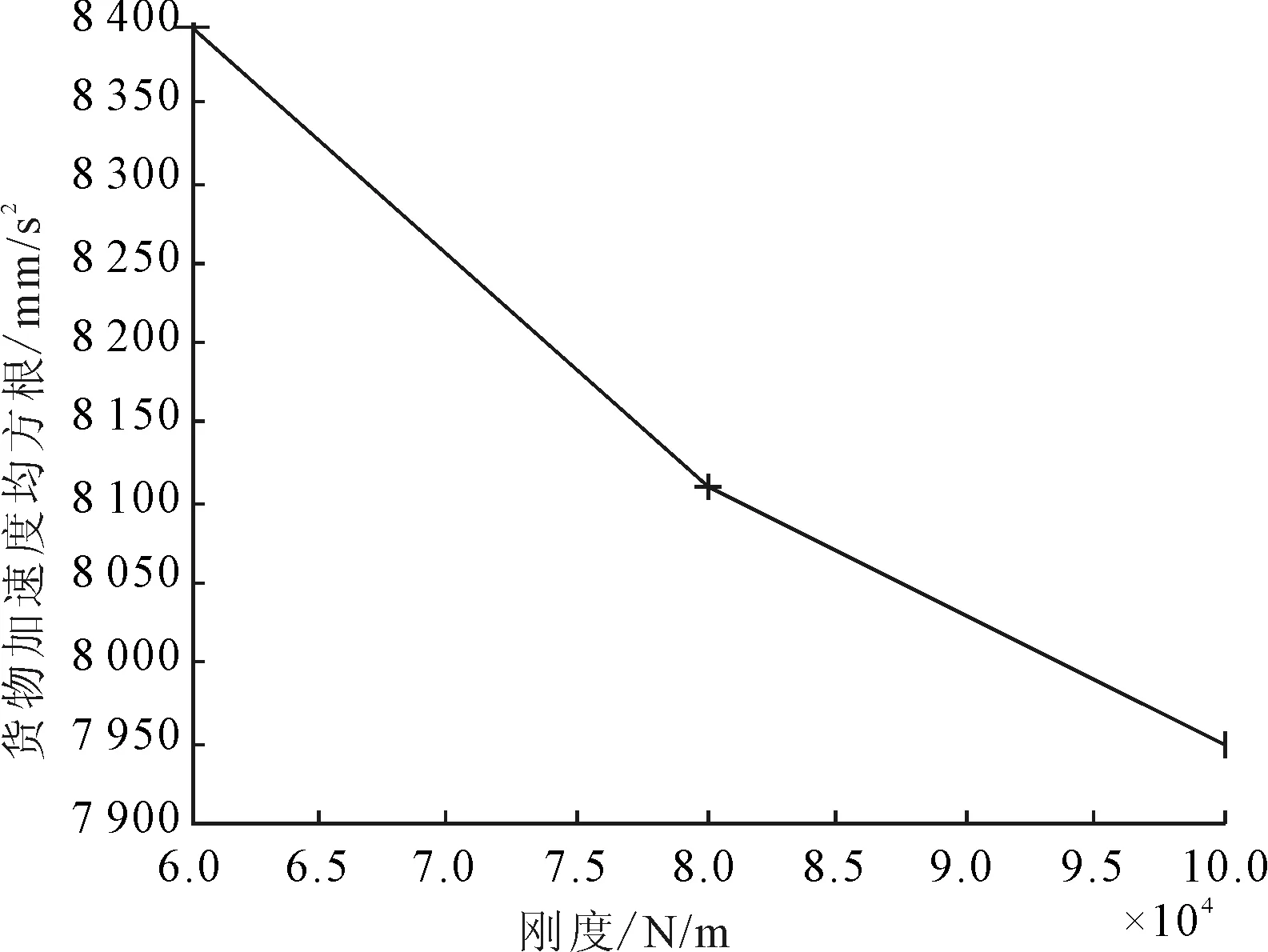
图11 拉紧器不同刚度时货物加速度均方根值的影响曲线
从图9~图11可以看出,随着拉紧器刚度的逐步增加,货物的位移、加速度以及加速度均方根值相应的减小,与实际经验吻合。可为使用者根据不同的货物属性选择适合的拉紧器做出参考。
2.4 车速对货物振动响应特征的影响
车速是影响货物振动响应的重要因素,研究车速对货物的振动响应可以为不同路面等级下选择合理的车速做出理论指导。为此,分别选取40 km/h、50 km/h、60 km/h的车速,拉紧器刚度和阻尼K=8×104N/m,C=1.2×103N·s/m。得到车速对货物位移、加速度、以及加速度均方根值的影响曲线,分别如图12~图14所示,图15为不同车速下货物的加速度频率响应曲线。
从仿真结果可以看出,降低车速可以有效地降低货物的位移、加速度以及加速度均方根。同时,降低车速可以有效地降低货物的振动幅值与范围。这就更加说明司机在行驶的过程中遇到路面较差的情况下一定要减速慢行,保证货物以及人身的安全。

图12 不同车速下货物的位移响应曲线

图13 不同车速下货物的加速度响应曲线
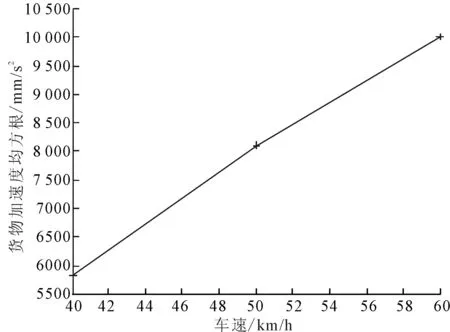
图14 车速对货物加速度均方根影响曲线

图15 车速对货物加速度频率响应影响曲线
3 结论
货物在运输过程中会受到路面平整度的冲击作用产生振动响应,本文建立了货物约束拉紧系统的ADAMS动力学仿真模型,对E级路面平整度激励下的货物约束拉紧系统进行了货物振动响应的分析。同时对于不同拉紧器的刚度以及不同车速下货物的振动响应进行了分析,其结果表明:①货物在运输过程中在低频段其振动程度最为剧烈,在设计产品时应避免其共振频率处在低频区;②提高拉紧器的刚度以及降低车速都可以有效的降低货物的振动响应情况,为货物的安全提供保障;③车速对拉紧器刚度对货物的振动响应的约束有较大的影响,增大车速会减弱拉紧器刚度对货物振动响应的约束。因此,在选择拉紧器时,应根据常用车速选择合适的拉紧器型号,以满足对货物振动响应的约束;④根据上述仿真可知,在较差的E级路面下货物振动的位移和加速度还是较大的,货物的脆值G可能不能承受。因此在运输过程中,可以在货物包装中增加缓冲衬垫或采用缓冲包装,使内部货物与包装之间增加缓冲,从而确保货物安全。在拉紧器和缓冲包装的共同作用下保证货物的运输安全。
参考文献:
[1]胡伟.车辆货物约束系统甩尾力学特性的研究[D].武汉:武汉理工大学, 2010.
[2]汪一立.车辆货物约束系统侧翻力学特性的研究[D].武汉:武汉理工大学, 2010.
[3]Shellock F G, Woods T O. MR Labeling Information for Implants and Devices: Explanation of Terminology[J]. Radiology, 2009,253(1):26-30.
[4]向华荣,张开斌,张琢玉,等.基于伪白噪声的路面不平度模拟及其车辆平顺性[J].重庆工学院学报(自然科学版),2009(9):11-15.
[5]李天鹏,赵燕,李畅达.车辆货物约束系统对道路不平度响应的仿真[J].武汉理工大学学报(信息与管理工程版),2012,34(3):306-309.
[6]王峰,靳永军,张建武.基于整车模型的动力总成悬置振动仿真及优化[J].振动与冲击,2008(4):134-138.
[7]Hu Z G, Zhang Y L, Ye J P, et al. Numerical Modeling and Simulation of Random Road Surface Using IFFT Method[J]. Advanced Materials Research, 2011,199-200:999-1004.
[8]中国汽车技术研究中心.车辆振动输入路面平度表示方法GB/T 7031-86[S].[S.l.]:[s.n.],1986.
[9]夏均忠,马宗坡,白云川,等.路面不平度激励模型研究现状[J].噪声与振动控制,2012(5):1-5.
[10]宁士翔,苏小平,王宏楠.基于ADAMS/Car对车架动载荷的仿真分析[J].机械科学与技术,2014,33(2):289-292.

