离心摆式从动盘减振器减振仿真分析
何佩芸,苏楚奇,王 东,武俊杰
(1.武汉理工大学 汽车工程学院,湖北 武汉 430070;2.武汉理工大学 现代汽车零部件技术湖北省重点实验室;湖北 武汉 430070;3.中国汽车技术研究中心 汽车工程研究院,天津 300300)
前置后驱汽车传动系统的扭振问题一直较为突出,是引起车内振动、噪声的主要激励源之一[1]。目前汽车上主要使用安装在离合器从动盘中的螺旋弹簧式扭转减振器衰减传动系统的扭振。受离合器空间结构的限制,其减振弹簧安装半径较小,弹簧转角范围有限,导致减振效果有限[2]。
离心摆式减振器(centrifugal pendulum vibration absorber, CPVA)在航空领域得到了广泛应用。由于摆的安装空间局限性及汽车发动机运行工况的复杂性,限制了离心摆式减振器在汽车领域的应用[3]。目前LuK公司已开发专利产品,成功将其运用至双质量飞轮及离合器从动盘中[4-5],近年来有不少学者研究了CPVA在双质量飞轮上的应用[6-7],但学者们对CPVA在从动盘上运用的研究较少。笔者系统地介绍CPVA的结构、基本原理及固有频率的推导,基于某前置后驱汽车传动系统存在的扭振问题,应用AMESim软件建立了动力传动系统扭振模型及CPVA仿真模型,并利用扭振试验验证模型的正确性,进而利用计算机仿真分析CPVA在汽车传动系扭振控制中的应用效果。
1 离心摆式减振器的理论分析
1.1 离心摆式减振器结构
CPVA由圆柱形的滚柱、带有弧形滑道的离心摆及法兰组成,其连接形式如图1所示,目前汽车上CPVA主要内置于双质量飞轮或离合器从动盘中,其中离心摆式从动盘减振器结构如图2所示,二者都是连接发动机与变速箱的传动系部件,其所处的空间非常有限。限制CPVA在汽车上应用的难题在于,如何在有限的空间内尽可能多地布置离心摆质量块,同时合理安排滚柱的滑道,使得离心摆可以获得最大的摆块摆角,从而更加充分地利用有限的离心摆质量,最大程度提升减振效果,提升用户的乘坐舒适性。

图1 离心摆的连接形式

图2 离心摆式从动盘减振器结构图
1.2 CPVA的减振机理
当与离心摆法兰铆接离合器从动盘出现转速波动时,在波动的冲击力下,离心摆块与法兰之间将呈现一定的角度差,此时滚柱会在离心摆块的拖动下在滑道内做往复摩擦运动,直至离心摆与法兰转速相同,消除转速差,系统恢复稳定状态,从而实现减振作用。CPVA由于其离心力的作用,离心摆的振动频率可随发动机转速的变化而变化,因此其可用于发动机转速范围内主阶振动的减振。
针对离心摆运动的圆形路径,分析CPVA的基本性能。离心摆运动简图如图3所示,其中G0为转子的质心,GCPVA为离心摆的质心,R为转子的质心到附着点A的距离,r为离心摆的质心到附着点A的距离,离心摆的摆锤质量为m,摆锤通过附着点A连接在转子上,并标明了附接点A和摆锤质量加速度的分量。
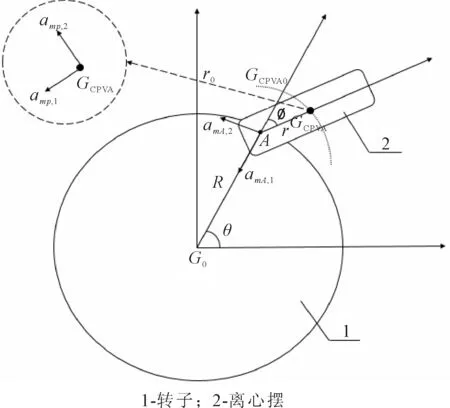
图3 离心摆运动简图
摆锤的加速度是点A处的加速度和摆锤相对于点A加速度的矢量和。由事实可知,点A的瞬时速度为0,故可推导出如下表达式:
(1)
其中:θ为转子所转过的角度;φ为离心摆相对于摆在转子上的连接点所转过的角度。假设摆锤摆动角度十分微小,此时cos(φ)≈1,sin(φ)≈φ,而转子以一个稳定的转速Ω转动,而稳定的转动中带有一个微小的以幅值为μ0,频率为ω的正弦规律变化的波动,于是摆锤有如下的方程:
(2)
在该假设下,现分析CPVA的动力学特性,摆的固有频率可推导为如下形式:
(3)
这是CPVA最重要的特性,摆的固有频率与转子的转速成比例地变化,该特性对于CPVA在汽车上的应用非常有用。施加扭矩的频率与发动机的转速成比例,故CPVA可以看作为是由弹簧悬挂的摆锤,以转速改变其刚度,从而实现在不同转速下的持续减振效果。
2 扭振仿真模型的建立及验证
2.1 扭振仿真模型的建立
本文的研究对象为某自主品牌前置后驱汽车,搭载1.6 L直列4缸汽油机、5速手动变速器。该车传动系统原始配置为单质量飞轮及传统的离合器从动盘螺旋弹簧式扭转减振器。
以4档(直接档)为研究档位,根据传动系统扭振建模原则[8],将动力传动系统简化为18自由度当量系统模型,动力学参数见表1。使用AMESim软件分别建立自由振动模型和强迫振动模型[9],如图4所示。

图4 传动系统当量模型
2.2 扭振仿真结果分析
通过对上述模型的自由振动仿真分析,得到系统的1~5阶固有频率分别为1.13 Hz、4.84 Hz、16.13 Hz、19.09 Hz、57.25 Hz。
通过对上述模型的强迫振动仿真分析,4缸4冲程发动机对于扭振的主激励为2阶,故本文只考虑2阶激励下的强迫振动响应。扭转振动不同于一般的弯曲振动可用振动位移描述,直接测量旋转体的轴线振动很困难,这里以旋转体的转速波动来描述该旋转体的扭振幅值。图5为4档时变速器输入轴和主减速器输入轴的扭振幅值随发动机转速变化的曲线,由图5可知,两测点在1 500~2 000 r/min范围内的转速波动幅值存在峰值,阶次频率计算公式如下:
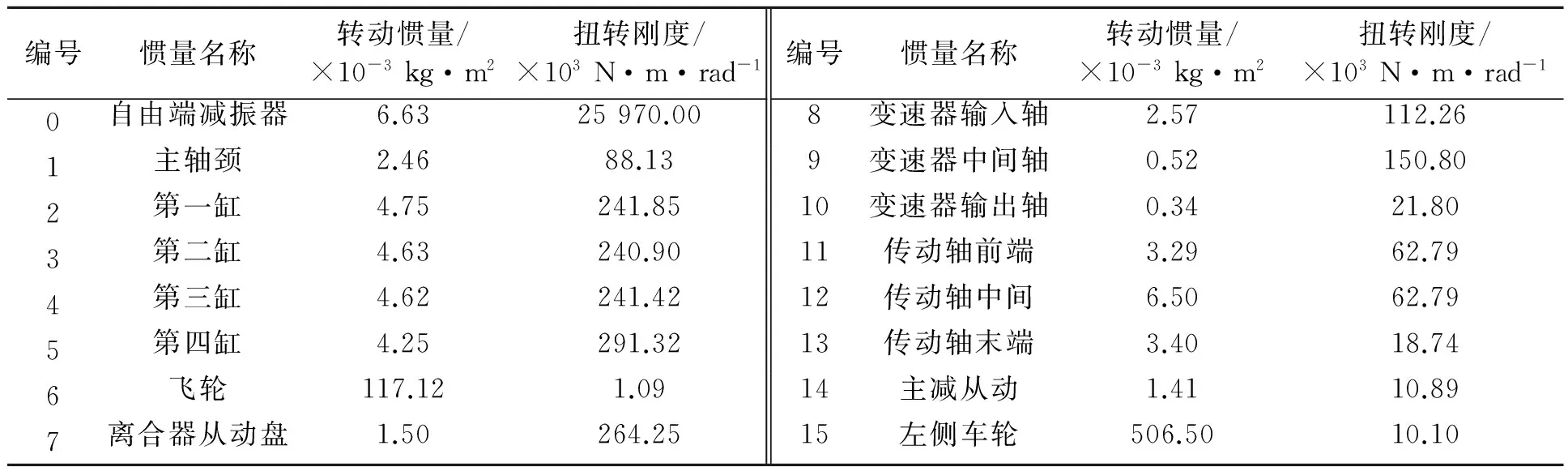
表1 传动系统动力学参数
(4)
式中:n为发动机转速;v为发动机主阶次,可求得峰值对应的频率约为50~66.7 Hz。结合自由振动的分析结果可知,该共振是由发动机2阶激励引起的动力传动系统第5阶模态的共振,对应频率为57.25 Hz。
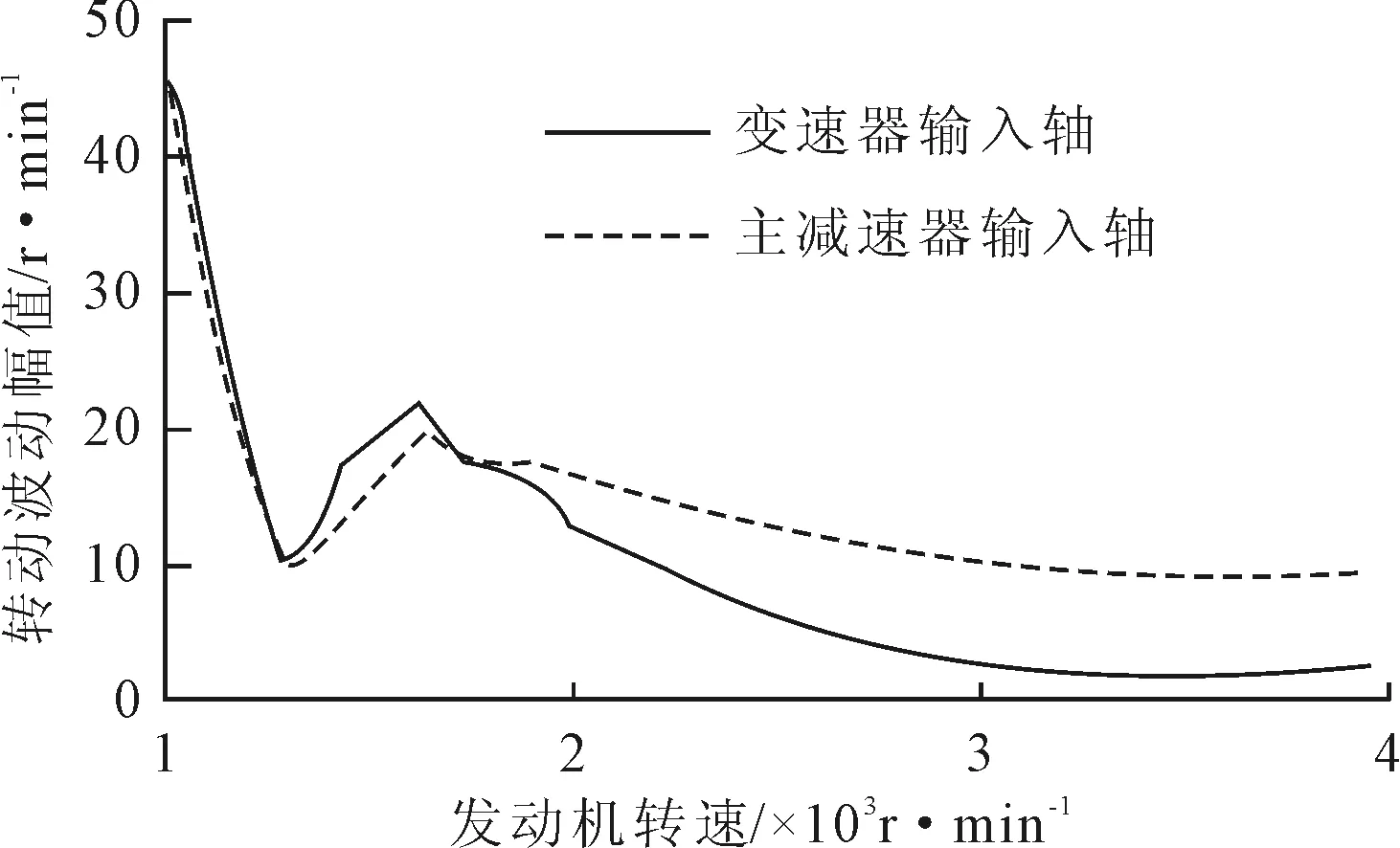
图5 4档强迫振动响应分析曲线图
2.3 扭振试验及模型的验证
为了验证扭振仿真模型的正确性,在整车半消声实验室的底盘测功机台上进行了动力传动系统扭振试验。测点选定为变速器输入轴及主减速器输入轴,两个测点传感器的安装位置如图6所示,扭振试验系统的构成如图7所示。

图6 扭振试验测点

图7 扭振试验系统
试验采用全油门(WOT)加速工况,按照实际情况,对3~5档分别进行1 000~5 000 r/min、1 000~4 000 r/min、1 000-3 000 r/min转速范围的试验,根据测取转速的峰值变化来推算扭振模态频率,并对每个档位的工况进行3次试验,试验数据处理取3次试验的平均值。试验结果表明,各档位2阶转速波动峰值出现的转速分别为3档1 960 r/min、4档1 630 r/min、5档1 575 r/min,据此推测出扭振模态频率分别为65.33 Hz、54.33 Hz、52.50 Hz。自由振动计算结果与试验所得传动系统模态频率对比见表2。仿真计算可以得到多阶模态信息,但试验仅能依据共振峰值推测模态频率,因此只能将频率相近的结果进行对比分析。提取4档(直接档)工况测点的2阶转速波动幅值,与仿真数据进行对比,结果如图8所示。

表2 单质量飞轮系统仿真与试验模态频率对比
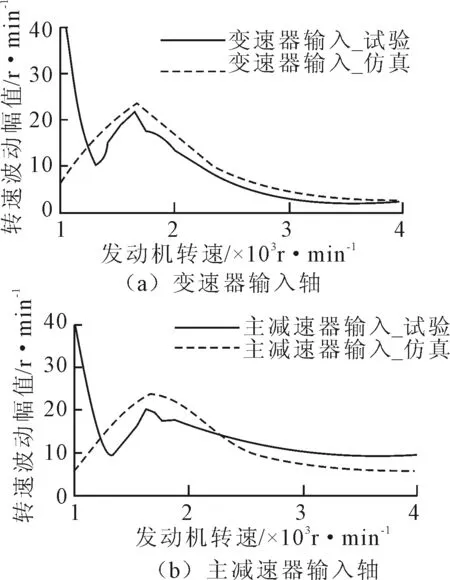
图8 仿真与试验结果对比
从表2和图8分析可知,传动系统扭振模态频率的计算与试验值误差小于5%,强迫振动响应的计算值与试验值在低转速段有差别,初步推测是滚振引起的共振峰值所致;中高转速段变化趋势基本一致,扭转振动重点关注的共振峰重合度较好,由此说明模型参数模拟扭转振动是准确的,所建的扭振模型是可行的,可以用于CPVA的仿真分析。
3 离心摆式减振器的减振仿真分析
利用AMESim搭建离心摆式从动盘减振器的整车动力传动系统4档的仿真模型,以分析CPVA在汽车上的减振效果。
3.1 离心摆式从动盘减振器仿真模型的建立
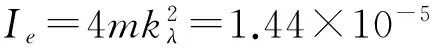

图9 带CPVA的离合器从动盘仿真模型

图10 CPVA计算初始位置简图
3.2 离心摆式从动盘减振器仿真结果分析
根据仿真模型的搭建,取变速器输入轴(即离合器输出轴)转速波动幅值为分析目标,所研究车型的普通离合器从动盘系统的转速波动幅值与离心摆式从动盘减振器的转速波动幅值对比曲线如图11所示。

图11 离心摆式从动盘减振器效果验证对比图
从图11中可看出,离心摆式从动盘减振器明显降低了在常用转速范围内的转速波动峰值,减振效果良好。
4 结论
本文应用AMESim软件建立了前置后驱汽车普通离合器从动盘的扭振仿真分析模型,并进行了试验验证,证明所建立的仿真模型是可行的。利用AMESim搭建了离心摆式从动盘减振器的整车动力传动系统4档的仿真模型,仿真分析研究表明,离心摆式从动盘减振器能有效降低车辆加速过程中的最高转速波动幅值,说明离心摆式从动盘减振器在汽车传动系的扭振控制中具有良好的应用前景。
参考文献:
[1]王东亮,张敬义,闫兵,等.柴油发电机组联轴系统设计研究[J].铁道机车与动车,2014(11):1-5.
[2]王震,邢立明.离合器从动盘扭转减振器损伤分析[J].汽车运用,2013(5):44-44.
[3]李伟,龙岩,史文库.离心摆式DMF—CS扭振减振器隔振性能分析[J].中国机械工程,2009,20(15):1787-1790.
[4]张延辉.LuK最新研发出带离心摆的双质量飞轮[J].轻型汽车技术,2008(Z3):50-50.
[5]俞庆华.舍弗勒新型离合器从动盘进一步丰富了传动系减振方案[J].汽车零部件,2017(2):12-17 .
[6]Wedin A. Reduction of Vibrations in Engines Using Centrifugal Pendulum Vibration Absorbers[D]. Goteborg :Chalmers University of Technology, 2011.
[7]Li W, Gao T, Cui Y, et al. Study and Simulation of Isolation Performance of Torsional Vibration of DMF-CS with Centrfugal Pendulu-Type Absorber[C]∥ Proceedings of the FISITA 2012 World Automotive Congress. Berlin:Springer, 2013:121-133.
[8]王东,闫兵,王东亮,等.汽车传动系扭振引起的车内轰鸣声控制方法[J].噪声与振动控制,2015,35(2):73-76.
[9]周林,郑四发,连小珉.加速工况下传动系统扭转振动分析[J].振动工程学报,2010,23(6):601-605.

