基于SVM的多足机器人故障诊断系统
王 委 蒋 刚 留沧海
(1.西南科技大学制造科学与工程学院 四川绵阳 621000;2.西南科技大学制造过程测试技术教育部重点实验室 四川绵阳 621000)
多足机器人在非结构路面环境下能够更加灵活地行走跑跳[1],广泛应用于军事运输、外星探测、地震救援等诸多领域[2-4]。在军事领域,机器人损伤可能导致其无法执行运输、救援、探测等任务,贻误战机。在外星探测领域,一颗螺钉的松动可能导致巨大的经济损失。在地震救援领域,机器人无法正常工作可能导致本可得救的人失去生命。在日常工作中,人们可以发现大部分的损伤并及时采取措施,但多足机器人由于其非结构路面上的可通过性优势,往往被紧急调派到恶劣环境中工作,因此设计一套专门针对恶劣环境下多足机器人自身的健康监测系统非常重要。
目前有很多学者研究机械结构损伤检测。郑渝等[5]以大型直线振动筛的下横梁为研究对象,采用声发射技术与动力学健康监测相结合的方式确定结构损伤的部位与损伤的程度。肖君柽等[6]采用有限元等方法对H型钢和钢管结构的导波传播机理进行了研究,并进行了损伤定位实验。
也有很多学者将支持向量机用于损伤检测方面。彭冰洁等[7]通过识别特定频段的信号成分,提出了基于多尺度熵(MSE)和支持向量机(SVM)的损伤定位方法,实现了对薄板结构不同故障类型的区分。邹龙庆等[8]利用支持向量机优良的回归特性,并将柔度矩阵作为结构损伤检测目标,提出了一套结合了支持向量机和柔度矩阵的针对石油井架的结构损伤识别技术。杨景超等[9]采用支持向量机进行模式识别,并根据希尔伯特黄变换(HHT)理论比较选取敏感的损伤指标,验证了该方法在震后桥梁结构损伤识别中的可行性和实用性。上述方法均是将支持向量机方法应用于薄板、井架、桥梁等规则的固定件上,而机器人结构是不规则的运动件。
本文针对大型重载六足机器人腿部结构展开研究,针对不同类型的损伤结构记录其振动数据,利用傅里叶变换提取不同状态的特征量,构建SVM训练模型,并用交叉验证的方法检测该模型的识别准确率,最后将实验结果与使用RBF神经网络的方法进行对比,证明SVM方法进行模式识别的优越性。
1 SVM理论
传统统计理论往往需要大量的样本数据才能得到满意的识别效果,统计学习理论是一种专门针对小样本的机器学习理论,在其基础上发展起来的SVM(支持向量机)方法能够非常好地处理模式识别问题。
设有n个线性可分样本,记作{(xi,yi)},i=1,2,…,n,n为训练样本个数。其中,特征向量xi∈Rd,d为特征向量维数,类别标签y∈{-1,+1}。最优超平面是使分类间隔最大的分类平面。即满足
s.t.yi[(wTxi+b)]≥1,i=1,2,…,n
(1)
式中,w为分类面的权系数向量;b为分类域值。最终可将问题转化为对偶问题:
(2)
对于非线性软间隔可分样本,需要解决区分非线性可分样本和弹性划分类别两个问题。
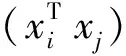
对于非严格可分的样本,可以通过增加松弛变量来求解软间隔分类超平面。对线性不可分问题,引入惩罚因子C和松弛变量ξi≥0。
于是,式(1)变为:
s.t.yi[(wTxi+b)]≥1-ξi,
ξi≥0,i=1,2,…,n
(3)
式中,w为分类面的权系数向量;b为分类域值。
式(2)变为:
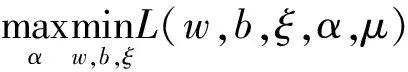
αi{yi[(wTφ(xi)+b)]-1+ξi}=0,i=1,…,n
(4)
式中,αi,μi为优化系数。αi≠0的样本为支持向量(SVs),它们是距离分类超平面最近的样本,决定了最终的分类结果。分类决策函数为
(5)
使用不同的内积核函数会产生不同的结果,常用的核函数有线性核函数、多项式核函数、RBF核函数和多层感知器核函数。
2 SVM故障诊断方法
2.1 多类故障分类器
SVM实际上是一个二分类器,即决策函数只有+1和-1两个值。实际中,常会遇到多类分类,目前采用的方法主要有两种:
(1)一对多法(1-v-r SVMs)。训练时需要针对m个类别构建m个SVM分类器,该SVM分类器负责将第k类的样本和其余类别的样本区分开。
(2)一对一法(1-v-1 SVMs)。训练时需要针对m个类别构建m(m-1)/2个SVM分类器,该SVM分类器负责将其中两类样本区分开。之后对每个类别进行投票,得票最多的类别即为该未知样本的类别。
本文采用一对一法进行多类分类。将样本分为a,b,c,d四类。将测试样本x分别输入给分类器1至分类器6,如图1所示,得票数最多的类别即为x所属的类别。
本文实验中,经分类效果对比选用2阶线性核函数,选取惩罚系数C=1。
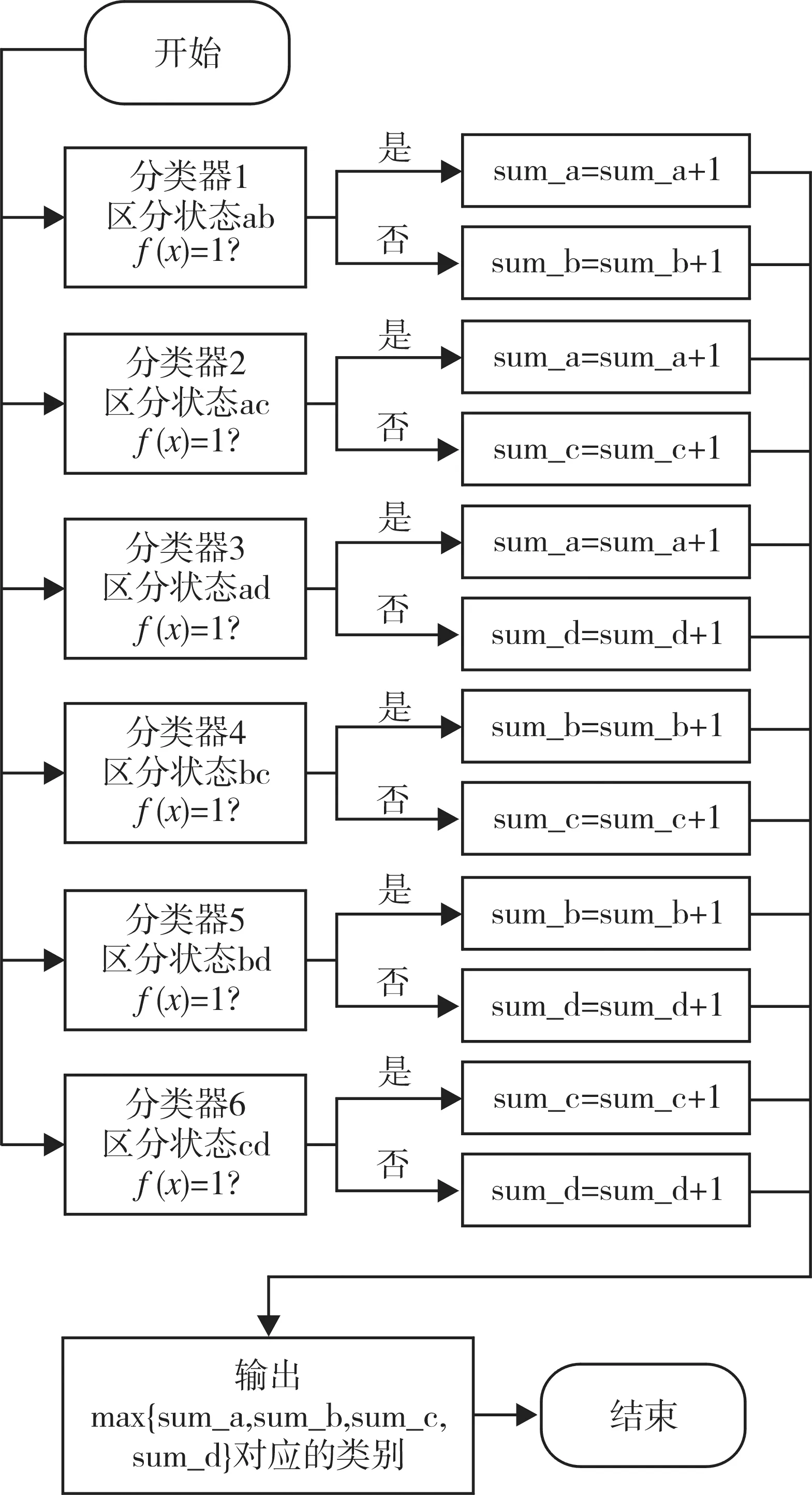
图1 四分类流程Fig. 1 Four Classification Process
2.2 故障分类实验
本实验在卢晴勤[10]及团队共同完成的大型重载液压驱动六足机器人Pro/E模型的基础上展开,该六足机器人长5.5 m,宽5.5 m,高2.0 m,如图2所示。

图2 六足机器人模型Fig. 2 Six-foot Robot Model
首先,分析易损伤结构,针对a,b,c,d即正常、膝关节轴套松动、小腿损伤以及膝关节轴套松动且小腿损伤4种状态进行三维建模。之后,对每个模型进行21次ADAMS仿真实验,共得到84组时域振动数据。基于SVM的多足机器人运动部件故障诊断单次试验流程如图3所示。
为了模拟真实情况,同种状态下的每个样本以相同的过程实现,但初始位置略有不同。例如,样本1的实现方式为初始位置时大腿油缸两耳朵之间距离为728 mm,小腿油缸两耳朵之间的距离为675 mm,令此时足端与地面距离为20 mm,之后控制大腿油缸匀速伸长,直至与地面发生碰撞。样本2与样本1实现方式的不同在于令小腿油缸两耳朵之间的距离为675.5 mm。此后每个样本都以这样的方式实验。在实际的测试实验中,对于长度为2 m的构件来说,前后1 cm的误差是可以存在的。由此完成不同样本的测试实验。
将84个样本的时域振动信号作为初始数据读入MATLAB,提取所有样本的频率和振幅作为分类特征。
4种情况下典型样本的时域及频域图像如图4、图5所示。
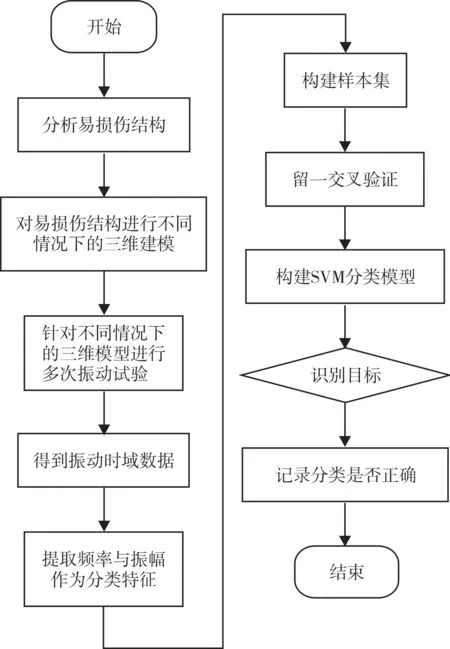
图3 基于SVM的试验流程Fig. 3 Test flow which based on SVM
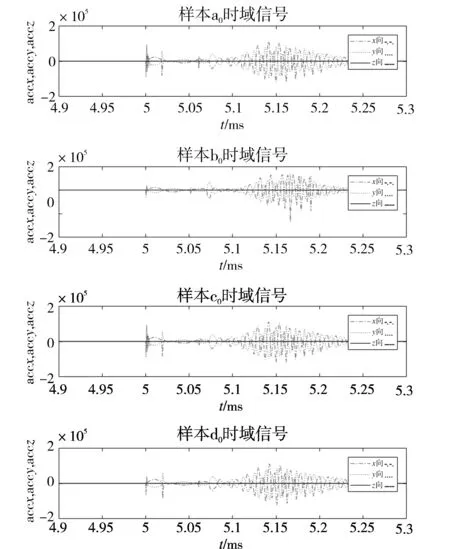
图4 4种情况下典型样本的时域图像Fig.4 Time-domain images of typical samples in four cases
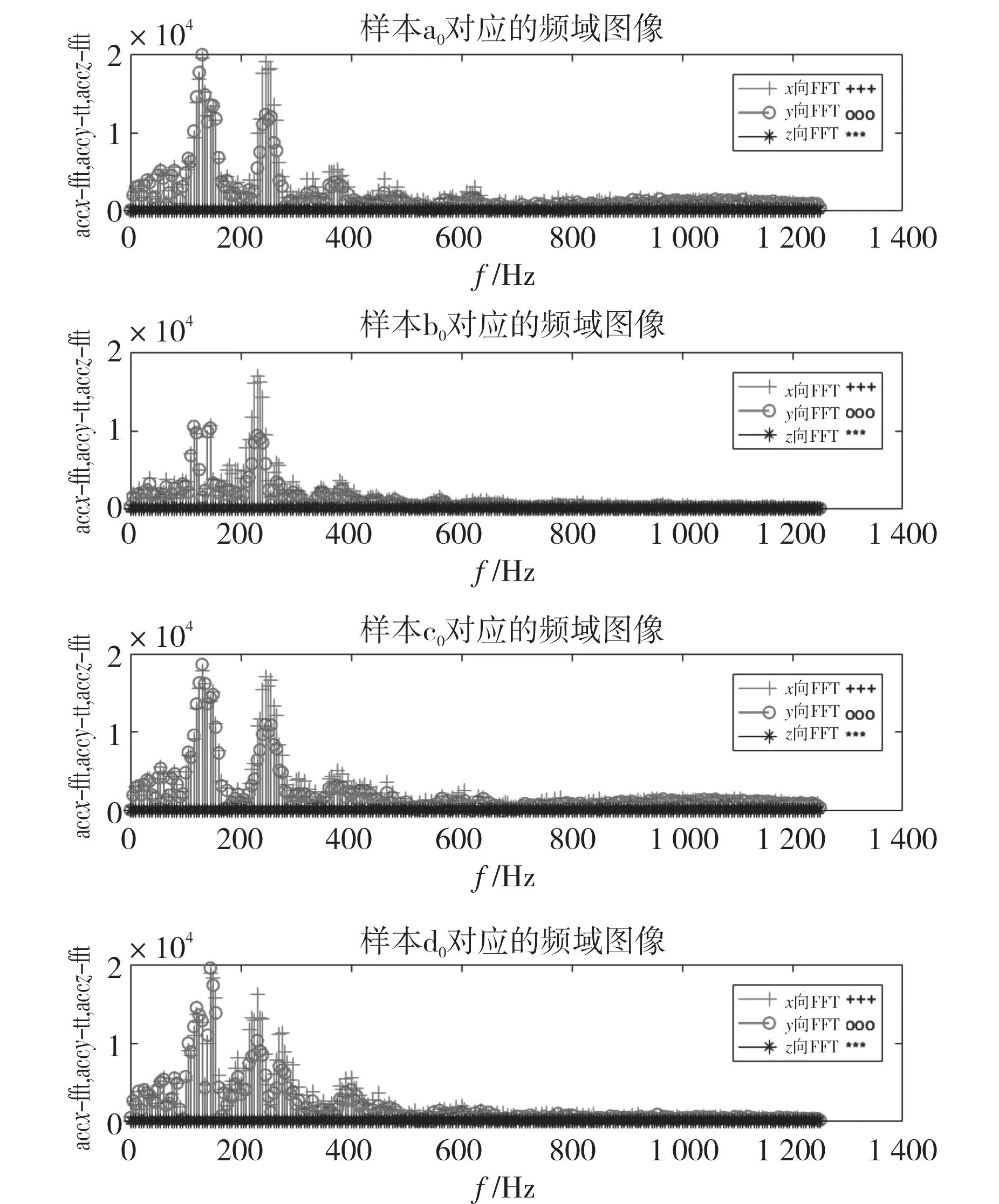
图5 4种情况下典型样本的频域图像Fig.5 Frequency-domain images of typical samples in four cases
由图4可以看出,由于足端与小腿之间为自适应球铰连接,在足端与地面接触的初始时刻,足端与地面之间为点接触状态,形成较大的冲击,经过一段时间的调整,才形成比较规律的模态振动数据。对规律的模态振动数据进行傅里叶变换得到频域数据,提取频率与幅值作为识别特征。对4种损伤状态的所有样本添加样本标签,类别标签分别为0,1,2,3。对所有样本进行留一交叉验证,即每次取其中一个样本作为测试样本,并用其余83个样本构建SVM分类模型和RBF神经网络模型(对照组),循环83次,记录识别准确率等指标。结果如表1所示。
3 实验结果分析
对所有样本进行交叉验证,用SVM分类的正确率为90.47%,测试时间为0.009 2 s,而RBF神经网络对应的分类正确率为77.38%,测试时间为1.642 0 s。这说明在小样本情况的同等条件下,SVM比RBF神经网络具有更好的分类性能和更强的推广能力。
SVM的训练时间只有RBF神经网络训练时间的一半,测试时间更是后者的0.5%。这表明,两种方法的时间消耗主要用在构建训练模型上,测试未知样本类别所占时间很少,在0.7%~4%,因此一旦训练模型构建完成,两者都可以对机械结构损伤状态进行在线模式识别,但SVM比RBF神经网络的性能更优。分类结果如表1所示。
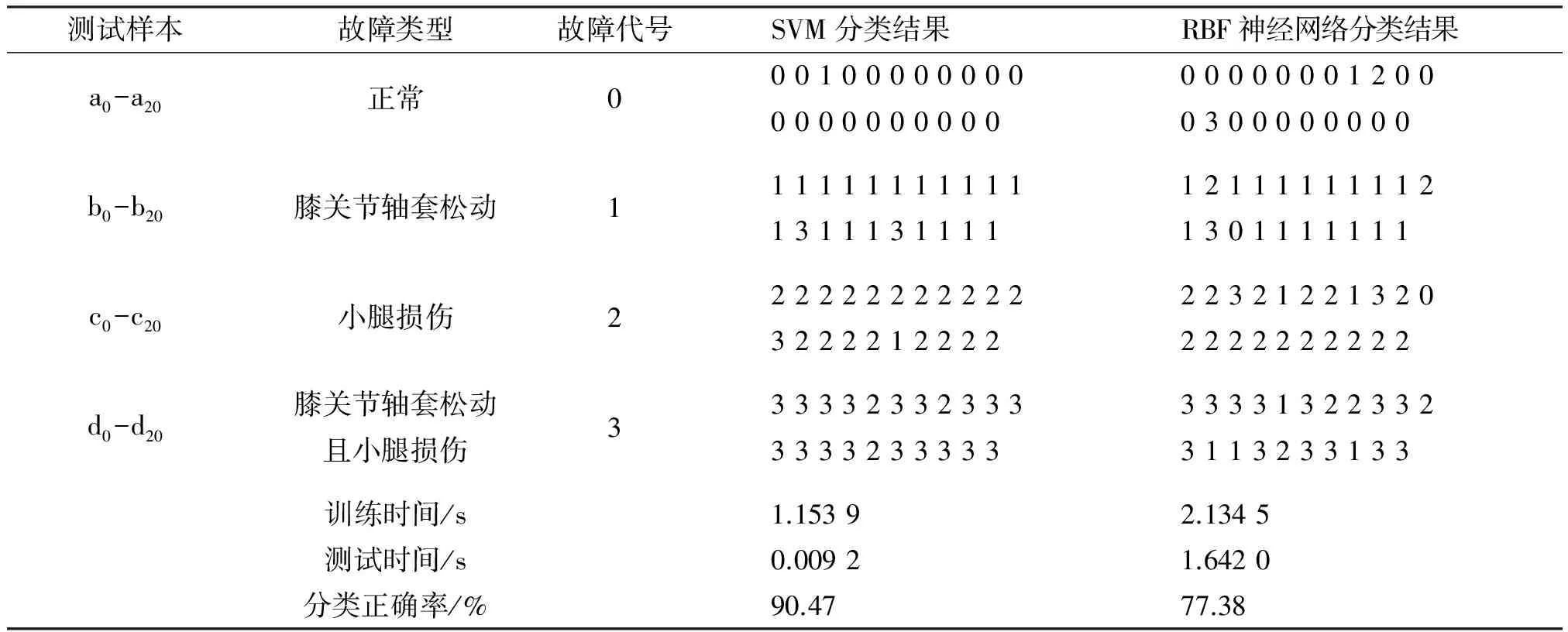
表1 SVM多类分类结果与RBF径向基神经网络分类结果对比Table 1 Comparison of SVM classification results and RBF neural network classification results
4 结语
(1)通过在机器人工作过程中记录其腿部振动数据,提取机器人运动过程中的模态频率和振型作为特征量,利用SVM算法构建识别模型是一种很好的损伤判别方法。在针对大型重载六足机器人腿部的4种故障(含正常情况)模式识别中,表现出优异的分类性能。
(2)在小样本条件下,SVM方法比RBF神经网络在更短的时间内具有更高的分类准确率。
[1]卢晴勤, 留沧海, 刘佳生, 等. 液压驱动六足跳跃机器人仿真分析[J]. 机械设计与制造, 2015, (8):200-205.
[2]ZHANG H, LIU Y, ZHAO J, et al. Development of a bionic hexapod robot for walking on unstructured terrain[J]. Journal of Bionic Engineering, 2014, 11(2):176-187.
[3]WANG Y, ZHU H, WANG Y S, et al. Current Status and Technical Problems in Research of Coal Mine Rescue Robot[J]. Coal Mine Machinery, 2007, 22(6):5-8.
[4]SHIGEO H, KEISUKE K. Study on quadruped walking robot in Tokyo Institute of Technology-past, present and future[C]// IEEE International Conference on Robotics and Automation, 2000. Proceedings. ICRA. IEEE, 2000, 1:414-419.
[5]郑渝. 机械结构损伤检测方法研究[D]. 山西太原:太原理工大学, 2004.
[6]肖君柽. 基于超声导波的机械结构健康监测机理研究[D]. 陕西西安:长安大学, 2015.
[7]彭冰洁. 机械结构损伤分析与故障识别方法研究[D]. 湖北武汉:武汉理工大学, 2014.
[8]邹龙庆, 陈桂娟, 付海龙,等. 基于柔度矩阵和支持向量机的井架损伤识别技术[J]. 石油矿场机械, 2008, 37(2):1-4.
[9]杨景超. 基于HHT和SVM的震后桥梁结构损伤诊断研究[D]. 四川成都:西南交通大学, 2014.
[10] 卢晴勤. 大型重载液压驱动六足机器人的步态控制研究[D]. 四川绵阳:西南科技大学, 2016.

