双弧面凸轮式ATC机械手的刚柔耦合动力学分析

葛正浩， 李佳蔚， 梁　辰

(陕西科技大学 机电工程学院， 陕西 西安　710021)

0　引言

自动换刀机械手用于数控机床加工中心，具有换刀时间短、重复定位精度高等优点.自动换刀机械手可实现连续换刀以减少非切削时间，避免多次装夹工件造成误差，进而提高生产率、降低生产成本.为适应加工中心的多功能化需求，20世纪60年代发达国家便开始研究自动换刀机械手，80年代初国际标准化组织制定发表了数控刀具锥柄的国际标准，从而形成了自动换刀系统统一的结构模式[1,2].

奥地利ANGER公司研制生产的HC、HCH加工中心是切削对切削换刀速度最快的加工中心，其换刀方式为多主轴换刀，即将夹具工件来回穿梭于各主轴之间以完成换刀，使切削对切削的换刀时间降为0.4 s；德国Burkardt和Weber GmbH公司研制了带有转塔刀库的STAMA MC2014、MC325-TW等加工中心，由于转塔式刀库可换位，换刀时间即为换位时间与进给时间之和，其切削对切削换刀时间为2 s[3]；日本MAZAK公司开发出带有回转式自动换刀机械手的FH480卧式加工中心，其刀对刀换刀时间只需1.3 s，切削对切削换刀时间为4.0 s.

我国学者以提高自动换刀机构的定位精度和运转平稳性为目的，也开展了广泛的研究.比如北京邮电大学的董海洋[4]研究自动换刀机械手的换刀性能，搭建了凸轮式自动换刀机械手虚拟平台以分析换刀过程中机械手的受力薄弱点，并运用ANSYS和ADAMS对新型换刀机械手进行了优化分析；北京机械工业学院的王科社等[5]基于自动换刀机械手换刀时间的计量方法，研究了国内外快速自动换刀机械手中具体的刀对刀换刀时间、切削对切削换刀时间等换刀特性；集美大学的张文光等[6]借助Matlab及Solid Works软件编程和计算各项设计参数来完成换刀机构的实体建模，并利用Master CAM软件设计了换刀机械手中多头弧面分度凸轮数控加工仿真的新方法.

目前，虽然对换刀机构的动力学研究较为充分，但是对凸轮式换刀机构尤其是对双弧面凸轮型的换刀机构动力学研究还较浅，并且普遍的研究方法为多刚体仿真分析.因此本文的创新点在于通过建立换刀机构的刚柔耦合虚拟样机来分析机构的动态性能.

本文基于刚柔耦合的动力学理论研究了双弧面凸轮式自动换刀机械手柔性构件选取的问题并建立了整机的刚柔耦合虚拟样机，使动力学模型更加契合实际情况，并在此基础上进行了整机的动态性能研究，验证了模型的正确性和机构的实用性.

1　双弧面凸轮式ATC机械手的原理

双弧面凸轮式ATC机械手的回转运动通过多头弧面凸轮机构来实现，摆动滚子从动件弧面凸轮机构驱动拨叉控制手臂的往复直线运动，具体的换刀过程如图1所示.这种ATC装置的特点在于弧面凸轮机构将主轴的旋转运动转换成了输出轴的往复直线运动，克服了传统摆动机构传动间隙大、振动冲击大的缺点.其结构如图2所示.

图2　双弧面凸轮式ATC机械手结构图

2　双弧面凸轮式ATC机械手刚柔耦合建模

由于在实际的生产运行过程中，有些零件会产生弹性变形，如果还用多刚体模型进行分析的话，则不能正确表现机械系统的实际运行状态.于是在仿真过程中将机构在工作时容易产生弹性变形或者变形量较小但对机械系统的运行工作精度影响较大的构件定义为柔性体，而将其他在工作时不易产生弹性变形或者变形情况对系统精度影响较小的构件定义为刚性体，建立换刀机构刚柔耦合虚拟样机，使整个机构的运行状态和实际情况更加契合.

2.1　刚柔耦合动力学模型的建立

从机械的角度来说，动力学系统一般受到四个主要因素：系统的惯性、弹性、激励和阻尼的影响[7].建立双弧面凸轮机构ATC机械手的动力学模型时，要将实际工作状况和动力学的影响因素综合起来考虑，建立出在可以对动力学方程进行求解的前提下，尽量契合实际工作状态的动力学模型.

可将输入轴系统简化为以弧面凸轮的质量为质量块的弹性系统；将拨叉轴系统分别简化为以拨叉轴从动盘和拨叉的质量为质量块的弹性系统；将套筒轴系统简化为以套筒轴从动盘的质量为质量块的弹性系统；将输出轴系统简化为以刀臂的质量为质量块的弹性系统，建立双弧面凸轮机构ATC机械手的刚柔耦合动力学模型如图3所示

图3　自动换刀机构的简化动力学模型

该模型中所涉及到的符号意义如下：

θ1、θ2、θ3、θ4、θ5：凸轮、拨叉轴、拨叉、套筒轴、刀臂转角；

m1、m2、m3、m4、m5：为输入轴、拨叉轴、拨叉、套筒轴、刀臂的等效质量；

Kθ1、Kθ3、Kθ5：输入轴、拨叉、刀臂的扭转刚度；

Kec1：弧面凸轮与拨叉轴从动盘之间的等效接触刚度；

Kec2：弧面凸轮与套筒轴从动盘之间的等效接触刚度；

Cθ1、Cθ3、Cθ5：输入轴、拨叉、刀臂的扭转阻尼因子；

Cec1：弧面凸轮与拨叉轴从动盘之间的等效接触阻尼因子；

Cec2：弧面凸轮与套筒轴从动盘之间的等效接触阻尼因子；

J1、J2、J3、J4、J5：输入轴、拨叉轴、拨叉、套筒轴、刀臂的等效转动惯量；

令τ是从动盘的角位移，则当弧面凸轮的角位移为θ1时，从动盘所对应的角位移即为τ=τ(θ3)，其中τ(θ3)即为弧面凸轮所使用的运动规律.

该简化的动力学模型中只有输入轴、拨叉轴和套筒轴的扭转刚度，以及两个弧面凸轮分别与各自的从动盘滚子在工作过程中产生的等效接触刚度和拨叉与套环在工作时产生的等效接触刚度.

2.2　刚柔耦合动力学方程的建立

在动力学研究中，对于约束系统动力学问题通常都是使用拉格朗日方程来探究.因此写出该系统的拉格朗日方程如下[8]：

(1)

式(1)中：Ep为系统势能函数，Ek为系统动能函数，Ed为系统耗散函数，qi为广义坐标，Fi为广义坐标对应的广义力.

基于已完成的简化动力学模型，列出机械系统的各函数方程，并且推导拉格朗日动力学方程中各项函数.本机构最终完成简化的系统动能、势能和耗散函数如下：

(1)系统动能

(2)

(2)系统势能

(3)

(3)系统耗散函数

(4)

系统的耗散函数只考虑阻尼引起的耗散，不考虑摩擦引起的耗散，这是因为阻尼耗散较大而摩擦耗散很小，可以不予考虑.

通过拉格朗日方程对简化的系统动能、势能、耗散函数表达式进行求导，从而可以得到各个广义坐标所对应的方程，进而可以求得自动换刀机构简化后的动力学微分方程组：

(5)

3　换刀机构刚柔耦合虚拟样机的建立

要创建自动换刀机构的刚柔耦合虚拟样机，首先需要创建该机构的多刚体虚拟样机，然后再将柔性构件导入其中并完成替换，最后对其进行各种约束、接触等设置，建立机构的刚柔耦合虚拟样机.具体方法为使用ANSYS有限元软件对构件进行柔性化处理并导出“.MNF”文件，将 “.MNF”文件导入ADAMS中替换掉原有的刚体构件，之后重新对构件添加约束、驱动并进行分析.

3.1　机械手多刚体虚拟样机的建立

在ADAMS中对导入的换刀机构三维模型，选取Wstiff求解器，采用SI2积分格式，定义[9]机构材料属性，添加重力加速度，定义仿真约束，定义接触力为[Parasolids]模式；由计算得出接触参数并设置Normal Force为Impact，Stiffness为4.76E+005，Force Exponent为1.13，Damping为10.0，Penetration Depth为0.1，给机构添加驱动，建立换刀机构的多刚体虚拟样机[10].

3.2　柔性构件的选取

换刀机构的输入轴和拨叉轴以及套筒轴都属于细长轴的范围，在机构高速运行期间，由于其会受到轴上零件的惯性力、接触力以及各类负载的共同影响，会产生弹性形变，降低该机构的工作精度[11].拨叉在机构的运行过程中，容易受到自身变形、接触力以及负载作用的影响，产生弹性变形，也会对刀臂上下运动的精度产生很大影响.因此将输入轴、拨叉轴、套筒和拨叉抽象成柔性体，其他的零件仍然设置成刚体，对此刚柔耦合虚拟样机做动力学研究.

3.3　构件柔性化的过程

(1)在Creo 3.0中创建柔性体的三维模型，导出成为标准格式Parasolids文件；

(2)用ANSYS有限元软件打开该标准文件，定义构件的弹性模量为200 MPa ，泊松比为0.3，密度为7.85 g/cm3，创建的两个刚性点设置其单元类型为MASS21.将构件通过Meshing Tool划分网格，网格大小设置为3 mm；设定刚性点的MASS21单元的常实数应尽可能小，设置完成后对其进行网格划分.

(3)将做好的柔性体通过ANSYS中与ADAMS软件的接口保存成“.MNF”格式的中性文件[12]；

(4)在ADAMS中导入该柔性体，并替换掉原有刚性体，之后重新定义该柔性体的约束和驱动等.

柔性化后所得的部分结果如图4所示.

图4　凸轮轴柔性化结果

3.4　刚柔耦合虚拟样机

根据上述步骤建立的刚柔耦合虚拟样机如图5所示.

图5　替换柔性体构件后的虚拟样机

4　 双弧面凸轮式ATC机械手动态性能分析

4.1　双弧面凸轮式ATC机械手多刚体动态分析

根据前文的设置完成后，便可以做多刚体动力学仿真分析.这里把刀臂几何中心作为研究对象，作上下和回转运动的仿真分析.从动件运动规律均选取修正正弦.

由图6、图7可以看出，多刚体动力学仿真的曲线波动在升程和回程段较为集中，由于此时刀臂正在执行换刀动作.曲线整体较为平稳，机构动态性能稳定.

图6　刀臂上下运动仿真结果

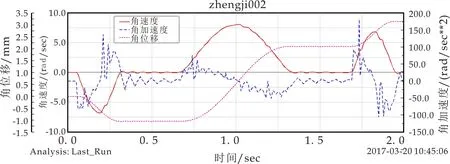
图7　刀臂回转运动仿真结果

4.2　未加负载机构动态性能分析

在没有施加轴向负载的情况下，将输入轴、拨叉轴、套筒轴、拨叉的柔性化构件导入到多刚体动力学模型中并替换各自相应的构件，与多刚体仿真分析作比较，研究其对机构动态性能的影响.

从图8可以看出，当把输入轴、拨叉轴、套筒轴和拨叉的柔性构件导入多刚体动力学模型并进行替换之后，换刀机构的刀臂在执行拔刀、插刀动作时上下运动的角位移曲线与多刚体角位移曲线完全吻合；速度和加速度曲线波动变大，不仅速度曲线的波动数量增加，而且波动幅值较大，是由于柔性构件在分析中扭转和弯曲变形较大，因此比多刚体模型的仿真曲线波动大，频率快，恰好验证了刚柔耦合动力学模型的正确性.

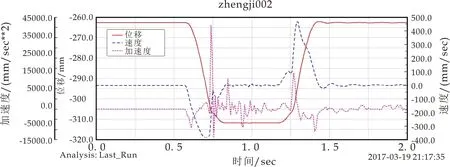
图8　替换柔性件后刀臂上下运动的仿真结果

由图9可以看出，当替换了柔性构件之后，机械手在执行换刀动作旋转180°的过程中刀臂质心处的角速度曲线图出现轻微波动，波动次数较少，角加速度曲线图出现较大波动，说明了刚柔耦合模型仿真更接近于实际情况，考虑了柔性和阻尼，因此较多刚体模型仿真曲线波动更大，频率更快，验证了模型的正确性.

图9　替换柔性件后刀臂回转运动的仿真结果

4.3　不同轴向负载对机构动态性能的影响

由于换刀机构在实际工作过程中是会受到刀具自身重力影响的，本节通过添加负载的方式来模拟刀具的重力，研究刀具重力对换刀机构动态性能的影响.为了更加接近于实际工作状态，本节选取将输入轴、拨叉轴、套筒轴和拨叉四个构件柔性化的刚柔耦合动力学模型进行研究.

自动换刀机械手在实际工作过程中，所更换的刀具的重量是不同的，所以需要考虑在不同负载下对机构动态性能的影响，由于一般刀具重量在2～8 kg之间，所以本文分别选取2 kg、4 kg、8 kg这三个工况进行研究.为了使仿真与实际情况更加接近，本文采用STEP函数来模拟刀具的重力.

该ATC机械手的外部负载STEP函数定义为[13]：

step(time,0.319,0,0.402,20)-setp(time,1.579,0,1.681,20)当需要改变负载大小时，只需将函数中的20改为40、80即可.

图10～12分别为施加负载为20 N、40 N、80 N的双弧面凸轮式自动换刀机构在执行拔刀与插刀动作时刀臂的质心位置上下移动的位移、速度和加速度曲线图.

由图10～12可以看出，在拔刀阶段，载荷刚开始施加的时候相当于一个冲击载荷，所以在此时曲线会有一个小的波动，且随着载荷的增大波动也会随之增大，但随着机构继续运行，曲线会趋于平稳，波动消失.在插刀阶段的情况基本类似，由于负载消失导致曲线有些许波动，但迅速减弱并趋于平稳.并且通过以上几幅图的对比可以看出，不同大小载荷对机构的平稳性影响并不是很大，说明该机构动态性能稳定，也证明了该机构轴向承载能力强的优点.

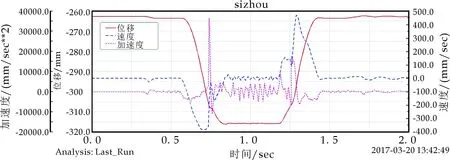
图10　载荷为20 N时刀臂上下运动的仿真结果

图11　载荷为40 N时刀臂上下运动的仿真结果

图12　载荷为80 N时刀臂上下运动的仿真结果

5　结论

本文基于Creo3.0完成了双弧面凸轮式ATC机械手三维模型的建立，并应用ANSYS和ADMAS等软件在刚柔耦合的理论基础上建立了机构的刚柔耦合动力学模型和双弧面凸轮换刀机构虚拟样机，并通过多刚体与刚柔耦合仿真对比进行了机构动态性能分析.通过柔性化对机构性能影响较大的部件，尽可能模拟了换刀机构在实际工作中的情况，验证了刚柔耦合模型的正确性，证明了该机构动态性能的稳定，对今后换刀机构的刚柔耦合分析具有参考价值.

[1] 李加明，陶卫军，冯虎田．自动换刀装置发展现状及其相关技术[J].机床与液压，2013，41(5)：174-176.

[2] 赵辉.数控机床的发展历史及其技术的发展趋势[J].内蒙古科技与经济，2007(16)：51-52.

[3] 王科社，杨庆东，孙志永.浅谈快速自动换刀装置[J].新技术新工艺，2002(10)，20-22.

[4] 董海洋.高速数控加工中心自动换刀装置机械手优化及动态测试平台检测[D].北京：北京邮电大学，2013.

[5] 王科社，杨庆东，赵宏林.高速加工中心的快速自动换刀技术[J].制造技术与机床，2001(12)：5-7.

[6] 张文光，王大镇，弓清忠.ATC中多头弧面分度凸轮实体建模与加工仿真[J].机械设计，2015，32(5)：30-34.

[7] 马志平.弧面分度凸轮机构刚柔耦合动力学研究[D].西安：陕西科技大学，2014.

[8] 郑凯，胡仁喜，陈鹿民.ADAMS2005机械设计高级应用实例[M].北京：机械工业出版社，2006：25-85.

[9] 于殿勇，钱玉进.基于ADAMS动力学仿真参数设置的研究[J].计算机仿真，2006，23(9)：103-107.

[10] Ma Qiucheng,Fang Teng.Dynamics simulation analysis of exchange cutter manipulator based on recur dyn[J].Applide Mechanics and Materials,2013,364(2):396-400.

[11] 葛正浩,张正钧,张兴钰.基于刚柔耦合模型的平行分度凸轮机构动力学分析[J].陕西科技大学学报(自然科学版),2016,34(5):142-146.

[12] 伦智达，方俊元，贾子文.基于ADAMS的刚柔耦合机器人动力学仿真[J].仪器仪表与分析监测，2012(2)：20-22.

[13] 李成平.弧面分度凸轮机构动态分析及测试系统开发[D].西安：陕西科技大学，2016.