连续电磁发射过程中轨道受力分析

张永胜， 鲁军勇， 谭赛， 李白， 武晓康， 娄建勇

(1.海军工程大学 舰船综合电力技术国防科技重点实验室， 湖北 武汉 430033；2.西安交通大学 电气工程学院， 陕西 西安 710049)

0　引言

电磁轨道发射器利用正负极两根轨道与电枢导通形成回路，在洛伦兹力的作用下将电枢组件加速至预定速度[1]。在连续快速发射模式下，轨道的长寿命技术是目前电磁轨道发射技术的最主要发展方向。而轨道应力载荷的时空分布特性是分析轨道材料失效机理和极限安全连续发射边界的前提。

针对电磁轨道发射器的热物理特性和热量管理问题，Smith等[2]和李强等[3]均基于解析法分析了轨道中的焦耳热量分布规律，林庆华等[4]利用有限元法模拟了轨道中的焦耳热量，王志恒等[5]分析了轨道中接触热的时空分布特性，Myers等[6]研究了轨道表面蒸发冷却问题，李小将等[7]分析了轨道热应力的作用特性。这些工作都没有完整给出连续发射下轨道热量的时空分布特性，也没有研究包括温度应力在内的轨道应力载荷分布特性。本文系统说明了轨道中的热量分布特性，并进一步刻画了连续发射下包括电磁力、温度应力和预紧力的多成分轨道应力载荷时空分布特性。

1　轨道应力载荷数学模型

电磁轨道发射器是特殊的机电能量转换装置，其涉及电磁场、温度场和应力场的多物理场非线性强耦合。在螺栓预紧型发射器中，轨道主要受到电磁力、温度应力和螺栓预紧力作用，3种力的时空作用规律决定着轨道的应力和应变时空分布特性。在准备发射阶段，温度应力和螺栓预紧力是轨道应力集中的影响因素；在动态发射阶段，电磁力、温度应力和螺栓预紧力是轨道应力集中的影响因素。

1.1　电磁力

电磁轨道发射器动态发射时的工作原理如图1所示[8]，在脉冲电流的作用下，轨道和电枢截面内的电流分布是不均匀的，电流主要集中分布在内表面的一个薄层中，这种效应叫做“趋肤效应”[3]。

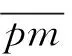
(1)

式中：ρ为材料电阻率；μ为真空磁导率，μ=4π×10-7H/m；t为从磁场开始扩散计时的时间。由轨道和电枢中的电流分布可知轨道除了受到轨道间的排斥力，还将受到电枢的电磁挤压力。

1.1.1轨道间电磁排斥力

假设电流集中于趋肤深度中分线，其中t时刻电流段ab、bc、cd、de在轨道内点p(x,-(hb+δr)/2)处引起的磁感应强度可分别计算为

(2)

(3)

(4)

(5)

1.1.2电枢的挤压力

电枢对轨道的电磁挤压力包括电枢臂受到的电磁力垂直于轨道的分量和电枢臂过盈引起的机械预挤压力[5]。电枢的挤压力计算公式[1,5]为

(6)

式中：L′为发射器电感梯度；β为电枢臂受到的电磁力垂直于轨道方向的分量转化为对轨道挤压力的系数；F0为机械预挤压力。

1.2　温度应力

电磁轨道发射器中轨道的热量来源主要有：1)轨道体电阻产生的焦耳热量；2)电枢轨道间接触电阻产生的焦耳热量；3)电枢轨道相对滑动摩擦产生的摩擦热量。取电枢运动过程中的某一时刻t1，电枢位置单位长度轨道体电阻产生的焦耳热量为

(7)

式中：ρr为轨道电阻率；hr为轨道高度；wr为轨道宽度；to为整个发射时长。

电枢轨道间接触实际上是两接触面的凸凹处在外力作用下形成的不连续斑点接触。电枢轨道间接触电阻率[9]为

(8)

式中：ρa为电枢电阻率；Hs为电枢硬度；Ac为接触面积；对于铜铝接触对，η=10.4×10-4且ζ=0.63[9]. 取电枢运动某一时间段[t1,t2]，令t2→t1，即可得到在t1时刻电枢运动单位长度电枢轨道间接触电阻产生的焦耳热量为

(9)

式中：l为接触层厚度；v(t)为电枢速度。

电枢在运动过程中，克服摩擦阻力作功产生摩擦热量。在时间段[t1,t2]内令t2→t1，即可得到在t1时刻电枢运动单位长度产生的摩擦热量[5]为

(10)

式中：μ为电枢轨道摩擦副摩擦系数。

因为轨道体电阻引起的焦耳热量在趋肤效应和临近效应共同作用下主要分布在轨道的内表面薄层，并且接触电阻产生的焦耳热量和电枢轨道相对滑动摩擦产生的热量更是从内表面传入轨道，所以轨道中热量最集中位置也是轨道受到最大温度应力位置。

2　轨道应力载荷分布特性计算

2.1　计算条件

根据第1节的推导，并且假设：1)计算电枢轨道间接触压力时不考虑电枢磨损；2)电阻率的温度系数为常量0.4%；3)电枢轨道间滑动摩擦系数在整个发射过程中保持恒值；4)电枢轨道间滑动摩擦产生的热量和接触电阻产生的焦耳热量全部传递给了轨道。数值计算用电磁轨道发射器的轨道和电枢几何模型见图2，输入参数见表1，其中wb为内膛宽度。

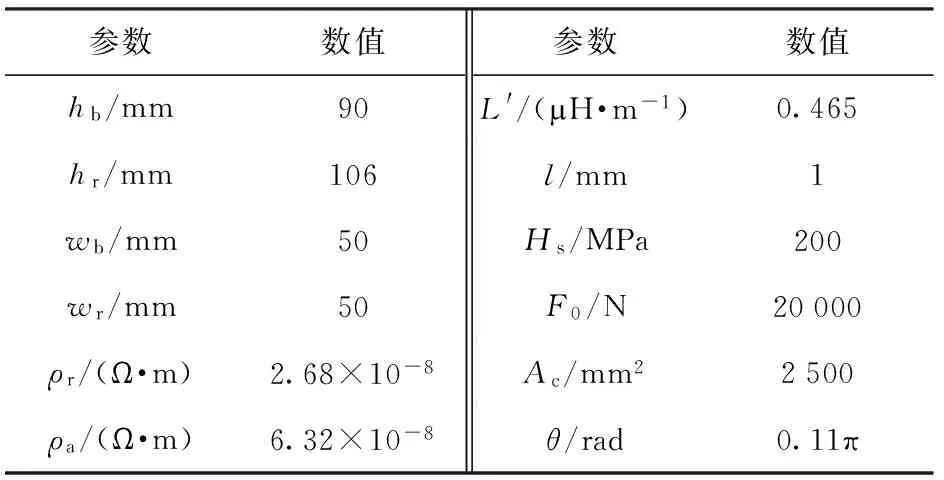
参数数值参数数值hb/mm90L'/(mH·m-1)0.465hr/mm106l/mm1wb/mm50Hs/MPa200wr/mm50F0/N20000ρr/(Ω·m)2.68×10-8Ac/mm22500ρa/(Ω·m)6.32×10-8θ/rad0.11π

在电枢的质量为2.3 kg和电枢初速为0输入条件下，得到的电流、速度和位移随时间变化关系如图3所示。其中出口速度为2 408 m/s，位移为9.88 m.

2.2　电磁力分布特性计算

本文基于有限元分析软件ANSYS Workbench的Maxwell 3D+Static Structural平台，建立了电磁场- 应力场耦合计算模型，分析了轨道受到的电磁力。结合由(1)式～(5)式建立的二维解析模型和电磁场有限元计算模型，可以得到在t=2.165 ms电枢发生400 mm位移时不同轨道位置的单位长度轨道受到的电磁力，如图4所示。因为解析过程中将轨道近似为一维线模型，故解析解大于数值解。

另外，由电磁场- 应力场耦合计算结果，电枢接触面的应力分布见图5，电枢臂长度为60 mm，其对应的轨道部分受力情况如图6所示。

由图5可知，电枢对轨道的挤压力从尾翼至肩部逐渐增大；由图6可知，轨道受到的排斥力从起始端到电枢经过位置，沿电枢运动方向也逐渐增大。另外，由(1)式～(6)式可得在时间上脉冲电流平顶沿阶段电枢经过的轨道位置受到的电磁力载荷与电流波形相似，且均基本为峰值。

2.3　温度应力分布特性计算

根据计算条件和1.2节相关理论，下面建立轨道中热量分布的三维解析模型。由(7)式可以得到轨道体电阻产生的焦耳热量随电枢位移的分布规律，如图7所示。根据(8)式和(9)式可以得到电枢轨道间接触电阻产生的焦耳热量随电枢位移的分布规律，如图8所示。由(10)式可以得到电枢轨道接触界面摩擦热量随电枢位移的分布规律，如图9所示。

从图7～图9可以看出：1)轨道中热量来源在电枢运动起始段以焦耳热量为主，之后摩擦热量的地位逐渐上升；2)接触电阻产生的热量在总热量中占比较小；3)轨道热量在脉冲电流上升段结束时刻附近电枢经过位置达到最大值，即轨道受到的温度应力载荷在脉冲电流上升段结束时刻附近电枢经过位置达到最大值。

3　轨道最大受力位置应力场的数值模拟

为抵消轨道间的排斥力，需要对身管提供紧固封装。动态发射时轨道与绝缘支撑体若发生分离，则容易使身管结构失稳，因此需要对身管施加螺栓预紧力。各轨道段受到的预紧力是相同的，并取为12 MN/m，1/4螺栓预紧型身管模型如图10所示。

由第2节可以得到，轨道在脉冲电流上升段结束时刻附近电枢经过位置受力最为严酷。本文建立了电磁- 温度- 应力多物理场耦合计算模型，假设轨道为完全弹性材料，计算得到了10发/min连续发射模式下不同时刻的轨道应力分布。以发射距离0～800 mm轨道段为对象，其中第10次动态发射电枢位移为400 mm时的轨道应力分布见图11(a)，自然冷却下第10次发射完成瞬间的轨道应力分布见图11(b)。

从图11(a)中可以看出，发射过程中最大轨道应力是由电枢电磁力引起的。从图11(b)中可以看出，自然冷却下第10次发射完成瞬间的轨道应力主要是温度应力，且在轨道边角位置取得最大值。

4　轨道冷却对轨道应力载荷的影响

冷却系统能够降低轨道的温升，通过减小轨道中的温度应力改善轨道的受力环境。喷淋冷却是电磁轨道发射器的有效冷却方式，喷淋冷却中经验对流换热系数取10 000 W/(m2·K)[6]。设环境温度为20 ℃，10发/min射击速度下连续10次发射过程中自然冷却和喷淋冷却下的轨道最高温度随时间的变化如图12所示。

第10次动态发射电枢位移为400 mm时的轨道应力分布如图13(a)所示，喷淋冷却下第10次发射完成瞬间的轨道应力分布如图13(b)所示。图13中两种工况的最大应力413.8 MPa和491.5 MPa小于图11中对应两种工况的最大应力540.2 MPa和624.1 MPa，表明喷淋冷却有效减小了连续发射过程中轨道的温度应力。

5　预紧力大小的最优化

预紧力大小影响着轨道的应力集中水平和发射时身管内膛膨胀率，预紧力越小，轨道应力集中水平越低，因此优化预紧力同样可以改善轨道的受力环境。数值模拟不同螺栓预紧力下的螺栓预紧型身管应变场，得到发射时电枢经过位置最大内膛膨胀率和轨道与支撑体间最大距离如图14所示。其中轨道与支撑体间的距离为负值表示支撑体被轨道压缩，预紧力达到12 MN/m后内膛变化率不再随预紧力的变化而变化，且此时轨道与支撑体间始终不分离。结果表明12 MN/m已为最优的预紧力，且最优的预紧力大小以恰好满足动态发射时轨道与绝缘支撑体不分离、使身管保持整体式稳定结构为判据。

6　结论

本文分析了动态发射过程中包括电磁力、温度应力和预紧力的多成分轨道应力载荷时空分布特性，所得结论如下：

1)轨道受到的电磁力载荷在脉冲电流平顶沿电枢经过位置基本上均为峰值。

2)轨道热量主要集中于电枢运动起始段，且热量密度在脉冲电流上升段结束时刻附近电枢经过位置达到最大值。

3)轨道在脉冲电流上升段结束时刻附近电枢经过位置受力最为严酷。

4)喷淋冷却可有效降低轨道中的温度应力。

5)最优预紧力以恰好满足动态发射时轨道与绝缘支撑体不分离、使身管保持整体式稳定结构为判据。

电磁轨道发射器连续发射工况的显著特征是轨道的热量累积。本文分析得到了连续发射下包括温度应力在内的轨道应力载荷时空分布特性，下一步工作将结合轨道材料的热力耦合性能和轨道的弹塑性力学，分析轨道的极限安全连续发射边界。

参考文献(References)

[1]Richard A. Marshall, 王莹. 电磁轨道炮的科学与技术[M]. 北京: 兵器工业出版社, 2006.

Marshall R A, WANG Ying. Railguns: their science and technology[M]. Beijing: Publishing House of Ordnance Industry, 2006. (in Chinese)

[2]Smith A N, Ellis R L, Bernardes J S, et al. Thermal management and resistive rail heating of a large-scale naval electromagnetic launcher[J]. IEEE Transactions on Magnetics, 2005, 41(1): 235-238.

[3]李强, 范长增, 贾元智, 等. 电磁轨道炮导轨和电枢中的焦耳热分析[J]. 弹道学报, 2006, 18(4):38-40.

LI Qiang, FAN Chang-zeng, JIA Yuan-zhi, et al. Rail and armature joule heating of an electromagnetic railgun[J]. Journal of Ballistics, 2006, 18(4):38-40. (in Chinese)

[4]林庆华, 栗保明. 电磁轨道炮瞬态温度场的数值模拟[J]. 工程热物理学报, 2017, 38(1):149-153.

LIN Qing-hua, LI Bao-ming. Numerical simulation of transient temperature field in the electromagnetic railgun[J]. Journal of Engineering Thermophysics, 2017, 38(1):149-153. (in Chinese)

[5]王志恒, 万敏, 李小将. 电磁轨道炮接触热时空分布特性分析[J]. 高压物理学报, 2016, 30(6): 511-516.

WANG Zhi-heng, WAN Min, LI Xiao-jiang. Characteristics of temporal and spatial distribution of railgun contact heat[J]. Chinese Journal of High Pressure Physics, 2016, 30(6): 511-516. (in Chinese)

[6]Myers S H, Smith A N. Demonstration of combined spray and evaporative cooling of an electromagnetic railgun[J]. IEEE Transactions on Magnetics, 2009, 45(1):396-398.

[7]李小将, 万敏, 王志恒. 电磁轨道炮轨道温度场与热应力数值仿真[J]. 火力与指挥控制, 2017, 42(2):154-158.

LI Xiao-jiang, WAN Min, WANG Zhi-heng. Numerical simulation of temperature field and thermal stress in electromagnetic railgun[J]. Fire Control & Command Control, 2017, 42(2):154-158. (in Chinese)

[8]李昕. 电磁轨道炮电枢特性理论研究[D]. 南京:南京理工大学, 2009.

LI Xin. Theoretical study on the properties of the armature in railgun[D]. Nanjing: Nanjing University of Science and Technology, 2009. (in Chinese)

[9]Hsieh K T, Satapathy S, Hsieh M T. Effects of pressure-dependent contact resistivity on contact interfacial conditions[J]. IEEE Transactions on Magnetics, 2009, 45(1): 314-315.