汽车悬架控制臂的可靠性拓扑优化∗

赵清海，张洪信，朱智富，蒋荣超，袁　林

前言

随着连续体结构拓扑优化方法的不断发展、完善和丰富，考虑不确定性因素对结构性能的影响在产品设计过程中愈来愈受到重视[1-3]。因此，基于现有的确定性拓扑优化方法，结合概率论与数理统计，给出合理的结构参数统计特征，遵从一定的设计准则规划出理想的设计方案，优化产品的性能指标，是对产品开展可靠性拓扑优化设计的基本目的[4-5]。

控制臂作为汽车悬架系统的重要零件之一，其主要功用为:通过球铰、橡胶衬套或液压衬套等元件连接车轮和车身；控制车轮相对于车身的运动特性。因此，在控制臂的结构设计中，其纵向与横向刚度和质量对车辆的操纵稳定性和平顺性有重要影响。

不同车型的动力学性能、悬架总成空间布置的多样性，往往引起控制臂结构设计空间的不确定性，且由于路况和行驶工况的复杂性以及阻尼和摩擦等边界条件的干扰，极易导致所受载荷的随机性。同时，材料的多相特征、制造工艺的差异也会引起材料属性的波动。因此，有必要在控制臂结构进行拓扑优化设计时融合可靠性分析，定量计入不确定性因素的影响。

1　确定性拓扑优化

连续体结构拓扑优化涉及静力学问题，一般可分为两类模型[6]:一为体积约束条件下最小化柔度值，即最大化刚度；二为刚度约束下最小化体积。本文中讨论刚度约束下的最小化体积问题。基于变密度法拓扑优化理论，建立数学模型:

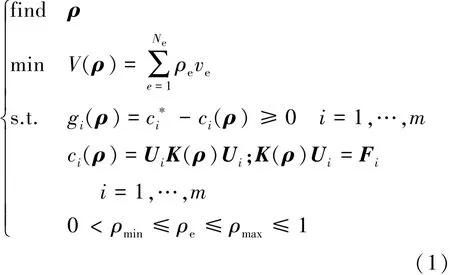
式中:ρ为设计变量矢量；V为结构体积；ρe与ve分别为单元相对密度与单元体积；Ne为设计区域单元总数；gi(ρ)为约束函数；m为柔度约束载荷工况个数；ci和分别对应第i个载荷工况下结构柔度和许用柔度值，依据结构刚度设计要求计算获得；K，Ui和Fi分别为结构的整体刚度矩阵、第i个载荷工况下节点位移矢量和载荷矢量；ρmin和ρmax分别为设计变量取值的下限和上限。

2　可靠性拓扑优化设计

2.1　可靠性拓扑优化问题变量描述

随机不确定性变量主要表现在结构的材料属性、载荷的随机性，适用于采用概率论描述其分布特征[7]。

以变密度法为例，确定性变量表征单元相对密度ρ为拓扑优化设计变量。随机变量X＝[x1，x2，…，xd]表征结构不确定性因素，为连续型变量。一般将非正态分布随机变量进行标准化处理转换为相互独立的标准正态随机变量U＝[u1，u2，…，ud]。变量U服从均值为0、标准差为1的标准正态分布，记为 N(0，1)。

2.2　可靠性拓扑优化数学模型

基于可靠性拓扑优化问题变量界定，典型的可靠性拓扑优化数学模型可描述为

式中:Gi(·)为第i个极限状态函数或功能函数；Pr[·]为失效概率；Pfi∗为许用失效概率值。在结构可靠性分析中，该功能函数定义的极限状态为:Gi(ρ，X)＝ 0；即随机变量空间中安全区域(Gi(ρ，X)≥0)和失效区域(Gi(ρ，X)≤0)的分界面。图1展示了确定性最优与可靠性最优的区别。

图1　确定性最优和可靠性最优示意图

假设随机变量X相互独立，失效概率Pr[Gi(ρ，X)≤0]可通过多维积分计算得到:

式中fX(x)为X的联合概率密度函数。失效概率积分计算的前提是需已知联合概率密度函数和功能函数。目前主要采用蒙特卡洛法、一次二阶矩法[8]与一次可靠度法等[9]近似计算失效概率。

2.3　可靠性拓扑优化-解耦格式

由式(2)可靠性拓扑优化数学模型可知，其求解过程一般包含:针对随机变量的可靠性分析和针对设计变量的结构拓扑优化。目前，基于可靠性的结构拓扑优化设计方法主要采用双层嵌套格式。该方法的主要缺点是计算量大，计算效率低且收敛困难，因此其广泛应用受到限制。为此，提出可靠性拓扑优化-解耦格式，即将问题分解为可靠性分析和等价的确定性拓扑优化两个独立子问题分别进行求解。具体流程为:首先根据一次可靠度法中可靠性指标的几何意义，寻求满足目标可靠性指标的设计点，然后依据随机变量的灵敏度信息进行随机变量修正，从而将可靠性约束条件转化为等价的确定性约束条件，最后进行确定性拓扑优化。对于确定性优化问题，可以直接借助现有的成熟软件优化求解器进行求解。具体的优化流程如图2所示。

根据一次可靠度法，失效概率约束可转化为可靠性指标约束:式中:βi和 βi

∗分别为第i个失效概率的可靠性指标和许用可靠性指标。遵循结构可靠性指标的几何意义[5]，结合可靠性指标约束，构建关于正态随机变量的优化模型:

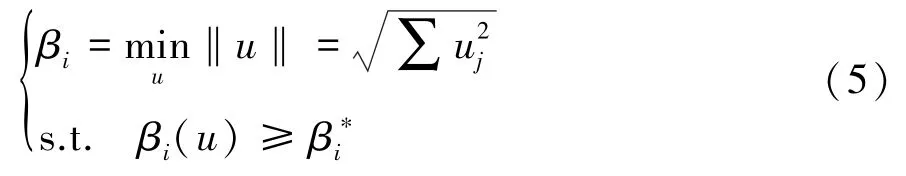
其中，结构可靠性指标相对于正态随机变量的灵敏度可解析为

该模型的最优解u∗称为设计点。根据Rosenblatt逆变换[10-11]，获得随机变量的修正值:

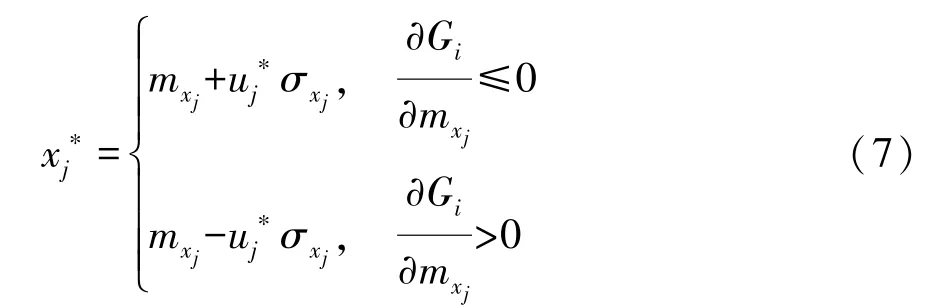
其中 i＝1，…，m；j＝1，…，n

图2　可靠性拓扑优化-解耦格式示意图

式中:mxj和σxj分别为随机变量xj的均值和标准方差。而功能函数相对于随机变量均值的灵敏度信息可通过有限差分法近似求得:

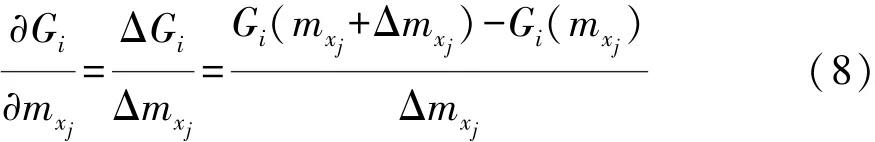
通常取步长 Δmxj＝0.01mxj。

基于随机变量的修正值，将可靠性优化转化为等价的确定性拓扑优化问题:

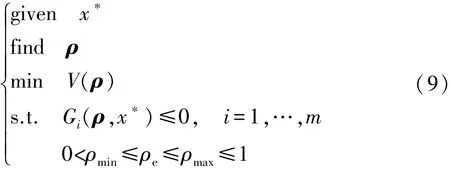
3　控制臂算例分析

以某汽车悬架系统的下控制臂为例，考虑结构的材料属性与载荷工况的不确定性，根据控制臂的结构特点与装配关系定义初始设计空间，如图3所示。其中，控制臂与球铰和橡胶衬套的连接部位设置为非设计区域。采用刚性单元(RBE2)模拟球铰或橡胶衬套与控制臂之间的装配接触。位移自由度约束设置为:约束后衬套节点处沿X，Y，Z方向的平动自由度、前衬套节点处沿X，Z方向的平动自由度和控制臂球铰节点处沿Z方向的平动自由度。在控制臂球铰节点处施加纵向力Fx和侧向力Fy两个载荷。控制臂材料属性与载荷工况设置见表1。

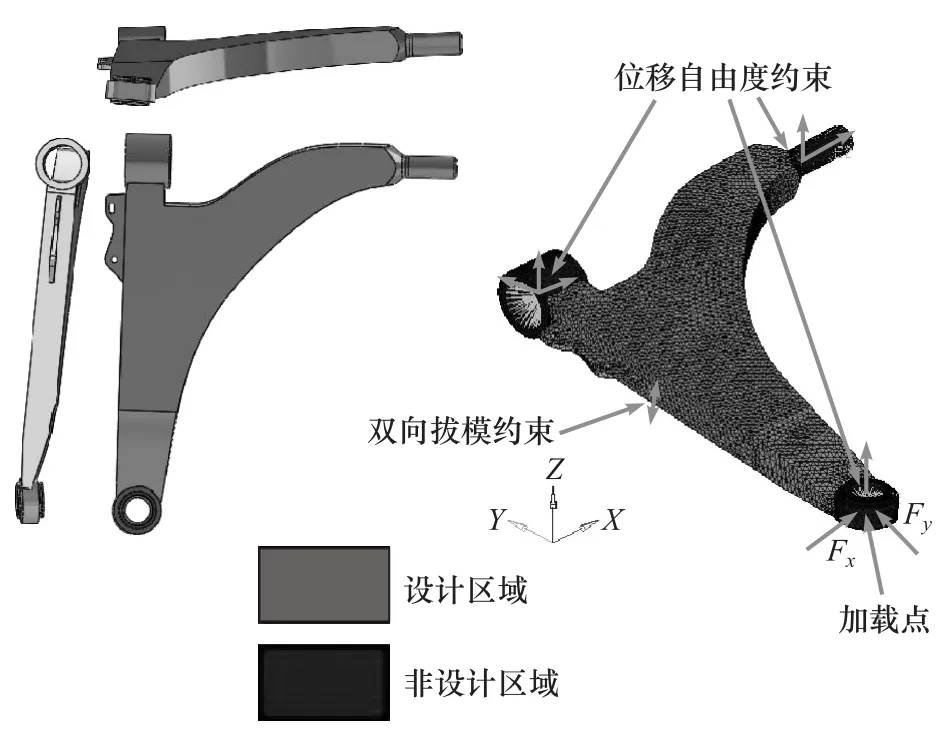
图3　控制臂的设计空间

对于确定性拓扑优化，结构柔度约束条件，即许用柔度值，纵向力工况时为c1∗＝2.9×103N·mm；侧向力工况时为c2∗＝5.0×104N·mm。制造工艺性约束设置为最小成员尺寸约束与双向拔模约束。得到的确定性拓扑优化材料分布如图4所示，其中，拓扑构型密度阈值设置为0.30。

图4　控制臂材料分布方案(确定性设计)

表1　控制臂的材料属性与载荷工况(均值)

对于可靠性拓扑优化，可靠性指标约束设置为3，4，5。随机变量选取为弹性模量E、纵向力Fx和侧向力Fy，其中变量满足正态分布，设置标准差为σ＝0.10m，m为随机变量的均值。可靠性拓扑优化结果如图5所示，密度阈值设置为0.30。确定性拓扑优化结果与可靠性拓扑优化体积目标迭代曲线如图6所示。采用可靠性分析-解耦格式，计算结果汇总于表2。

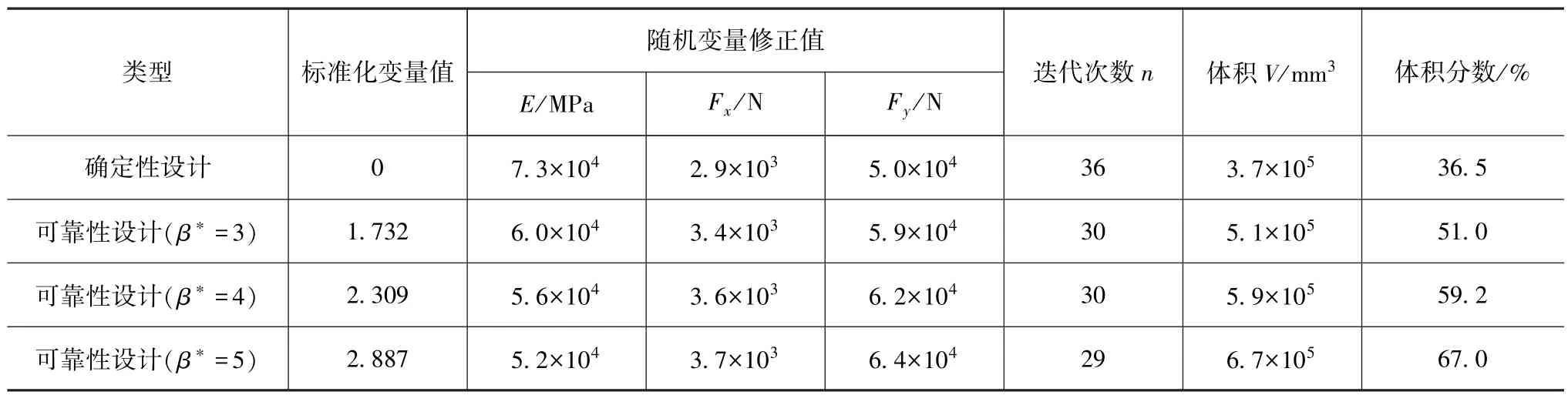
表2　确定性与可靠性拓扑优化设计结果

通过对比确定性和可靠性优化结果可以看出，基于可靠性的拓扑优化结果需要更多的材料分布构型，以便满足可靠性指标约束要求，且材料分布均匀，具备良好的可制造加工性，结果更趋于合理。

由表2可知:依据可靠性指标可方便进行随机变量修正，且只需要几十次迭代优化计算即可获得良好的拓扑构型；相较于确定性拓扑优化算法，计算速度更快，计算效率更高。对比确定性与可靠性优化结果目标函数体积，以β∗＝3为例，体积相对增加37.8%，表明结构可靠性的提高有可能伴随结构体积的增大。

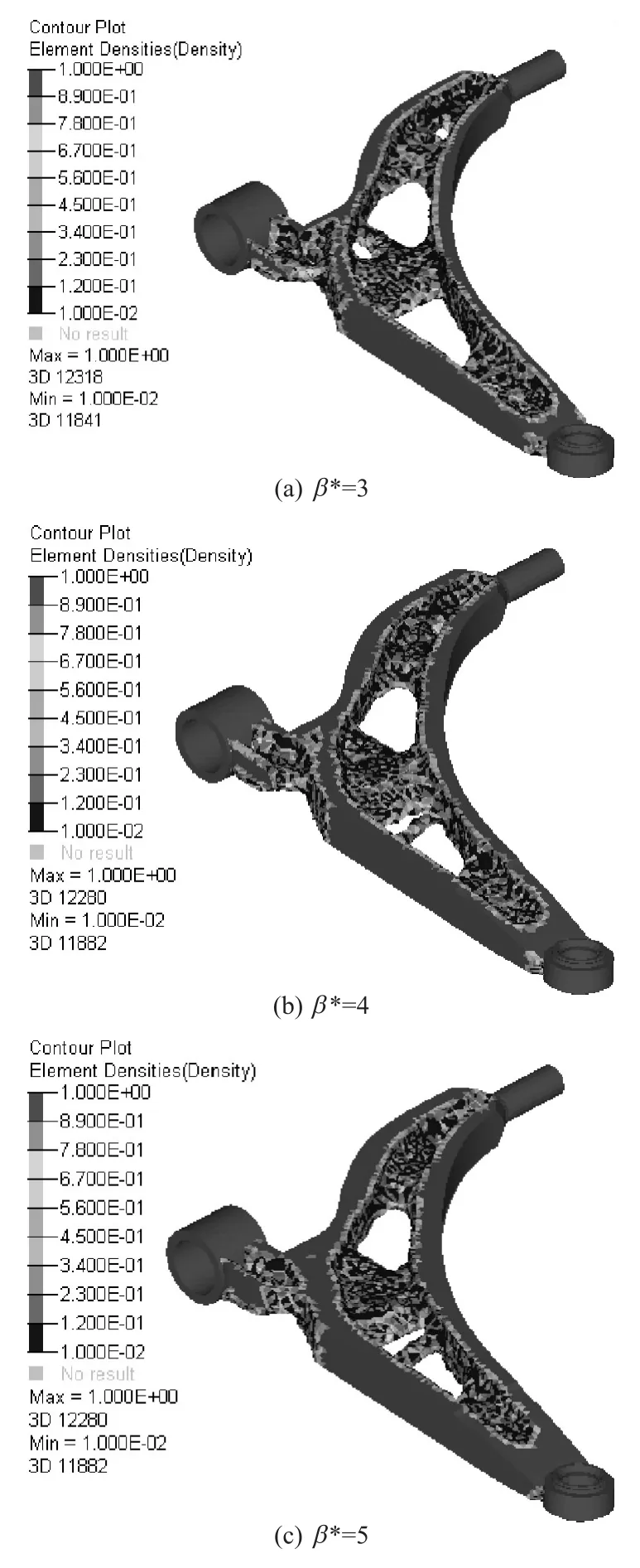
图5　控制臂材料分布方案(可靠性设计)

图6　控制臂结构目标体积收敛迭代曲线

根据可靠性拓扑优化设计结果(β∗＝4)，并考虑制造工艺条件、空间布置要求以及设计准则，并且对控制臂结构细节部位尺寸、形状进一步优化的基础上，经过详细设计后的控制臂结构如图7所示。其中确定性模型与可靠性模型质量分别为1.523和1.545kg。

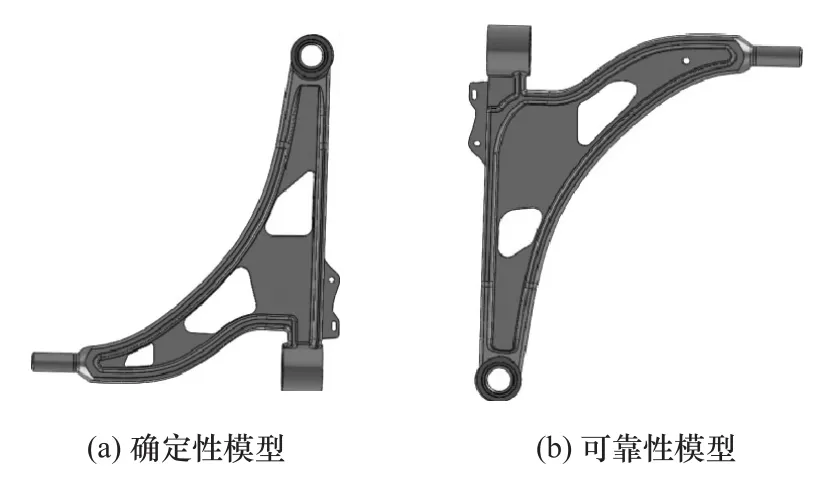
图7　可靠性拓扑优化设计模型重构

依据最终设计方案，对新控制臂结构进行有限元分析验证，计算结构刚度及动力学性能，并与确定性控制臂结构进行性能对比。控制臂确定性与可靠性拓扑优化设计刚度分析如图8所示。

图8　控制臂可靠性拓扑优化设计刚度分析

为了验证控制臂模型仿真结果的有效性，开展刚度试验。试验测试系统包括力传感器、直线导轨和百分表等。测试台架如图9所示。控制臂确定性模型与可靠性模型刚度试验所得载荷-位移曲线如图10所示。

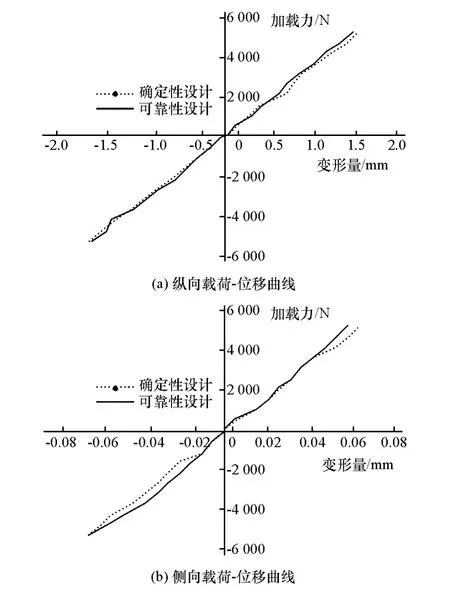
图10　控制臂模型刚度载荷-位移曲线

计算仿真与试验测试结果表明:确定性设计与可靠性设计均能满足性能设计要求。结构在纵向和侧向载荷工况作用下，纵向位移和侧向位移均小于1mm，满足刚度性能；并且仿真验证与试验校核结果相吻合，控制臂纵向刚度和侧向刚度分别提升3.8%和7.5%，结构在受力时抵抗弹性变形的能力得到增强。

控制臂结构模态对整车NVH性能起着至关重要的作用，因此对其进行模态分析，其1阶模态振型如图11所示。

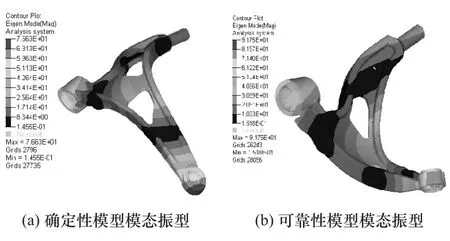
图11　控制臂模态分析(1阶模态)

进行控制臂模型模态试验，用弹性绳悬挂方式模拟被测样件的自由状态，测试系统包括激励系统、响应拾振系统及模态分析和处理系统3大部分。控制臂模态试验台架如图12所示。控制臂模态分析仿真与试验结果汇总于表3。

图12　控制臂模态试验台架

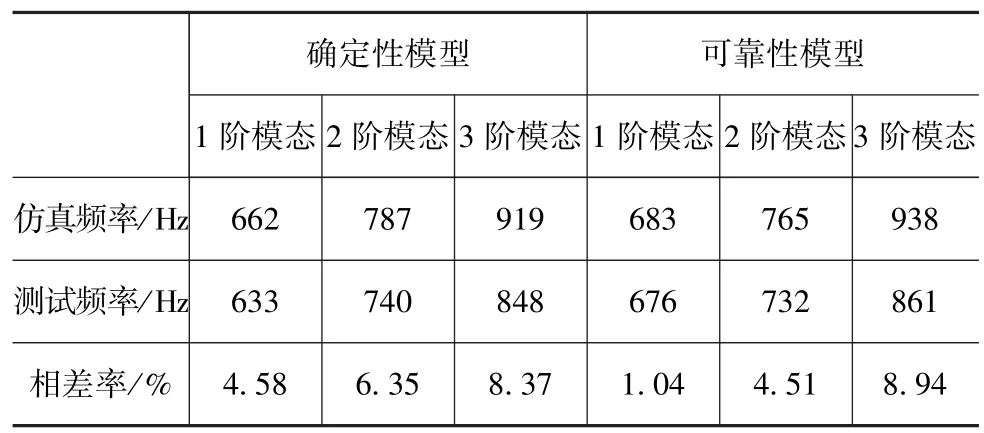
表3　控制臂模态分析结果(前3阶)

模态结果表明:确定性设计与可靠性设计控制臂结构1阶频率均大于600Hz，满足NVH性能。可靠性设计结果的1阶模态比确定性设计高3%左右，从而降低发生共振现象的概率，有效避免结构疲劳破坏的出现。因此，确定性拓扑优化设计和可靠性拓扑优化设计均能满足控制臂结构设计性能需求，而后者性能更优。结果表明:与确定性优化结果相比，可靠性拓扑优化结果能在不过多增加结构质量的前提下，显著提高了结构的静力学与动力学性能，能适应良好的载荷不确定性的影响，增强了结构工作的可靠性，避免由于参数变动引起结构性能的波动甚至结构失效的发生。

4　结论

由汽车控制臂的可靠性优化设计算例结果可得，本文中提出的方法通过求解符合满足可靠性指标的标准化变量值，完成随机变量的修正，进而进行等价的确定性拓扑优化，避免了优化过程中繁琐的可靠性分析，从而大大缓解了可靠性优化的计算负担。所提出的优化算法不仅能获得优良的可靠性拓扑优化构型，且能通过合理修改结构的参数值，获得指定的可靠性指标。因此，所提出的方法具备良好的实用价值，可最大限度地满足经济性和安全性的设计要求。

[1] 陈小前，姚雯，欧阳琦.飞行器不确定性多学科设计优化理论与应用[M].北京:科学出版社，2013.

[2] 乔升访，周克民.基于类桁架材料模型的不确定荷载下结构拓扑优化[J].工程力学，2016，33(1):252-256.

[3] 刘国梁，陈建军，马洪波.一种基于非概率可靠性的结构水平集拓扑优化[J].工程力学，2012，29(6):58-62.

[4] ZHAO Q H，CHEN X K，MA Z D，et al.A comparison of deterministic，reliability-based topology optimization under uncertainties[J].Acta Mechanica Solida Sinica，2016，29(1):31-45.

[5] ZHAO QH，CHENX K，MA ZD，et al.Reliability-based topology optimization using stochastic response surface method with sparse grid design[J].Mathematical Problems in Engineering，2015，Article ID:487686.

[6] BENDSØE M P， SIGMUND O.Topology optimization:theory，methods and applications[M].Berlin:Springer，2003.

[7] AOUES Y，CHATEAUNEUF A.Benchmark study of numerical methods for reliability-based design optimization[J].Structural and Multidisciplinary Optimization，2010，41(2):277-294.

[8] LEE SH，CHEN W.A comparative study of uncertainty propagation methods for black-box-type problems[J].Structural and Multidisciplinary Optimization，2009，37(3):239-253.

[9] HASOFER A M，LIND N C.An exact and invariant first order reliability format[J].ASCE Journal of Engineering Mechanics，1974，100(1):111-121.

[10] ROSENBLATT M.Remarks on a multivariate transformation[J].Annals of Mathematical Statistics，1952，23(3):470-472.

[11] LIU P L，KIUREGHIAN A D.Multivariate distribution models with prescribed marginals and covariances[J].Probabilistic Engineering Mechanics，1986，1(2):105-112.