基于粒子群算法的轿车车身多学科优化设计∗
刘 钊,李 晗,朱 平
前言
轿车车身结构设计是一个集汽车碰撞安全性、振动、噪声和舒适性为一体的复杂系统优化设计问题。在其设计过程中,设计变量多、非线性程度强,学科间耦合关系复杂,常用的多学科优化策略和优化算法无法有效寻得可行的优化解。
为有效解决车身多学科优化设计问题,国内外学者进行了一系列的探索。文献[1]中在同时考虑材料替换、碰撞性能和NVH约束的情况下对镁材料车身结构进行了多学科优化设计,并运用SQP进行序列求解,获得材料替换后较为优异的车身零部件厚度分布。文献[2]中提出基于近似建模技术的解决大规模工程问题的多学科优化流程,并将其运用到整车结构开发流程中,显示了该方法的先进性。文献[3]中针对一款商用车身首先进行拓扑概念设计,然后进行基于近似模型的多学科结构变量优化设计。采用全局灵敏度分析方法来减少整体结构优化变量的个数,通过算例分析证明其多学科优化设计流程的可行性。文献[4]和文献[5]中结合协同优化与多目标遗传算法,综合考虑侧撞安全、白车身模态和静态弯曲刚度等性能响应进行车身结构轻量化设计。文献[6]中通过多学科优化过程找到白车身零件形状、尺寸、位置和厚度各参数间的最佳组合。文献[7]中运用协同优化方法,结合可靠性优化方法提高优化结果的可靠性。文献[8]中考虑自卸车货箱线性静力和振动模态,运用多学科优化设计方法进行轻量化设计。文献[9]中针对汽车转向盘骨架性能进行结合协同优化和近似建模技术的性能优化设计。
由国内外学者的研究可知,多学科优化设计在汽车中的应用灵活,常采用近似建模、变量筛选和灵敏度分析等方法来降低问题复杂程度。一体式优化方法运用较多,因其避免了学科间共享变量的处理问题,但子学科自主性较差,无法针对各子学科特点进行相应的优化处理,基于两步式的多学科优化方法如协同优化算法有待研究。此外,优化算法选择单一,虽有提及优化算法求解问题,但并未针对单独子学科进行考虑学科特点的优化运算。本文中针对车身多学科优化设计问题,提出基于灵敏度分析的数据挖掘技术,辨识问题的优化区域,形成考虑优化问题特点的粒子群算法流程,有效提高了粒子群优化算法解决约束优化问题的能力,结合加强多学科协同优化理论,形成了基于改进粒子群算法的轿车车身多学科优化设计体系,并通过实际工程案例验证了该方法的有效性。
1 约束条件下的粒子群优化算法
1.1 粒子群优化算法
粒子群优化算法是一种基于群体智能的进化计算(evolutionary computation)技术,其思想来源于人工生命和进化计算理论。粒子群优化算法是以模拟鸟群的群体智能为特征,以求解连续变量优化问题为背景的一种优化算法,最早由Kennedy等学者受到鸟群觅食行为的启发而提出[10]。粒子群优化算法采用实数求解,且需要调整的参数少,易于实现,是一种通用的全局优化算法。
1.1.1粒子群优化算法的基本形式
基本的粒子群优化算法中,粒子群由m个粒子组成,每个粒子的位置代表一个优化问题在n维搜索空间中的潜在的优化解。粒子根据以下3条规则来更新自己的状态:保持自身惯性、按自身的最优位置来改变状态和按照群体的最优位置来改变状态。
通常粒子群算法的数学描述为:假设在一个n维的搜索空间中,由m个粒子组成的种群χ={x1,x2,…,xm},其中第 i个粒子的位置为 xi= (xi,1,xi,2,…,xi,n)T,其速度为 vi=(vi,1,vi,2,…,vi,n)T。个体极值为 pi=(pi,1,pi,2,…,pi,n)T,种群的全局极值为pg=(pg,1,pg,2,…,pg,n)T。 粒子在找到上述两个极值后,就根据速度更新公式和位置更新公式来更新自己的速度和位置:

式中:c1和c2为学习因子或加速常数;r1和r2为介于[0,1]之间的随机数;vki,d和 xki,d分别为粒子 i在第 k次迭代中第d维的速度和位置;pki,d为粒子 i在第 d维的个体极值位置;pkg,d为群体在第d维的全局极值的位置。
1.1.2粒子群优化算法流程
粒子群优化算法流程如图1所示。

图1 标准粒子群算法流程图
1.2 约束处理方式分析
粒子群优化算法优化过程中模拟鸟群觅食行为可有效地寻得全局最优解,效率高、稳定性好。但其开发初期主要针对无约束优化问题,而现实的工程问题多为约束优化问题,约束的引入会对优化进程产生较大的影响,进而影响该方法的应用。粒子群算法优化过程中常用的两种约束为边界约束与函数约束。
1.2.1边界约束
边界约束是指优化问题给定的设计变量寻优范围。如果一个优化问题含有边界约束,当粒子运动处于设计边界外时需要进行适当的处理,特别是那些优化解处于靠近边界的可行区域内的问题,边界约束的处理方式对其优化求解影响较大。文献[11]中系统性地研究了不同的边界约束处理方法,通过大量的数学实验分析,得出边界反射方式与粒子速度赋值为0适用于大多数测试函数。边界反射处理方法(reflect method)将位置在设计域以外的粒子基于设计边界反射回到设计域内,其原理如图2所示。

图2 边界反射方法
1.2.2函数约束
函数约束在实际优化问题中经常遇到,其处理方式的选择对优化问题的求解有较大的影响。目前,惩罚函数方法在约束问题处理中运用最为广泛,其主要思想是将优化问题的约束函数进行转换,形成一系列的无约束优化问题。本研究中采用最普遍的非静态惩罚函数法来处理约束优化问题[12]。
通常包含惩罚函数的方程为

式中:f(x)为约束优化问题的初始目标函数;h(k)为惩罚修正值,k为当前的代数;H(x)为惩罚因子。

式中:qi(x)= max{0,gi(x)},i= 1,…,m;θ(qi(x))为多级分配函数[13];γ(qi(x))为惩罚函数的指数;gi(x)为惩罚函数。
本文中惩罚函数的参数设置与文献[12]中相同。 若 qi(x)<1,则 γ(qi(x))= 1,否则 γ(qi(x))=2。 若 qi(x)≤0.001,则 θ(qi(x))= 10;若 0.001<qi(x)≤0.1,则 θ(qi(x))= 20;若 0.1<qi(x)≤1,则θ(qi(x))= 100;若 qi(x)>1,则 θ(qi(x))= 300。 优化问题中h(k)=k k。
1.3 基于灵敏度分析的优化域识别方法
对于复杂的工程实际应用问题,其优化数学模型的形态复杂,优化求解困难,优化结果精度达不到要求。目前一般的算法对优化初始位置的摄取依赖性较大,对于高维复杂工程优化问题,特别是车身碰撞工况这种强非线性的复杂优化问题,传统优化算法难以获得有效全局最优解,需要采用先进优化算法进行寻优求解,而为获得更好的效果,须进行相应粒子群位置的优化。
1.3.1灵敏度分析技术
为得到初始求解合理的粒子分布区域,需要针对具体的问题的优化目标,运用分类与回归树(CART)数据挖掘技术针对可行的优化区域进行辨识。通过灵敏度分析可决定参数对系统或模型的影响程度。目前最常用的全局灵敏度分析方法为Sobol法。
Sobol灵敏度分析方法是一种基于方差的蒙特卡罗方法。定义一个k维的单元体Ωk作为输入变量(因素)的空间域:

Sobol方法的核心思想是将函数f(x)分解为子项之和:
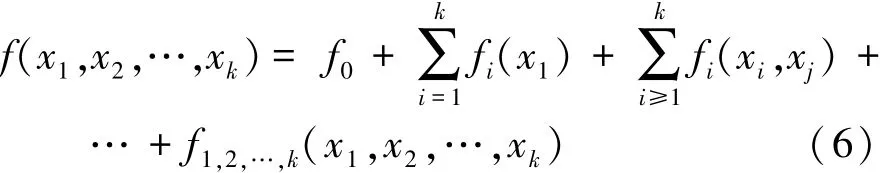
根据统计学相关知识,模型输出f(x)的总方差为

各阶子项的方差称为各阶偏方差,即s阶偏方为
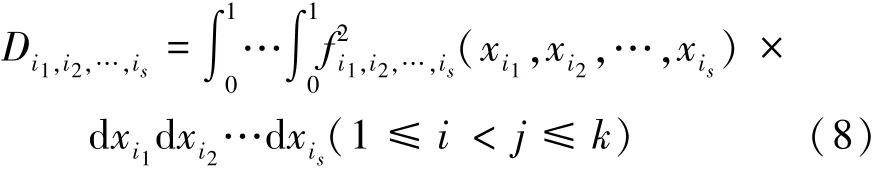
总方差等于各阶偏方差之和:

将各阶灵敏度系数定义为各阶偏方差与总方差的比值,则 s阶灵敏度 Si1,i2,…,is为
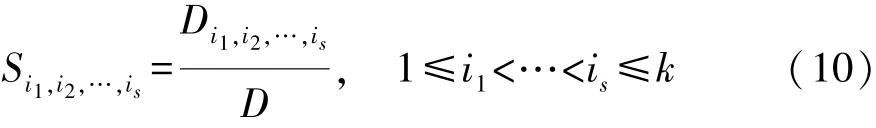
式中:Si为因素xi的1阶灵敏度系数,表示xi对系统输出的主要影响;Sij(i≠j)为2阶灵敏度系数,表示两因素之间的相互影响;依次类推,S1,2,…,k为 k 阶灵敏度,表示k个因素之间的相互作用。
在Sobol灵敏度分析方法中,各积分可由蒙特卡罗法求出。因此f0,D和Di可通过蒙特卡罗估计求得:

1.3.2基于灵敏度分析的优化域识别流程
针对约束优化问题影响主因的数据挖掘流程如图3所示。

图3 基于灵敏度分析的数据挖掘方法
具体步骤如下:
(1)针对具体的实际工程优化问题,进行设计域内的最优拉丁超立方采样,采样技术选择基于加强进化算法的最优拉丁超立方采样技术,采样规模根据实际工况的设计变量个数与问题复杂程度进行;
(2)对实际问题进行有限元仿真分析,输入步骤(1)中的采样数据,输出为优化目标和约束的响应值;
(3)运用步骤(1)和(2)中获得的问题输入与输出建立近似模型,验证模型精度,如不满足则通过序贯采样技术进行近似模型精度提升;
(4)基于满足精度要求的近似模型进行灵敏度分析,获得影响问题响应的主要设计变量;
(5)针对优化问题的主要影响变量,运用分类与回归树数据挖掘方法(CART)进行数据挖掘,获得问题的优化设计区域。
1.3.3考虑优化问题特点的粒子群分布控制方法
为能针对具体的优化问题进行更好的寻优求解,开发出考虑优化问题特点的粒子群分布控制方法。主要思想是在通过数据挖掘方法进行设计域分析的基础上,进行初始粒子群位置的布置。本部分初始粒子群主要由两部分组成:第一部分采用最优拉丁超立方采样的方法,保证了粒子群对优化设计空间的覆盖;第二部分粒子主要分布在由数据挖掘技术分类出的优化区域,该区域考虑了影响问题的主因,通过针对主要设计变量进行相应的数据挖掘,获得与具体优化问题相适应的分类区域。随后运用粒子群优化算法进行寻优运算,具体流程见图4。
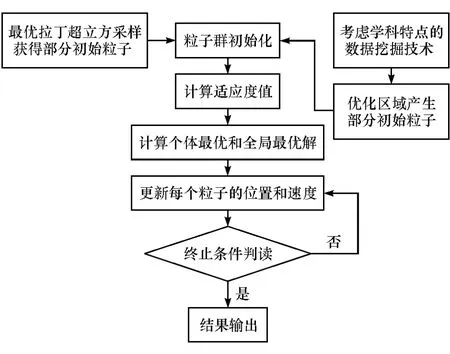
图4 考虑学科特点的粒子群方法
该方法通过对设计域的初始探索,更有效地指导粒子在设计空间中的分布,在保证了粒子对整个设计域探索的同时,重点将粒子分配在可能的优化区域,进而提高粒子种群针对特定优化问题的探索能力,提升粒子群算法的寻优精度。
2 加强协同多学科优化方法
传统的协同优化方法(CO)开发以来,已被成功运用在航空航天和交通运输等领域,但其在求解过程中会遇到诸如存在奇异解、不收敛等缺陷。因此,文献[14]中提出加强协同优化算法(ECO)[14],该算法的核心思想是将各子系统之间的约束模型进行相互共享,在一个子系统优化过程中,考虑到其余子系统对该子系统的影响,这样可以避免子系统级优化时为了寻找合适的共享变量造成的求解困难。ECO方法针对系统级优化和子系统级优化结构进行了相应的修改。
系统级优化器一般的表达形式为

式中:z为系统级赋予共享变量的目标值;x∗为子系统优化过程中寻得的与系统级优化目标最接近的问题解。原始的协同优化算法为各子学科级的优化提供了很大的学科自由度,每个子系统可根据自己的学科特点选择相适应的优化技术。但每一个学科对其余子学科的学科特点和优化偏好并不清楚。各子学科之间信息的传递只能通过主系统进行间接传递,这就要求系统级优化器需要承担共享变量的选择任务。子系统级优化器承担大部分的设计决策任务,其目标函数包含3个部分:系统优化目标的二次方程、检验兼容性的二次方程和一系列的松弛参数。其约束包含子系统局部约束和由于其余学科的耦合关系而产生的约束。子系统接收由主系统传递的目标(z)和作为参数的约束模型系数(∂g(j)/∂xs)。子系统反馈响应目标(x∗s),子系统级优化器数学表达为
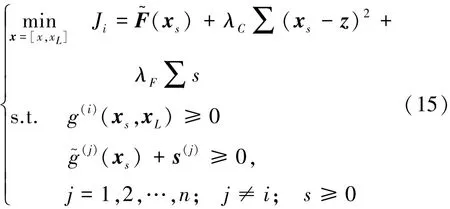
式中:x为子系统独立的共享变量;xL为局部变量;xs=[x,y]为与多个子系统相关的共享变量;y为耦合变量;s为松弛系数,保证子系统问题求解的可行性;z为参数,由系统级优化器提供,作为子系统目标;λC为兼容性惩罚系数;λF为可行性惩罚系数;F~为问题目标的二次方程组模型;g(i)为子系统i的局部约束;g~(j)为子系统j的线性约束模型。
3 车身侧围结构轻量化设计
车身侧面结构相对简单,在碰撞过程中,其结构的变化将直接影响到乘员舱内驾乘人员的生命安全,因此侧面碰撞工况是其设计时需要重点考虑的一个工况。同时侧围结构对整车的刚度模态变化影响较大,因此也需要在设计时进行重点考核,所以在车身侧围结构设计时需要同时考虑碰撞工况和车身刚度模态工况,是一个典型的多学科优化问题。本文中将选它作为应用案例,结合协同多学科优化设计方法,验证研究中提出的考虑优化问题特点的粒子群分布控制方法的合理性和实用性。
3.1 优化设计问题
整车侧面碰撞有限元模型包含详细的白车身、底盘和动力总成有限元模型,单元平均尺寸为10mm,壳单元1 005 019个,实体单元22 575个,梁单元7 718个。轿车侧面碰撞仿真模型如图5所示。

图5 侧面碰撞仿真模型
根据GB 20071—2006《汽车侧面碰撞的乘员保护》的法规要求,质量为950kg的移动壁障车以50km/h的速度呈90°冲击轿车驾驶员侧,移动壁障车的对称中面通过驾驶员座椅的R点,仿真时间为80ms。考虑的性能指标为:假人下肋骨最大变形量、B柱最大变形速度、车门最大变形速度、假人腹部作用力、假人盆骨作用力。选取与侧面碰撞最相关的车身侧面15个板件的厚度作为设计变量,如图6所示。

图6 侧面碰撞设计变量
建立考核车身刚度和模态的白车身有限元模型,如图 7所示,白车身骨架共有 275个零件,351 722个单元,其中三角形单元15 851个,占单元总数比例4.51%,根据有限元网格划分规则,可知建立的车身骨架有限元模型精度可靠,可用于后续的仿真运算。
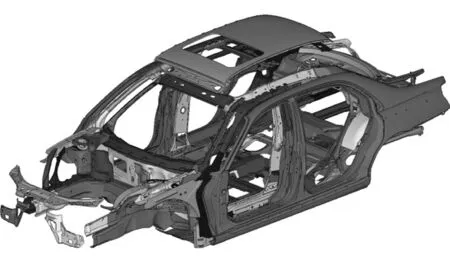
图7 刚度、模态优化设计变量
车身刚度包括弯曲刚度和扭转刚度两个指标,主要研究白车身结构在受到外界载荷作用下结构抵抗变形的能力。对于车身刚度和模态工况来说,设计变量较多,为降低运算成本,运用灵敏度分析技术获得其设计变量中影响较大的20个变量作为优化设计变量进行后续的优化运算。
综合车身侧面碰撞工况和车身刚度模态工况的几种性能指标,具体指标和约束要求如表1所示。基于验证后的仿真模型,进行针对每一个碰撞工况的优化设计域识别。首先是针对仿真工况进行近似模型建模。根据各自工况的设计变量个数进行最优拉丁超立方采样,建立与之相对应的近似模型,并验证模型精度,获得满足精度要求的数学模型。其中,侧面碰撞工况设计变量15个,训练样本120个,测试样本20个;白车身刚度和模态工况设计变量20个,训练样本100个,测试样本20个。

表1 工况描述
根据加强协同多学科优化方法,建立两学科系统。本例中优化目标为质量最小,优化目标可方便地分配到各个子学科,且各学科间只存在共享变量,不存在状态变量(学科间耦合变量),因此问题的形式比较明确。
系统级优化主要平衡学科间的一致性,其形式为
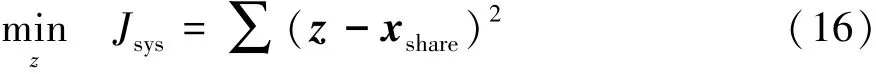
在子学科系统中,共享变量有两个,子系统目标形式需加入保证学科一致性的多项式,子系统优化问题的数学模型如下。
(1)侧面碰撞

式中:Mside(xs)为侧面碰撞工况轻量化分目标;λC∑(xside_s-z)2为一致性约束条件。其约束为侧面碰撞工况中需要考虑的各约束指标。
(2)车身刚度和模态

式中:Mstiff(xs)为侧面碰撞工况轻量化分目标;λC∑(xstiff_s-z)2为一致性约束条件。其约束为车身刚度和模态工况中需要考虑的各约束指标。
3.2 优化问题设计域识别
基于近似模型,建立灵敏度分析目标值:

运用灵敏度分析技术,分析每个碰撞工况中影响优化问题的主要变量,约束函数因子λ取值均为1。经分析后各工况选取灵敏度排序前5的设计变量如表2所示。

表2 各工况灵敏度分析
3.3 优化与结果分析
本文中提出的多学科优化运用加强协同优化算法进行各个学科耦合关系的构建,运用基于灵敏度的数据挖掘技术进行优化区域辨识,通过合理布置粒子进行基于粒子群优化算法的寻优求解。因本算例中考虑到碰撞和刚度模态两个学科,对于碰撞工况来说,其优化非线性强,寻优相对困难,故基于多样性保持机制的改进粒子群算法策略[15];而对于刚度和模态工况,因其优化问题非线性程度较弱,相对易于求解,故采用标准粒子群算法流程。实验算例定义为算例1,为验证本例运用多学科优化方法结构的优势,设计算例2和算例3两种对比算例。算例2同样运用考虑学科特点的优化域挖掘技术,与算例1算法结构相同,但在优化算法选择上各子学科均采用标准粒子群算法。算例3中在优化运算时不采用优化域挖掘的方法,仅用加强协同优化算法结构,优化求解方法运用标准粒子群算法。
对3种算例结构进行寻优求解,为将数学求解结果转换为实际工程中可以运用的板厚,对优化结果进行圆整。将圆整后的结果输入到仿真软件中进行分析,验证结构设计结果的正确性。结果如表3所示,算例1完成减质量12.6kg,减质量效果为14.6%;算例2完成减质量 8.1kg,减质量效果为9.4%;算例3完成减质量6.16kg,减质量效果为7.1%。通过对比验证了本文中提出的多学科优化构架在实际工程中寻优求解的优势。

表3 各算例轻量化方案的性能指标状态
4 结论
(1)针对车身结构多学科优化设计问题,研究了其耦合结构与优化算法运用两个问题。分析其多学科之间的耦合关系,运用加强协同多学科优化策略,系统级优化主要解决学科一致性问题,各子系统承担部分问题的优化目标,并通过目标和约束修正考虑不同学科之间的耦合关系,保证学科间的一致性。
(2)考虑不同学科优化问题特性不同,针对具体的问题进行基于灵敏度分析的数据挖掘,获得问题的优化区域,进而指导粒子群优化算法初始粒子在设计空间中的位置分布,在可能的优化区域,重点布置粒子,提高粒子种群针对特定优化问题的探索能力,提升粒子群算法的寻优精度。
(3)结合加强协同多学科优化理论,基于本文中所提方法,进行轿车车身侧面结构轻量化设计优化求解,实现结构最多减质量12.6kg,减质量效果达到14.6%,验证了本文中所提出方法在实际工程问题中应用的有效性,为实际车身多学科优化设计提供了可借鉴的方法和途径。
[1] KIANI M,GANDIKOTA I,RAIS-ROHANI M,et al.Design of lightweight magnesium car body structure under crash and vibration constraints[J].Journal of Magnesium&Alloys,2014,2(2):99-108.
[2] RYBERG A B,NILSSON L.A metamodel-based multidisciplinary design optimization process for automotive structures[J].Engineering with Computers,2015,31(4):711-728.
[3] BASTIEN C,PREM A,DICKISON M.Multidisciplinary design optimisation strategies for lightweight vehicle structures[C].LSDyna European Conference,2015.
[4] WANG P,GUANGQIANG W U.Multidisciplinary design optimization of vehicle instrument panel based on multi-objective genetic algorithm[J].Chinese Journal of Mechanical Engineering,2013,26(2):304-312.
[5] 王平,郑松林,吴光强.基于协同优化和多目标遗传算法的车身结构多学科优化设计[J].机械工程学报,2011,47(2):102-108.
[6] 史国宏,陈勇,杨雨泽,等.白车身多学科轻量化优化设计应用[J].机械工程学报,2012,48(8):110-114.
[7] 姜武华,王其东,何炜,等.基于可靠性的车桥结构多学科优化[J].汽车工程,2012,34(12):1136-1140.
[8] 史朝军,张胜兰,杨啓梁.自卸车货箱多学科优化设计[J].湖北汽车工业学院学报,2013,27(3):10-14.
[9] 李铁柱,李光耀,周泽,等.汽车转向盘骨架性能的多学科设计优化[J].汽车工程,2014,36(3):378-382.
[10] KENNEDY J,EBERHART R.Particle swarm optimization[C].IEEE International Conference on Neural Networks,1995.Proceedings,1995:1942-1948.
[11] BANBURY J.Experimental analysis of bound handling techniques in particle swarm optimization[J].IEEE Transactions on Evolutionary Computation,2013,17(2):259-271.
[12] YANG J M,CHEN Y P,HORNG J T,et al.Applying family competition to evolution strategies for constrained optimization[C].Evolutionary Programming Vi, International Conference,Ep97, Indianapolis, Indiana, Usa, April 13-16,1997, Proceedings.DBLP,1997:201-211.
[13] HOMAIFAR A,QI C X,LAI S H.Constrained optimization via genetic algorithms[J].Simulation Transactions of the Society for Modeling&Simulation International,2010,62(4):242-253.
[14] ROTH B,KROOI.Enhanced collaborative optimization:application to an analytic test problem and aircraft design[C].Aiaa/issmo Multidisciplinary Analysis and Optimization Conference,2006.
[15] LIU Z, LU J, ZHU P.Lightweight design of automotive composite bumper system using modified particle swarm optimizer[J].Composite Structures,2016,140:630-643.

