基于质量与坡度辨识的汽车自动变速器换挡控制研究∗

夏　光，涂波涛，唐希雯，陈无畏

前言

传统的两参数与三参数换挡策略，没有考虑汽车行驶工况，更不能针对驾驶员意图制定合理的换挡策略。坡道行驶时采用传统的换挡规律容易发生意外升降挡，在制定坡道换挡策略过程中，整车质量与道路坡度是必须考虑的因素[1]。

文献[2]中提出通过换挡离合器接合时的发动机转速，判断车辆是否处于坡道行驶工况，但未识别出坡度大小。文献[3]中通过传感器测量加速度，对比加速度区间的方法识别坡度，但未考虑整车质量的变化。文献[4]中采用了多种传感器信息融合的方法识别坡度，但该方法对传感器精度要求高，实验成本高。文献[5]中在SAEJ1939协议的基础上通过CAN得到了汽车发动机的输出转速和转矩，对转速进行差分获得了汽车行驶加速度和道路综合阻力，依据车辆纵向动力学原理进行道路坡度辨识，但当道路坡道变化较大时，辨识精度不高。文献[6]中采用多定遗忘因子最小二乘法辨识整车质量与道路坡度，对不同的待辨识参数赋予不同遗忘因子，虽然考虑了道路坡度的时变特征，但忽视了整车质量的变化，导致辨识参数准确性下降。文献[7]中通过对比递推最小二乘法与多定遗忘因子最小二乘法对整车质量与坡度的辨识结果，证明带定遗忘因子最小二乘法参数辨识效果优于递推最小二乘法辨识效果，但在选取遗忘因子时，同样忽略了整车质量的变化。文献[8]中指出车辆载荷对车辆控制性能的影响，采用多定遗忘因子最小二乘法和扩展卡尔曼滤波等方法辨识整车质量与坡道，但依然没有考虑车辆在行驶过程中整车质量的变化。文献[9]中采用定遗忘因子最小二乘法对重型车辆的质量和道路的坡度进行辨识，将整车质量辨识遗忘因子取1，同时忽视了重型车辆作业时整车质量的变化。文献[10]中通过构造车辆侧向动力学遗忘因子最小二乘递推模型和车辆纵向动力学遗忘因子最小二乘递推模型辨识整车质量，并在此基础上通过分析车辆纵向动力学特性，辨识道路坡度，增加了辨识工作量，实时性下降。文献[11]中在分析车辆纵向动力学模型基础上，采用卡尔曼滤波的方法辨识整车质量和道路坡度，虽然卡尔曼滤波具有良好的跟踪能力，但在辨识前须通过大量计算统计相关噪声，工作量大。

本文中提出了一种变遗忘因子最小二乘法进行整车质量和道路坡度辨识，可准确地辨识参数，较好地跟踪车辆纵向动力学系统动态变化特性；在完成参数辨识的基础上采用坡道换挡分层修正控制策略，将汽车坡道自动变速控制分为上层决策层与下层换挡执行层，其中，上层决策层采集汽车参数，辨识整车质量与坡度，综合决策并发出换挡修正控制指令；下层接收上层指令，执行换挡；最后进行了仿真与硬件在环实验，验证坡道换挡分层修正控制策略的正确性。

1　汽车行驶纵向动力学模型

汽车直线行驶时的总阻力为

式中:Ff为滚动阻力；Fw为空气阻力；Fi为坡度阻力；Fj为加速阻力。

其中空气阻力Fw为

式中:CD为空气阻力系数；A为汽车迎风面积；va为车速。

滚动阻力Ff和坡道阻力Fi为

式中:β为坡度角；f0为汽车的滚动阻力系数。

汽车滚动阻力系数采用两段滑行法测量[12]:测量汽车从高速va1滑行至vb1＝va1-5的滑行时间记为t1，汽车从低速va2滑行至vb2＝va2-5的滑行时间记为t2，由此可得

式中:vai为汽车滑行初速度；vbi为汽车滑行末速度；ai为两段滑行平均减速度；vi为滑行平均速度，i＝1，2。

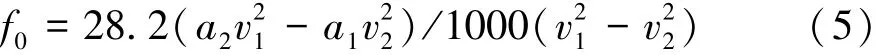
加速阻力为

式中:σ为旋转质量换算系数；a为汽车行驶加速度。

汽车行驶动力方程为

式中Ft为汽车驱动力。

驱动力Ft为

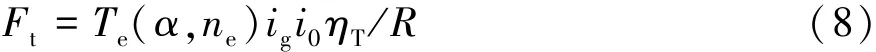
式中:Te为发动机的输出转矩；α为油门开度；ne为发动机转速；ig为变速器传动比；i0为主减速器传动比；ηT为传动系统效率；R为轮胎有效滚动半径。

2　整车系统动力学模型的建立

2.1　发动机模型

发动机工作时不可能时刻处于稳态工况。大量研究表明，发动机在非稳态工况下，其工作特性与其稳态特性存在较大差异，因此须对发动机稳态工况下的输出转矩进行修正。目前，常用的发动机稳态特性的修正方法是系数修正法，修正后的非稳态工况发动机输出转矩为

式中:λ为非稳态工况下发动机输出转矩下降系数，取值范围为0.07～0.09，与发动机有关；we为发动机输出曲轴角速度。

2.2　整车模型

整车模型由发动机模型、变速器模型、换挡规律模型、换挡规律逻辑判断模型和汽车动力学模型等组成。

3　基本换挡规律

求解换挡点主要有作图法和解析法两种。作图法工作量大，作图过程误差大，很难得到精确的换挡点；解析法可通过MATLAB编写程序，由计算机计算，只须输入基本参数和相应的计算公式，便可获取准确的换挡点，本文中采用解析法求解动力性换挡规律和经济性换挡规律。

3.1　动力性换挡规律

动力性换挡规律是指汽车在换挡前后始终可获得最大加速度(或最大驱动力)的换挡规律。动力性换挡规律是由动力性升挡规律和动力性降挡规律共同组成，其中动力性降挡规律是基于动力性升挡规律获得的。动力性换挡曲线如图1所示，实线表示动力性升挡曲线，虚线表示动力性降挡曲线。

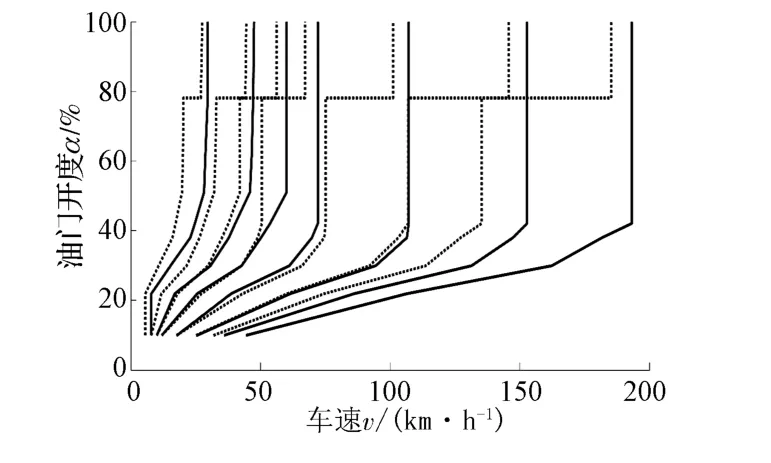
图1　动力性换挡曲线

3.2　经济性换挡规律

经济性换挡规律主要目标是汽车换挡前后燃油消耗量始终处于最低水平。经济性换挡规律由经济性升挡规律和经济性降挡规律共同组成，其中经济性降挡规律是基于经济性升挡规律获得的。经济性换挡曲线如图2所示，实线表示经济性升挡曲线，虚线表示经济性降挡曲线。

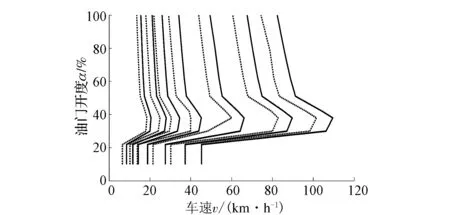
图2　经济性换挡曲线

4　基于变遗忘因子最小二乘算法的质量与坡度辨识

4.1　基本最小二乘法

最小二乘法为系统辨识问题提供较好的解决方法，相比于其他算法，最小二乘法实施简单，不仅可以应用于静态系统，也可应用于动态系统。其基本原理如下[13]。

对于SISO系统描述为

式中:y(k)为系统输出；u(k)为系统输入。

对于上式描述的系统有两个问题需要解决:其一是系统的阶次na，nb的确定；其二是系统参数的辨识，即求出系统描述方程。

考虑到测量误差和模型误差和干扰的存在，将实际采集到的输入和输出数据代入式(10)，同样存在一定误差，用e(k)表示该误差，则式(10)变为

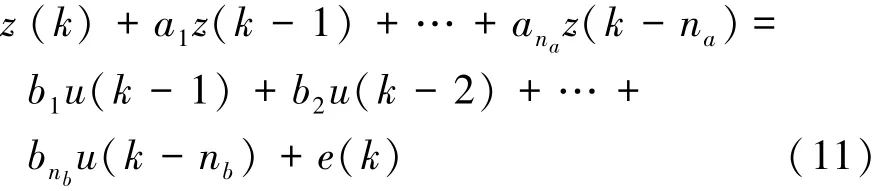
将式(11)改写为

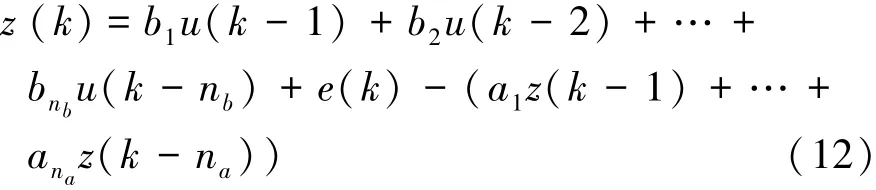
由上式可得系统的输入输出最小二乘格式为

其中:

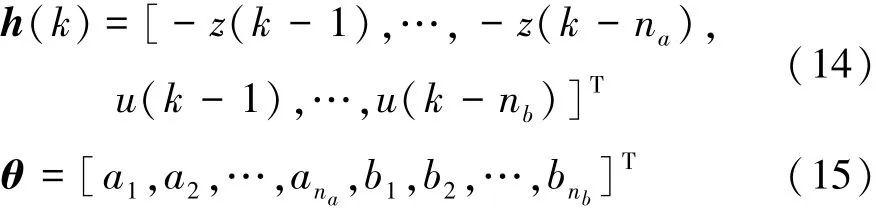
式中:h(k)为样本集合；θ为待辨识参数集合。

取准则函数:

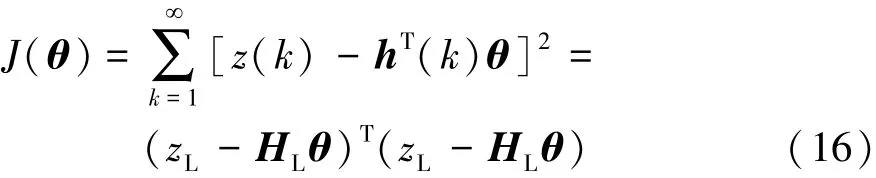
极小化J(θ)，求得参数θ的估计值，将使模型的输出最好地预报系统的输出。即令:

4.2　变遗忘因子最小二乘法

时变系统的动态特性通常不是稳定变化的，利用基本最小二乘法进行参数辨识时，数据容易饱和，算法就会慢慢失去修正能力，辨识误差较大，甚至无法更新[14]。定遗忘因子的最小二乘法适应系统时变特征能力较弱。如果算法的遗忘因子可随着系统动态特性的变化而自适应变化，辨识算法就能更好地跟踪系统的动态变化[15]。

变遗忘因子法的递推算法为

式中:l为遗忘步长；M为设计参数，可以是常数，也可是变量，但须满足0＜fk＜1；e(k＋1)为系统k＋1时刻的有色噪声；fk＋1为k＋1时刻系统的遗忘因子；Qk＋1为系统k＋1时刻的增益；θ(k＋1)为系统k＋1时刻的参数估计值；Pk＋1为系统k＋1时刻数据协方差矩阵。

4.3　坡度与整车质量辨识

采用定遗忘因子最小二乘法辨识坡度与整车质量时，通常默认整车质量几乎不变，而汽车在行驶过程中，整车质量可能随时发生变化，典型的是工程车、城市公交车，若采用定遗忘因子最小二乘算法辨识整车质量就存在缺陷。另一方面由于遗忘因子固定，导致定遗忘因子最小二乘法参数辨识动态特性不好。由于变遗忘因子最小二乘法能跟随汽车行驶动力学系统特性变化，能实时辨识整车质量，同样也能保证坡度识别的准确性。

由汽车行驶纵向动力学方程，将式(1)～式(3)和式(6)～式(8)整理成

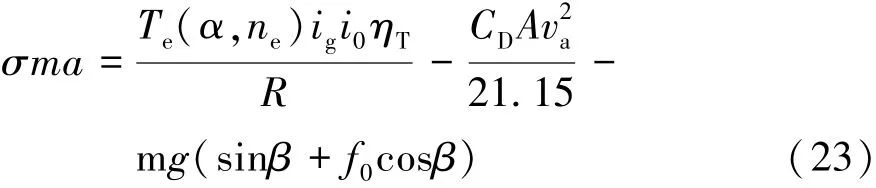
将式(23)整理成

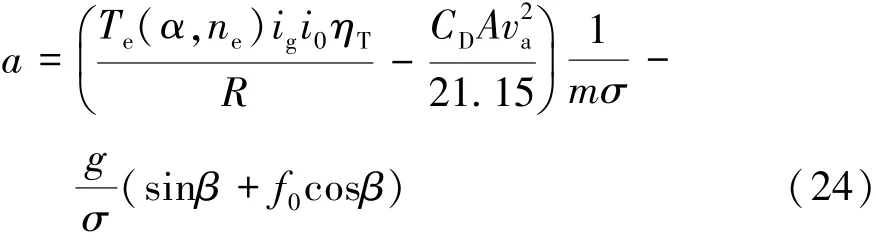
将式(24)整理得

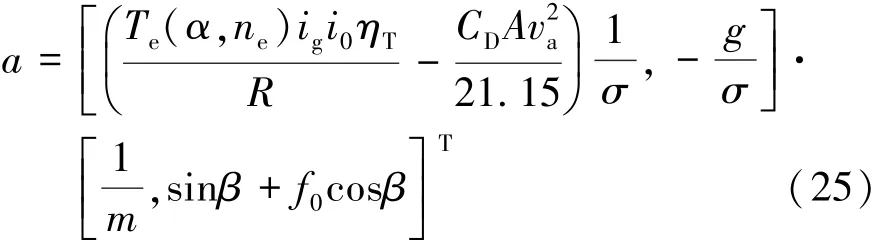
由式(13)最小二乘格式，将式(25)整理成最小二乘格式:

上述公式中z(k)为汽车行驶动力学系统中输出，实际为汽车加速度，可通过汽车加速度传感器获得。

由式(25)～式(27)得

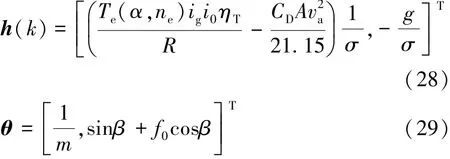
式中:h(k)为汽车行驶动力学系统中样本集合；θ为待辨识参数。

4.4　辨识流程

在辨识过程中，h(k)为系统辨识数据样本，可通过实车采集。θ为待辨识参数向量，在进行辨识时，设初始辨识值足够小，θ＝(0.001，0.001)；设协方差矩阵P(0)＝106×I；设初始遗忘因子为0.99。

基于汽车纵向动力学方程，基于变遗忘因子最小二乘法的参数辨识程序流程如图3所示。

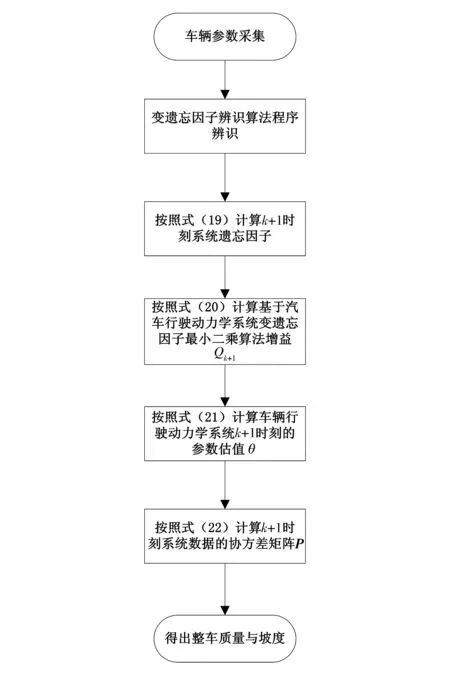
图3　基于变遗忘因子最小二乘法的参数辨识流程图

4.5　坡度映射仿真

通过变遗忘因子辨识出的目标函数为

式中f0由式(5)算出。

运用Matlab神经网络工作箱，建立BP神经网络。f(β)到β为同胚映射[16]，网络的输入为f(β)，网络输出为tanβ，通过生成的BP网络Simulink模块，对辨识出的坡度仿真，取仿真时间100s，辨识出的坡度与真实坡度对比如图4所示，可以看出采用变遗忘因子二乘法能很好地辨识坡道坡度。

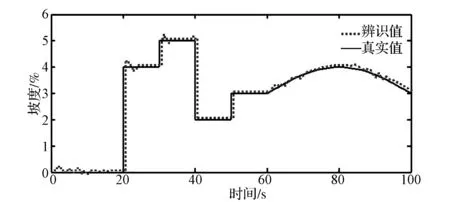
图4　坡度辨识值与真实值

4.6　整车质量的辨识

当汽车整备质量为 1 470kg，整车质量为1 750kg，汽车行驶50s时，由于乘员下车整车质量变为1 540kg，通过变遗忘因子最小二乘法辨识出整车质量，与真实值对比如图5所示，可以看出对于变质量有着较高的辨识精度。

图5　整车质量辨识对比图

5　坡道换挡策略与仿真

5.1　坡道工况换挡分层修正控制策略

当辨识出汽车在水平路面行驶时，汽车自动变速按照正常换挡规律换挡，不进行换挡修正和干预。

当辨识出汽车处于坡道工况时，换挡采用坡道换挡分层修正控制策略[17]，上层决策层通过变遗忘因子最小二乘法辨识整车质量和坡度，并对整车质量与坡度按照专家经验进行等级划分:设定汽车空载质量为mK，满载质量为mM，则小质量的范围为[mK，mK＋0.2(mM-mK))，中质量的范围为[mK＋0.2(mM-mK)，mK＋ 0.8(mM-mK))，大质量的范围为[mK＋ 0.8(mM-mK)，mM]。

通常情况下，在城市和良好公路上行驶的轿车，最大爬坡度为17.6%，载货汽车的最大爬坡度为30%，越野车的最大爬坡度应大于57.7%。再根据我国现行的JTG D20—2006《公路路线设计规范》条例，公路的纵向坡度最大值不可超过8.9%，特殊情况可增加，但最高不得超过11.92%，根据上述汽车的最大爬坡度范围、现行公路的最大坡度范围和城市地下车库出入坡道实际情况，选择17.6%为坡道纵向坡度的最大值，设定小坡坡度绝对值范围[1%，3%)，中坡坡度绝对值范围[3%，10%]，大坡坡度绝对值范围(10%，17.6%]。坡道工况换挡分层修正控制策略流程如图6所示。

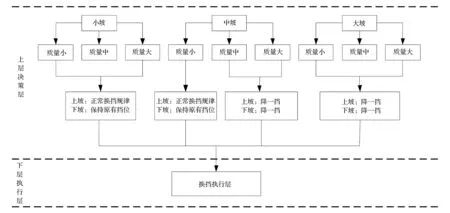
图6　坡道工况换挡分层修正控制流程

5.1.1上坡工况换挡分层修正控制策略

汽车处于上坡工况时，采用上坡换挡分层修正控制策略。上层决策层通过变遗忘因子最小二乘法辨识整车质量和坡度，并对整车质量与坡度进行等级划分与综合决策，得到不同整车质量与坡度的换挡修正控制策略；例如，当辨识出汽车行驶在小坡且车辆为小质量时，则挡位修正控制决策为变速器按照正常换挡规律换挡；当辨识出汽车行驶在中坡且车辆为中质量时，则挡位修正控制决策为汽车按照坡道行驶换挡控制策略换挡，在上坡前挡位基础上下降一挡同时禁止升挡。

5.1.2下坡工况换挡分层修正控制策略

下坡时驾驶员多采用制动器制动以降低车速，导致制动摩擦片温升过高而制动效能下降，特别是下长坡时，情况更为严重，容易发生交通事故。因此下坡时汽车应以低挡行驶且限制升挡，充分利用发动机的拖动转矩进行辅助制动。汽车处于下坡工况时，采用下坡换挡分层修正控制策略。上层决策层通过变遗忘因子最小二乘法辨识整车质量和坡度，并对整车质量与坡度进行等级划分与综合决策，得到不同整车质量与坡度的换挡修正控制策略，即:在原有挡位基础上下降若干个挡位且禁止升挡。

5.2　坡道换挡控制策略的仿真分析

基于Matlab/Simulink搭建整车模型，分别采用基于坡度与整车质量辨识的“换挡分层修正控制策略”与未采用换挡修正控制的传统换挡控制策略进行仿真，仿真工况为在匀速上坡工况与下长坡工况，整车参数如表1所示。

5.2.1匀速上坡工况

汽车以40km/h的速度、挡位为6挡、整车质量为1 600kg，匀速上10%坡度的坡道，分别对汽车换挡分层修正控制策略与传统换挡控制策略在特定工况下进行仿真，挡位变化曲线如图7所示。

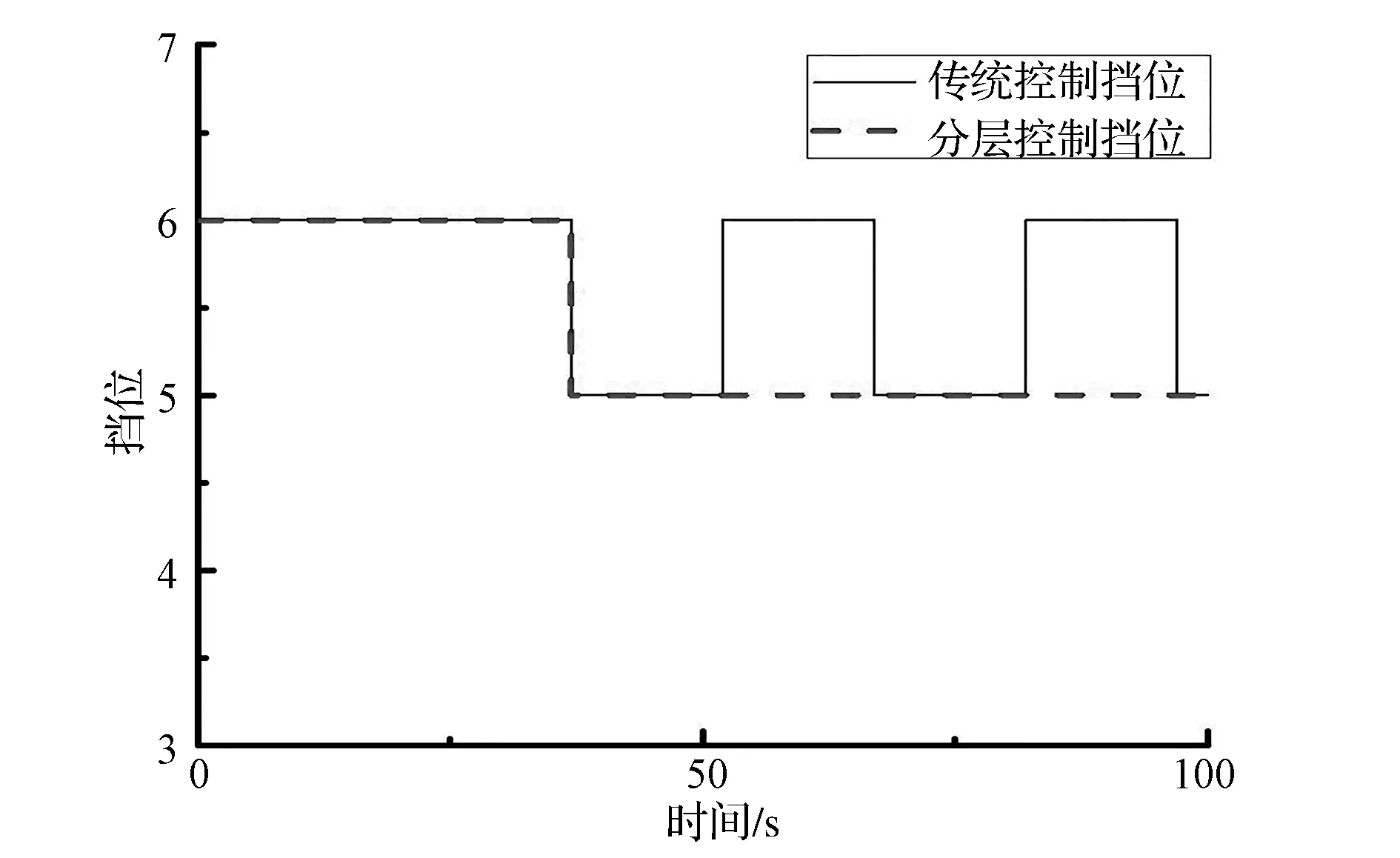
图7　匀速上坡挡位信号图

由图7可知，采用传统换挡控制策略时，汽车在6挡爬坡过程中，由于行驶阻力增加使汽车减速，此时驾驶员为了保持汽车匀速上坡，必须加大油门开度，达到5挡的降挡条件，则降为5挡，驱动力大于行驶阻力，车速上升；为保持汽车匀速上坡，驾驶员减小油门开度，以达到6挡的升挡条件，则升入6挡，驱动力不足，需要加大油门开度，则再次达到5挡的降挡条件，降为5挡，此类频繁的升降挡一直重复至上坡工况结束，加剧了传动系统部件的磨损，同时汽车平顺性变差；采用坡道换挡分层修正控制策略时，汽车爬坡过程中，通过综合辨识出整车质量与坡度，换挡修正控制策略为降一挡且限制升挡，换挡循环现象消除，行驶平顺得到改善。

5.2.2下长坡工况

汽车以60km/h的速度、挡位为6挡、整车质量为1 600kg，下8%坡度的大长坡道，分别对汽车换挡分层修正控制策略与传统换挡控制策略在特定工况下进行仿真，挡位变化曲线如图8所示。

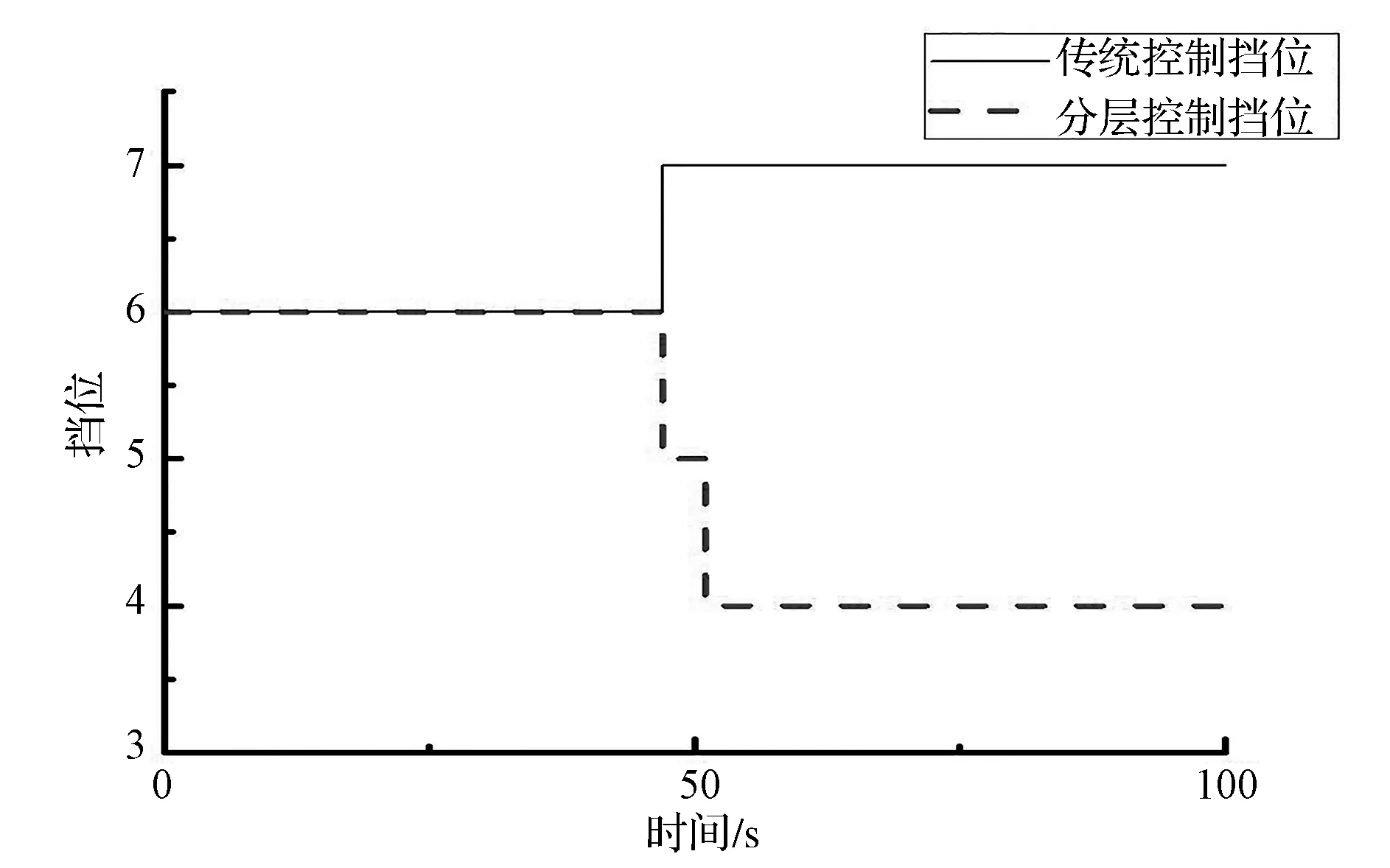
图8　下长坡挡位信号图

由图8可知，采用传统换挡控制策略，汽车在6挡下坡过程中，驾驶员为了控制车速，油门开度为零；但随着下坡过程中车速增加，达到7挡的升挡条件，驾驶员需要通过制动器制动以降低车速，则加剧了制动器的磨损，使得长下坡工况下制动器温度升高，引起制动器热衰退而影响制动性能；采用坡道换挡分层修正控制策略时，在下小坡时通过限制变速器升挡，在下大坡时，将变速器下降两个挡位且限制升挡，以充分利用发动机的拖转制动，同时减少制动器的磨损，降低制动器的温度。

由以上仿真结果可知:采用传统换挡控制策略坡道行驶，匀速上坡时频繁升降挡，下长坡时升入高挡需要制动系统辅助减速；采用坡道换挡分层修正控制策略时，匀速上坡时能适时降挡且抑制升挡，消除换挡循环现象，在下坡时能消除不当升挡现象并适时降挡，充分利用发动机拖动转矩减速，平稳下坡。

6　硬件在环实验

6.1　硬件在环实验台的搭建

通过建立自动变速器硬件在环实验台以模拟实车行驶状态，获取行驶状态参数，并基于Labview设计上位机控制软件，进行硬件在环实验。硬件在环实验台设计包括实验台架的总体结构组装、线路布置和电机调试和实验台上位机控制软件设计。

基于设计的自动变速器硬件在环实验台，依据上述坡道换挡分层修正控制策略，通过Labview模拟坡道行驶参数，输入模块通过采集传感器信号，并经过处理器处理，处理器包含变遗忘因子最小二乘算法程序、自动变速挡位分层修正控制策略。处理器发出坡道工况挡位修正控制信号，由功率放大器放大，再由实验台换挡执行机构进行换挡。实验台实物图如图9所示。

图9　硬件在环实验台实物图

6.2　硬件在环实验方案与结果分析

通过对实验样车以不同的油门开度上不同坡度的工况采集实车行驶速度和加速度参数，输入到Labview中，模拟不同的车速加速度，通过处理器的辨识算法程序，辨识出整车质量和坡度并采用坡道换挡分层修正控制策略，最后由硬件在环实验台换挡执行电机执行换挡，硬件在环实验方案如图10所示。

硬件在环实验台模拟的路面坡度如图11所示。

图10　硬件在环实验方案

图11　硬件在环路面坡度示意图

采用传统换挡控制策略与坡道换挡分层修正控制策略仿真，挡位信号如图12所示。

图12　硬件在环实验挡位变化图

由图12可知:采用传统换挡控制策略时，汽车以5挡在水平路面行驶，在第24s后进入上坡工况，则挡位一直在4挡与5挡间变换，这种频繁的升降挡持续到上坡工况结束为止；汽车在第70s进入下坡工况，油门开度为零，因达到升挡条件而升挡。采用坡道换挡分层修正控制策略时，汽车处于匀速上坡工况时的频繁升降挡现象消除，下坡工况以低挡下坡。

硬件在环实验结果表明:变遗忘因子最小二乘法可准确地辨识整车质量与坡度；基于坡度与质量辨识的坡道换挡分层修正控制策略，在匀速上坡时消除了频繁换挡现象；在下坡时避免了意外升挡且适时降挡，充分利用发动机制动，改善了制动器的磨损现象。

7　结论

(1)基于变遗忘因子最小二乘法的整车质量与坡度辨识方法，能较好地跟踪系统的动态变化特性，准确辨识整车质量与坡度。

(2)基于坡度与质量辨识的汽车坡道换挡分层修正控制策略，将汽车自动变速器控制分为上层决策层与下层换挡修正执行层，能根据不同坡道工况进行挡位控制，提高了汽车自动变速的智能化水平。

(3)采用基于整车质量与坡度辨识的汽车换挡分层修正控制策略，在上坡时可有效地避免换挡循环，减少换挡执行部件磨损，提高汽车的行驶平顺性与换挡部件的寿命；在下长坡时通过限制挡位升高，充分利用发动机的拖转制动，减少制动系统部件的磨损，提高制动系统的使用寿命和汽车行驶安全性。

[1] 张勇，许纯新.车辆质量参数对最佳换挡点的影响[J].农业机械学报，2002，33(2):8-10.

[2] 何忠波，白鸿柏，张培林，等.AMT车辆坡道换挡策略与试验研究[J].农业机械学报，2007，38(2):13-16.

[3] 金辉，李磊，李斌虎，等.基于加速度区间判断的坡道识别方法[J].中国公路学报，2010，23(1):122-126.

[4] 杨志刚，曹长修，苏玉刚.动态识别道路坡度的多传感器信息融合方法[J].重庆交通大学学报，2002，21(2):97-102.

[5] 王玉海，董瑞先，王松，等.基于 SAE J1939协议的重型车辆坡道识别实时算法[J].汽车工程，2010，32(7):640-642，647.

[6] 赵治国，王琪，刁威振，等.双离合器变速汽车坡道模糊修正换挡研究[J].中国机械工程，2013，24(15):2122-2129.

[7] VAHIDIA，DRUZHININA M，STEFANOPOULOU A，et al.Simultaneous mass and time-varying grade estimation for heavy-duty vehicles[C].American Control Conference，Proceedings of the 2003.IEEE，2003，6:4951-4956.

[8] KIDAMBI N，HARNE R L，FUJII Y，et al.Methods in vehicle mass and road grade estimation[J].SAE International Journal of Passenger Cars-Mechanical Systems， 2014， 7(3):981-991.

[9] VAHIDI A， STEFANOPOULOU A， PENG H.Recursive least squares with forgetting for online estimation of vehicle mass and road grade:theory and experiments[J].Vehicle System Dynamics，2005，43(1):31-55.

[10] KIM I， KIM H， BANG J， et al.Development of estimation algorithms for vehicle’s mass and road grade[J].International Journal of Automotive Technology， 2013， 14(6):889-895.

[11] MAHYUDDIN M N，NA J，HERRMANN G，et al.Adaptive observer-based parameter estimation with application to road gradient and vehicle mass estimation[J].IEEE Transactions on Industrial Electronics， 2014， 61(6):2851-2863.

[12] 董金松，许洪国，任有，等.基于道路试验的汽车滚动阻力和空气阻力系数计算方法研究[J].交通信息与安全，2009，27(1):75-78.

[13] 候媛彬，侯梅，等.系统辨识及其MATLAB仿真[M].北京:科学出版社，2004:53-88.

[14] 庞中华，崔红.系统辨识与自适应控制MATLAB仿真[M].北京:北京航空航天大学出版社，2009:27-38.

[15] 刘党，蔡远文，苏永芝.系统辨识方法及应用[M].北京:国防工业出版社，2010:110-141.

[16] 李大华.应用泛函简明教程[M].武汉:华中理工大学出版社，1999:57-87.

[17] 夏光，唐希雯，孙保群，等.汽车自动变速分层协调换挡控制[J].交通运输工程学报，2012，12(4):50-58.