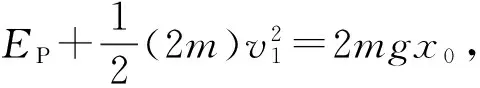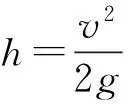弹簧问题解答脉络
(浙江省宁波市鄞州区教育局教研室,浙江 宁波 315100)
弹簧问题涉及高中物理力、运动、能、动量等重点知识,其问题解决要应用对称、等效、图像等方法,是训练学生综合运用物理知识与方法的重要题材,也是高考命题的热点。在物理高考复习中,笔者建议开设专题复习,帮助学生理顺弹簧问题解答脉络,提高解决问题的能力。本文就此介绍弹簧问题的解题脉络,期待能抛砖引玉。
1 关于轻弹簧的四个基本认识
1.1 轻弹簧上弹力处处相同,弹力与形变量满足的关系是F=kΔx
由胡克定律可以知道,在弹性限度内,轻弹簧的弹力F和轻弹簧的形变量Δx成正比,即F=kΔx,其中k是轻弹簧的劲度系数。
例1:如图1所示,两根劲度系数分别为k1和k2的轻弹簧竖直悬挂,弹簧下端用光滑轻绳连接,并有一光滑滑轮放在该绳上,当滑轮下挂一重G的物体后,滑轮下降的距离为()。

1.2 弹力随形变量变化而变化,需要经历过程而非突变
由于弹簧的弹力与其形变量有关,而形变量的变化是需要时间的,因此,弹簧的弹力变化也需要时间,即弹力的变化需要经历一个过程而不能突变。
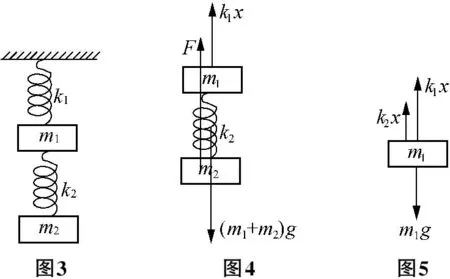
例2:如图3所示,劲度系数分别为k1、k2的轻弹簧竖直悬挂,两弹簧间连一质量m1的重物,最下端挂一质量为m2的重物,用力竖直托起m2,当此力为多大时两弹簧总长等于两弹簧原长之和?撤去此力瞬时两重物加速度大小与方向如何?
解析:若k1弹簧压缩,那么k2弹簧必拉伸,则m1无法平衡。故k1弹簧拉伸,k2弹簧压缩,且两弹簧形变量相同。
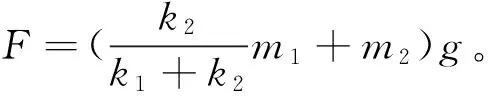
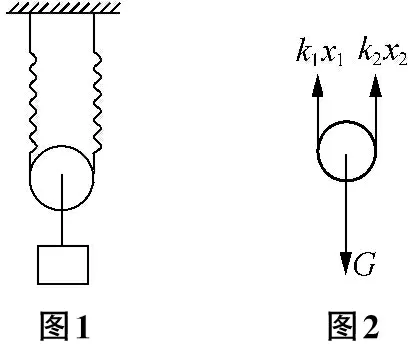
1.3 等效弹簧的劲度系数

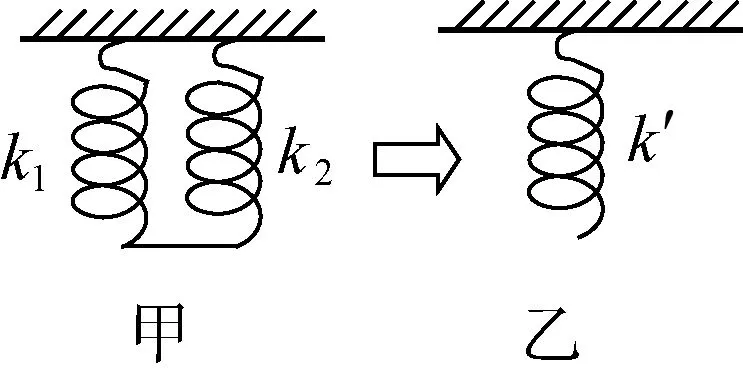
图6
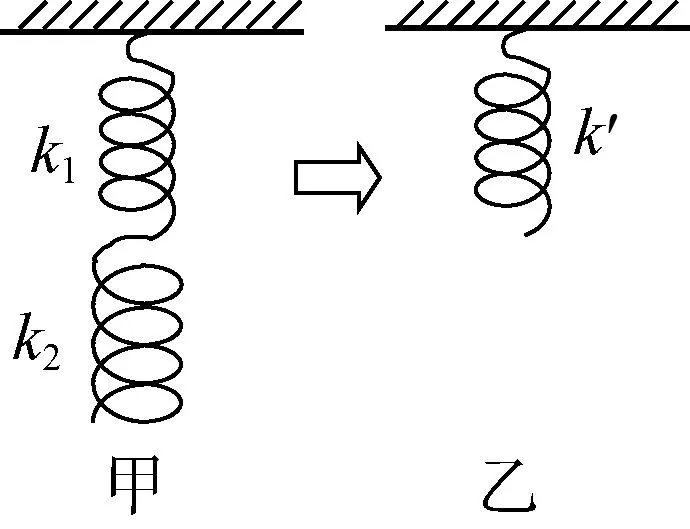
图7
例3:如图8甲所示,一根轻弹簧竖直放在桌面上,上端放一重物m,稳定后弹簧长为L,现将弹簧截成等长的两段,将重物等分成两块,如图乙所示连接后稳定时两段弹簧的总长为L′,则()。
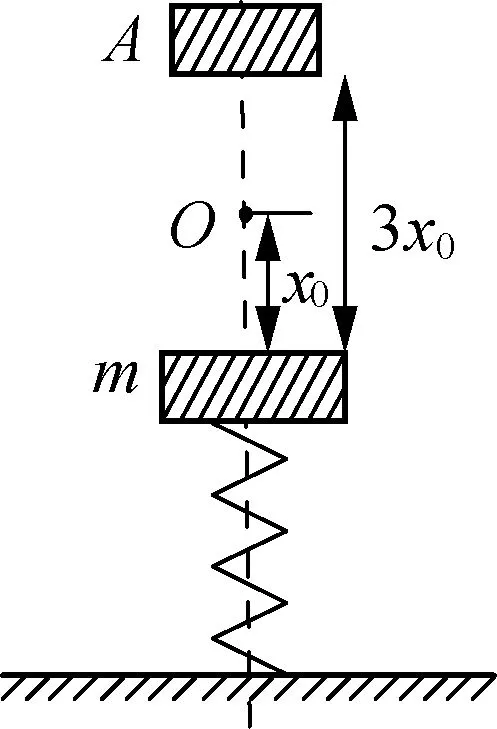
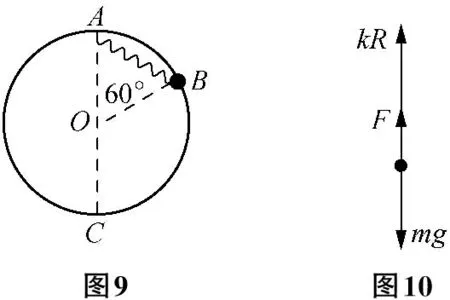
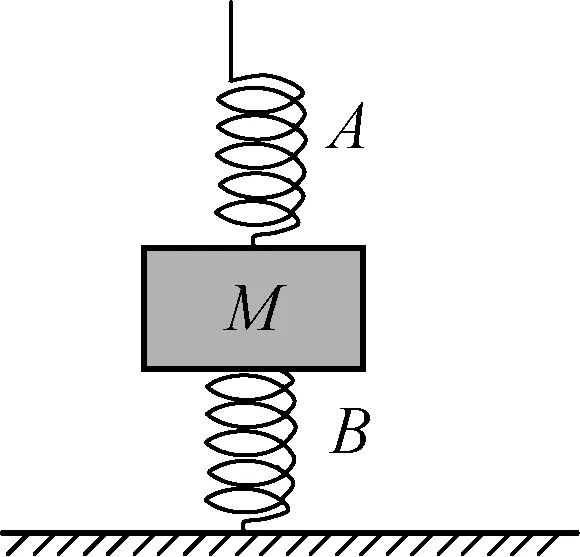
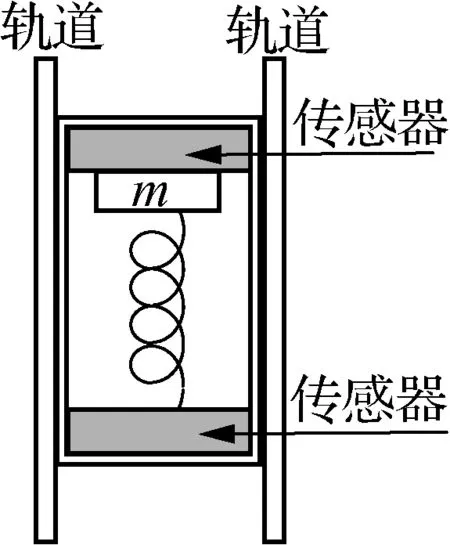
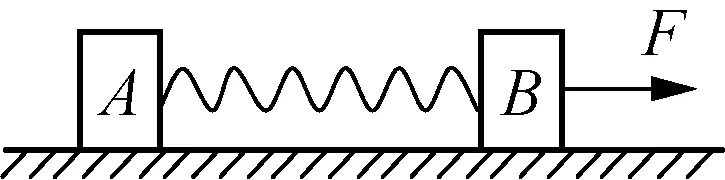
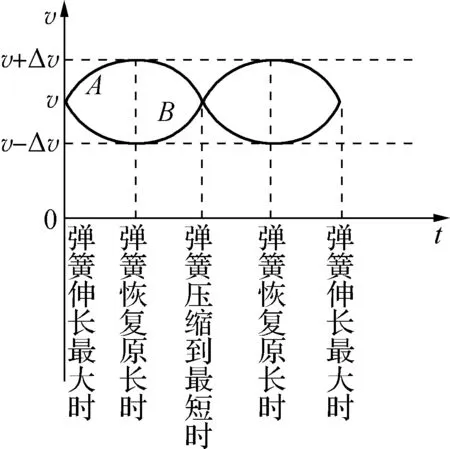
A.L>L′B.L C.L=L′D. 无法确定 图8 例4:一个质量为m=0.2kg的小球系于轻弹簧的一端,且套在光滑竖直的圆环上,弹簧固定于环的最高点A,环的半径R=0.50m,弹簧原长L0=0.50m,劲度系数为4.8N/m,如图9所示,若小球从图示B点由静止开始滑到最低点C时,弹簧的弹性势能E弹=0.60J,g取10m/s2,求: (1) 小球到C点时的速度vc的大小; (2) 小球在C点时对环的作用力。 由胡克定律可知,弹簧的形变具有对称性,当伸长量与压缩量相同时,弹簧产生的弹力大小相等。 图11 例5:如图11所示,物体质量为M,与弹簧A、B相连接,弹簧下端固定于地,弹簧A、B质量均不计,劲度系数分别为k1、k2,试求用手拉住弹簧A的上端,缓慢上移多大距离能使弹簧B产生的弹力为原来的2/3? “整”是将多个个体或多个局部视为整体的一种分析问题的方法,从较大的视野去观察、分析和解决问题;“分”是以一个个体或局部为研究对象的一种分析问题的方法。针对不同的问题和研究对象,可以先整后分、先分后整,或整、分同步进行。 例6:如图12所示,将金属块m用压缩的弹簧卡在一个矩形的箱子中,在箱的顶板和底板装有压力传感器,可以显示出压力的大小,箱可以沿竖直轨道运动。当箱子以a=2.0m/s2的加速度竖直向上做匀减速运动时,顶板的传感器显示的压力为6.0N,底板传感器显示的压力为10.0N,g取10m/s2。 图12 (1) 当顶板传感器的示数是底板传感器的示数的一半时,试判断箱子的运动情况; (2) 要使顶板传感器的示数为零,箱子沿竖直方向的运动情况可能是怎样的? 解析:(1) 当箱子向上减速运动时,底板压力传感器读数为10.0N,即弹簧上弹力为10.0N,弹簧处于压缩状态,对于金属块,由牛顿第二定律,有:mg+F上-F弹=ma,得m=0.5kg。 速度图像能反映物体在各个时刻速度和加速度的大小、方向及其变化趋势,从而也可以判断物体运动的动能、动量等物理量的变化趋势。 例7:如图13所示,光滑水平面上有质量相等的两个滑块,它们之间用一轻弹簧相连接。现用一水平力F向右拉滑块B,经过一段时间后系统做匀加速运动。若某时刻去掉水平力F,则以后的运动情况是()。 图13 A. 任一时刻两滑块加速度大小相等 B. 当弹簧伸长量最大时,两滑块动量相等 C. 当弹簧恢复原长时,两滑块速度必相同 D. 当弹簧压缩到最短时,两滑块的动量均为零 解析:去掉水平力F后,A、B两滑块以相同的初速度分别做不同的运动: (1)A先做加速度减小的加速运动,B做加速度减小的减速运动,弹簧伸长量减小,弹簧长度减小; (2) 当弹簧恢复原长时,A的速度最大,B的速度最小; (3) 接着A做加速度增大的减速运动,B做加速度增大的加速运动,弹簧压缩量增大,弹簧长度继续减小; (4) 当弹簧长度最短时,A、B的速度相同; (5) 此后,A做加速度减小的减速运动,B做加速度减小的加速运动,弹簧的压缩量减小,弹簧长度增大; (6) 当弹簧恢复原长时,A的速度最小,B的速度最大; (7) 接着,A做加速度增大的加速运动,B做加速度增大的减速运动,弹簧的伸长量增大,弹簧长度增大; (8) 当弹簧长度最长时,A、B的速度相同,A、B运动情形回到力F刚撤去时的运动状态,当然系统已经向原运动方向平移了一段距离。 上述关于A、B运动的分析,我们也可以用v-t图像来定性表示,如图14所示。本题的答案是A、B。 图14 做功伴随着能的变化,弹力做功时弹性势能变化,弹力做功的多少与弹性势能变化量在数值上是相等的。弹簧的压缩量与伸长量相等时,弹性势能的变化量在数值上也是相等的。 图15 例8:质量为m的钢板与直立轻弹簧的上端连接,弹簧下端固定在地面上,平衡时,弹簧的压缩量为x0,如图15所示,一物块从钢板正上方距离3x0的A处自由落下,打在钢板上并立刻与钢板一起向下运动,但不粘连,它们到达最低点后又向上运动。已知物块质量也是m时,它们恰好回到O点;若物块质量为2m,仍从A处自由落下,则物块与钢板回到O点时,还具有向上的速度,求物块向上运动到达的最高点与O点距离。 参考文献: [1]张加强,张安诚.谈高考弹簧一类问题难点突破.[J].物理之友,2001,(4). [2]张善贤.连结弹簧振子的能量转化和动量传递[J].物理之友,2001,(2). [3]张政宗.一组与弹簧相关运动的临界问题[J].物理之友,2001,(2). [4]王路宝.例谈无外力作用下的水平弹簧双振子模型[J].物理之友,2017,(2). [5]王彬.一道涉及轻弹簧习题引发的思考[J].物理之友,2014,(9).
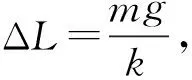
1.4 弹簧弹力为保守力


2 分析弹簧问题的四个思路
2.1 熟用胡克定律,注意形变性质

2.2 善用整、分结合法简化过程


2.3 巧用速度图像展示系统各部分的运动状态
2.4 利用功能关系确定弹性势能