NIC-平面图中的轻边存在性及其定向染色

刘维婵

LIU Weichan

西安电子科技大学 数学与统计学院，西安 710071

School of Mathematics and Statistics,Xidian University,Xi’an 710071,China

1　引言

图论是一门古老的数学分支，它起源于1736年欧拉对于哥尼斯堡七桥问题的研究。近年来，图论学科的发展非常迅速且应用广泛，已渗透到诸如语言学、物理学、化学、电讯工程、计算机科学以及数学的其他分支中，特别在计算机科学中，图论在如形式语言、数据结构、分布式系统、操作系统等方面均扮演着重要的角色。

本文研究图的拓扑结构，只考虑简单图。如果一个图可以画（嵌入）在平面上，使得不同的边互不交叉，则称这样的图是平面图，否则称为非平面图。一个平面图在平面上的嵌入称为平图。对于平图G，用V(G)、E(G)、F(G)分别表示它的点集合、边集合、面集合。著名的欧拉公式表明：

设G为一个图在平面上的嵌入，如果图G上存在交叉，则必然是G的某两条边交叉产生的，于是G中的每个交叉c都可以与G中的4个顶点（即两条交叉边上的4个顶点）所构成的点集建立对应关系，称这个对应关系为θ。如果对于G中任何两个不同的交叉（如果存在的话）c1与c2，有|θ(c1)⋂θ(c2)|≤1，则称图 G 是NIC-平面图。NIC-平面图的概念是由Zhang[1]于2014年提出的。容易看出，每个平面图都是NIC-平面图。

设℘是一个图类，如果对于℘中的任何一个图G，都存在一条边uv以及一个与图G的选择无关的常数ω，使得d(u)+d(v)≤ω，则称图类℘含有轻边。Kotzig[2]证明了每个3-连通的平面图都含有一条边uv，其两个顶点的度和至多为13。Fabrici与Madaras[3]证明了每个3-连通的1-平面图都含有一条边uv，其两个顶点的度都不会超过20。具有最小度限制条件的1-平面图的轻边或其他轻子图的存在性的研究可参见文献[4-12]。

下文中，对于NIC-平面图G，用δ(G)表示它的最小度，即度数（点所关联的边的条数）最小的顶点的度数；用g(G)表示它的围长，即图G所包含的所有圈中长度（圈所关联的边的条数）最短的圈的长度；用GX表示图G的关联平面图，即将图G的所有交叉全部看成是一个新的度数为4的点所得到的平图，这些新的点称为图GX的假点，其余的点称为图GX的真点；在图GX中关联假点的面称为假面，其余的面称为真面；k-点（面）或k+-点（面）指的是度数为k或至少为k的点（面）。其余未明确指出的定义或者记号可参阅文献[7]。

设G是一个围长至少为5的NIC-平面图。现从图G的每一对交叉边中去除一条，得到图H。容易看出，图H是一个围长至少为5的平面图。根据欧拉公式（1），可以得到[13]：

另一方面，Zhang[1]于2014年证明了图G的交叉数至多为3(|V(G)|-2)/5，因此：

从而图G的平均度为2|E(G)|/|V(G)|＜5，由此可得δ(G)≤4，即每个围长至少为5的NIC-平面图都含有一个度数不超过4的点。基于此，本文将研究围长至少为5且最小度为4的NIC-平面图的轻边存在性，并探讨其在定向染色中的应用。

2　NIC-平面图的轻边存在性

定理1设G是NIC-平面图，如果δ(G)=4且g(G)≥5，则G存在边uv，其中d(u)=d(v)=4。

证明 假设该命题的结论不成立，即对于G的任何一条边uv，当d(u)=4时，有d(v)≥5。

考虑图G的关联平面图GX，由于它是平面图，故根据欧拉公式（1），有：

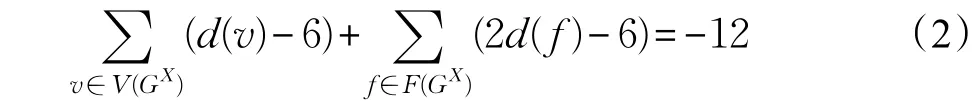
对于图GX的每个点v，定义权值c(v)=d(v)-6，对于每个面 f，定义权值c(f)=2d(f)-6。从而由式（2）可知：

接下来，定义权转移规则如下：

（R1）每个4-面向其关联的假4-点转移1/2。

（R2）设 f=uvwx为4-面且 x为假4点，如果v是真4-点，则 f向v转移5/6；如果u或w是真4-点，则 f向u或w转移1/2。

（R3）每个4+-面向其关联的5-点转移1/3。

（R4）设 f是一个5+-面，v是其关联的真4-点，如果v在 f的两个相邻点都是假4-点，则 f向v转移7/6；否则，f向v转移1。

（R5）每个5+-面向其关联的假4-点转移3/4。

设c*(v)与c*(f)为图GX中的点v与面 f在执行完上述权转移规则后的最终权值。

情况1点v是假4-点

如果点v关联4个4+-面，则由（R1）与（R5）可知：

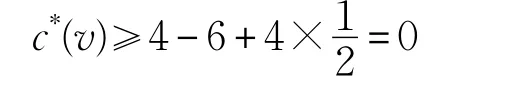
如果点v关联3-面，则由于图G是NIC的，并且其围长至少为5，推得点v关联2个5+-面与1个4+-面，从而根据（R1）与（R5）可知：

情况2点v是真4-点

记v1,v2,v3,v4为点v在GX中的4个邻点，并且f1,f2,f3,f4分别为与{vv1,vv2},{vv2,vv3},{vv3,vv4},{vv4,vv1}关联的面。

如果v在GX中的邻点都是真点，那么由图G的围长至少为5可得点v关联4个4+-面，从而根据（R2）与（R4）得到：

如果v在GX中的邻点有假点，则：

（1）当v在GX中的邻点中有且仅有1个假点时，若点 v关联4个4+-面时，由（R2）与（R4）得式（4）。若点v关联1个3-面时，则其关联3个4+-面，且其中1个是5+-面（否则与围长限制条件矛盾），因此根据（R2）与（R4），可得：

（2）当v在GX中的邻点中有且仅有2个假点时，根据对称性，考虑两种子情况。

其一，如果v1,v2是假点，则 f1必定为5+-面（否则与NIC-平面图的定义矛盾），此时若 f3是5+-面，则根据（R4）有：

若 f3是4-面，则其必定为假4-面，由（R2）与（R4）得：

其二，如果v1,v3是假点，则当 f1,f2,f3,f4均为4+-面时，由（R2）与（R4）可得式（4）。当它们中有至少2个3-面时，则其中至少有2个5+-面，故由（R4）得：

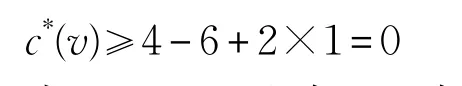
当 f1,f2,f3,f4中有且只有1个3-面时，则其中有2个4+-面与1个5+-面，从而根据（R2）与（R4）有：

（3）当v在GX中的邻点中有且仅有3个假点时，不妨设其为v1,v2,v3，此时若 f1,f2,f3,f4均为4+-面时，由（R2）与（R4）得式（4）。若 f1,f2,f3,f4中存在3-面时，则其必为 f3或者 f4，不妨设其为 f4。现 f3为4+-面且f1,f2为5+-面，故由（R2）与（R4）得：

（4）当v在GX中的邻点中有4个假点时，则其关联4个 4+-面，从而由（R2）与（R4）得式（4）。

情况3点v是5-点

记v1,v2,v3,v4,v5为点v在GX中的5个邻点，并且 f1,f2,f3,f4,f5分别为与{vv1,vv2},{vv2,vv3},{vv3,vv4},{vv4,vv5},{vv5,vv1}关联的面。如果 5个面中至少有3个4+-面，则根据（R3）可得：

否则这5个面中至少有3个3-面，并且其中2个必定相邻。因此不妨设 f1,f2为3-面，由于图G的围长至少为5，故 f1,f2都为假3-面。此时有两种情况：其一，当v2是假点时，则v1,v3为真点，从而vv1v3构成了G中的一个三角形，矛盾；其二，当v2是真点时，则v1,v3为假点，此时|θ(v1)⋂θ(v3)| ≥2，与NIC-平面图的定义矛盾。

情况4面 f是4-面

由于图G的围长至少为5，故 f是假4-面。再由于图是NIC-平面的，其恰好关联1个假4-点。此时如果 f关联（至少）2个真4-点，其必定关联1个5+-点，并且这2个真4-点与 f所关联的假4-点相邻，于是根据（R1），（R2）与（R3），有：

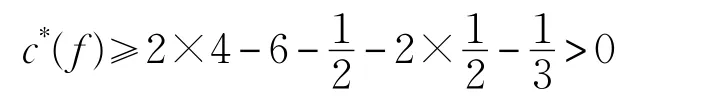
若 f关联恰好1个真4-点，则由前3条规则可得：

若 f不关联真4-点，则由（R1）与（R3）可得：

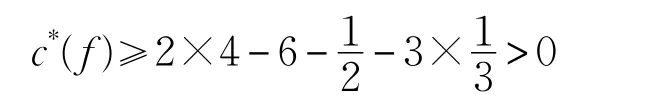
情况5面 f是5+-面

当 d(f)=5时，则根据（R3）、（R4）与（R5）可知当 f关联2个真4-点，2个假4-点与1个5-点时，f向外转移的权值最多，从而：

当d(f)=d≥6时，设 f关联a个真4-点与b个假4-点。因为真4-点与真4-点不相邻并且假4-点与假4-点不相邻，因此根据（R3）、（R4）与（R5）可知：

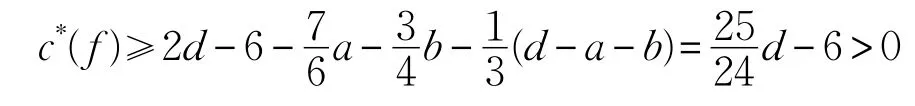
最后，由于6+-点与3-面不参与权转移，故它们的最终权值和初始权值相同，为非负。

至此，已经证明了图GX中的所有点与面的最终权值均为非负，即得到：

由于权只在图GX中的所有点与面的内部进行转移，故转移前后的总权值和不变，即根据式（3）有：

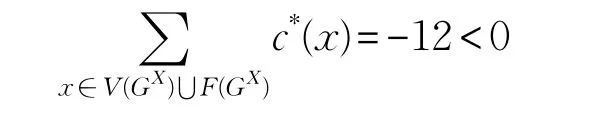
此与式（5）矛盾。

3　结论的推广及其在定向染色中的应用

本章首先给出定理1的一个重要推论。

推论1设G是一个围长至少为5的NIC-平面图，则G存在一个度数至多为3的点，或者两个相邻的度数为4的点。

证明 如果图G不存在度数至多为3的点，则δ(G)≥4。另一方面，由第1章最后一段的分析可知δ(G)≤4，于是δ(G)=4。此时根据定理1可知图G含有两个相邻的度数为4的点。

设G是一个简单无向图，现将图G的每一条边uv进行定向（令u指向v或者v指向u）得到一个有向图。图的一个定向k-染色指的是一个从V到{1,2,…,k}的映射c，其对于图的每一条弧满足：（1）c(u)≠c(v)；（2）不存在弧使得c(x)=c(u)且c(y)=c(v)。从而使得图具有一个定向k-染色的最小整数k称为图的定向染色数，记为χo。设Θ(G)为对无向图G进行定向后得到的所有可能的有向图的集合，则无向图G定向染色数定义为

2007年，Esperet与Ochem[14]证明了如果图G是不满足χo(G)≤67的极小反例，则图G不含有度数至多为3的点，亦不含有两个相邻的度数为4的点。因此，根据推论1可得到如下一个结果。

定理2设G是一个围长至少为5的NIC-平面图，则 χo(G)≤67。

注意到Raspaud与Sopena[15]证明了每个平面图G满足χo(G)≤80，这也是到目前为止最好的结果。由于NIC-平面图类包含平面图类，故从一定的意义上来看定理2是上述结论的推广与改进。

4　结论

综上所述，本文证明了每个围长至少为5且最小度为4的NIC-平面图含有一条边，其2个顶点的度数都是4，从而推出每个围长至少为5的NIC-平面图的定向染色数至多为67。

定理1中，关于NIC-平面图的围长的下界5是否可以降低是一个值得继续考虑的问题。此外，利用其他方式得到NIC-平面图的定向染色数的较好上界也是一个有意义的研究方向。

参考文献：

[1]Zhang X.Drawing complete multipartite graphs on the plane with restrictions on crossings[J].Acta Mathematica Sinica：English Series，2014，30（12）：2045-2053.

[2]Kotzig A.Contribution to the theory of Eulerian polyhedra[J].Mat Čas SAV：Math Slovaca，1955，5：111-113.

[3]Fabrici I，Madaras T.The structure of 1-planar graphs[J].Discrete Mathematics，2007，307：854-865.

[4]Hudák D，Šugerek P.Light edges in 1-planar graphs with prescribed minimum degree[J].Discussiones Mathematicae Graph Theory，2012，32（3）：545-556.

[5]田京京，聂玉峰.度限制条件下的IC平面图类中轻弦4-圈的存在性[J].计算机工程与应用，2016，52（20）：26-28

[6]Zhang X.Light 3-cycles in 1-planar graphs with degree restrictions[J].Bulletin of the Korean Mathematical Society，2014，51（2）：511-517.

[7]Tian J，Zhang X，Light triangles in plane graphs with nearindependent crossings[J].Utilitas Mathematica，2015，97：399-405.

[8]Zhang X.A note one the weight of triangle in 1-planar graphs with minimum degree 6[J].Utilitas Mathematica，2014，93：129-134.

[9]Zhang X，Liu G.On the lightness of chordal 4-cycle in 1-planar graphs with high minimum degree[J].Ars Mathematica Contemporanea，2014，7（2）：233-243.

[10]Zhang X，Liu G，Wu J.Light subgraphs in the family of 1-planar graphs with high minimum degree[J].Acta Mathematica Sinica：English Series，2012，28（6）：1155-1168.

[11]Zhang X，Wu J，Liu G.New upper bounds for the heights of some light subgraphs in 1-planar graphs with high minimum degree[J].Discrete Mathematics and Theoretical Computer Science，2011，13（3）：9-16.

[12]张欣，刘桂真，吴建良.1-平面图的结构性质及其在无圈边染色上的应用[J].中国科学：数学，2010，40（10）：1025-1032.

[13]Bondy J A，Murty U S R.Graph theory with applications[M].New York：North-Holland，1976.

[14]Esperet L，Ochem P.Oriented colorings of 2-outerplanar graphs[J].Information Processing Letters，2007，101：215-219.

[15]Raspaud A，Sopena E.Good and semi-strong colorings of oriented planar graphs[J].Information Processing Letters，1994，51（4）：171-174.