基于云模型求解属性权重的DEMATEL方法研究

谢　晖，李松月，孙永河，韩　玮

XIE Hui,LI Songyue,SUN Yonghe,HAN Wei

昆明理工大学 管理与经济学院，昆明 650093

Faculty of Management and Economics,Kunming University of Science and Technology,Kunming 650093,China

1　引言

多属性决策（Multi-Attribute Decision Making，MADM）是指决策者根据已知的决策信息运用合理的方式、方法对有限的候选方案进行排序择优的过程[1]。多属性决策研究包括两个部分内容：一是决策数据的获取，二是备选方案的排序择优[2]。决策数据通常包括属性值与属性权重值，属性值是决策专家给出的每个方案关于各个属性的评估值；而属性权重值则反映了各指标在决策中所处的地位。属性权重的确定直接影响到决策的质量和效果，因而有关属性权重的研究一直是多属性决策中的热点和难点问题，也取得了诸多的研究成果[3-11]。迄今有关确定属性权重的方法主要分为三类：

方法一，客观赋权法，该方法是在属性值已知的情况下确定权重，通常采用的方法有目标规划法[12-13]、离差最大法[14-15]、熵权法[16-18]、基于贴近度法[19-20]、线性规划法[21-22]、基于方案满意度法等[23]；方法二，主观赋权法，该方法则是依据决策专家的个人偏好给定权重信息，常用的方法有判断矩阵法[24]、属性重要性排序法[25-26]、估计值法[27]等；方法三，混合赋权法，该方法则将前述两种方法相结合对属性权重予以判定，较为常见的方法有方差最大赋权法[28-29]、组合目标规划法[30-31]等。上述三种方法各有利弊，主要表现在：方法一具有能够对已知信息客观处理的优势，但不能充分体现出决策者对各属性的主观认知程度；方法二简单易行，但完全依赖于专家的个人知识、经验，可能会忽略一些潜在的有价值的信息，具有较强的主观随意性；方法三能够兼顾上述两种方法的优点，但三种方法都忽视了在面对复杂问题进行决策时各个属性之间存在的复杂关联关系。事实上，基于复杂系统思维观对决策问题剖析，系统认知各属性之间的复杂因果联系，对属性的重要性予以清晰辨析，探索属性权重机理的内生复杂性，对有效提升决策质效具有重要的理论和实践应用价值。

通过梳理现有文献可以发现，在确定属性权重时，深入研究复杂问题决策情境下属性间相关关系的文献较少，鉴于此，本文针对属性权重完全未知的多属性决策问题，充分考虑决策中的模糊性与随机性，提出一种基于云模型的DEMATEL方法确定属性权重。

2　相关理论基础及方法构建思路

2.1　系统思维观

复杂性科学是21世纪的科学，是整个科学发展的前沿[32]。钱学森曾反复告诫人们，因为复杂，所以一定要用系统概念，在论及有关地理、军事、人体、社会等复杂问题时，则更需应用开放复杂巨系统这个系统科学的核心概念[33]。系统科学界早已形成普遍的认知：将研究对象作为系统来认识，从不同视角、不同层次揭示其系统的内涵。而系统思维正是运用系统的概念来认识对象、整理思想的思维方式[34]。对系统的理解需要把握其本身所具有的三个特征[35]：一是多样性，包括多元性和差异性，承认和尊重差异性与多样性，这是系统思维的基本要求；二是相关性，即多样性的系统要素彼此之间存在着相互依赖、相互制约、相互作用的关联关系；三是一体性，即系统中的要素具有特定的关联方式与关联强度，作为一个统一体按照一定规律运行并与外界发生相应的关系。系统思维要求人们从整体上认识和解决问题，在复杂情境下多属性决策问题所具有的各类属性，都无法脱离复杂问题本身而单独存在，且彼此之间存在着千变万化的联系。因此，在系统思维观下剖析复杂问题中的多属性决策问题，实际上是将原来在分析思维观下（还原论）求解属性权重时，把割裂开来孤立研究的属性指标作为一个系统予以探索，将整体思维与分析思维相结合，把对复杂问题的认知建立在各属性精细认知的基础之上，充分考虑各指标之间的关联性，从而使得属性权重的求解更具科学性。

2.2　新方法构建思路

分析传统DEMATEL的内在机理可知该方法中专家对因素之间的影响强度予以判断时存在着较强的不确定性，这是由于客观世界的复杂性和多变性使决策者获得的信息本身就是不确定、不完全、不一致的。对已获得知识认知上的复杂与局限性及思维过程的主观性是决策者决策不确定性的主要原因，具体表现在：一是对决策问题以及属性概念认知的理解不够清晰，模型、概念本身是对现实世界的抽象。决策者需要具备全面专业的相关背景知识才能对所要决策的信息给出合理、科学的判断。二是在信息处理过程中，由于专家经验常识（元知识）、思维习惯、专业背景、风险偏好等原因也会对决策结果产生难以预计的影响。三是语言评价的不确定性，不同决策者对决策工具的评价语言会因为习惯的影响而给出与实际情况偏差较大的评判标准。四是模糊性与随机性并存，属性会随着决策问题的变化呈现出不同的特征，模糊性与随机性同时出现成为常态，难以辨识。依据上述理论认识，本文选取基于云模型的DEMATEL方法确定属性权重指标，即专家的偏好通过云模型的方式实现定性到定量的转化。云模型是李德毅教授在随机数学与模糊数学基础上提出的，实现定性与定量之间相互转换的不确定性转换模型[36]。该模型反映了自然语言表述的不确定性理解，使语言表述的随机性、模糊性与二者之间的关联性通过云的三个数字特征有机结合起来，具有普适性与直观性。云模型从自然语言出发，将定性概念转化为论域空间里的点，即获取定量数据的分布范围与分布规律，论域空间中的点的选择是随机的，以其概率分布函数描述。每个定性概念都包括多个云滴，每个云滴都表示该定性概念映射到数域空间的点，是语言值在数量上的实现，云滴的产生具有随机性，且云滴的确定度也具有模糊性。

为此新方法的构建思路为：针对某一决策问题的属性权重求解，首先确定选取简单易懂的五级标度的自然语言描述方式表达个人的偏好（选取该种描述方式一方面由于自然语言更加贴近个体的表达方式，更易于做出正确选择，另一方面是当属性指标数量较多时，过多的语言评价标度会使评价本身过于繁琐，专家难以专注于决策问题本身，从而影响决策的合理性与科学性）。接下来由专家对属性间关联关系做出评判，并转化为云模型的表达形式。之后对各专家的影响矩阵信息予以集结，并测度综合影响矩阵（TIM）。最后依据TIM求解各属性的中心度与综合权重。

2.3　基本理论与概念

2.3.1云模型基本理论

定义1[37]云是连接自然语言表述的定性概念与其对应的定量表示之间的不确定性的转换模型。设U是一个定量论域，U={x}，C是与U相联系的空间上的定性概念，对于U中的元素x，在C中都存在一个具有稳定倾向的随机数μ(x)，则称x为C的隶属度，隶属度在论域上的分布称为隶属云，简称为云，每个x称为云滴。μ(x)取值范围为[0,1]，云是定性概念C从论域U到区间[0,1]的映射，即：μ(x):U→[0,1],∀x∈U,x→μ(x)。

如果用数字特征来反映定性概念的定量特性[38]，以期望 Ex（Excepted Value）、熵 En（Entropy）、超熵 He（Hyper Entropy）这三个数字表示其整体特征。

期望Ex：在论域空间中最能够代表定性概念的点，是论域空间分布的期望值，代表着定性语言概念中论域的中心值。

熵En：对定性概念的不确定性度量。一是表示该概念下被接受的云滴的取值范围；二是反映该概念下所有云滴的离散程度，是对随机性的反映。

超熵He：熵的熵，是对熵(En)的不确定性量度，熵的模糊性与随机性决定超熵。

2.3.2不确定性语言描述

定义2[39]决策者进行定性评价时，要借助于恰当的语言评估标度，设定其语言标度集合为：S={si|i=-t,…,t,t∈N}，si表示用于测度的语言变量，s-t和st则代表决策者使用的语言变量的上限与下限，满足下述条件：

（1）α＞β 时，有 sα＞sβ。

（2）存在负算子neg(sα)=s-α。

（3）若 sα＞sβ，有 max{sα,sβ} =sα。

（4）若 sα＜sβ，有 min{sα,sβ} =sα。

2.3.3云模型的基础运算

2.3.4不确定性语言值的云模型转换

定义7[45]将定义3中不确定性语言值[sα,sβ] 转化为两朵云，称为左云 sα→yα=(Exα,Enα,Heα)和 右 云sβ→yβ=(Exβ,Enβ,Heβ)，两朵云集结后的云为综合云yˉ=(Ex,En,He)。当两朵云期望间距足够大，相交为空集 (yα⋂yβ=∅)时，有|Exβ-Exα|＞3|Enβ-Enα|，则生成的综合云的数字特征为：

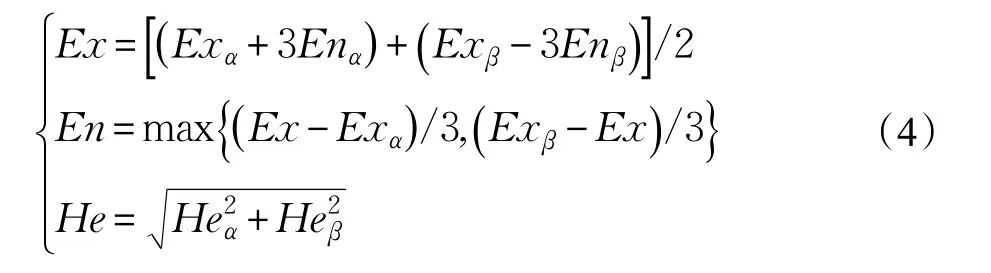
3　新方法模型的构建

依据上述理论思想，给出一种基于云模型的求解属性权重的DEMATEL方法步骤如下。

步骤1确定系统的影响因素（属性）集合为G={g1,g2,…,gn} 。

步骤2绘制属性关联关系图。邀请决策专家组对属性间的相互影响关系予以判断，若属性gi对gj有直接影响，则在二者之间标记一条由gi指向gj的箭头，以此类推，绘制所有属性间的关联关系有向图。

步骤3构造专家判断的初始直接影响矩阵。选取五级语言标度，并请每位专家依据给定的语言标度{非常弱(s-2)，弱(s-1)，一般(s0)，强(s1)，非常强(s2)}对属性间相互影响强度予以判断。假设决策组中有F={fi|i=1,2,…,u}位决策专家，专家 fk的初始直接影响矩阵 Hk为：Hk=[hij]n×n，当属性 gi对 gj有直接影响时，令hij=[si,sj](i,j=-2,-1,0,1,2)，若无影响记hij为零，该矩阵主对角线元素都为零。

步骤4转化决策信息。利用公式（4）、（5）将决策者给出的不确定性语言值转化为综合云的表达形式yˉ=(Ex,En,He)，将专家 fk对属性间相互影响关系的判断矩阵Hk转化为Hˉ()k：

步骤5确定决策者权重。在式（6）中，ω1,ω2,…,ωn原表示属性权重，转化为DEMATEL问题，ωi(i=1,2,…,n)表示决策者权重，即在给出的DEMATEL评价矩阵中，专家 fk偏好集结权重为 ωk，基于式（2）、（3）中决策者不确定度和偏差度求出决策者权重，具体为：决策者 fk的第一个客观权重为：决策者 fk的第二个客观权重为：

设两个权重的不同风险偏好分别为α和β，进而计算得出决策者 fk的最终权重为：β≤1,α+β=1。

步骤6集结全体专家的影响矩阵。依据步骤5求出的决策者权重，基于式（6）集结所有专家的群体信息，得到信息集结后的综合云矩阵Hˉ(k)′。

步骤7计算专家综合云评价矩阵各云与正负理想评价云的Hamming距离，由式（7）可得正理想评价云：y+=(maxExi,minEni,minHei)，负理想评价云为：y+=(minExi,maxEni,maxHei)。计算每个属性相互影响强度评价云与正负理想评价云的Hamming距离分别为：，得到属性间影响关系强度矩阵

步骤8规范化集结后的影响矩阵D。根据公式可得标准化的直接影响矩阵M，M中对角线元素取值为0。

步骤9测度综合影响矩阵。依据公式Z=M(IM)-1=(zij)n×n测度各属性与其他属性的直接和间接影响后形成的综合影响矩阵Z，I为单位矩阵。

步骤10计算各属性的中心度与原因度。将矩阵Z中的各元素按行相加，得到对应属性的影响度为按列相加则得到对应属性的被影响度为将二者相加得到界面在评价系统中的重要程度，即中心度oi：oi=fi+qi(i=1,2,…,n)。

步骤11确定各属性的影响权重。由各属性的中心度oi可知每个属性在系统中所处的位置，即相对重要性，归一化后可得到各属性的影响权重为ki：ki=

表1　基于DEMATEL的综合云矩阵Hˉ(k)′

4　案例应用

以K大学三个创新团队(a1,a2,a3)为例，对创新团队的融合度予以评价，属性指标分别为团队文化认同感(c1)、团队沟通管理(c2)、团队正式管理制度(c3)、非正式制度(c4)、激励类型多样化(c5)、激励公平性(c6)六个指标。首先邀请五位专家根据给定的语言标度{非常弱(s-2)，弱 (s-1)，一般 (s0)，强 (s1)，非常强 (s2)}对六个属性指标间的相互影响关系予以判断，并转化为相应的云模型，在求解得到决策者权重ω=(0.39,0.16,0.25,0.10,0.10)之后，集结五位专家信息，得到综合云矩阵见表1。依据综合云矩阵，求解可得正负理想评价云为y+=(90.73,4.73,0.21)，y_=(47.33,10.93,0.45)，分别求出综合云矩阵中每朵云与正负理想评价云的Hamming距离与，得到属性间影响关系矩阵。按照步骤8～11求解得出各个属性的影响权重，如表2所示。

表2　各属性影响度、被影响度、中心度与属性权重

依据表2，经五位决策专家评价可知，在创新团队的融合度评价中，团队的正式管理制度与激励公平性所占权重最大，即在属性指标系统中这两类指标最为重要，接下来依次为沟通管理、非正式管理制度、激励类型多样化以及文化认同感。通过上述分析可知，在创新团队的实践管理中，对其进行评价的各属性指标之间存在着千丝万缕的联系，甚至在某些复杂情境中发生转化，如团队成立初期的某些不成文的约束在团队日益成熟之后会转化为正式管理制度指导团队成员的行为；又如激励形式的多样化会对激励公平性有着正向的影响，能够激发团队成员的内在动机。DEMATEL决策方法克服了原有属性权重确定方法中忽略属性因素关联关系的缺陷，且通过云模型将定性转化为定量的方式能够较好地转化决策者的不确定语言信息，融合决策过程中的随机性与模糊性，从而为辨析属性间的复杂关联关系奠定了基础。同时，通过与专家交流，认为自然语言评价更符合逻辑思维模式，能够较为准确地给出属性影响关系与影响强度，且所得结果能够较好地提供决策依据，方法具有实际应用可行性。

5　结论

多属性决策方法中，有关属性权重的求解问题一直以来受到学术界的广泛关注。本文在复杂系统思维观的视角下，提出了一种基于云模型来确定属性权重的DEMATEL方法，相较于现有文献中的主观、客观、主客观结合赋权法，具有以下优点：（1）针对多属性群决策中属性权重信息完全未知的情境，提出了采用DEMATEL方法来确定属性权重。该方法基于系统思维观，即运用系统整体性认知的概念来认识研究对象，充分考虑了属性权重作为系统要素所具备的多样性、相关性和一体性，将所有属性指标视为一个系统，从而使得属性权重的求解更加符合现代决策的复杂性，也更具科学性与客观性。（2）针对决策专家的偏好表达习惯，选取自然语言的五级标度形式，一方面能够更加贴近个体的表达习惯，更易于做出正确的选择，另一方面简洁的标度级数使专家能够更加专注于实际决策问题与决策情境，避免陷入繁琐的标度辨识中而忽略主要问题的解决。（3）基于云模型理论实现了由定性到定量的转化，既兼顾了语言评价的便利性及存在的不确定性，也使得语言评价的模糊性与随机性通过云模型有机结合起来，细腻地刻画了复杂决策的模糊性与不确定性本质，更具直观性与普适性。最后，通过一个实例的验证结果表明，本文所提出的方法是科学合理的，能够有效解决具有复杂关联关系的属性权重求解问题。

参考文献：

[1]Xu Z，Yager R R.Dynamic intuitionistic fuzzy multi-attribute decison making[J].International Journal of Approximate Reasoning，2008，48（1）：246-262.

[2]徐泽水.不确定多属性决策方法及应用[M].北京：清华大学出版社，2004.

[3]Xu Z，Yager R R.Intuitionistic and interval-valued intutionistic fuzzy preference relations and their measures of similarity for the evaluation of agreement within a group[J].Fuzzy Optimization&Decision Making，2009，8（2）：123-139.

[4]Wan S P，Xu G L，Wang F，et al.A new method for Atanassov’s interval-valued intuitionistic fuzzy MAGDM with incomplete attribute weight information[J].Information Sciences，2015，316：329-347.

[5]Jiao H，Wang S.Multi-attribute decision making with dynamic weight allocation[J].Intelligent Decision Technologies，2014，8（3）：225-230.

[6]Danielson M，Ekenberg L，He Y.Augmenting ordinal methods of attribute weight approximation[J].Decision Analysis，2014，11（1）：21-26.

[7]Liu X D，Zhu J J，Zhang S T，et al.Hesitant fuzzy multiple attribute decision making method based on optimization of attribute weights[J].Control&Decision，2016，31（2）：297-302.

[8]Luo D，Li Y.Multi-stage and multi-attribute risk group decision-making method based on grey information[J].Grey Systems Theory&Application，2015，5：222-233.

[9]Zhou L，Merigó J M，Chen H，et al.The optimal group continuous logarithm compatibility measure for interval multiplicative preference relations based on the COWGA operator[J].Information Sciences，2016，328：250-269.

[10]Zhou L，Chen H，Liu J.Generalized multiple averaging operators and their applications to group decision making[J].Group Decision&Negotiation，2013，22（2）：331-358.

[11]Zhou L，Chen H.Generalized ordered weighted proportional averaging operator and its application to group decision making[J].Informatica，2014，24（2）：327-360.

[12]Wang Z J，Li K W，Wang W Z.An approach to multiattribute decision making with interval-valued intuitionisitc fuzzy assessments and incomplete weights[J].Information Sciences，2009，179（17）：3026-3040.

[13]万树平，董九英.基于三角直觉模糊数Choquet积分算子的多属性决策方法[J].中国管理科学，2014，22（3）：121-129.

[14]Wei G W.Maximizing deviation method for multiple attribute decision making in intuitionistic fuzzy setting[J].Knowledge-Based Systems，2008，21：833-836.

[15]徐泽水.区间直觉模糊信息的集成方法及其在决策中的应用[J].控制与决策，2007，22（2）：215-219.

[16]刘满凤，任海平.基于一类新的直觉模糊熵的多属性决策方法研究[J].系统工程理论与实践，2015，35（11）：2909-2916.

[17]戚筱雯，梁昌勇，张恩桥，等.基于熵最大化的区间直觉模糊多属性群决策方法[J].系统工程理论与实践，2011，31（10）：1940-1948.

[18]Zhang H，Yu L.MADM method based on cross-entropy and extended TOPSIS with interval-valued intuitionistic fuzzy sets[J].Knowledge-Based Systems，2012，30（2）：115-120.

[19]朱丽，朱传喜，张小芝.基于粗糙集的犹豫模糊多属性决策方法[J].控制与决策，2014，29（7）：1335-1339.

[20]戴泉晨，朱建军.不完全类别信息下多属性决策的案例学习方法[J].系统工程，2016，34（3）：129-134.

[21]杨静，邱菀华.基于投影技术的三角模糊数型多属性决策方法研究[J].控制与决策，2009，24（4）：637-640.

[22]陈晓红，胡文华，曹裕，等.基于梯形模糊数的分层多目标线性规划模型在多属性不确定决策问题中的应用[J].管理工程学报，2012，26（4）：192-198.

[23]徐泽水，孙在东.一种基于方案满意度的不确定多属性决策方法[J].系统工程，2001，19（3）：76-79.

[24]李继乾，郝颖娟.不同直觉偏好信息下的多属性决策方法[J].数学的实践与认识，2012，42（3）：19-25.

[25]孙昭旭，韩敏.不完全信息下的群体多属性决策方法[J].系统工程与电子技术，2007，29（7）：1098-1101.

[26]茹保锋，张存禄.基于决策者预期的多属性决策方法[J].统计与决策，2013（18）：23-25.

[27]毛红保，张凤鸣，冯卉，等.一种基于区间估计的多属性决策组合赋权方法[J].系统工程理论与实践，2007，27（6）：86-92.

[28]王霞，党耀国.基于Choquet积分的区间灰数多属性决策方法[J].系统工程与电子技术，2015，37（5）：1106-1110.

[29]吴群，吴澎，周礼刚.基于联系数的区间二元语义模糊多属性群决策方法[J].重庆工商大学学报：自然科学版，2016，33（1）：1-8.

[30]Liao H，Xu Z，Zeng X J.Distance and similarity measures for hesitant fuzzy linguistic term sets and their application in multi-criteria decision making[J].Information Sciences，2014，271（3）：125-142.

[31]王鹏飞，李畅.不确定多属性决策双目标组合赋权模型研究[J].中国管理科学，2012，20（4）：104-108.

[32]沃尔德罗普.复杂：诞生于秩序与混沌边缘的科学[M].陈玲，译.北京：三联书店，1997.

[33]钱学森.论地理科学[M].杭州：浙江教育出版社，1994.

[34]苗东升.系统思维与复杂性研究[J].系统科学学报，2004，12（1）：1-5.

[35]苗东升.论系统思维（一）：把对象作为系统来识物想事[J].系统科学学报，2004，12（3）：3-7.

[36]张玉芳，谢娟，熊忠阳.一种结合云模型的文本分类方法[J].计算机工程与应用，2014，40（15）：117-119.

[37]Li D Y.Artificial intelligence with uncertainty[M].Beijing：National Defense Industry Press，2005.

[38]Li D Y，Liu C Y.Study on the universality of the normal cloud model[J].Engineering Science，2004，6（8）：28-34.

[39]Herrem F，Herrera-Viedma E，Verdegay J L.Rational consensus model in group decision making using linguistic assessments[J].Fuzzy Sets and Systems，1997，88（1）：31-39.

[40]Xu Z S.Induced uncertain linguistic OWA operators applied to group decision making[J].Information Fusion，2006，7（2）：231-238.

[41]Xu Z S.Uncertain linguistic aggregation operators based approach to multiple attribute group decision making under uncertain linguistic environment[J].Information Sciences，2004，168（1/4）：171-184.

[42]Yager R R.OWA aggregation over a continuous interval argument with applications to decision making[J].IEEE Transactions on Systems Man&Cybernetics：Part B Cybernetics，2004，34（5）：1952-1963.

[43]Xu Z S.Deviation measures of linguistic preference relations in group decision making[J].Omega，2005，33（3）：249-254.

[44]Herrera F，Herrera-Viedma E，Martı´Nez L.A fusion approach for managing multi-granularity linguistic term sets in decision making[J].Fuzzy Sets&Systems，2000，114（1）：43-58.

[45]王坚强，刘淘.基于综合云的不确定语言多准则群决策方法[J].控制与决策，2012，27（8）：1185-1190.