近邻搜索在多孔材料格点模型建模中的应用
刘任涛,陈 卫
LIU Rentao1,2,CHEN Wei1
1.中国科学院 计算机网络信息中心 高性能计算技术与应用发展部,北京 100190
2.中国科学院大学,北京 100049
1.Department of High Performance Computing Technology and Application Development,Computer Network Information Center,ChineseAcademy of Sciences,Beijing 100190,China
2.University of ChineseAcademy of Sciences,Beijing 100049,China
1 引言
分治算法是计算机领域中一种广为人知的算法,它的功能体现在于两个方面:其一,通过多次的递归迭代自动地将复杂的问题分解成许许多多小问题;其二,将每个小问题的解沿着分解该问题的逆方向合并,直到得到原问题的解[1]。分治算法实现这两个功能的具体方式在于将程序段多次递归迭代。近年来,由于能够以相对简单的程序段解决复杂的问题,分治算法的分而治之的思想被运用在诸多领域:例如在计算机科学领域利用分治算法研究聚类问题和群体智能算法[2-3];在计算机图形学领域利用分治策略划分Delaunay三角网格[4-5];在数值计算领域利用分治算法求矩阵特征值[6-7];在系统科学领域利用分治算法研究种群的进化[8]。然而分治策略很少被应用于与计算物理和化学物理相关的计算机模拟当中。
多孔材料是一种具有非均匀内部结构的系统,在物理学[9-12]、化学[13]、材料科学[14]等领域引发了越来越多研究者的关注。将多孔材料体系离散为格点系统来进行计算机模拟是一种高效的计算机模拟方法,在基础研究领域不断涌现出新成果[15-16]。多孔材料的内部由两部分组成:一部分是母体,被固体物质填充;另一部分是孔隙,可以容纳流体(例如气体和液体)。多孔材料格点模型(Porous Material with Lattice Model,PMLM)的计算机模拟分为初始化建模和体系演化两个步骤,其中的初始化建模步骤需要把全体空间中的格点区分为两类进行标记:一类格点标记为母体填充物(例如固体);另一类格点标记为材料当中的孔隙。然而在实际研究过程中,对格点进行分类的过程并不是完全随机的。为了逼近真实物理体系,通常母体区块采用具有硬球势或Lennard-Jones势的球体[9,15]。原始建模方法不得不在固定每一个母体球的条件下遍历地搜索全体空间的每一个格点,其计算量与系统体积的平方成正比。随着模拟体系规模的增大,计算机模拟过程中的初始化建模步骤的计算量急剧增加,这是许多关于大规模多孔材料的研究无法承受的。
k近邻搜索是一种用来取代全空间遍历搜索的高效的搜索方式,在模式识别、机器学习、数据挖掘、时间序列分析等方面有诸多应用。利用k近邻搜索可以预测数据样本的分类,或以较小的代价寻找目标样本[17-20]。受到k近邻分类算法的启发,本文把基于分治策略的近邻搜索(Divide-Conquer based Nearest-Neighbor searching,DCNNs)方法应用到PMLM的建模当中,详细介绍了在PMLM系统中应用DCNNs建模的方法。本文还在理论和实验上对原始建模方法和DCNNs建模方法的运行效率作了比较。
2 基于分治策略的近邻搜索方法理论
2.1 PMLM系统的基于分治策略近邻搜索的优化建模方法
在一个三维格点模型中,格点的编号遵循:首先沿x方向布满再向y方向延拓,布满每一个xy平面后再向z方向延拓。因此,只要得到一个格点的序号就可以知道该格点在三维体系中的坐标(x,y,z);反之,根据任意一个格点的坐标就可以知道该格点的序号。
多孔材料的显著特征就是构型当中的母体物质与孔隙分散的占据全体空间。最常采用的硬球势体系须将母体区域视为由一个个小球堆叠而成,孔隙区域占据剩余的空间。随机选择一个格点作为一个母体小球的球心A(x0,y0,z0)。为了标记出被球形母体占据的格点,最简单的筛选办法就是首先固定母体球的球心坐标,然后计算各个格点与球心之间的几何距离:

球形母体区域的限制条件:如果某个格点到该球心之间的几何距离di小于设定的母体球半径R,则认为此格点在该母体球内部。
本文提出的DCNNs建模方法是以PMLM的一个母体区域的中心A作为根节点,通过分治的办法将近邻区域的格点划分为不相交的区域,递归地向外部空间扩展以实现近邻搜索。利用该DCNNs可以快速地标记出PMLM当中应当被母体占据的格点。
图1显示了用于PMLM建模过程中的DCNNs在不同类型格点位置上向近邻格点扩展的状态空间图,图中的每一个箭头对应于一个方向上的扩展(体现在计算机程序中就是一个子程序)。算法对应的伪代码如算法1~7所示。
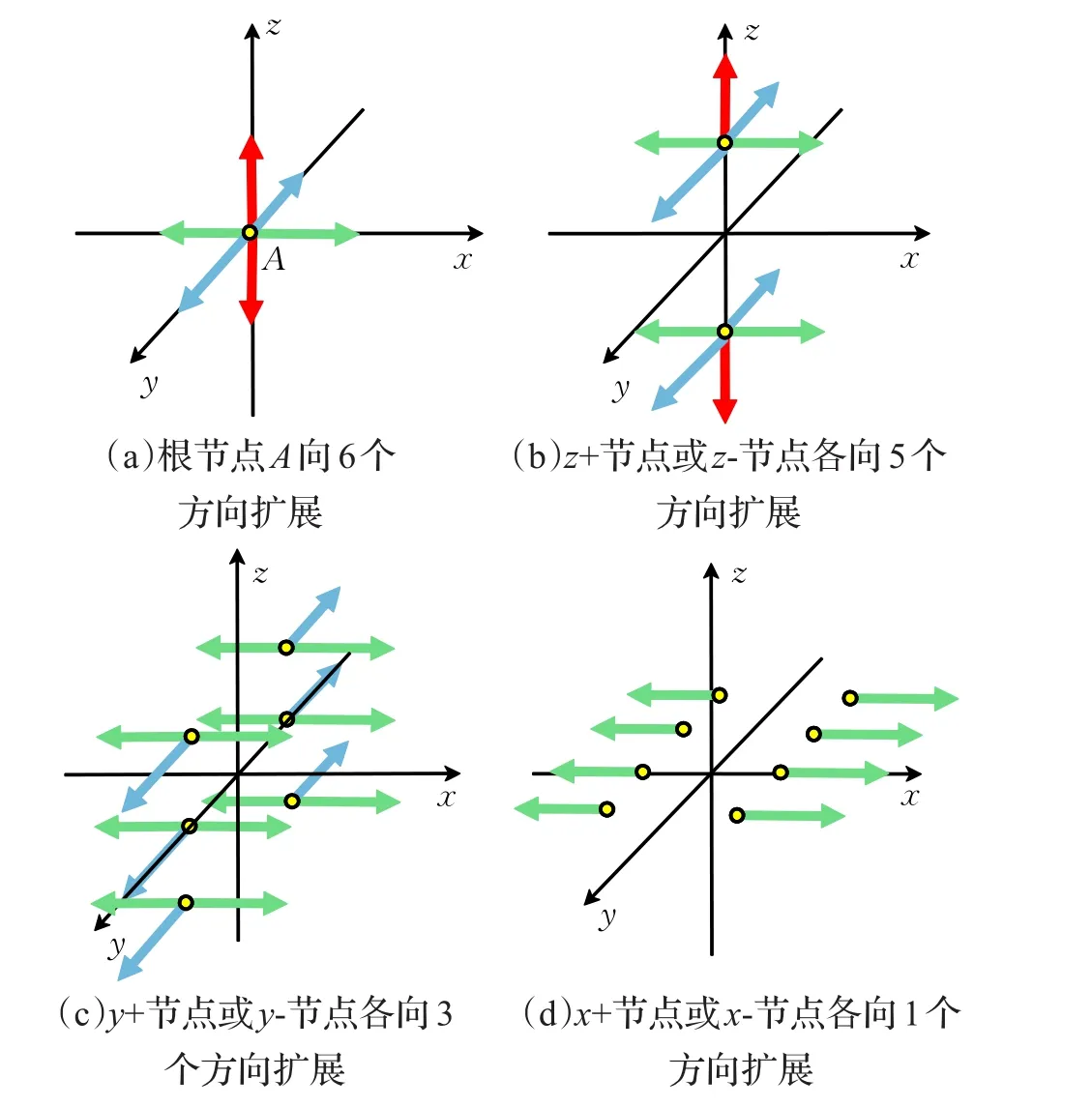
图1 近邻搜索各个格点的状态空间图
伪代码算法1表述了向6个方向扩展根节点的算法,状态空间如图1(a)所示。

伪代码算法2和伪代码算法3分别表述了向5个方向扩展z+节点或z-节点的算法,状态空间如图1(b)所示。
算法 2 UP(z,queue)

伪代码算法4和伪代码算法5分别表述了向3个方向扩展y+节点或y-节点的算法,状态空间如图1(c)所示。


DCNNs过程中的数据结构可以描绘成树状图,如图2所示,除了叶节点以外:
(1)根节点有6个子节点;
(2)每个z+或z-节点有5个子节点;
(3)每个y+或y-节点有3个子节点;
(4)每个x+或x-节点有1个子节点。

图2 三维格点系统的DCNNs的搜索树
从几何空间上看,这样的搜索机制类似于“碰壁”:设想在母体球外包裹了一层球壳,当计算机沿着一条搜索路径向前搜索直到访问到球壳上的格点时返回寻找下一条路径继续搜索。该DCNNs方式在搜索顺序方面类似于深度优先搜索,搜索方向沿着搜索树直到叶节点才返回,一言以蔽之就是“一路到底”。但区别在于:传统的深度优先搜索的目的只是为了找到一个目标节点,因此一旦找到目标节点就会终止搜索;而本文介绍的搜索方法并没有特定的目标节点,只有把搜索树的所有叶节点全部搜索了一遍以后才会终止。
该基于分治策略的近邻搜索方法吸收了数据分割的思想[20],通过将近邻空间格点划分成合理的数据结构,保证了在同一次近邻搜索当中既不会遗漏任何一个应当被搜索到的格点,又不会重复搜索任何一个格点。采用该DCNNs方法对PMLM系统进行建模,能够准确地筛选出初始构型中应当被母体物质占据的格点。此外,只要改变程序中对于球形母体区域的限制条件,就可以将该DCNNs方法推广用来对具有更复杂的母体形状的PMLM系统进行建模。
2.2 建模时间复杂度的理论分析与比较
2.2.1原始方法建模的时间复杂度
对于PMLM系统,原始的算法是:首先随机生成每一个母体区块的球心的坐标,然后在固定该坐标的条件下遍历搜索空间中的所有格点,计算各个格点的坐标与母体球心坐标的空间距离,从而筛选出位于该母体球内部的格点。
不妨设整个PMLM体系的格点总数为N;体系中被母体物质填充的格点个数与格点总数的比例是固定的,设为η(0<η<1);同一体系中的各个母体球的半径大小是相同的,设每个母体球占据n个格点。对于不同的体系,当母体球的半径大小固定不变时,每个母体球中包含的格点个数n也是固定的常数(对于多孔材料n≪N)。格点系统建模过程中的时间复杂度:

2.2.2DCNNs方法建模的时间复杂度
同样,不妨设整个PMLM体系的格点总数为N;体系中被母体物质填充的格点个数与总的格点个数的比例为η(0<η<1);每个母体球占据n个格点(n固定,且n≪N)。对于同样的PMLM系统,基于分治策略的近邻搜索首先也是随机生成每一个母体球的球心的坐标,然后在固定该坐标的条件下利用2.1节当中介绍的规则进行分类,在每一个母体球球心附近搜索到的格点个数,仅仅是母体球理论上包含格点个数n加上母体球外的“壁”包含的格点个数(其数量级一般不高于n具有的数量级)。格点系统建模过程中的时间杂度:

很明显,在理论上,对于n≪N的情形(例如多孔材料),DCNNs方法建模的时间复杂度更低,能够节省大量计算量。
3PMLM系统气液相变的计算机模拟
3.1 Gibbs系综下基于密度泛函的格点模型平均场理论的热力学函数
假定空间被离散化为三维的格点网络,共有N个格点,第i个格点的粒子数密度为ρi,设第i个格点上的外场为Vi,第i、j格点之间的相互作用强度为εij,则整个体系的总势能:
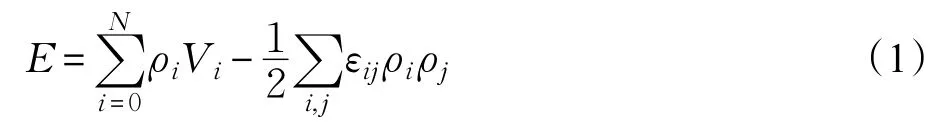
对于经典体系的热力学正则系综(固定的温度、体积、总粒子数),全体粒子所处的密度状态服从热力学统计规律,任意一个给定的粒子数分布{ρi}出现的热力学概率为:

其中,正则系综配分函数:

因此,体系的Helmhotz自由能:
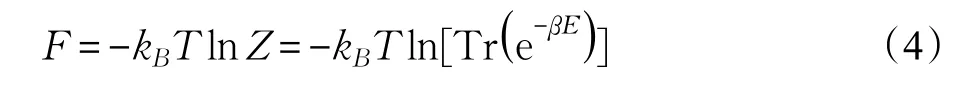
构造一个无外场无相互作用(Vi=0,εij=0)的参考体系,设参考体系的总能量为E͂,则实际体系的能量E可以写为参考体系能量与附加能量ΔE的加和:

在参考体系中,各个热力学构型出现的几率相等:

此时配分函数Z的物理意义可以形象地表述为M个粒子随机分配给N个格点分配方式总个数,即服从超几何分布:

对于M和N的值很大的情形(例如宏观热力学体系),运用Stirling近似ln(N!)≈NlnN-N ,则该参考体系的Helmhotz自由能:
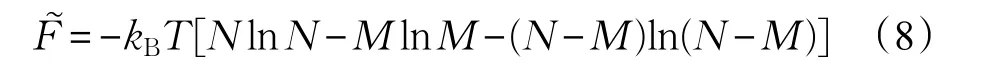
其中,kB是Boltzmann常数,一个关于温度和能量的物理常数。
由于该参考体系的粒子数分布可以视为宏观上均匀的,设参考体系的粒子数密度ρ=M/N,因而该参考体系的Helmhotz自由能:
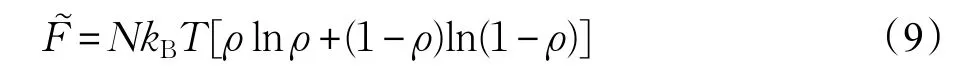
其中的密度ρ是无量纲的约化密度(0<ρ<1)。
引入平均场近似,设外场对每一个格点的作用强度为ϕi,则附加能量可以表示成:
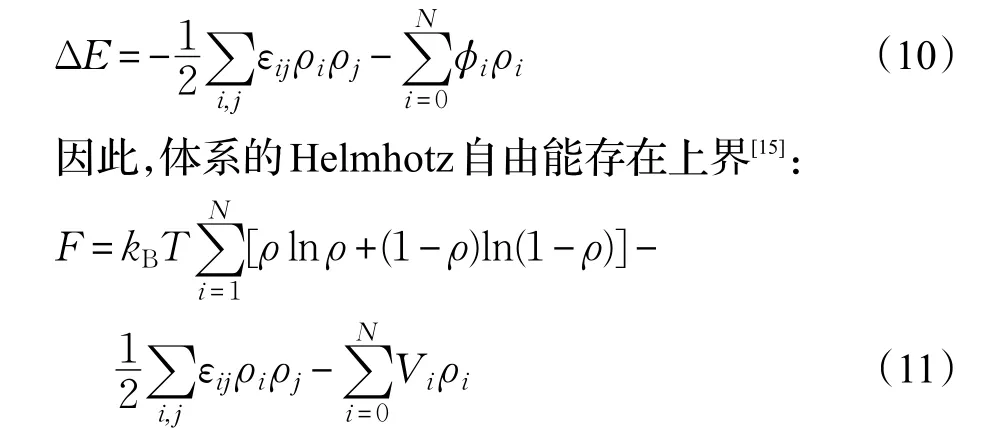
3.2 密度迭代演化的计算机模拟方法
对于实际的物理系统,系统达到平衡时的密度分布使式(11)取得极小值,即满足微分方程:

将格点之间的相互作用当作短程力处理,仅仅考虑最近邻和次近邻格点之间的相互作用[14],并将表达式(11)代入式(12)即可得到达到热力学平衡状态下系统关于密度的代数方程[14]:
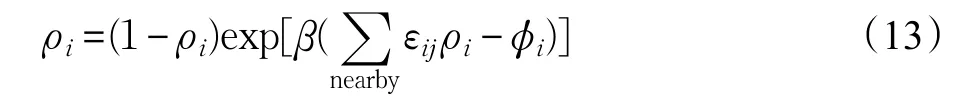
对于每一个格点,每次把旧的密度值代入上式右端,计算结果赋值给等号左端的新的密度值ρrhsi。为了防止密度取值跳动过大以致溢出(必须满足ρ≤1),密度值与旧密度值进行线性组合,使得新得到的密度值仅仅在原有值的基础上小范围改动。因此,整个迭代的完整过程用等式(14)、(15)、(16)表示[14]:
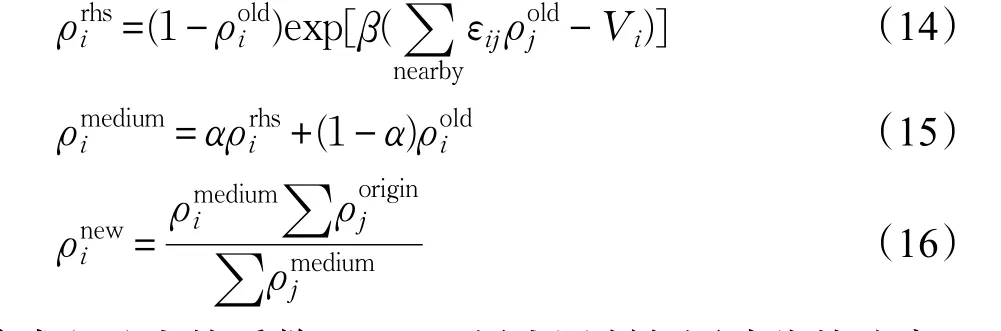
等式(15)中的系数α(α≪1)用来限制每圈迭代的速率;等式(16)用来标定体系的总粒子数守恒,得到每一轮迭代被更新的密度值。
反复迭代等式(14)、(15)、(16),使得系统的密度分布最终收敛。当某一圈迭代过后系统中密度值的改变量大小的平均值小于设定的阈值时,认为体系已经达到热力学近平衡,终止迭代。
3.3 计算机模拟结果的比较
本文对采用周期性边界条件的边界长为50、65、80、100的立方体形格点模型分别进行计算机模拟。使用原始方法和DCNNs方法分别进行建模能够构造相同的初始构型(流体的初始密度均匀ρ=0.28),并经过迭代演化达到同样的热力学平衡态。一个包含106个格点的三维体系的模拟结果,在x=0的截面的密度分布如图3所示。图右侧标出了各种颜色代表的流体密度值(无量纲约化密度0<ρ<1),图中空白区域是建模时建立的母体(流体密度为零),图中密度稠密的团状聚集区域是液相凝聚区,证明该体系已经发生了气液相变。
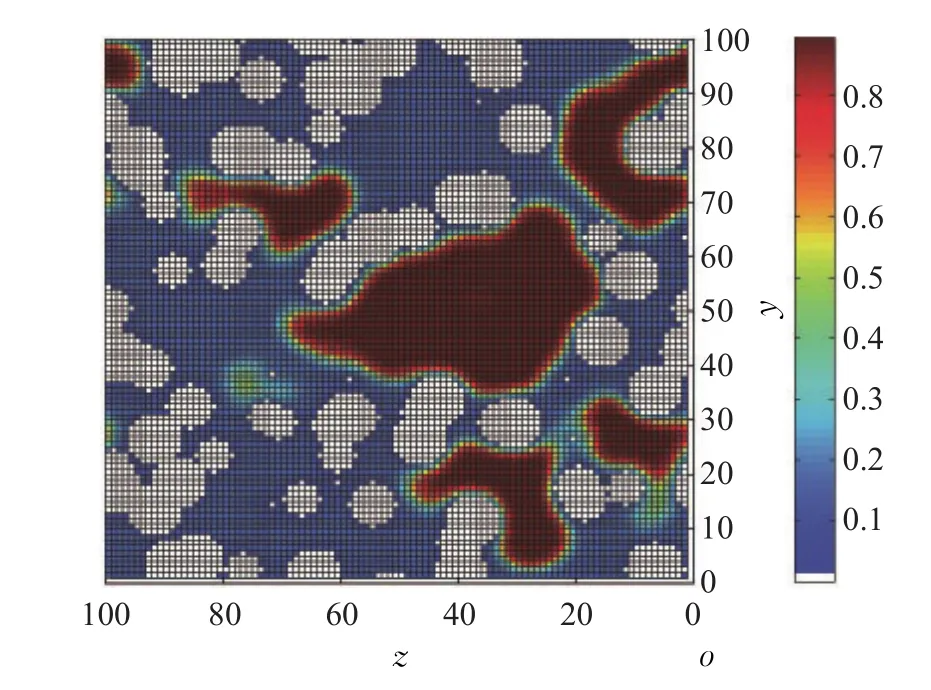
图3 计算机模拟多孔材料格点模型气液相变达到热力学近平衡时在x=0截面上的密度分布
尽管使用原始的建模方法与DCNNs建模方法能够得到相同的物理结果,但是两种方法的运行时间差异巨大。将程序在初始化和迭代过程中占用的运行时间进行比较,如图4所示。随着格点系统体积的增加,用DCNNs方法进行建模初始化占用的时间是线性增加的,系统遵循热力学规律的迭代计算时间也近似于线性递增,然而用原始的建模方法进行初始化占用的运行时间随着系统的格点总数的二次方急剧增加。

图4 不同规模体系模拟的各步骤的运行时间
当系统体积达到106个格点时,应用原始的建模方法与DCNNs建模方法进行计算机模拟的过程中各步骤占用时间的比例,如图5所示。
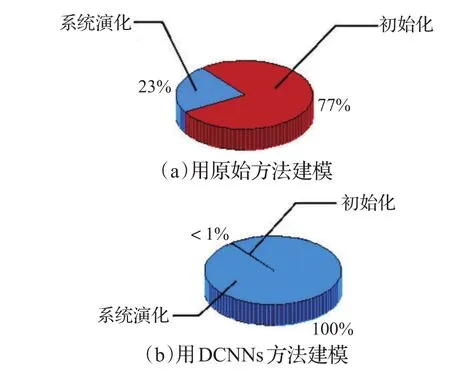
图5 N=106的体系在计算机模拟过程中运行时间的组成
不难发现,随着体系规模的增大,若采用原始建模方法则初始化步骤会占据大部分的运行时间。加之系统演化过程可以很方便地并行加速,初始化步骤的运行时间在总运行时间当中占据的比例有可能会更大。因而对于采用原始方法建模的大规模PMLM系统,初始化步骤严重拖累了整个计算机模拟过程的运行时间,成为用计算机模拟大规模PMLM系统的技术瓶颈。应用DCNNs方法进行建模则只需占用几乎可以忽略不计的运行时间来完成初始化,为更大规模PMLM系统的计算机模拟创造了条件。
4 结束语
本文主要研究了一种适用于PMLM系统进行计算机建模的优化方法。将分治思想与近邻搜索策略相结合,提出的基于分治策略的近邻搜索方法能将计算机建模PMLM系统的时间复杂度由O(N2)降低至O(N)。对PMLM系统气液相变过程的计算机模拟,验证了该方法在不影响物理结果的前提下的高效性。本文提出的优化方法突破了计算机模拟大规模PMLM系统的一个技术瓶颈。
参考文献:
[1]Cormen T H,Leiserson C E,Rivest R L,et al.算法导论:Introduction to algorithms[M].殷建平,徐云,王刚,等译.3版.北京:机械工业出版社,2013:16-17.
[2]王宝文,阎俊梅,刘文远,等.基于分治法的高维大数据集模糊聚类算法[J].计算机工程,2007,33(24):60-62.
7月中旬,我们形成了10个文件,经浦东开发领导小组、市政府常务会、市委常委会和市人大常委会相继审议通过。
[3]李田来,刘方爱,王新华.基于分治策略的改进人工蜂群算法[J].控制与决策,2015,30(2):316-320.
[4]余杰,吕品,郑昌文.Delaunay三角网构建方法比较研究[J].中国图象图形学报,2010,15(8):1158-1167.
[5]Cignonit P,Montanit C,Scopigno R.DeWall:A fast divide and conquer delaunay triangulation algorithm in Ed[J].Computer-Aided Design,1998,30(5):333-341.
[6]Gansterer W N,Ward R C,Muller R P.An extension of the divide-and-conquer method for a cla-ss of symmetric block-tridiagonaleigenproblems[J].ACMTransactions on Mathematical Software,2002,28(1):45-58.
[7]魏立峰,李晓梅.求解对称带状广义特征值问题的扩展分治算法[J].计算机研究与发展,2004,41(5):861-867.
[8]王攀,万君康,冯珊,等.一类基于分治原理的多种群协同进化算法[J].系统工程与电子技术,2004,26(11):1687-1690.
[9]Brennan J K,Dong W.Phase transition of one-component fluids absorbed in random porous media:Monte Carlo simulations[J].The Journal of Chemical Physics,2002,116(20):8948-8958.
[11]马强,陈振乾.分形多孔材料双尺度孔隙内气体脱附扩散过程数值模拟[J].东南大学学报:自然科学版,2015,45(4):728-733.
[12]刘高洁,郭照立,施保昌.多孔介质中流体流动及扩散的耦合格子 Boltzmann 模型[J].物理学报,2016,65(1):282-290.
[13]马强,陈俊,陈振乾.分形多孔介质传热传质过程的格子Boltzmann模拟[J].化工学报,2014,65(S1):180-187.
[14]崔静洁,何文,廖世军,等.多孔材料的孔结构表征及其分析[J].材料导报,2009,23(7):82-86.
[15]Hughes A P,Thiele U,Archer A J.An introduction to inhomogeneousliquids,densityfunctionaltheory,and the wetting transition[J].American Journal of Physics,2014,82:1119-1129.
[16]Dickey J M,Paskin A.Computer simulation of the lattice dynamics of solids[J].Physical Review,1969,188(3):1407-1418.
[17]祝继华,尹俊,邗汶锌,等.面向低维点集配准的高效最近邻搜索法[J].模式识别与人工智能,2014,27(12):1071-1077.
[18]谭骏祥,李少达,杨容浩.迭代最近点匹配算法的树结构k近邻搜索比较研究[J].测绘科学,2014,39(4):152-155.
[19]卫炜,张丽艳,周来水.一种快速搜索海量数据集K-近邻空间球算法[J].航空学报,2006,27(5):944-948.
[20]肇莹,刘红星,王仲宇,等.最近邻搜索用于分类问题的一种改进[J].南京大学学报:自然科学版,2009,45(4):455-462.
[21]Beckmann N,Krigel H P,Schneider R,et al.The R*-tree:An efficient and robust access method for points and rectangles[C]//Hector G M,Jagadish H V.Proceedings of the 1990 ACM SIGMOD Conference on Management of Data.New York:ACM,1990:322-331.

