预应力UHPC梁弯曲性能分析与合理设计

李立峰，范　昕，石雄伟，王连华(1. 湖南大学土木工程学院，湖南长沙　410082； 2. 湖南大学风工程与桥梁工程湖南省重点实验室，湖南长沙　410082； . 西安公路研究院，陕西西安　710065)

0　引　言

超高性能混凝土(UHPC)是一种新型纤维增强水泥基复合材料，与普通混凝土相比，UHPC不仅具有超高抗压强度，而且其弹性模量、抗拉强度更高，徐变系数更小，耐久性好[1]。与同等跨径的高强混凝土构件相比，UHPC构件抗弯承载力要大得多，同时具有良好的变形性能和开裂性能[2-3]，因而具有更好的跨越能力，应用前景广泛。目前，UHPC在桥梁工程领域已经得到了迅速发展。全世界范围内已建成的UHPC桥梁超过100座[4-7]，尤以美、日、法、马来西亚等国应用较多，但中国关于预应力UHPC结构的应用尚处于起步阶段，其中采用全预制或预制拼装施工的简支梁桥占绝大部分，根据跨径不同分别采用T形、π形、U形和箱形等不同截面，梁体内需要布置大量的预应力筋。影响预应力UHPC梁弯曲性能的因素有很多，为了探究其设计理论，国内外学者进行了一系列试验研究。Yoo等[8]研究了不同钢纤维含量及配置不同几何形状钢纤维的UHPC梁极限承载力。杨剑[9]研究了预应力、张拉应力对预应力UHPC梁弯曲性能的影响。徐海宾等[10]对不同配筋率下预应力UHPC梁的弯曲性能进行了研究。

现阶段针对预应力UHPC梁结构的弯曲性能和合理设计方法的研究并不多。为了更好地推动UHPC在桥梁结构中的应用，本文结合一片大比例预应力UHPC-T形梁，并进行弯曲试验，对UHPC梁的弯曲性能进行研究，并结合空间实体有限元进行细致深入的仿真分析；在仿真模型得到验证的基础上，系统研究截面高跨比、截面预应力配筋率、张拉应力、UHPC受压和受拉本构参数等对结构性能的影响；在获得大量分析结果的基础上，探讨预应力UHPC梁的合理设计方法。

1　试验概况

本文主要研究预应力UHPC梁的弯曲力学性能，为此设计了一片大比例预应力UHPC-T形梁，并进行弯曲试验(图1)。试验梁全长10 m，计算跨径9.8 m，梁高600 mm，顶板宽600 mm，下缘宽300 mm，腹板厚70 mm，其他截面尺寸和钢筋布置如图2所示。试验梁下缘布置2束规格为4φS15.2的1860级体内有黏结预应力钢绞线，直线布置，预应力筋形心距截面下缘65 mm；截面上缘和下缘分别布置5根和8根纵向钢筋，直径为12 mm，规格为HRB335；腹板内配置单肢抗剪钢筋，直径为12 mm，间距为100 mm，其他构造钢筋的直径均为8 mm。

图1　加载示意(单位：cm)Fig.1　Schematic Diagram of Loading (Unit:cm)

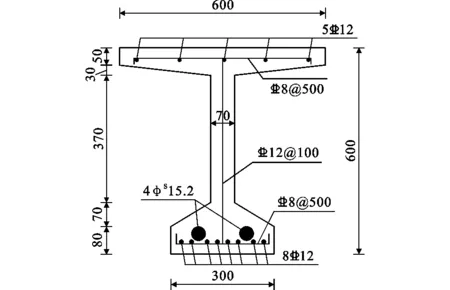
图2　试验梁截面尺寸和纵向钢筋布置(单位：mm)Fig.2　Cross Section Dimension and Longitudinal Reinforcement Arrangement of Test Girder (Unit:mm)

试验梁浇筑后，在室温下常规养护48 h脱模，随即在高温(90 ℃±2 ℃)下蒸汽养护3 d。在室温下存放28 d后进行预应力筋张拉及预应力孔道灌浆，之后进行加载试验。试验梁所用UHPC材料基体配合比见表1，钢纤维体积掺量为2%。同期制作了测试UHPC材料基本力学性能的试块，同条件养护，用于测试UHPC的抗压强度、弹性模量和抗折强度，其基本力学性能测试结果如表2所示。

表1　UHPC基体配合比Tab.1　Composition Ratio of UHPC Matrix

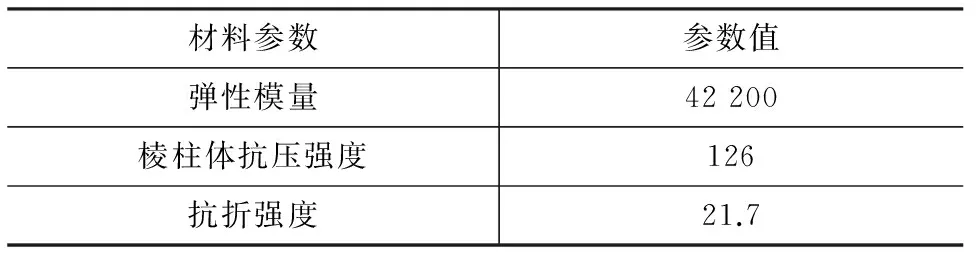
表2　UHPC材料参数Tab.2　Material Parameters of UHPC　MPa

试验梁采用四点弯曲单调分级加载，纯弯段长1.2 m，试验初期按力控制加载，在临近试验破坏阶段，采用位移控制加载。试验过程中对预应力、试验荷载、竖向位移、纵向应变、裂缝等进行测试。

2　预应力UHPC梁有限元分析

2.1　模型建立

2.1.1有限元模型

采用ABAQUS建立非线性有限元分析模型，其中UHPC和支座垫块采用八节点减缩积分单元(C3D8R)模拟，模型网格尺寸为5 cm×5 cm，支座垫块利用绑定约束(tie)与主梁实体连接；普通钢筋和预应力筋采用三维两节点线性杆单元(T3D2)模拟，采用嵌入约束(embedded)将钢筋骨架与UHPC实体进行连接。试验梁有限元模型如图3所示。

图3　试验梁有限元模型及钢筋骨架Fig.3　Finite Element Model and Reinforcement Frame of Test Beam

在非线性有限元模型中，普通钢筋和预应力筋的本构关系均采用理想弹塑性模型，普通钢筋屈服强度为335 MPa，预应力筋极限强度为1 860 MPa；采用降温法模拟预应力的施加。

2.1.2UHPC的CDP模型参数确定

根据已有研究成果[11-12]，ABAQUS提供的混凝土损伤塑性CDP模型能很好地模拟混凝土构件受力变形性能，该模型假定混凝土拉压塑性各向同性，可通过受拉软化来宏观模拟受拉微裂纹的形成，通过受压应力硬化及下降段的应变软化来模拟混凝土的受压塑性。有限元分析需将UHPC的本构关系转换为CDP模型。

(1)UHPC受压应力-应变关系

UHPC的受压应力-应变曲线采用文献[13]提出的公式，即

(1)

式中：σ为应力；fc为UHPC抗压强度；x=ε/ε0，ε为应变，ε0为峰值点对应的应变；a为UHPC受压初始切线模量和峰值割线模量的比值；b为试验拟合参数，取b=2.41。

(2)UHPC受拉应力-应变关系

UHPC的受拉应力-应变曲线采用文献[14]提出的两阶段拉伸本构模型，如图4所示，其中，ft为UHPC单轴抗拉强度，fp=2-pft，p为试验拟合参数，wp为应力降至2-pft时的裂缝宽度，wpc为应力软化起始点的裂缝宽度。

图4　UHPC受拉两阶段本构模型Fig.4　Two-stage Tensile Constitutive Model of UHPC

应力软化阶段采用应力-裂缝宽度关系，如式(2)所示

(2)

根据法国规范建议[15]，按式(3)将应力-裂缝宽度关系转化为应力-应变关系，即

(3)

式中：Et为UHPC受拉初始弹性模量；lc为截面特征长度，与截面形式有关，对于矩形截面和T形截面，取lc=2/3h，h为截面高度。

联立式(2),(3)，同时使σ(εpc)=ft，有

(4)

式中：εpc为应力软化起始点等效应变。

根据文献试验[14]结果，取wp=1.0 mm，p=0.95，εpc=0.002。

UHPC受拉应力-应变曲线公式为

(5)

式中：参考文献[16]，取ft=7.2 MPa；εt0为UHPC受拉线弹性极限应变。

(3)CDP材料模型参数设置

CDP材料模型定义分为弹性和塑性两部分。弹性参数包括弹性模量Ec和泊松比ν，根据表2材性试验结果，参考文献[15]，取Ec=42 200 MPa，ν=0.2。参考文献[17]，塑性参数的设置如表3所示。为了利于结构计算的收敛，取黏聚系数为0.000 5。

表3　UHPC损伤塑性模型塑性破坏准则参数Tab.3　Plastic Collapse Criteria Parameters for Damage Plastic Model of UHPC

(4)UHPC拉、压塑性参数

对于UHPC的单轴受压应力-应变关系，需人为确定弹性极限点εc,e0及弹性极限强度σc,e0。对于UHPC，其单轴受压比例极限一般在0.7～0.8之间[13,18]，本文取其弹性极限强度σc,e0=0.8fc。参考文献[11]，根据式(1)，(5)，对CDP模型受压塑性和受拉塑性进行定义，同时考虑到本文试验未进行循环加载，故不对UHPC的损伤参数进行定义。UHPC的拉、压塑性参数如表4所示。

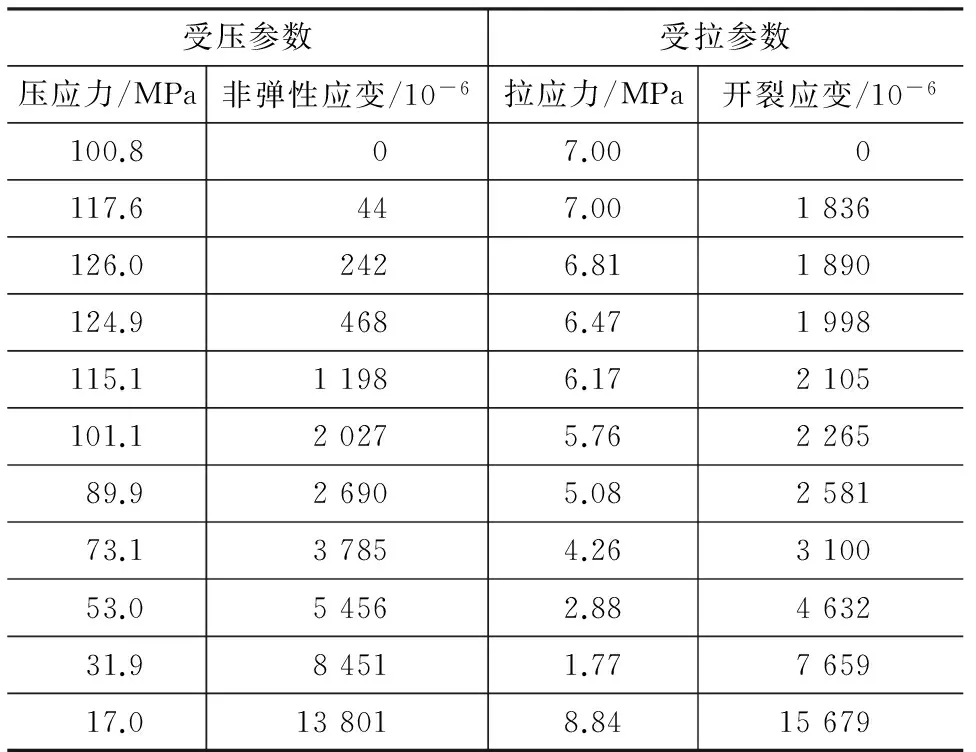
表4　UHPC损伤塑性模型参数Tab.4　UHPC Damage Plastic Model Parameters

2.2　有限元分析结果

为了便于计算收敛，对模型采用位移控制加载，由此进行非线性全过程加载分析。非线性分析收敛性很好，现将主要计算结果与试验结果进行对比，主要包括荷载-位移曲线、极限荷载、结构延性等指标。

2.2.1荷载-位移曲线

试验梁荷载-位移曲线试验值与计算值对比结果如图5所示。由图5可以看出，试验曲线与计算曲线几乎完全重合，并能从计算曲线上获取较为明显的特征点，包括开裂点A、普通钢筋屈服点B、预应力筋屈服点C、荷载下降点D。各关键点试验结果与计算结果对比如表5所示，试验照片如图6所示。由表5可以看出，下降段起始点与试验破坏点位置几乎重合，故可利用计算曲线荷载下降起始点位置对模型梁的破坏进行判别。以上说明该有限元分析模型能较好地模拟预应力UHPC梁的弯曲受力全过程。

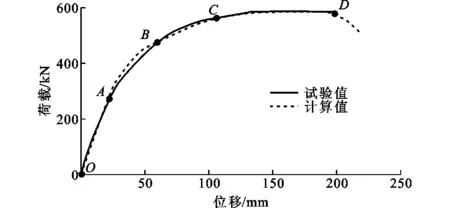
图5　荷载-位移曲线Fig.5　Load-displacement Curves

特征点荷载试验值/kN荷载计算值/kN位移试验值/mm位移计算值/mm开裂点A275.628222.1822.84预应力筋屈服点C563.8562109.00107.00破坏点D584.7583198.00192.00

图6　试验照片Fig.6　Tested Photo

2.2.2破坏模式

对于预应力混凝土结构，依据截面配筋率的大小可将破坏模式划分为适筋梁塑性破坏、超筋梁脆性破坏和少筋梁脆性破坏[19]。

对于预应力UHPC结构，UHPC在开裂之后仍具有一定的抗拉强度，结构不会发生少筋梁脆性破坏。当配筋率过大导致受压区UHPC压碎时预应力筋未屈服，则发生超筋梁脆性破坏。根据受压区混凝土压碎和受拉区预应力筋拉断发生的先后顺序，适筋梁塑性破坏可分为受压区混凝土压碎破坏和受拉预应力筋拉断破坏。

针对以上3种破坏模式，模型计算中可以根据UHPC压碎和预应力筋屈服及拉断发生的先后顺序对模型梁的破坏模式进行判断。参考文献[15]和文献[9]，可取UHPC极限压应变εcu=3 500×10-6，预应力筋极限拉应变εpu=35×10-3。

对于本文试验梁，跨中截面上缘UHPC应变及受拉预应力筋应变与跨中挠度的关系如图7所示，试验梁破坏模式如图8所示。从图7可以看出：预应力筋屈服时，跨中挠度为107 mm，对应图5中平直段起始点C；上缘UHPC达到极限压应变时，跨中挠度为192 mm，对应图5中平直段终止点D。直到计算终止，预应力筋尚未达到极限拉应变。说明模型梁预应力屈服后，上缘UHPC压碎先于预应力筋拉断发生，表现为UHPC压碎塑性破坏，与试验梁破坏模式一致。

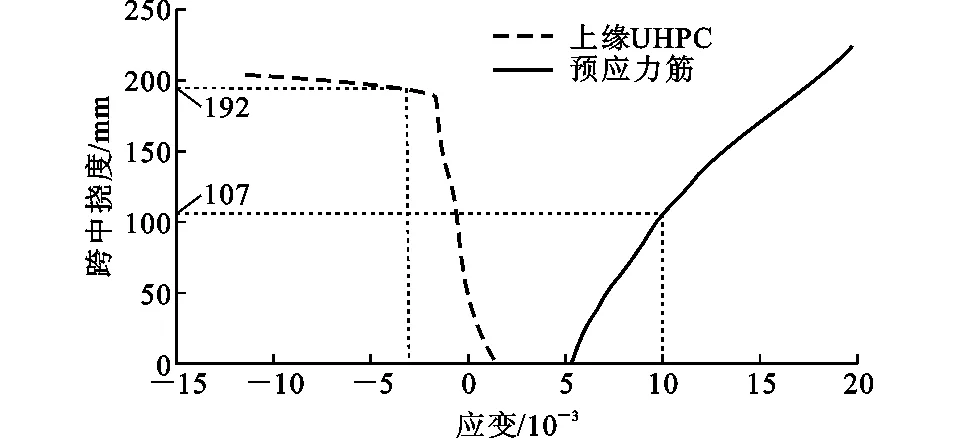
图7　应变与挠度关系曲线Fig.7　Strain-deflection Relation Curves

图8　试验梁破坏模式Fig.8　Failure Mode of Test Beam

2.2.3裂缝分布

图9　主应变云图Fig.9　Nephogram of Principle Strain

图10　实测裂缝分布Fig.10　Distribution of Measured Cracks

将模型主应变云图(图9)与实测裂缝分布(图10)对比可以看出，模型计算的最大主应变分布云图与实测裂缝分布规律相似。虽然CDP模型无法模拟混凝土的开裂，但可通过模型主应变云图对试验梁裂缝分布进行判断。

2.2.4应变结果

跨中截面上、下缘荷载-应变曲线对比结果如图11所示。由图11可以看出，下缘荷载-应变关系曲线在线弹性段能几乎完全重合，当荷载超过300 kN后二者逐渐产生偏差，特别是当荷载超过440 kN后二者完全偏离，可能原因是试验中应变片跨越裂缝工作，应变集中，实测应变值较大。跨中截面上缘荷载-应变关系的试验值和计算值基本吻合。

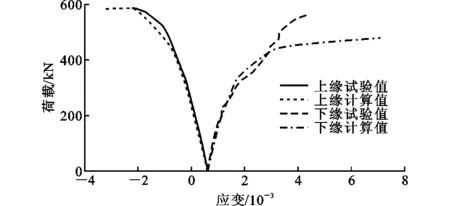
图11　跨中截面上、下缘荷载-应变关系Fig.11　Load-strain Relationships of Upper and Lower Edges of Mid-span Cross Section

3　参数分析

以上分析验证了本文所建立有限元分析模型的正确性和适用性，以此非线性有限元分析模型为基础，进一步研究有限元模型各参数(包括预应力筋数量、张拉应力、UHPC抗压和抗拉性能等)对结构受力性能的影响，为预应力UHPC梁的合理设计提供依据。

3.1　预应力筋数量

保持模型梁参数不变，仅改变受拉区预应力筋面积，分析分别布置6，8，10，12根预应力钢绞线时预应力UHPC梁的抗弯性能，主要包括极限承载力和构件延性大小，预应力筋数量对梁抗弯性能的影响如图12所示。将这些结果与配置8根预应力筋的模型梁结果相比，得到极限承载力和延性指标[20]与预应力筋数量的关系，如图13所示。

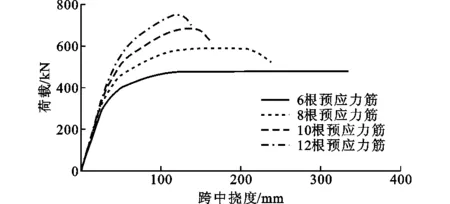
图12　预应力筋数量对梁抗弯性能的影响Fig.12　Influence of Number of Prestressed Tendons on Flexural Performance of Beam

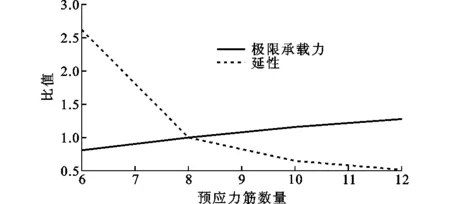
图13　极限承载力和延性随预应力筋数量的变化Fig.13　Changes of Ultimate Bearing Capacity and Ductility with Number of Prestressed Tendons

从图13可以看出：增加预应力筋数量能有效提高构件的极限承载力，且二者呈近似线性关系；提高预应力筋数量会使构件的延性降低，当受拉区配置12根预应力筋时，其荷载-位移曲线几乎不存在平直段。另外，分析截面应变可以看出：当上缘UHPC达到εcu时，预应力筋应力仅为1 720 MPa，说明UHPC压碎先于预应力筋屈服，属于脆性破坏，延性指标也仅为配置8根预应力筋模型梁的0.5倍左右。虽然提高配筋率能明显提高构件的极限承载力，但过高的配筋率会使结构发生脆性破坏。

3.2　张拉应力

保持受拉区预应力筋数量为8根，分析张拉应力分别为800，1 000，1 200 MPa三种情况下结构的抗弯性能，如图14所示。由图14可以看出：增加张拉应力能使模型梁的荷载-位移曲线更加饱满，使模型梁更快进入预应力筋屈服阶段，平直段更长，且极限位移也有所提高，延性更好，但极限承载力并没有提高。因此，增加预应力筋张拉应力大小提高了模型梁受拉边缘的压应力储备，明显提高预应力UHPC构件的抗裂性能。

图14　张拉应力对抗弯性能影响Fig.14　Influence of Tension Stress on Flexural Performance

3.3　抗拉性能

保持模型梁其他参数不变，分析UHPC抗拉强度分别为6，7，8，9 MPa时对结构抗弯性能的影响，如图15所示。由图15可以看出：改变抗拉强度对结构弹性阶段受力没有影响；提高抗拉强度使模型梁开裂阶段构件的刚度有所提升，能略微增强构件的极限承载力；提高抗拉强度能有效提高结构的极限位移和延性。

图15　抗拉强度对抗弯性能影响Fig.15　Influence of Tensile Strength on Flexural Performance

钢纤维含量、几何形状以及构件的浇筑方式等都对UHPC的抗拉性能有较大影响[8，21-22]。因此，应通过优化UHPC中钢纤维的配置和提高构件施工管理水平来提高UHPC的抗拉性能，保证构件延性性能。

3.4　抗压性能

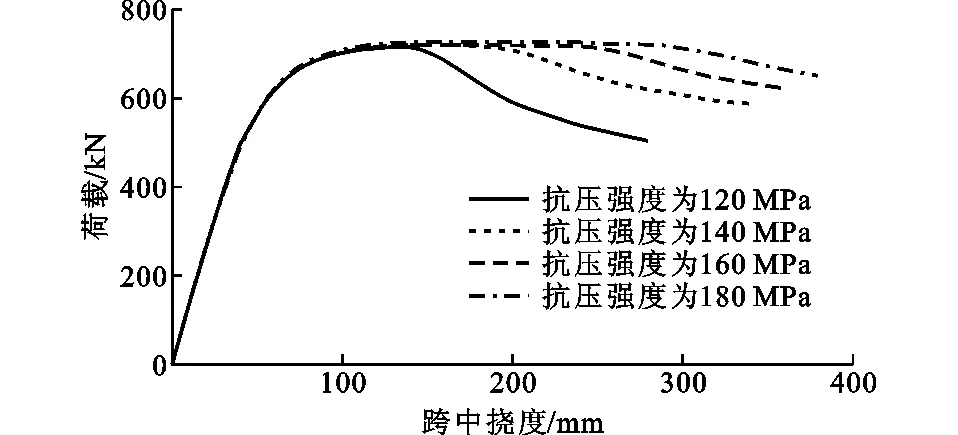
图16　抗压强度对抗压性能影响Fig.16　Influence of Compressive Strength on Compressive Performance

设置模型梁受拉区布置10根预应力筋，张拉应力为1 200 MPa。对UHPC抗压强度进行分析，取抗压强度为120，140，160，180 MPa，对应峰值应变分别为0.003，0.003 5，0.004，0.004 5，分析结果如图16所示。由图16可以看出：UHPC抗压强度的改变对结构弹性阶段和开裂阶段的受力性能以及极限承载力影响不大；保持UHPC受压初始弹性模量不变，提高抗压强度时对应峰值应变也会增加，这样可使上缘受压混凝土的压碎发生在预应力筋屈服之后，使模型梁表现出更好的延性。

4　预应力UHPC梁合理设计

根据参数分析结果，并结合已有桥梁调查结果，对预应力UHPC梁的高跨比、相对界限受压区高度及配筋率限值进行探讨计算，并对其合理设计方法进行探究。

4.1　高跨比

高跨比直接影响结构的的承载能力和刚度。对于预应力UHPC梁，可以通过配置足够的预应力筋以及合理的构造措施，保证结构在高跨比很小的情况下具有足够的承载力，因此，其高跨比较预应力普通混凝土梁要小，但是过小的高跨比会使结构刚度降低，影响结构的变形和使用性能。

对全世界范围内已建的41座预应力UHPC公路桥和人行桥进行调查[4-7]，其高跨比分布情况如图17所示。UHPC公路桥高跨比一般介于1/28～1/16之间，跨径小于40 m时，截面多采用I形、π形和T形梁等开口截面，跨径大于40 m时，截面多采用箱形截面。人行桥高跨比范围较广，高跨比大于1/30时，多采用开口式槽形截面，高跨比小于1/30时，多采用箱形截面。

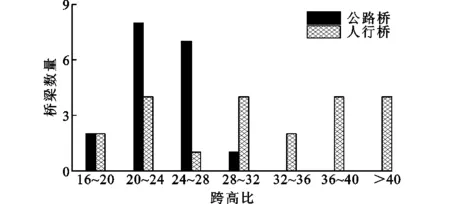
图17　已建UHPC桥梁跨高比分布Fig.17　Distribution of Span-depth Ratios of Existing UHPC Bridges

关于高跨比的合理选择需要更深入的研究，根据对已建UHPC桥梁的调查结果，本文建议预应力UHPC公路桥高跨比应介于1/25～1/18之间。

4.2　相对界限受压区高度

对于预应力混凝土构件来说，相对界限受压区高度ξb不仅取决于钢筋和混凝土的力学性能，还与预应力的大小有关。参考文献[19]，以应力表示相对界限受压区高度，即

(6)

式中：β为等效矩形受压区高度系数，假定UHPC受压区应力分布为三角形，则β=0.66；fpk，Ep分别为预应力钢绞线的抗拉强度和弹性模量；σp0=σpe+αEpσpc,p，σpe为预应力筋的有效预应力，σpc,p为预应力筋重心处混凝土的预压应力，αEp为预应力筋和UHPC的弹性模量比。

根据参数分析结果，在配筋率一定的情况下，应通过提高张拉应力使结构获得更好的延性，因此取σpe=1 300 MPa用于计算。对于本文模型梁，σpc,p=37 MPa，αEp=4.577，代入式(6)，可得相对界限受压区高度ξb=0.307。对于高强混凝土C80，其相对界限受压区高度为0.35，可以看出，预应力UHPC构件的界限受压区高度较高强混凝土C80要小。

4.3　配筋率限值

对于预应力UHPC构件，合理的破坏模式应该为适筋梁塑性破坏，同时UHPC的压碎先于预应力筋的拉断，这样能充分利用UHPC的超高抗压强度，同时结构在破坏后尚有一定的承载能力，不致倒塌。最大配筋率为发生界限破坏时所对应的界限配筋率，最小配筋率为预应力筋断裂同时UHPC压碎所需的配筋率。

对于预应力筋拉断同时UHPC压碎的状态，用预应力筋的极限拉应变εpu替代式(6)中的预应力筋屈服应变，则最小相对高度ξmin为

(7)

由式(7)计算得ξmin=0.075。

考虑UHPC受拉性能，不考虑受压钢筋。对于T形梁，界限配筋率下，中性轴位于腹板内，根据内力平衡条件有

αfcd[bwx+(b′-bw)hf]=fpAp+kftAt

(8)

式中：fcd为UHPC抗压强度；Ap为受拉区预应力筋截面面积；At为受拉区UHPC截面面积；α为等效矩形受压区强度系数，取为0.75；k为等效矩形受拉区强度系数，参考文献[23]，取为0.25；bw为腹板厚度；b′，hf分别为翼缘板厚度和宽度。

最小配筋率下，中性轴位于翼缘内，则

αfcdb′x=fpAp+kftAt

(9)

将界限受压区高度系数代入式(8)，计算得Ap=2 066 mm2，则界限配筋率ρb=5.5%。

将ξmin代入式(9)，计算得最小配筋率ρmin=2.7%。

4.4　合理设计

根据对已有UHPC桥梁的调查结果，建议公路UHPC桥梁高跨比介于1/25～1/18之间。

根据参数分析，为使预应力UHPC梁在获得更高承载力同时保持一定的延性，应适当增加预应力筋配筋率，同时提高预应力筋张拉应力。建议预应力UHPC梁的张拉控制应力σcon可按预应力普通混凝土构件取σcon=0.75fpk。

在确定预应力筋张拉应力的情况下，为保证其发生合理的破坏模式，其预应力筋配筋率上、下限值可按第4.3节计算，根据本文试验梁参数，建议其配筋率ρ应满足

2.7%≤ρ≤5.5%

(10)

在配筋率不变的情况下，提高UHPC的抗压强度和抗拉强度均能有效提高结构的延性，因此，使用性能更优的材料或通过提高施工管理水平，保证构件材料的性能，进而提高并保证结构表现良好的受力性能。

5　结语

(1)基于混凝土损伤塑性(CDP)的有限元模型能较好模拟预应力UHPC梁的弯曲受力性能。

(2)增加配筋率能有效提高结构的极限承载力，但是结构延性会降低；提高预应力筋张拉应力是提高结构延性的有效方法，同时能有效提高结构的抗裂性能；提高UHPC的抗压强度和抗拉强度能有效提高结构的延性。

(3)建议预应力UHPC公路桥高跨比介于1/25～1/18。为保证预应力UHPC构件表现出更好的受力性能，可根据本文提出的计算公式对其配筋率范围进行确定。对于本文试验梁，其配筋率应满足2.7%≤ρ≤5.5%。

参考文献：

[1]GRAYBEAL B A.Material Property Characterization of Ultra-high Performance Concrete[R].McLean:Federal Highway Administration,2006.

[2]GRAYBEAL B A.Flexural Behavior of an Ultra High-performance Concrete I-girder[J].Journal of Bridge Engineering,2008,13(6):602-610.

[3]VOO Y L,FOSTER S J,VOO C C.Ultrahigh-performance Concrete Segmental Bridge Technology:Toward Sustainable Bridge Construction[J].Journal of Bridge Engineering,2014,7(4):1-12.

[4]RUSSELL H G,GRAYBEAL B A.Ultra-high Performance Concrete:A State-of-the-art Report for the Bridge Community[R].Washington DC:Federal Highway Administration,2013.

[5]VOO Y V,FOSTER S J,FAIZ M,et al.The Current State of Art of Ultra-high Performance Concrete Bridge Construction in Malaysia[R].Selangor:IEM,2014.

[6]VOO Y L,TADROS M K.Taking Ultra-high-performance Concrete to New Heights the Malaysian Experience[J].Magazine of Concrete Research,2016,10(3):36-39.

[7]UEDA T.The Report of the Super High Quality Cementitious Material[R].Sapporo:Hokkaido Civil Engineering Technical Committee,2014.

[8]YOO D Y,YOON Y S.Structural Performance of Ultra-high-performance Concrete Beams with Different Steel Fibers[J].Engineering Structures,2015,102:409-423.

[9]杨剑.CFRP预应力筋超高性能混凝土梁受力性能研究[D].长沙:湖南大学,2007.

YANG Jian.Flexural Behavior of Ultra-high Performance Concrete Beams Prestressed with CFRP Tendons[D].Changsha:Hunan University,2007.

[10]徐海宾,邓宗才.预应力超高性能钢纤维混凝土梁受弯性能试验研究[J].建筑结构学报,2014,35(12):58-64.

XU Hai-bin,DENG Zong-cai.Experimental Research on Flexural Behavior of Prestressed Ultra-high Performance Steel Fiber Concrete Beams[J].Journal of Building Structures,2014,35(12):58-64.

[11]聂建国,王宇航.ABAQUS中混凝土本构模型用于模拟结构静力行为的比较研究[J].工程力学,2013,30(4):59-67,82.

NIE Jian-guo,WANG Yu-hang.Comparison Study of Constitutive Model of Concrete in ABAQUS for Static Analysis of Structures[J].Engineering Mechanics,2013,30(4):59-67,82.

[12]CHEN L,GRAYBEAL B A.Modeling Structural Performance of Second Generation Ultra-high Performance Concrete Pi-girders[J].Journal of Bridge Engineering,2012,17(4):634-643.

[13]单波.活性粉末混凝土基本力学性能的试验与研究[D].长沙:湖南大学,2002.

SHAN Bo.Research and Test on the Basic Mechanical Behavior of Reactive Powder Concrete[D].Changsha:Hunan University,2002.

[14]张哲,邵旭东,李文光,等.超高性能混凝土轴拉性能试验[J].中国公路学报,2015,28(8):50-58.

ZHANG Zhe,SHAO Xu-dong,LI Wen-guang,et al.Axial Tensile Behavior Test of Ultra High Performance Concrete[J].China Journal of Highway and Transport,2015,28(8):50-58.

[15]AFGC/SETRA 2013,Ultra High Performance Fibre Reinforced Concretes[S].

[16]张哲,邵旭东,朱平,等.基于超高性能混凝土弯曲拉伸特性的二次倒推分析法[J].土木工程学报,2016,49(2):77-86.

ZHANG Zhe,SHAO Xu-dong,ZHU Ping,et al.Twice Inverse Analysis Method Based on Four-point Bending Test Results for UHPC Tensile Behavior Characterization[J].China Civil Engineering Journal,2016,49(2):77-86.

[17]李昊煜.RPC材料的塑性损伤本构模型参数识别及有限元验证[D].北京:北京交通大学,2009.

LI Hao-yu.Parametric Identification for Reactive Powder Concrete Damage Plasticity Constitutive Model and FEM Verification[D].Beijing:Beijing Jiaotong University,2009.

[18]GRAYBEAL B A.Compressive Behavior of Ultra-high-performance Fiber-reinforced Concrete[J].ACI Materials Journal,2007,104(2):146-152.

[19]张树仁,黄侨.结构设计原理[M].2版.北京:人民交通出版社,2010.

ZHANG Shu-ren,HUANG Qiao.Principle of Structure Design[M].2nd ed.Beijing:China Communications Press,2010.

[20]JEONG S M,NAAMAN A E.Ductility of Concrete Beams Prestressed with FRP Tendons[C]//ASCE.Restructuring:America and Beyond.Reston:ASCE,1995:1466-1469.

[21]YANG I H,JOH C,KIM B S.Structural Behavior of Ultra High Performance Concrete Beams Subjected to Bending[J].Engineering Structures,2010,32:3478-3487.

[22]ALI A.Behavior of Prestressed Ultra-high Performance Concrete I-beams Subjected to Shear and Flexure[D].Ottawa:University of Ottawa,2013.

[23]郑文忠,李莉,卢姗姗.钢筋活性粉末混凝土简支梁正截面受力性能试验研究[J].建筑结构学报,2011,32(6):125-134.

ZHENG Wen-zhong,LI Li,LU Shan-shan.Experimental Research on Mechanical Performance of Normal Section of Reinforced Reactive Powder Concrete Beam[J].Journal of Building Structures,2011,32(6):125-134.