粒子群算法用于局部放电小波阈值去噪

李蓝青，赵刚(上海交通大学 电气工程系 电力传输与功率变换控制教育部重点实验室，上海　200240)

0　引　言

在局放检测技术中，脉冲电流法[1]、特高频法[2-3]等方法得到了广泛的关注和研究。为了提高局放检测的灵敏度和精度，许多抗干扰电路[4]、数字降噪法[5-6]以及综合抗干扰方法[7-9]得到了应用。

局放测量中的干扰按波形特征可分为连续周期性干扰、脉冲型干扰和白噪声[10]。前两种干扰可通过两通道局放测量方法中同步实时采集来去除，但前提是摆脱信号中白噪声的影响。小波阈值去噪可以有效去除局放信号中的白噪声，其理论基础是统计估计：认为真实信号对应的小波系数少但是绝对值大，而白噪声对应的小波系数多但绝对值小。故而采取适当的阈值来去除绝对值较小的系数并保留或收缩绝对值较大的系数，再依此系数重构信号，达到去除白噪声的目的。Donoho提出了软阈值法和硬阈值法[11]，并给出了一种计算阈值的方法。

近年来，许多研究优化和改进了传统小波阈值方法，包括改进阈值函数[12]，结合其他分析方法[13]，引入优化算法[14]等，并在图像处理等领域取得了很大进展[15-16]。

本文提出了一种基于粒子群算法的小波阈值去噪方法，使用该算法确定最优阈值来达到局放信号去噪的目的。

1　小波阈值去噪法

设X=[x1,x2,…,xN]为含噪信号的观测值时间序列，对任一xi有：

xi=si+ei,i=1,2,…,N

(1)

(2)

均方误差的确是去噪的目标，但是，在实际信号去噪中，原始信号一般是无法预知的，即s未知，所以均方误差并不能作为阈值选取的准则。本文采用广义交叉验证(Generalized Cross Validation)[17]作为标准来选取阈值，并会在第3.1部分进行介绍。

2　粒子群算法基本原理

2.1　粒子群算法

粒子群算法，又称粒子群优化算法或鸟群觅食算法(Particle Swarm Optimization)，是由Kennedy和Eberhart等[18]开发的一种新的进化算法。它在一定的搜索域内从随机解出发，以适应度函数来评价解的优劣，通过迭代来寻求最优解。每个粒子以其个体以及整个粒子群体当前搜索到的最优值来不断修正自己的搜索方向及速度以求找到全局最优。粒子群算法编码简单，对软硬件要求不高，具有实现容易、收敛快、精度高等优点。

2.2　算法编码

设在m维搜索域内有n个粒子，对第i个粒子(i=1,2,…,n),以pi和vi来表示其位置矢量和速度矢量：

pi=[pi1,pi2,…,pim]

(3)

vi=[vi1,vi2,…,vim]

(4)

适应度函数f根据具体问题设置, 第i个粒子的适应度值：

Fitnessi=f(pi)

(5)

第i个粒子当前搜索到的最优适应度值对应的位置：

pbesti=[pbesti1,pbesti2,…,pbestim]

(6)

粒子群体当前搜索到的最优适应度值对应的粒子位置：

gbest=[gbest1,gbest2,…,gbestm]

(7)

每个粒子通过pbesti和gbest来更新自己的速度和位置：

(8)

(9)

式中：k为迭代次数；d为维数(d=1,2,…,m)；w为惯性权重，当w较大时，全局搜索能力强，当w较小时，局部搜索能力强，一般设置w随迭代次数增加由0.9递减至0.4；c1,c2为认知系数和社会系数，通常取c1=c2=2；U为[0,1]均匀分布的随机数。

3　基于粒子群算法的最优阈值估计

3.1　适应度函数

交叉验证主要用于建模应用[19]和机器学习[20]当中。在没有先验数据的前提下，将样本分成若干份，留一份作为验证，其余用来建模，并循环这一流程以求取最优的模型。作为交叉验证对一般模型的推广，广义交叉验证可以作为均方误差的一个近似估计，根据其准则可定义如下函数作为适应度函数：

(10)

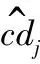
3.2　算法步骤

使用粒子群算法进行寻优时，首先要对问题的解进行编码，构成算法中粒子的位置矢量。再确定适应度函数，计算出每个粒子的适应度值。之后在搜索域内通过进化函数进行迭代，获得最优解。

第一步，以小波分解层数m作为搜索域的维数，以各层阈值作为粒子在每一维中的位置。初始阈值为搜索域内的随机值。

第三步，按照式(8)、式(9)更新粒子的速度和位置，并重复第二步的计算，继续更新个体最优和群体最优。

第四步，重复第三步的更新直至两次迭代之间的最优值之差小于一给定极小值或达到最大迭代次数。

4　仿真实验分析

这一部分将对人工模拟加噪信号和典型局放脉冲仿真信号进行去噪处理和误差分析，以对本文提出的方法进行检验。人工模拟信号使用MATLAB提供的两种模拟加噪信号noisbloc和noisdopp，局放脉冲信号采用文献[16]124中两种局放检测仪可能采集到的脉冲信号，即指数衰减型脉冲信号和震荡衰减型脉冲信号。

4.1　去噪信号误差的数学定义

误差的度量将采用第1部分中提到的均方误差(MSE)式(2)以及幅值误差(Magnitude Error,ME)这两种指标：

(11)

式中：N为信号的总长度。MSE和ME越小表明去噪效果越好。

4.2　几种仿真信号的去噪分析

4.2.1人工模拟加噪信号的去噪分析

使用MATLAB提供的两个信号noisbloc和noisdopp(即blocks信号加噪和Doppler信号加噪)做去噪处理。使用db8作为小波基，分解层数为6层。分别采用Donoho标准软阈值法(Soft Thresholding Method,STM)和本文提出的粒子群阈值法(PSO Thresholding Method,PSOTM)进行去噪，定量分析如表1所示。

表1　人工模拟加噪信号去噪结果

对于noisbloc信号，PSOTM的MSE比STM的降低了15%，ME降低了10%。对于noisdopp信号，MSE降低了25%，ME降低了11%。从结果中可以看出，粒子群阈值法对于两种信号的去噪效果明显优于标准软阈值法。

4.2.2局放仿真信号的去噪分析

局放信号是短时脉冲信号，式(12)、式(13)定义了指数衰减型和震荡衰减型两种脉冲信号：

S1(t)=A×(e-a1t-e-a2t)

(12)

S2(t)=A×(e-a1t×cos(2πft)-e-a2t)

(13)

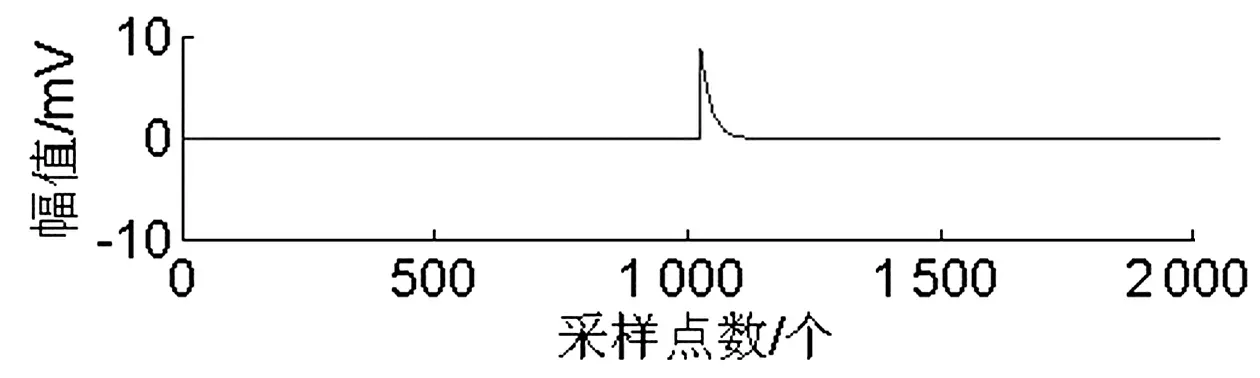
图1　仿真局放信号S1波形

图2　仿真局放信号S2波形

式中：A为信号幅值;a1,a2为时间常数;f为震荡频率。两种信号的波形如图1和图2所示。

分子标记技术能从分子水平上反映生物个体间差异，具有较高的多态性与重演性，SSR分子标记技术用于作物纯度鉴定已是成熟的技术，能以较小的成本、较短的时间准确、稳定地鉴定品种的纯度。该研究从均匀分布在水稻染色体上的48对SSR引物中筛选到18对用于鑫两优212杂交种纯度鉴定，选用其中的3对引物可以快速、较为准确地鉴定出鑫两优212纯度。从筛选的18对引物中筛选特异性较强的引物组合对鑫两优212杂交种进行鉴定，能够减少很多的工作量和成本，且效果更好，可靠性更高。

图3　S1添加三种噪声后的波形

图4　S2添加三种噪声后的波形

仿真局放信号的长度均为2 048点，在进行去噪分析时，为了验证算法的有效性和普适性，对仿真局放信号S1、S2添加不同种类噪声进行了实验分析。第一种是在上述信号的基础上添加均值为0信噪比为1的高斯白噪声得到S1n1、S2n1;第二种是添加概率分布为瑞利分布，均值为0，b=15的瑞利噪声得到S1n2、S2n2;第三种是添加均值为0幅值为3.5的均匀噪声得到S1n3、S2n3。染噪信号如图3和图4所示。

图5　S1n1去噪结果

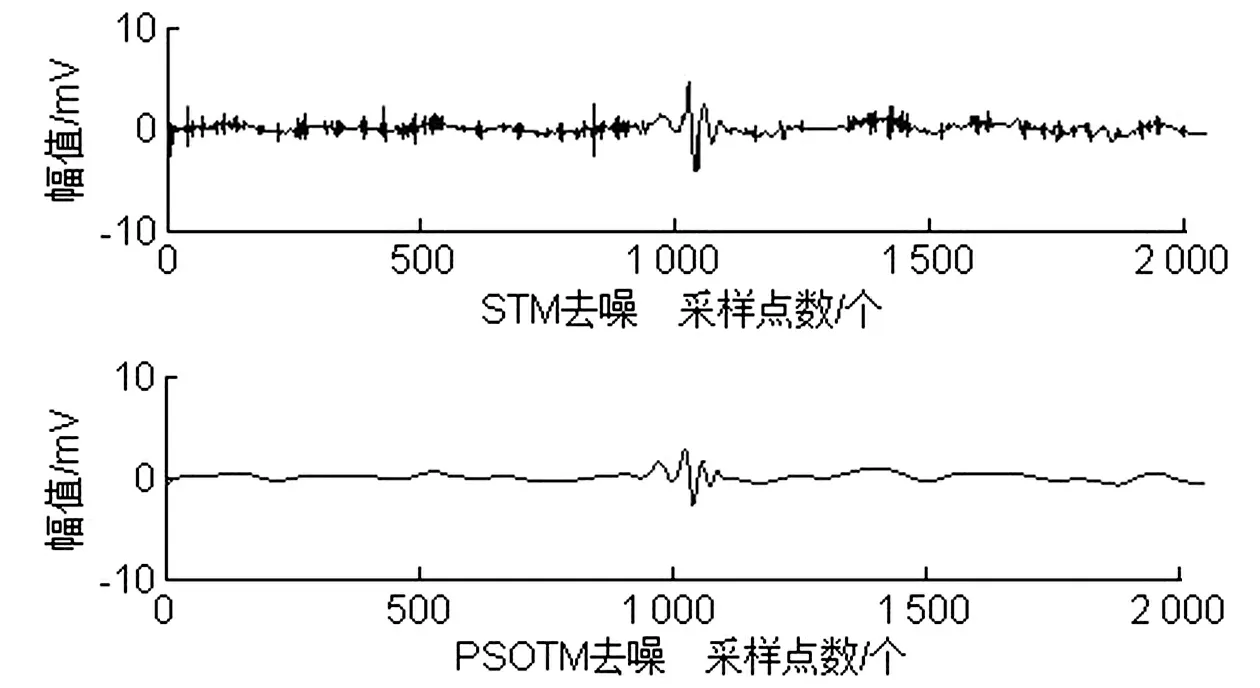
图6　S2n1去噪结果

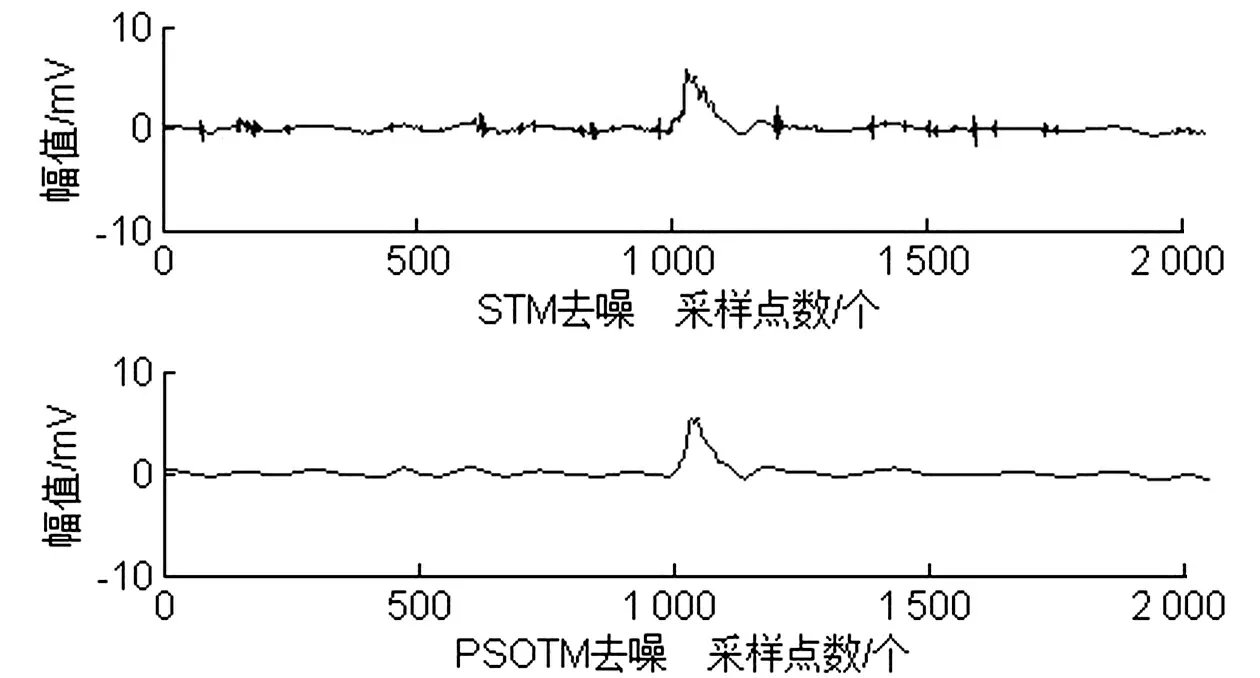
图7　S1n2去噪结果

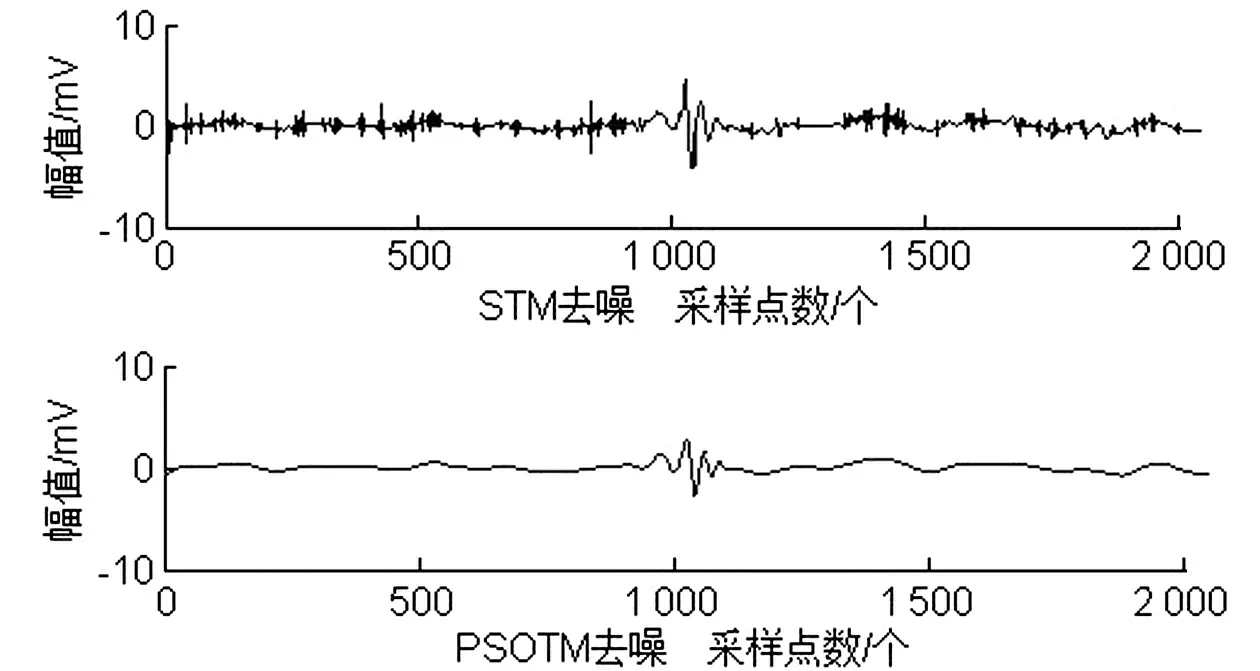
图8　S2n2去噪结果

图9　S1n3去噪结果

对这几个染噪信号做去噪处理，使用db8作为小波基，分解层数为6层。分别采用STM和PSOTM进行去噪，S1n1、S2n1去噪后的波形如图5和图6所示。从图中可以看出PSOTM去噪后曲线平滑没有细小毛刺，即去除了更高频的部分，更好地保留了有效信号。其去噪效果优于STM，滤除的噪声更多，与原始信号的相似程度也更高，MSE指标也能印证这一点。

S1n2、S2n2、S1n3、S2n3信号去噪结果如图7～图10所示。从图中可以看出，STM和PSOTM对添加了瑞利噪声的信号去噪效果都较好，但对于均匀噪声，STM的去噪结果几乎无法分辨局放信号，而PSOTM较STM去噪效果有了很大的提升，也由此证明该方法的有效性。

对几种加噪信号去噪后的定量分析如表2所示。添加高斯白噪声之后，对于仿真局放信号S1，PSOTM的MSE比STM的降低了28%，ME降低了20%；对于仿真局放信号S2，MSE降低了23%，ME降低了28%。从结果中可以看出，粒子群阈值法对于添加了高斯白噪声的两种信号去噪效果都优于标准软阈值法。

添加瑞利噪声之后，对于仿真局放信号S1,S2，PSOTM的去噪结果优于STM，但是效果提升的幅度并不如高斯白噪声大。相反，对于添加均匀噪声的去噪结果，效果提升幅度却十分明显，有50%左右，说明该算法对于均匀噪声的去噪效果更优。

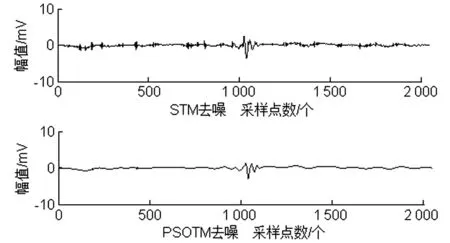
图10　S2n3去噪结果

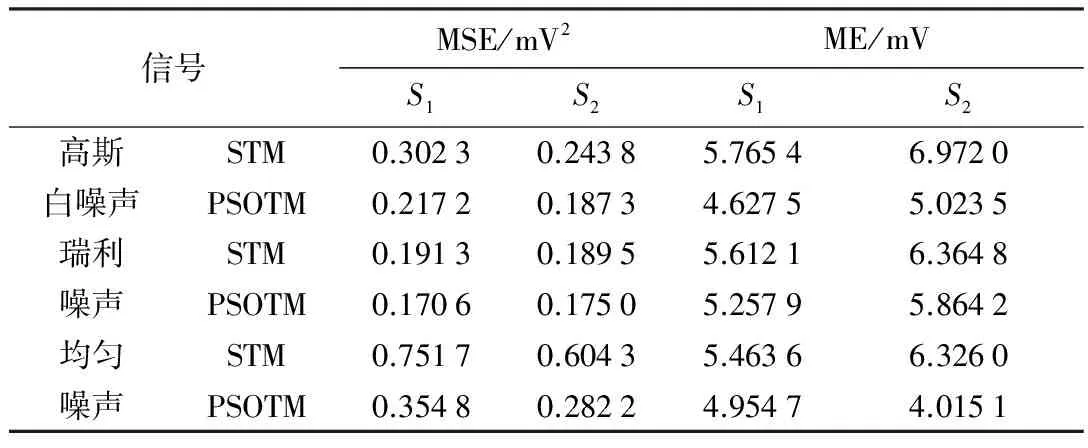
表2　局放仿真信号去噪结果

5　结束语

介绍了小波阈值去噪法的基本原理，提出了一种基于粒子群算法的阈值去噪方法，应用于局放信号去噪。

(1)在标准软阈值法的基础上引入粒子群算法来对阈值的选取进行优化，利用了粒子群算法编码简单、搜索范围广、收敛速度快的优点，达到阈值选优的目的。

(2)使用MATLAB自带的噪声信号来做去噪处理分析证明了所提出的方法具有一定的普适性。使用两个仿真局放信号做去噪处理和定量分析，证明了该方法对于局放信号的去噪有着很好的效果。

参考文献：

[ 1 ] 全国高电压试验技术和绝缘配合标准化技术委员会.GB/T 7354-2003局部放电测量[S].北京:国家质量监督检验检疫总局,2003.

[ 2 ] 杨森,熊俊,郑服利,等. 基于特高频无线智能传感器的局部放电定位法[J]. 电气自动化,2017,39(2):110-112,115.

[ 3 ] 魏翀,熊俊,杨森. GIS局部放电带电检测技术分析与现场应用[J]. 电气自动化,2016,38(2):106-108,114.

[ 4 ] 唐志国,蒋佟佟,刘昌标,等. 高频电流法检测电容器局部放电的抗干扰研究[C]//中国电机工程学会高电压专业委员会2015年学术年会论文集,2015:1-6.

[ 5 ] 王永强,谢军,律方成,等. 基于改进量子粒子群优化稀疏分解的局放信号去噪方法[J].电工技术学报,2015,30(12):320-329.

[ 6 ] 刘红霞,钱勇,姚林朋,等. 基于模糊聚类的XLPE电缆随机脉冲干扰抑制方法研究[J]. 电气自动化,2011,33(2):76-78,81.

[ 7 ] 刘大永,刘秀凤,李付有,等. 局部放电检测抗干扰分析[J].硅谷,2015,14 (4):57-57,38.

[ 8 ] 孙振华,冯金茏,欧阳力,等. 开关柜超声波局放检测抗干扰方法研究[J].湖南电力,2016,36(2):46-49.

[ 9 ] 马振祺,刘克发,温定筠,等. 超高压电缆局放在线监测局放信号提取技术研究及应用[J].电测与仪表,2016,53(18):93-99.

[10] 彭炜文,田慕琴,宋建成,等. 一种基于EEMD和高阶统计量的局部放电白噪声抑制方法[J].高压电器,2016,52(5):54-59,64.

[11] DONOHO D L. De-noising by soft-thresholding[J]. IEEE Transactions on Information Theory, 1995, 41(3):613-627.

[12] 曹京京,胡辽林,赵瑞. 一种改进小波阈值函数的光纤光栅传感信号去噪方法[J]. 传感技术学报,2015,28(4):521-525.

[13] 韩子扬,杜利明,王鑫,等. 一种改进的小波阈值去噪方法[J]. 现代电子技术,2016,39(17):20-22,25.

[14] 李新春,吴秋铜. 基于改进遗传算法的小波阈值语音去噪[J]. 激光杂志,2015,36(1):62-65.

[15] 刘洲峰,徐庆伟,李春雷,等. 小波变换在图像检测中的应用[J]. 电气自动化,2008,30(6):90-91.

[16] 程昌奎,郑永建,庞军,等. 变压器局部放电监测中的最优小波与脉冲鉴别去噪方法研究[J]. 高压电器,2016,52(3):123-128.

[17] CRAVEN P, WAHBA G. Smoothing noisy data with spline functions[J]. Numerische Mathematik, 1975, 24(5):383-393.

[18] KENNEDY J, EBERHART R. Particle swarm optimization[C]// IEEE International Conference on Neural Networks, 1995,Proceedings. IEEE Xplore, 1995:1942-1948.

[19] 任哲,陈怀亮,王连喜,等. 利用交叉验证的小麦LAI反演模型研究[J]. 国土资源遥感,2015,27(4):34-40.

[20] 李洪江,刘栋. 基于交叉验证支持向量机的短期负荷预测[J]. 云南电力技术,2016,44(3):1-3,13.