等效正弦分级变频软启动器的研究

杨宁波，童军(西安科技大学 电气与控制工程学院，陕西 西安　710054)

0　引　言

由于电力电子技术的发展和各种电力电子器件的出现，基于晶闸管调压原理的电机软启动器对于解决启动过程中的问题有很大的贡献。软启动技术有变频器控制的软启动和分级变频软启动，变频器可以最大限度地限制电动机的启动电流，减少电网压降，可实现恒转矩及变转矩启动。但是由于变频器的价格昂贵且使用成本增加和维修比较复杂，所以变频器的使用受到了很大的限制。分级变频的优点将可以很好的弥补变频器的缺陷。1999年Dr. Ginart Antonio(U.S.)提出了分级变频的理论，将工频输入的波进行周波控制，使得某些半波导通，某些半波截止，从而通过增加输出电压的周期来降低频率，也就是说频率的变化是整倍数的。所谓的分级变频软启动就是通过某种控制方法将这些不同的频率进行切换，最后达到工频和额定转速[1-2]。分级变频可以在降低启动电流的同时有效提高异步电机的初始启动转矩。但是，分级变频在实际工程应用中还存在较多的问题，本文将对启动的时候存在的一些问题进行讨论。

1　系统原理介绍

分级变频软启动器主要采用传统软启动器主电路拓扑结构，将工频输入的某些半波导通，某些半波截止，从而增加输出电压的周期以降低频率[3]。下面介绍A相2分频的产生过程，通过控制晶闸管的通断来使得工频在两个周期中有一个正半波导通和一个负半波导通，但是这存在四种不同的组合方式，如图1所示。这四种方式都可以形成的25 Hz的波形，其中频率和幅值相同，相位不同[4]。

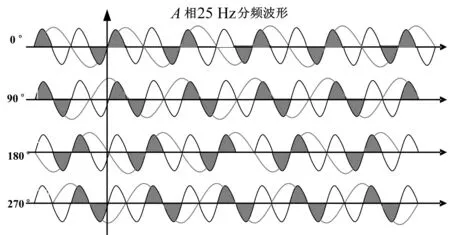
图1　1/2分频电压波形相位示意图

由于三相分级变频不是连续变化的，所以使得电机在启动的时候会出现很多问题，比如分级变频后电源的相序，频段的选择与频段之间的切换和功率因数角校正等。

2　分级变频的相序问题

三相电源提供的频率为工频50 Hz，角速度为ωnet，电压幅值为UL,则三相电压值为：

(1)

经过m分频，新的子频率下的三相电压基波瞬时值为：

(2)

式中：ωnet=mωsub。

假设A相的相位角φA=0，可知：

(3)

(4)

当m=3k+1，即m为4、7、10…时，得到的新的子频率下的三相正序对称电压，此时任意两相的相位差为2π/3；当m=3k-1，即m为2、5、8、11…时，得到的是三相负序对称电压；当m=3k时，得到的新的电压只有零序分量。这些对称的分频中只有偶分频的波形关于时间轴上是不平衡的。

在启动的时候希望所选择的子频率为正序平衡，如13分频和7分频，对于一些不完全平衡的方式，如4分频和3分频以及完全负序对称的2分频需要采用对称分量法来对其进行分解[5]。将正序分量、负序分量和零序分量的标注为“+”、“-”和“0”，运用对称分量法来进行分解，可以得到如下式：

(5)

设变换系数：

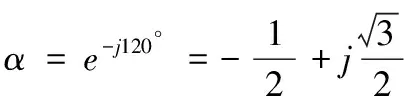
(6)

对式(6)进行计算得：

(7)

通过计算可得，3分频的时候，(0°，260，100°)、(0°，260°，160°)和(0°，200°，100°)满足正序分量最大和负序分量最小的要求。2分频的时候，(0°，210°，60°)、(0°，210°，150°)、(0°，300°，150°)满足正序分量最大和负序分量最小的要求。

3　不同频段的选择与切换

分级变频的初始启动转矩与频率成反比，所以频率越低，启动转矩越大[6]。但是初始频率太低会增大启动时间，而且在启动的时候尽量让正序分量最大和负序分量最小，这样可以最大地启动转矩，满足电机可以满载或者重载启动[7]。本文采用斜坡电压的启动方式对其进行改善。所以选择的分级变频启动方式为13分频→7分频→4分频→3分频→2分频→斜坡电压→50 Hz的过程。

4　触发角控制策略

传统的分级变频软启动常采用固定触发角度的控制策略[8]，这种控制方法得到的电压不是正弦波形，故其谐波含量比较大。本文采用等效正弦控制的方法可以计算出启动过程中各级晶闸管触发角，使得输出电压波形为等效正弦。如图2所示，图为7分频的电压等效正弦波形，其中实线波形为7分频后的基波，且uν=Uνmsinωνt；虚线波形为工频正弦波，且u1=U1msinω1t。结合VVVF原理及等效正弦控制原理可得[9]：

(8)

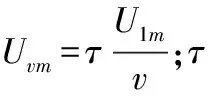
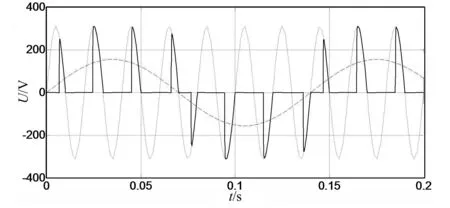
图2　等效正弦的触发角波形图

5　功率因数角的闭环控制

由于斜坡电压的存在，使得过度过程中容易出现电机震荡的现象[10]。经研究表明，这是因为功率因数角φ的存在而引起的，本文通过对功率因数角进行闭环控制的方法来减小电机的震荡[11-12]。

由晶闸管的输出电压公式可知：

(9)

设在t时刻，存在这样的关系：

UL=f(α1,φ1)

(10)

Δt(Δt→0)，UL几乎没有变化，可以忽略不计，则：

UL=f(α2,φ2)

(11)

设α2=α1+Δα，φ2=φ1+Δφ则：

f(α1,φ1)=f(α2,φ2)

(12)

则：

(13)

所以：

(14)

故可得其流程图如图3所示。

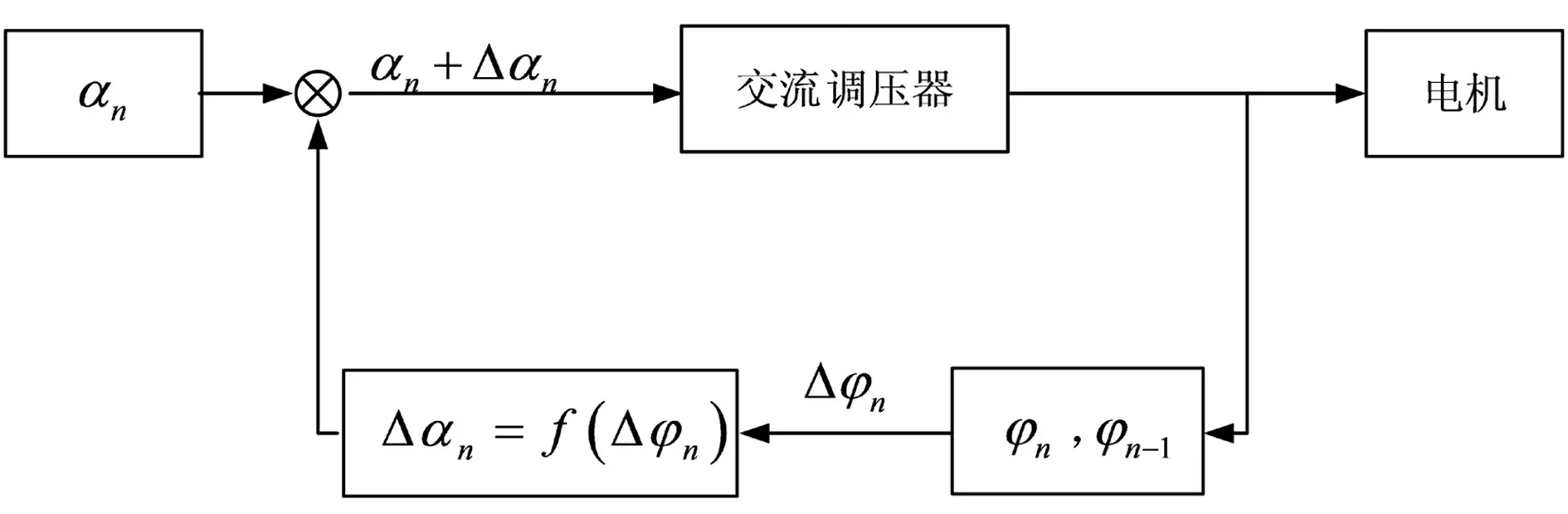
图3　功率因数角闭环控制原理框图

6　仿真分析与研究

借助于MATLAB/Simulink的仿真来进行仿真测验[13]，其中异步电动机PN=5.5 kW、UN=380 V、Rs=1.55 Ω、Rr=1.62 Ω、Ls=9.2 mH、Lr=12.5 mH、Lm=69.31 mH、J=0.02 kg·m2、nN=2 900 r/min，采用频率3.85 Hz→7.14 Hz→12.5 Hz→16.7 Hz→25 Hz→斜坡电压启动→50 Hz的启动方案。启动过程仿真波形如图4所示。

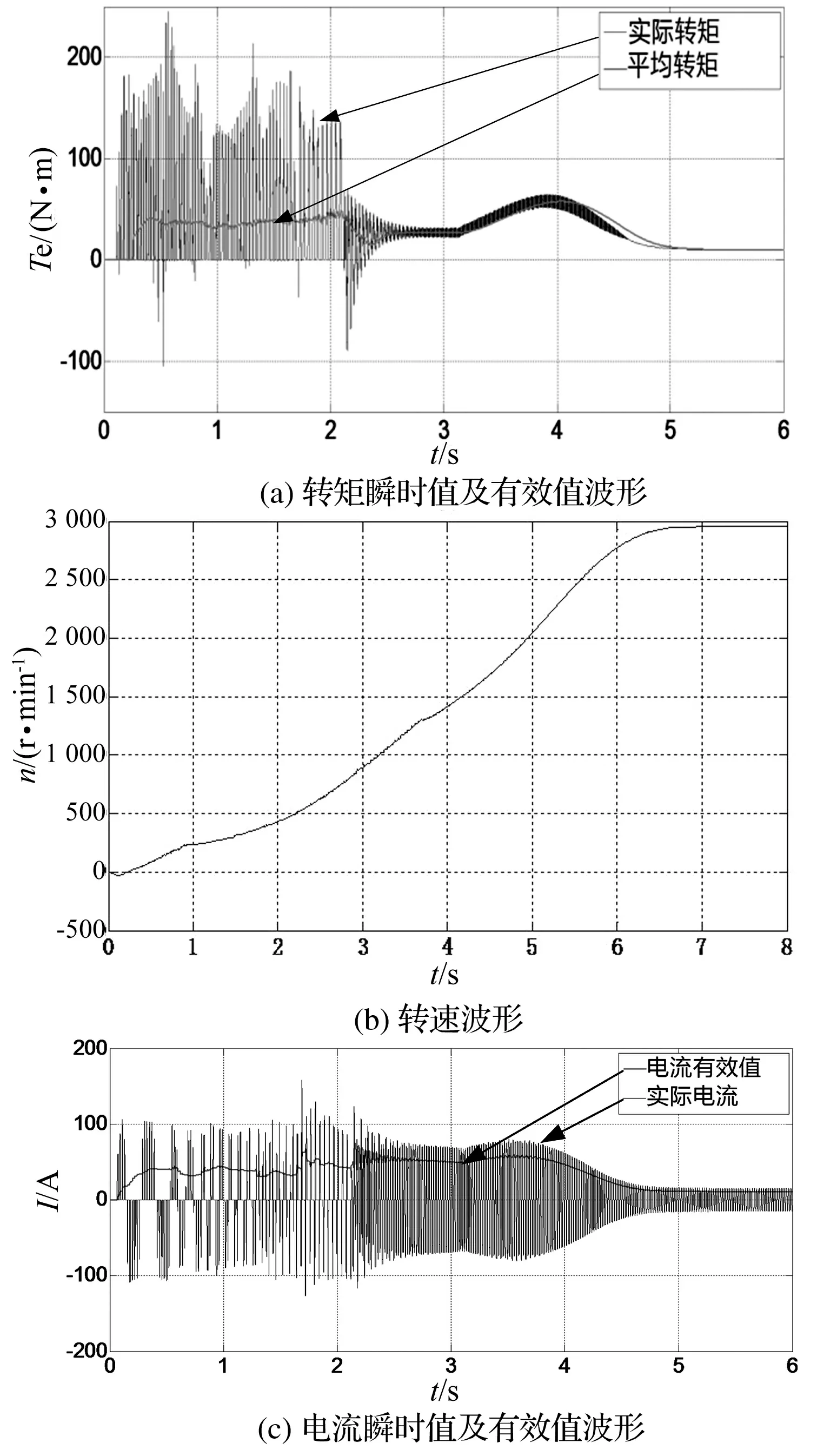
图4　分级变频软启动仿真波形

7　试验

对一台三相异步电机带额定负载进行软启动试验，异步电动机参数如下：UN为380/660 V，IN为11 A，PN为5.5 kW，nN为2 900 r/min，图5和图6分别是4分频和斜坡电压启动所对应的试验波形。

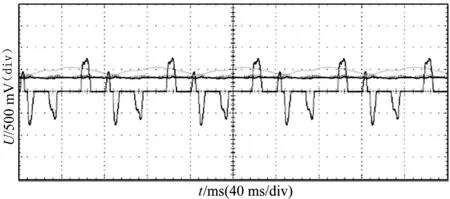
图5　4分频启动波形

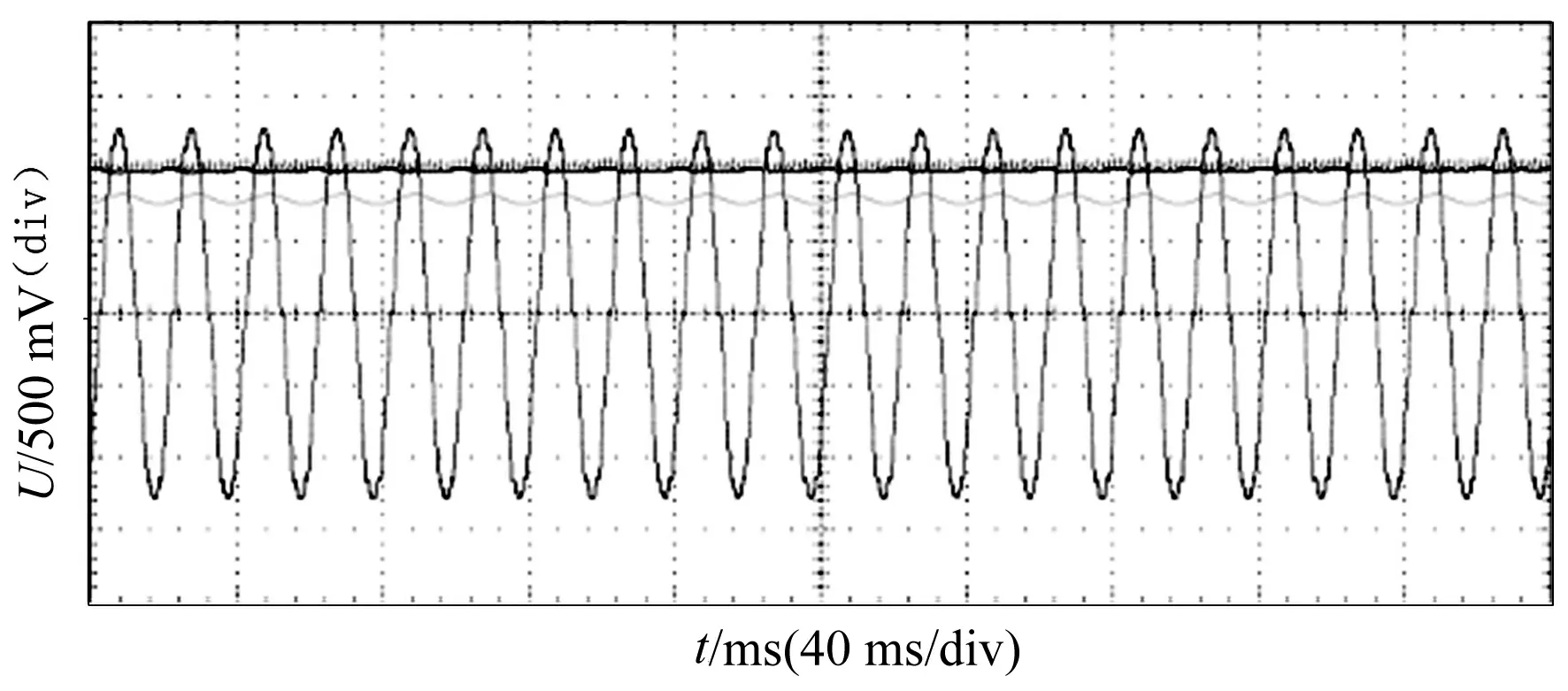
图6　斜坡电压启动波形

由试验波形图可以看出分级变频的软启动控制方式可以降低启动电流的同时，带来比较大的启动转矩。

8　结束语

通过等效正弦分级变频的软启动控制方式可以实现分级变压变频，可以降低启动电流的同时带来比较大的启动转矩，使得满足电机启动的额定转矩。但是分级变频软启动也存在一定技术难题，文中提出的方法可以有效地解决技术上存在的问题。使分级变频的软启动产品用于重载或者满载启动的场合。

参考文献：

[ 1 ] 严垚，王宏华. 异步电动机离散变频软启动技术的发展[J]. 机械制造与自动化，2012，41(6)：196-199.

[ 2 ] 佘致廷，皮玉，周米洋. 感应电机离散变频高转矩软启动器的研究[J]. 电气传动，2010，40(3)：17-19.

[ 3 ] 乔江. 基于DSP的分级变频软启动器的研究与设计[D]. 西安：西安科技大学，2016.

[ 4 ] 孙津济，房建成，王建民.异步电动机软启动过程中的振荡[J]. 电工技术学报，2007，22(2)：16-17.

[ 5 ] 崔学深，张自力，李和明，等. 感应电机电源切换中残压和电压差的研究及最优切换策略[J]. 电力电子技术，2014,48(7)：28-35.

[ 6 ] 肖大志. 基于DSP的异步电动机软启动控制系统研究[D]. 哈尔滨：哈尔滨工程大学，2010.

[ 7 ] DONGHUI L, XIAOBIN D. Research on discrete variable frequency soft starting and electricity-economizing control system of induction motor [C] //International Conference on Electric Information and Control Engineering, Wuhan, 2011.

[ 8 ] 孟彦京，陈君，高泽宇，等. 感应电动机离散变频快速软启动研究[J]. 陕西科技大学学报，2016，34(2)：155-159.

[ 9 ] 王成元，夏加宽，孙宜标. 现代电机控制技术[M]. 北京：机械工业出版社，2014.

[10] 童军，张臻，郭昌永. 电动机软启动功率因数角闭环控制技术研究[J]. 电机与控制学报，2013，17(12)：51-56.

[11] 王毅，赵凯歧，徐殿国. 电机软启动控制系统中功率因数角的研究[J]. 中国电机工程学报，2002,22(8)：82-87.

[12] 孙立伟，孙力. 基于功率因数闭环控制的异步电动机软启动器研究[J]. 微电机，2008,20(3)：13-16.

[13] 佘致延，刘志星，董璞，基于MATLAB/Simulink动态仿真模型的高转矩软启动器研究[J]. 电气传动自动化，2003,25(3)：14-17.