基于预测-校正内点法ATC计算

王永贵，孙超，厉超(南京南瑞继保电气有限公司，江苏 南京　211100)

0　引　言

快速、准确地评估可用输电能力(Available Transfer Capability, ATC)对系统的输电可靠性和电力市场交易顺利进行有着重要的作用。因此国内外专家学者就ATC问题展开了深入的研究[1]。

目前ATC的计算方法大致可分为两类：概率型算法和确定型算法。概率型算法利用概率理论知识来求解系统的ATC，其计算量较大[2-3]。确定型算法主要有：连续潮流法[4]、灵敏度分析法[5]和最优潮流法[6]。其中最优潮流法对复杂非线性规划问题具有较强的处理能力，广泛应用于ATC的计算。

本文从提高ATC计算速度及可靠性的角度出发，基于预测校正内点法计算速度快、鲁棒性好、快速收敛等优点，将预测校正内点法(Predictor-corrector Primal-dual Interior-point Method，PCPDIPM)应用于电力系统ATC计算。通过对模型进行仿真分析，与传统原对偶内点法(Primal-dual Interior-point Method，PDIPM)计算ATC进行比较，验证模型的实用性和算法的有效性及快速收敛性。

1　ATC求解模型

1.1　目标函数

本文将ATC计算的目标函数定义为送电区域对外所有联络线输出功率累加达到最大，忽略输电可靠性裕度和容量效益裕度，即目标函数为[7]:

(1)

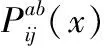
1.2　等式约束

等式约束方程包括发电机节点潮流方程和非发电机节点潮流方程，对于发电机节点：

(2)

式中:k∈i表示第k个发电机接在节点i上;Pgk、Qgk为发电机节点k的有功功率和无功功率；PLi、QLi为节点i的有功功率和无功功率；Vi为节点i电压幅值；Vj为与节点i相连节点的电压幅值；θij为节点i与节点j相角差；Gij、Bij为节点i与节点j间电导和电纳。

对于非发电机节点：

(3)

1.3　不等式约束

不等式约束包含发电机输出功率、负荷、节点电压和线路功率约束，即:

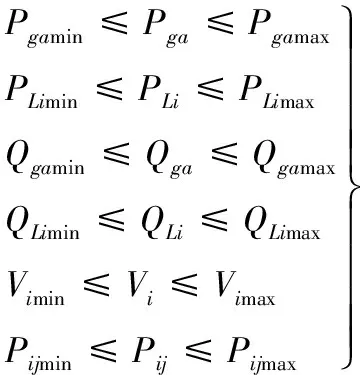
(4)

式中:Pga、Qga分别为发电机a的有功出力和无功出力;PLi为节点i的有功功率;QLi为节点i无功功率;Vi为节点i的电压;Pij为线路功率;j∈i表示节点j与节点i相连。

2　预测-校正内点法数学模型描述

2.1　原对偶内点法概述

假设x∈Rn，h(x)∈Rm，g(x)∈Rr，PDIPM算法求解最优解问题的基本原理如下几个步骤[8-12]：

(1)设置松弛变量l、u，均为r维列向量，且满足l>0、u>0，使不等式约束等式化：

(5)

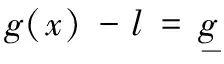
(6)

(2)将原优化问题变换为如下新的优化问题：

(7)

s.t.h(x)=0

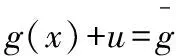
式中：μ′为扰动因子。式(7)后面两项为惩罚项，当li→0或者ui→0，目标函数值趋于无穷大，为此要使式(7)与原目标函数具有相同最优目标值，则在最优运行点上必须满足两个条件：一是li>0并且ui>0；二是μ′→0。

优化问题(7)的拉格朗日函数：

(8)

式中：y∈Rm，z∈Rr，w∈Rm，且z>0、w<0，y、z、w均为拉格朗日乘子。为了求得函数的极小值，需对函数变量求一次偏导，偏导值为零。

联立求解可得：

(9)

式中：Gap=lTz-uTw称为对偶间隙，也称补偿间隙。研究证明当Gap→0,μ′→0时，优化问题能获得最优解。为了使算法具有更好的收敛性，对式(9)进行修改得如下表达式：

(10)

式中：σ∈(0,1)称为中心参数。

(3)利用库恩-塔克(Karush-Kuhn-Tucker，KKT)条件得到一系列的非线性方程。

(4)最后用牛顿-拉弗森法来求解非线性方程组并通过对偶间隙判断收敛性。

综上所述，原对偶内点法求解ATC的算法流程如图1所示，图中kmax为最大迭代次数，ε为收敛精度，本文取ε=10-6。

图1　原对偶内点法求解ATC的流程图

2.2　预测-校正内点法概述

PCPDIPM是在PDIPM基础上进行改进，PDIPM在求解障碍函数扰动因子m时，中心参数s是固定不变的，而PCPDIPM在每次迭代时都对中心参数s进行修正，提高收敛速度[13-15]。

(11)

(12)

整理可得：

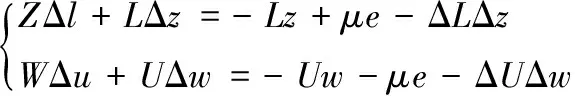
(13)

于是修正方程变为：

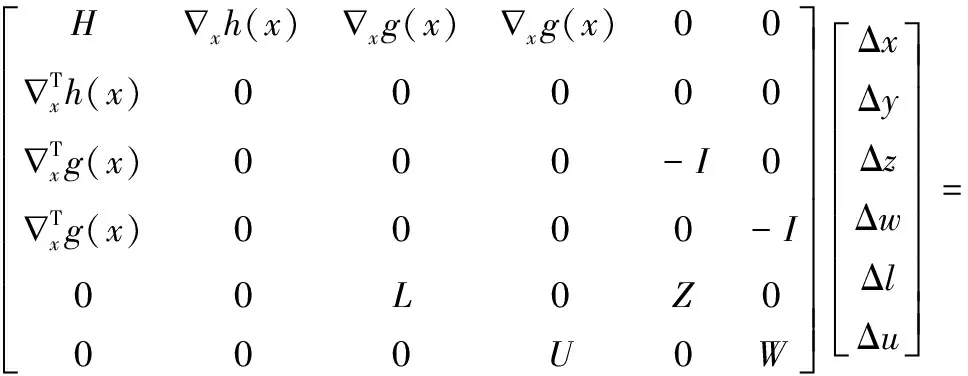
(14)

式中：

Lx-co=xg(x)[L-1(-μe+ΔLafΔzaf)+U-1(μe+ΔUafΔwaf)]

整个等式可记作：

(15)

预测步求出仿射方向的修正量：

3.1.3 未按要求总结液体出入量记录 入量错误调查中，肠外营养液记录不准确128例次占76.65%。对于进行肠内外营养支持治疗或静脉输液时，护理人员往往在更换液体时即将所更换的液体记录在护理监护单入量这一栏内，交接班以后，总结液体入量时，下一班护士往往只根据护理监护单上的记录值，将记录的液体总量相加，而实际入量与记录量可能并不一致，致使总结的液体入量与实际的液体入量不统一，影响了对患者病情的观察和判断。

(16)

校正步求出校正方向的修正量：

(17)

因此总牛顿法方向的修正量为：

Δω=Δωaf+Δωco

(18)

PCPDIPM求解ATC问题的算法流程如图2所示，其在预测步和校正步的计算步骤如下：

(1)预测步

①设定中心参数σ=0。

②求解仿射方向修正量。

③确定迭代步长。

⑤求得扰动因子μ：

(19)

(2)校正步

①根据仿射方向修正量求得校正方向的常数项。

②求得校正方向的修正量。

图2　预测—校正内点法求解ATC的流程图

3　算例分析

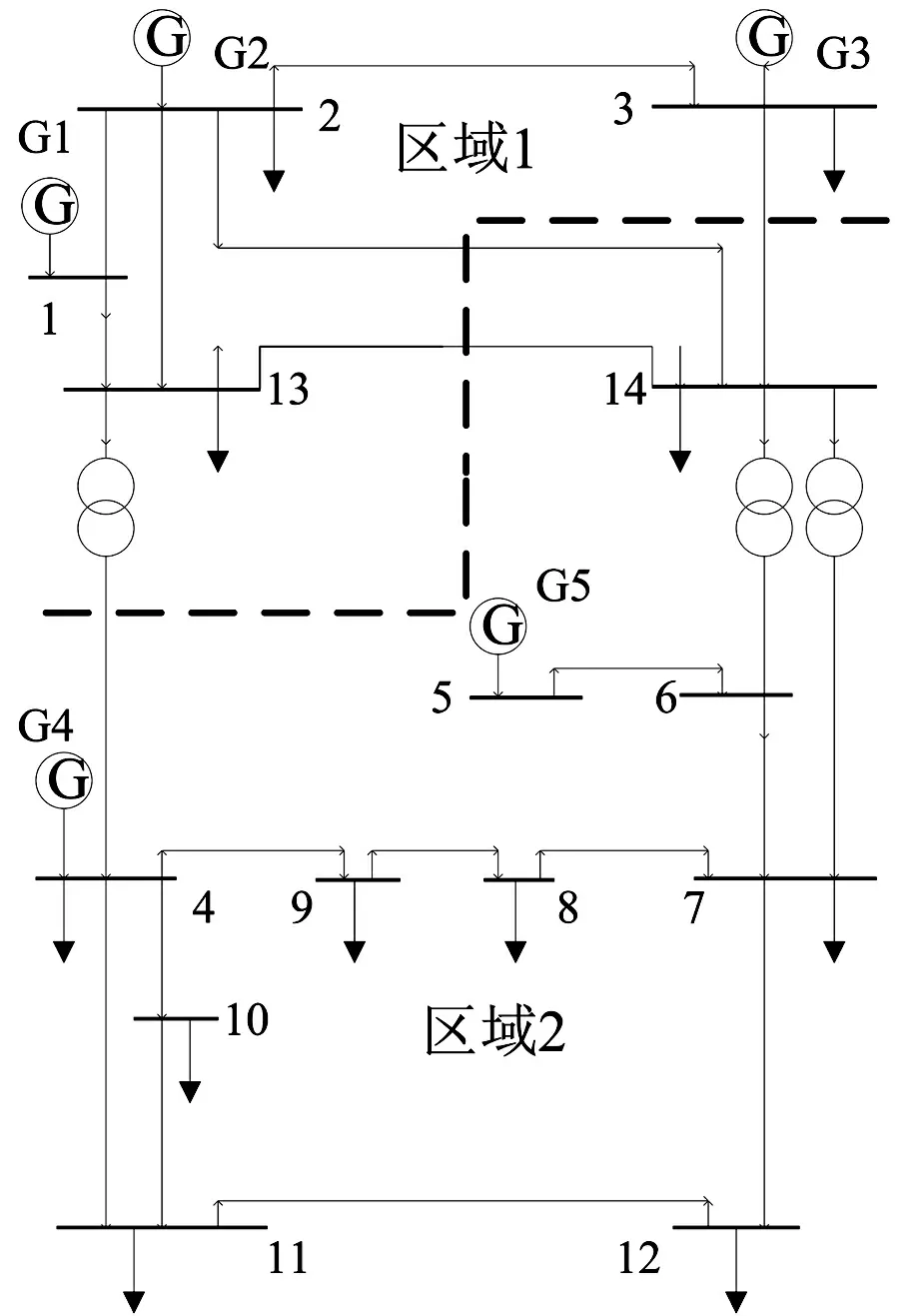
图3　IEEE 14节点系统

本文以IEEE 14节点系统、IEEE 30节点系统、IEEE 57节点系统为例验证算法的有效性和实用性。区域划分以IEEE 14、IEEE 30节点系统为例，划分情况如图3和图4所示。

IEEE 14节点系统区域划分图

IEEE 30节点系统区域划分图

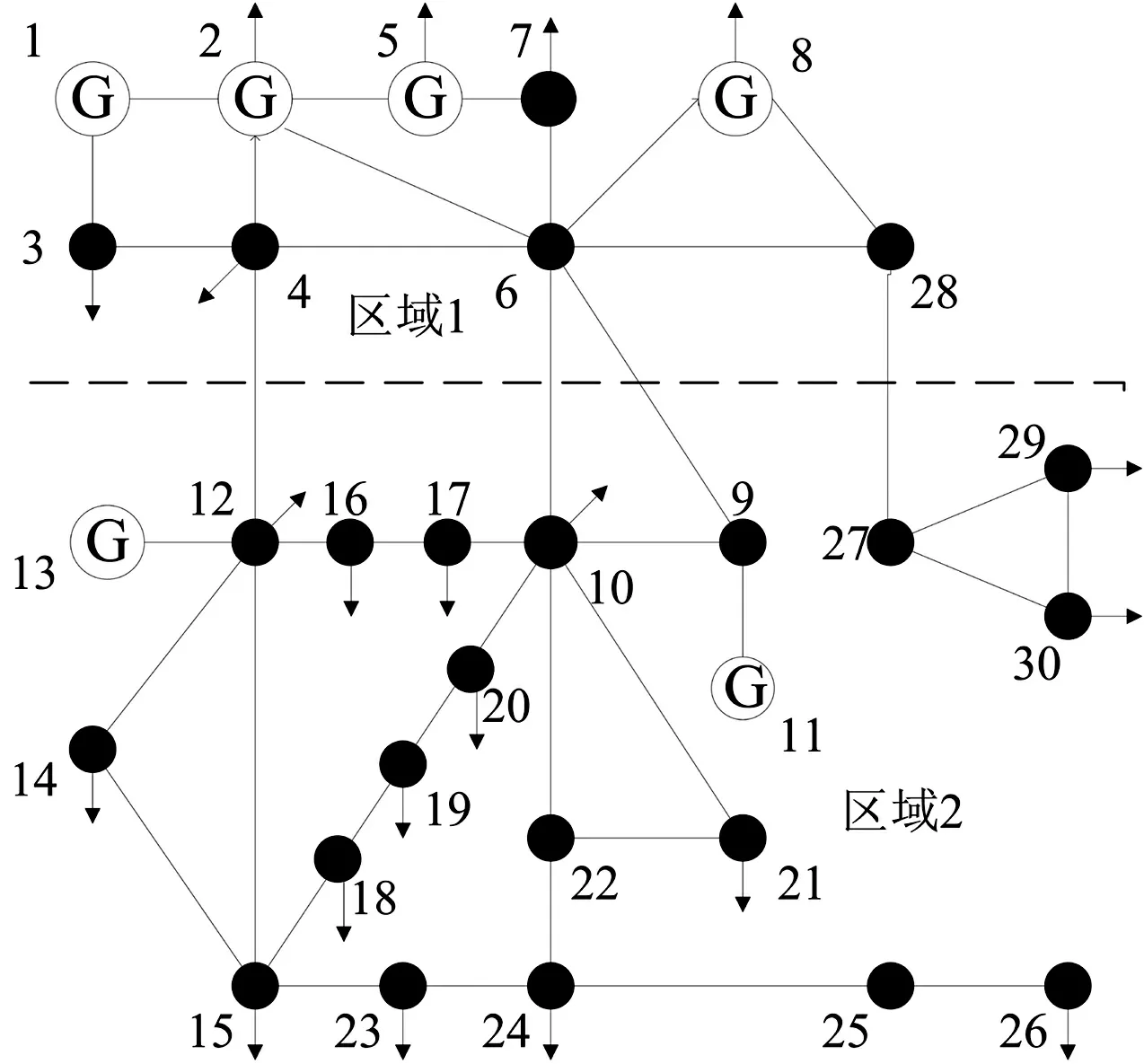
图4　IEEE 30节点系统

在相同的ATC目标函数及约束条件下，分别使用PDIPM和PCPDIPM两种算法计算不同算例系统的可用输电能力，计算结果及迭代次数如表1所示。

表1　PDIPM与PCPDIPM迭代次数比较与区域联络线功率

由表1可知， PDIPM算法和PCPDIPM算法均能快速收敛，内点法对于提高ATC计算速度方面有着积极作用，对比收敛迭代次数可知，在同等条件下，改进后的PCPDIPM算法的迭代次数比PDIPM算法少，收敛速度更快，PCPDIPM在提升ATC计算速度上有着更大的优势。

4　结束语

本文建立了基于PCPDIPM算法计算ATC的模型，通过对IEEE 14节点系统、IEEE 30节点系统、IEEE 57节点系统为例验证了算法的有效性和实用性，并与PDIPM算法计算ATC的方法进行比较，对比仿真结果可知，PCPDIPM和PDIPM两种算法均能快速收敛，内点法对于提高ATC计算速度方面有着积极作用；对比收敛迭代次数可知，在同等条件下，改进后的PCPDIPM算法的迭代次数比PDIPM算法少，收敛速度更快，PCPDIPM算法在提升ATC计算速度上有着更大的优势。

参考文献：

[ 1 ] 方略斌，蔡金锭．考虑发电报价和N-1安全约束的ATC建模与仿真[J]．电力科学与技术学报，2011，26(2)：101-106．

[ 2 ] 李庚银，高亚静，周明．可用输电能力评估的序贯蒙特卡罗仿真法[J]． 中国电机工程学报，2008，28(25)：74-79．

[ 3 ] RODRIGUES A B，DA SILVA M G．Probabilistic assessment of available transfer capability based on Monte Carlo method with sequential simulation[J]．IEEE Transactions on Power Systems，2007，22(1)：484-492．

[ 4 ] 王俊，蔡兴国，张占安．考虑电压和暂态稳定性的可用输电能力计算[J]．电网技术，2011，35(10)：88-93．

[ 5 ] GHAWGHAWE N D，THAKRE K L．Application of power flow sensitivity analysis and PTDF for determination of ATC[C]．IEEE International Conference on Power Electronics，Drives and Energy Systems (PEDES-2006) New Delhi，2006．

[ 6 ] 何鑫，李国庆．基于混沌内点法的可用输电能力计算[J]．电网技术，2011，35(11)：130-135．

[ 7 ] 汪峰，白晓民．基于最优潮流方法的传输容量计算研究[J]．中国电机工程学报，2002，22(11)：36-40．

[ 8 ] 张磊，杨洪明，刘文洵．基于矩不确定分布鲁棒的微网经济调度[J]．电力科学与技术学报，2015，30(2)：35-40．

[ 9 ] 周任军,吴潘．基于电压稳定裕度的无功优化规划[J]．电力科学与技术学报，2010，25(1)：86-90．

[10] 卫志农，季聪，孙国强，等．含VSC-HVDC的交直流系统内点法最优潮流计算[J]． 中国电机工程学报，2012，32(19)：89-95．

[11] 王锡凡，方万良，杜正春．现代电力系统分析[M]．北京：科学出版社，2003.

[12] 江全元，耿光超．含高压直流输电系统的内点法最优潮流算法[J]．中国电机工程学报，2009，29(25)：43-49．

[13] 覃智君，阳育德，吴杰康．矢量化动态最优潮流计算的步长控制内点法实现[J]．中国电机工程学报，2009，29(7)：52-58．

[14] 徐进东，丁晓群，覃振成，等．基于非线性预报-校正内点法的电力系统无功优化研究[J]．电网技术，2005，29(9)：36-40．

[15] 覃振成，乐秀璠，蓝澜，等．基于改进非线性预报-校正内点法的最优潮流[J]．电力系统自动化，2005，29(9)：25-30．