基于Voigt与Reuss模型的岩土二元介质破损规律

杨瑞敏，丁建文，章振宁，吴伟东(.安徽科技学院建筑学院，安徽 滁州　3300； .东南大学岩土工程研究所，江苏 南京　0096)

天然沉积软黏土具有非均质、多孔等结构性特征。沈珠江等[1-6]认为必须考虑土体变形中结构的破坏，建立结构性土模型是当代土力学的核心问题，为此一种新的岩土力学分析理论——岩土破损力学被提出。岩土破损力学[3-9]是一种基于准连续介质进行宏观分析的力学理论，研究对象为破碎严重的岩体和结构性土体。结构性岩土体被抽象为由胶结元与摩擦元组成的二元介质，加载过程中胶结元逐步破损，并向摩擦元转化。沈珠江[4]基于非均匀材料的均匀化理论，推导出变形协调条件下岩土二元介质的破损力学方程。而岩土二元介质中，胶结元与摩擦元不仅变形是协调的，应力也是连续的。复杂应力状态下二元介质破损规律的研究是岩土破损力学研究的热点问题。考虑胶结元与摩擦元的应力连续性条件探讨二元介质的破损规律是破损力学的一个重要补充。在破损力学的理论框架下，本文将结构性岩土体抽象为由胶结元和摩擦元组成的二元介质，基于Voigt和Reuss模型分别导出满足变形协调和应力连续条件的张量形式的岩土破损力学本构方程，探讨三轴复杂应力状态下岩土二元介质的破损规律、荷载及变形分担情况。

1　基于Voigt模型的岩土二元介质本构关系

岩土体类似于复合材料，可借用复合材料的均匀化理论进行分析[12-13]。从岩土体中取出一个代表单元，宏观上无限小，在岩土体中可被当作一个点，微观上无限大，包含岩土体的所有力学与几何统计信息。设代表单元的体积为V，胶结元与摩擦元的体积分别为VI和VF，则胶结元和摩擦元的平均应力与应变可定义为：

令λ=VF/V，为体积破损率，则二元介质的平均应力与平均应变为：

其中C为局部化应变张量。

将式(5)代入式(4)可得

胶结元、摩擦元的平均应力、应变满足如下关系：

其中DI、DF分别为胶结元与摩擦元的弹性刚度张量。

将式(5)、(6)代入式(7)得：

将式(8)、(9)代入式(3)可得

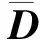
其中B=I-(1-λ)C为破损张量。将式(11)代入式(10)可得

式(13)为应力张量表示的岩土破损力学本构方程，破损张量B是与体积破损率、局部化应变张量有关的内变量，称为应力分担率张量。σI、σF分别为胶结元和摩擦元中任意一点的应力张量。

由式(11)可得应力分担率张量

2　基于Reuss模型的岩土二元介质本构关系

将式(15)代入式(3)可得

其中SI、SF为胶结元与摩擦元的柔度张量。

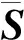
由式(18)可得变形分担率张量：

3　讨　论

第1节中基于Voigt模型推导出以刚度张量表示的岩土二元介质破损力学本构方程和应力分担率张量B。若将局部化应变张量C退化为标量形式c，则B=I-(1-λ)C可退化为标量形式b=1-(1-λ)c。单向压缩时，式(14)可退化为：

式中E、EI、EF分别为二元介质、胶结元和摩擦元的弹性模量。纯剪切时，式(14)可退化为

式中μ、μI、μF分别为二元介质、胶结元及摩擦元的剪切模量。

对于各向同性材料，当ν=νI=νF时有[4]

式(11)可退化为[4]

式(10)可退化为[4]

当ν≠νI≠νF时，bE≠bμ，此时式(24)为

式(28)中ν、νI、νF分别为二元介质、胶结元及摩擦元的泊松比。

对于正交各向异性材料，分别在3个主方向(j=1,2,3)上进行单向压缩时，则式(14)可退化为

纯剪切时，式(14)可退化为

式(29)、(30)中Ej、EIj、EFj与μjk、μIjk、μFjk，k=1,2,3,j=1,2,3,j≠k分别为二元介质、胶结元和摩擦元的3个主方向进行单向压缩的弹性模量和纯剪切的剪切模量。

式(25)—(27)与沈珠江等推导的结果[1-9]是一致的，但沈珠江等的结果仅满足胶结元与摩擦元变形协调条件，且岩土破损力学基本方程为标量形式，没有考虑胶结元与摩擦元应力的连续性，不能直接用于实际复杂应力状态岩土实际边值问题的有限元计算。

纯剪切时，式(22)可退化为

对于各向同性材料，当ν=νI=νF时可得

式(18)可退化为

式(19)可退化为

对于正交各向异性材料，分别在3个主方向(j=1,2,3)上进行单向压缩时，有

纯剪切时，有

式(37)、(38)中下标j=1,2,3,k=1,2,3,j≠k。

Reuss模型满足胶结元与摩擦元应力的连续性条件，但没有考虑变形的协调性。实际的岩土二元介质中，胶结元与摩擦元不仅需要满足变形协调条件，而且还要满足应力连续性条件，要得到一个能同时考虑胶结元与摩擦元变形协调和应力连续性的严格意义的岩土二元介质本构关系几乎不可能。Hill[14-15]、Budinansky等[16]利用自洽法可使二元介质中胶结元与摩擦元的变形协调和应力连续性条件在弱形式下得到满足。本文推导的岩土破损力学本构方程，可为结构性岩土体实际边值问题的有限元计算提供理论依据，同时为进一步研究实际复杂应力状态下各向异性岩土体的破坏机制提供有效的途径。

4　算例分析

假定胶结元为各向同性、理想脆弹性体，弹性模量与泊松比分别为EI、νI(均为常量)；摩擦元的弹性模量与泊松比分别为EF、νF(均为变量)。摩擦元的弹性模量随着围压的增加而增加，即

EF=kFσ3。

(39)

其中：kF为比例系数；σ3为周围压力。

摩擦元的泊松比与应力水平有关，且随着应力水平s的增加而增加[17]，即

νF=νFi+(νFf-νFi)s。

(40)

其中：DF、FF为试验参数；Pa为大气压力，取Pa=105Pa。

Viogt模型[10]认为：胶结元与摩擦元并联，二元介质表现为脆弹性，弹性模量与泊松比分别为E、ν；Ruess模型认为[11]：胶结元与摩擦元串联，二元介质表现为线性硬化。二元介质的弹性模量满足

E=kσ3。

(42)

其中：k为比例系数；σ3为周围压力。岩土二元介质的泊松比满足

ν=νi+(νf-νi)s。

(43)

其中：νf为破坏时的切线泊松比，可取νf=0.49；νi为初始切线泊松比，可由下式确定：

其中G、F为试验参数。

胶结元为各向同性材料时，弹性刚度张量DI与柔度张量SI可分别由下式计算：

(DI)ijkl=λIδijδkl+μI(δikδjl+δilδjk)。

(45)

(46)

式(45)、(46)中：λI、μI为拉梅常数；δij为Kronecker符号。拉梅常数与弹性模量、泊松比满足如下关系：

已知胶结元和二元介质的弹性模量、泊松比分别为EI=8 200 kPa，E=4 600 kPa，νI=0.22，ν=0.26，式(41)中参数GF=0.36，FF=0.6，(ν1-ν3)f=600 kPa。令kF=10，则摩擦元的弹性模量为EF=10ν3，利用Maple软件计算可得应力分担率张量B的非零分量：Biiii,Biijj,Bijij，i≠j，i,j=1,2,3的演化规律如图1—3所示，而其他分量均为0。

图1　不同σ3下Biiii与s关系曲线

由图1可知，在围压σ3一定时，Biiii,i=1,2,3随着应力水平s的增大而增大，当应力水平s一定时，Biiii均随着围压σ3的增大而增大，表明在3个主应力方向胶结元均逐步破损，在抵抗轴向压力中发挥的作用逐渐减小。由图2可知，在围压σ3一定时，Biijj,i≠j,i,j=1,2,3随着应力水平s的增大而增大，当s=0时Biijj为负数，是由于在某一主应力(如大主应力σ1)方向施加主压应力会在其他2个主应力(如σ2,σ3)方向上产生拉应力；但是随着大主应力方向应力水平s的增大，σ2、σ3方向上胶结元由受拉状态转化为受压状态，并逐渐破损。应力水平s一定时，随着围压σ3的增大，Biijj,i≠j,i,j=1,2,3逐步减小。由图3可知，围压σ3一定时，随着应力水s的增大，Bijij,i≠j,i,j=1,2,3逐步减小，表明胶结元在抵抗剪切力中发挥的作用逐渐增大；当应力水平s一定时，随着围压的增大，Bijij,i≠j,i,j=1,2,3逐步增大，表明胶结元在抵抗剪切力中发挥的作用逐渐减小。

图2　不同σ3下Biijj与s关系曲线

图3　不同σ3下Bijij与s关系曲线

图4　不同σ3下与s关系曲线

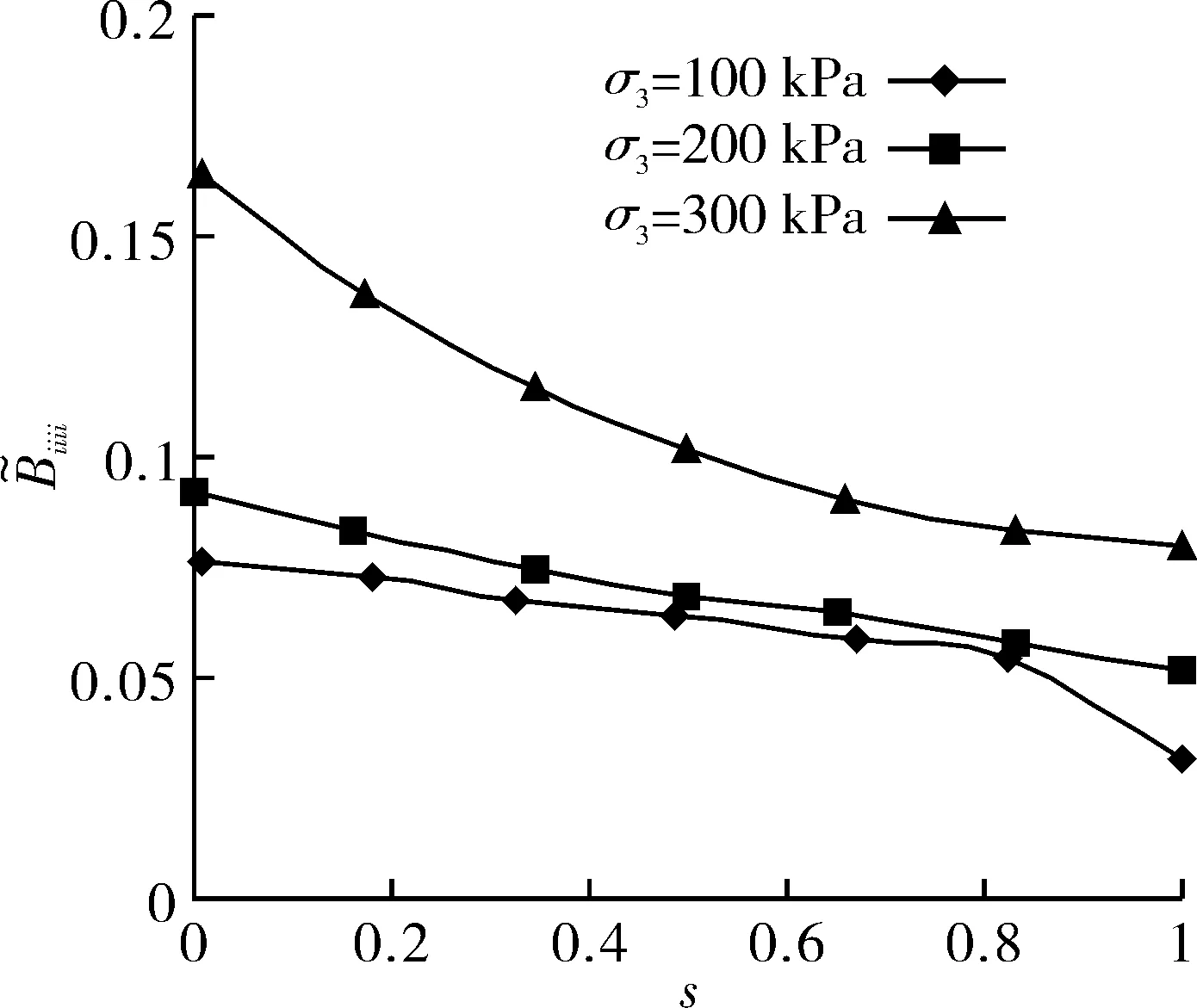
图5　不同σ3下与s关系曲线

图6　不同σ3下与s关系曲线

5　结　论

基于Voigt和Reuss模型推导出岩土二元介质破损参数为张量形式的破损力学方程，得到如下结论：

1)岩土二元介质的破损行为与胶结元、摩擦元的物理力学特性、围压和应力水平有关。

2)应力分担率Biiii随应力水平s和围压σ3的增大而增大，表明在主应力方向由于胶结元的破损，在抵抗轴向压力中发挥的作用逐渐减小。

3)应力分担率Biijj在s=0时为负值，随应力水平s的增大而增大，当s>0.6后逐渐变为正值，表明随着大主应力施加，在中、小主应力方向胶结元由受拉转化为受压，并逐步破损；Bijij随应力水平s的变化不大。

[1]沈珠江. 理论土力学[M]. 北京：中国水利水电出版社，2000.

[2]沈珠江，陈铁林. 岩土破损力学：基本概念、目标和任务[C]//中国岩石力学与工程大会第七次学术会议论文集. 北京：中国科学技术出版社，2002.

[3]沈珠江. 岩土破损力学与双重介质模型[J]. 水利水运工程学报，2002(4)：1.

[4]沈珠江. 岩土破损力学：理想脆弹塑性模型[J].岩土工程学报，2003，25(3)：253.

[5]沈珠江，胡再强. 黄土的二元介质模型[J]. 水利学报，2003，34(7)：1.

[6]沈珠江，陈铁林. 岩土破损力学：结构类型与荷载分担[J]. 岩土力学与工程学报，2004，25(13)：2137.

[7]SHEN Z J. Binary medium modeling of geological material [C]// International Conference of Heterogeneous Materials Mechanics. Chongqing: [s.n.], 2004: 581.

[8]沈珠江，陈铁林. 岩样变形和破坏过程的二元介质模拟[J]. 水利水运工程学报，2004(1)：1.

[9]沈珠江，刘恩龙，陈铁林. 岩土二元介质模型的一般应力应变关系[J]. 岩土工程学报，2005，27(5)：489.

[10]VOIGT W. Über die Beziehung zwischen den beiden Elastiziä tskonstanten isotroper Körper[J]. Wied Ann, 1889, 38: 573.

[11]REUSS A. Berchung der Fiessgrenze von Mischkristallen auf Grund der Plastiziä tsbedingung für Einkristalle Z[J]. Angew Math Mech, 1929, 9: 49.

[12]ANTHOINE A. Derivation of the in-plane elastic characteristics of masonry through homogenization theory [J]. Int J Solids and Structures, 1995, 32(2): 137.

[13]WANG J G, LEUNG C F, ICHICAWA Y A. Simplified homogenization method for composite soils [J]. Computers and Geotechnics, 2002, 8(3): 124.

[14]HILL R A. Self-consistent mechanics of composite materials [J]. Mech Phys Solids, 1965, 13: 213.

[15]HILL R A. Continuum micro-mechanics of elastoplastic polycrystals [J]. Mech Phys Solids, 1965, 13: 89.

[16]Budiansky B, WU T Y. The eoretical prediction of plastic strains of polycrystals [C]// Proc 4th US Nat Con Appl Mech. 1962: 1175.

[17]钱家欢，殷宗泽. 土工原理与计算[M]. 北京：中国水利水电出版社，1996.