一种基于神经网络和遗传算法的桥梁加速度传感器优化布置方法

袁　灿，唐川田，李文钊(. 重庆交通大学信息科学与工程学院，重庆　400074; . 成都理工大学信息科学与技术学院，四川 成都　60059)

采用加速度传感器获得桥梁的自振频率、振型、阻尼比等动力特征，对桥梁健康状态的监测起着至关重要的作用。保证健康监测系统所采集到的数据能够准确反映结构工况的参数信息和数据，是准确分析大桥结构状况、进行结构损伤识别和安全评估的依据。其关键技术之一是传感器测点的布置。传感器数量太少不能反映桥梁真实健康状态；传感器数量太多会导致成本偏高，浪费资源：因此，传感器的布置既要考虑获得最全面、最可靠的数据，又要兼具良好的经济性。

目前研究加速度传感器优化布置的方法主要有以下几类。Kammer[1]提出的有效独立法是目前工程中应用较为广泛的方法之一，也有研究者对其改进[2]。该方法首先将所有可能的测量点的模态矩阵形成相应的信息阵，然后将各个测点对信息阵的作用进行比较，剔除其中对秩影响最小的点，最终使Fisher信息阵的值更优。该方法往往只能寻找到目标函数的次优解而不是最优解。序列法是通过逐步消去或逐步累积的方法进行布置，如EI法[3]。逐步消去法本质是根据所有已有节点逐步消除不必要的传感器位置，同时做评估；逐步累积法则与逐步消去法相反。无论哪种，起始点位置不同，布置方案可能不同，通常情况下都只能得到问题的次优解。基于群智能优化算法的传感器优化布置在近几年研究较多，如赵宇等提出的基于免疫算法的布置方法[4]、伊廷华等提出的基于病毒猴群算法的布置方法[5]、Yi等提出的基于协作爬猴算法的布置方法[6]等。这类算法由于采取非数值计算的概率性随机搜索模式，突破了传统优化方法基于数值计算的确定性搜索模式，因而不易收敛于局部最优解。

综上所述，目前表现最好的方法是群智能优化算法。该类算法通过随机搜索的方式找到满足桥梁加速度传感器布置的评价准则(如MAC矩阵、Fisher信息阵等)的最优值。实质上该类算法是向优化方向随机搜索并不断迭代，比起确定性搜索大大减小了算法复杂度；但是，它是通过桥梁自由度与评价准则的直接关系来寻优，而这个关系网络分布未知且很复杂，因此搜索时容易陷入局部最优。为此，笔者将神经网络和随机算法结合，尝试利用神经网络建立布置方案与评价准则的简单关系网络，再利用随机算法来寻优，减小陷入局部最优的概率。

1　基于神经网络和遗传算法的传感器优化布置总体方案

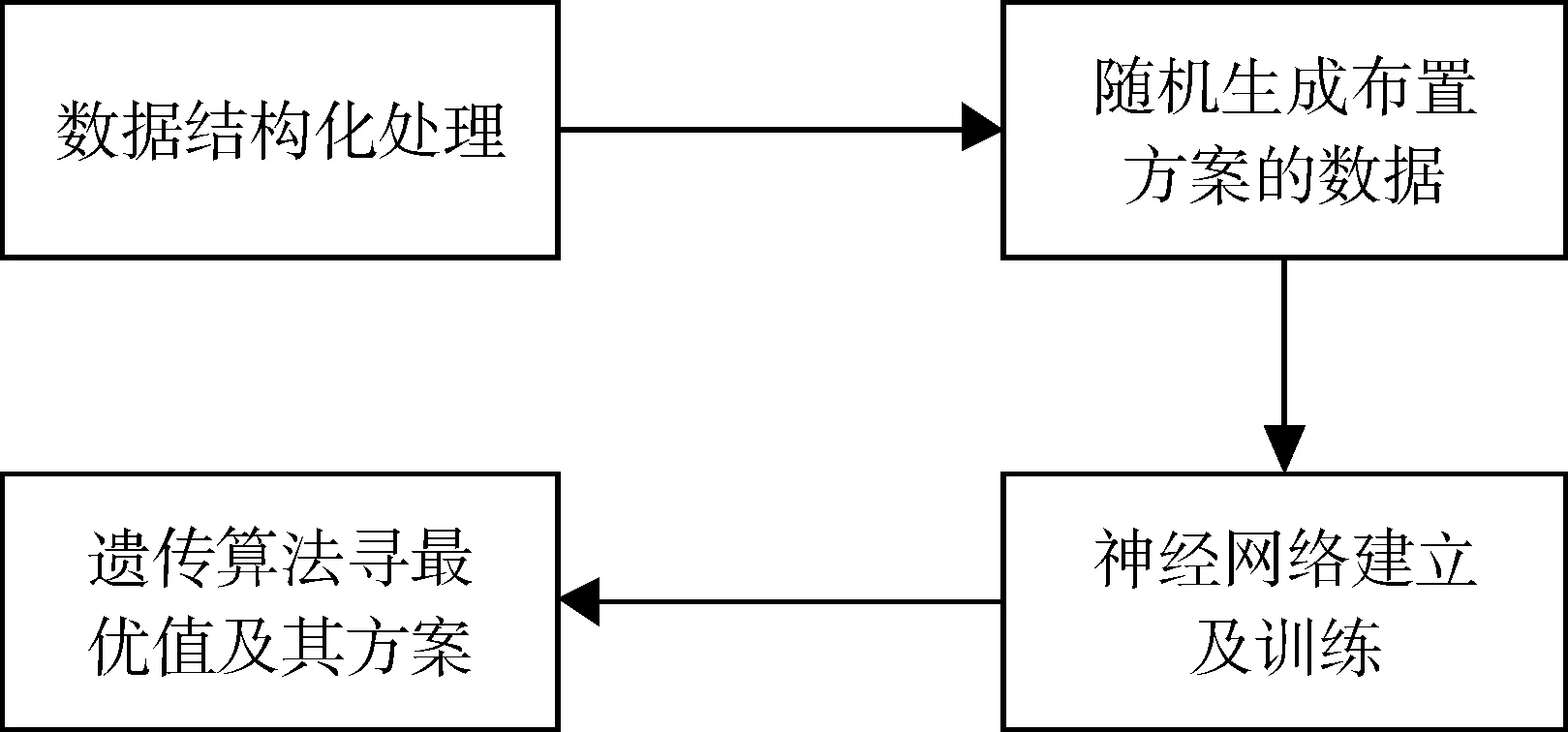
图1　总体方法思路流程

2　数据结构化及处理

2.1　二值化编码

为清晰地表示各个节点的位置和布置情况，将桥梁沿着主梁从左至右等间距依次编号，用0和1来表示是否布置，即若该点未布置则为0，已布置则为1，如图2所示。

图2　编号及布置情况示意图

2.2　加速度传感器布置评价准则计算

根据结构动力学原理，结构的各阶振型之间是相互正交的，但实际测量时的自由度远远小于结构本身的自由度，而且测量过程中由于测试仪器的精度和测量噪声等因素的影响，测得的模态向量不能保证其正交性，甚至由于向量之间的空间交角太小而使有的模态丢失；因此，在选择测点的位置时应该使测量的模态向量保持较大的空间交角。MAC(modal assurance criterion)矩阵是衡量振型线性独立性的最好工具[7]。其公式为

式中：φi和φj分别是第i阶和第j阶计算阵型在n个传感器所对应的自由度的值。当MAC=1时表明第i阶模态向量和第j阶模态向量交角为零，两向量不可分辨；当MAC=0时表明第i阶模态向量和第j阶模态向量交角为90°，即两向量相互正交，可以很容易识别[7]。MAC矩阵的非对角元素最大值越小，MAC矩阵整体就越小，正交性也就越好，这可以作为加速度传感器配置效果的一个评价指标。

本文首先利用ANSYS仿真软件对桥梁进行建模并通过模态分析获得每个有限元节点同一方向的自由度值，然后选择沿主梁的所有有限元点作为可布置节点，用矩阵φn表示第n阶已布置的节点的自由度集合，然后代入式(1)计算出各阶之间同一振动方向的MAC矩阵。不同的布置方案由于自由度值不同MAC也就不同，这样根据布置方案和模态数据很容易计算出各个布置方案的MAC矩阵，并选出矩阵中最大值作为该方案评价指标。

2.3　随机生成布置方案数据

表1　随机生成数据

3　神经网络训练

采用带有单个隐藏层的神经网络[8]拓扑结构如图3所示。

图3　单隐藏层神经网络拓扑结构

图3中：x1,x2,…,xn是神经网络的输入值，O1,…,Ok是神经网络的输出值。输入层的数量由桥梁可布置传感器的节点数n确定。隐含层的层数和数量由实际数据量大小确定。输出层就是MAC矩阵中最大值。整个神经网络输出表示为：

式中：Ok为输出层输出；Hj为隐含层输出；ωjk、ωij为连接权值；bk、aj为阈值；G和s为激励函数，该函数有多种，典型的包括双曲正切函数、sigmoid函数等。sigmoid函数表示为

sigmod(a)=1/(1+e-a)。

(4)

通过最小化误差来不断调整权值等参数。每一个训练样例的误差函数为

ek=Yk-Ok。

(5)

权值和阈值更新函数为：

ωjk=ωjk+ηHjek；

(7)

bk=bk+ek。

(9)

式中η为学习率。

神经网络及其相关算法目前已经较成熟，在MATLAB的工具中建立模型导入个人处理后的数据就能进行训练并保存训练好的网络(*.mat格式)。它实质上包含了最终所有权值和阈值的数据集，也可以看作是求得各个参数的复合函数。

4　遗传算法寻优

遗传算法[9](genetic algorithms)是模拟自然遗传机制和生物进化论而成的一种并行随机搜索最优化方法，具有高效的启发式搜索、并行计算等特点。该算法的基本操作如下。

1)种群初始化。对个体进行基因编码，将桥梁每个可布置节点看作一个基因，每一种布置方案就是基因组合的染色体，因此该问题可抽象成求神经网络模型中最优染色体问题。

2)适应度函数。适应度函数直接对繁衍的后代进行评估，判断是否为最优秀的后代。这里采用训练好的神经网络模型的输出函数，因此只须把训练好的权值和阈值代入式(2)和式(3)即可。

3)选择操作。从旧群体中以一定概率选择优秀个体到新群体中，以得到较优秀的布置方案群体，被选中的概率依赖于适应度值，个体适应度值越小，被选中的概率越大。

式中f(xi)表示适应度值。

4)交叉操作。交叉过程从群体中任选2种布置方案，随机选择2个位置进行交换，并满足交换后的布置或未布置的数量不变。交叉方法采用实数交叉法，第m个染色体与第n个染色体在j位的交叉方法为：

式中b为[0,1]的随机数。

5)变异操作。从群体中任选一个个体，选择染色体中的2点进行变异以产生更优秀的个体，同时满足变异后的布置或未布置的数量不变，选取第i个个体第j个基因进行变异，变异操作为：

式中，amax为基因aij上界；amin为基因aij下界；f(g)=r2(1-g/Gmax)；r2为随机数；g为当前迭代次数；Gmax为最大进化次数；r为[0,1]的随机数。

将训练好的网络模型通过遗传算法搜索最优值，其算法流程如图4所示。

图4　算法流程图

5　仿真

采用ANSYS 14.0建立桥梁有限元模型，从左至右沿主梁的有限元节点依次编号，共54个节点，通过模态分析得到前5阶x、y和z3个方向的自由度值，这里讨论在y方向的振型。

图5　桥梁有限元模型

考虑在这54个节点中布置15个传感器，同时计算出该方案的MAC矩阵的非对角元素最大值，利用随机方法生成5 100组布置方案和对应MAC值，分别作为输入和标签。由于有54个节点，建立了54-5-5-1的双隐藏层神经网络，共有300个权值。将生成的数据选5 000组作为训练集进行训练，100组作为测试集。测试得到的期望输出和预测输出结果对比如图6所示。其中期望输出为100组布置方案的实际MAC值，预测输出为训练后的神经网络的预测结果值。

图6　神经网络预测输出对比

从图6可以看出，该网络的100组布置方案的预测输出和实际输出MAC值很接近，训练效果比较理想。为进一步分析整体预测效果，计算该神经网络的预测误差及误差百分比，如图7所示。

(a)神经网络预测误差

(b)神经网络预测误差百分比

从图7(a)可以看出，大多数误差均在±0.04范围内，少数误差达到0.06以上。从图7(b)可以看出，有个别误差相对较大，但大多数误差百分比都在0附近。总体来说，该网络基本满足精度要求。

在已训练好的网络上，采用遗传算法搜索该预测网络的最小值，初始化时设置迭代次数为200，种群规模为20，交叉概率选择0.4，变异概率选择0.2，经迭代运算后获得最优结果，为0.111 87，适应度变化曲线如图8所示，其对应54个点的布置方案及MAC矩阵最值和平均值如表2所示。

图8　适应度变化曲线

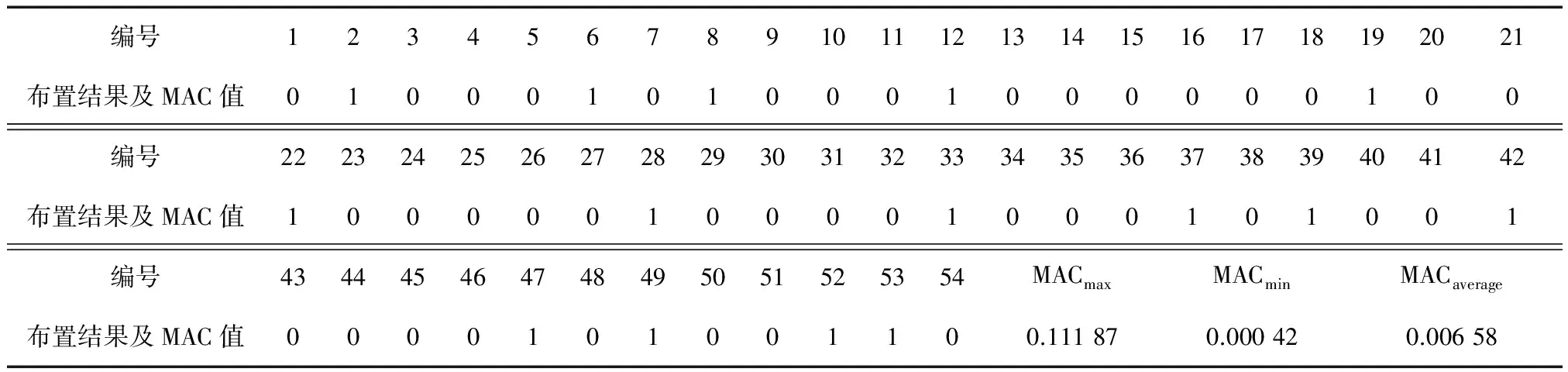
表2　布置方案结果

该布置方案对应的MAC矩阵如图9所示。

MAC矩阵的非对角元素的最大值为0.111 87，出现在y方向2阶和3阶之间，其余值均很小，说明各模态之间保留了较好的正交性，整体结果比较理想。这里采用三次插值拟合，得到前5阶y方向振型对比图，如图10所示。

从图10可以看出，该布置方案拟合的振型很接近实际振型(几乎重合)，能满足桥梁振动响应监测的要求。

6　总结与讨论

笔者利用神经网络建立布置方案和评价结果的映射关系，这种网络关系接近它们的实际映射关系，同时这个网络关系不复杂，这使遗传算法更容易寻优。实验结果表明，该方法是可行的且具有一定的实用价值。但是，传感器优化布置效果直接受神经网络训练效果影响，本文只证明了该方法有效，未与单独的遗传算法进行详细的对比。后面的研究可以从下面2方面进行。

图9　MAC矩阵

(a)1阶y方向振型对比　　　　　(b)2阶y方向振型对比

(c)3阶y方向振型对比　　　　　(d)4阶y方向振型对比

(e)5阶y方向振型对比

1)从隐含层层数及节点数量、参数初始化等方面改善神经网络，减小误差。

2)尝试与其他群智能算法结合，并与本文提出的方法进行对比分析。

[1]KAMMER D C, TINKER M L. Optimal placement of triaxial accelerometers for modal vibration tests[J]. Mechanical Systems and Signal Processing, 2004, 18(1)：:29．

[2]詹杰子, 余岭. 传感器优化布置的有效独立：改进模态应变能方法[J]. 振动与冲击, 2017, 36(1):82.

[3]KAMMER D C. Effect of model error on sensor placement for on-orbit modal identification of large space structures[J]. Journal of Guidance Control & Dynamics, 1992, 15(2):334.

[4]赵宇，殷红，彭珍瑞. 免疫算法在桥梁监测传感器优化配置中的应用[J]．兰州交通大学学报，2013,32(4):39．

[5]伊廷华，张旭东，李宏男．基于病毒猴群算法的传感器优化布置方法研究[J]．计算力学学报，2014, 31(3)：285．

[6]YI T H, ZHOU G D, LI H N, et al. Optimal sensor placement for health monitoring of high-rise structure based on collaborative-climb monkey algorithm[J]. Structural Control & Health Monitoring, 2015, 22(4):667.

[7]孙正华, 李兆霞,韩晓林,等. 大跨桥梁索塔环境振动测点布置研究[J].工程抗震与加固改造, 2006, 28 (3) :88.

[8]HAYKIN S.Neural Networks & Learning Machines[M]. Upper Saddle River：Pearson Education, 2009.

[9]高维成, 徐敏建, 刘伟. 基于遗传算法的传感器优化布置[J]. 哈尔滨工业大学学报, 2008, 40(1):9.