落石碰撞切向恢复系数的取值研究
叶四桥,巩尚卿,王林峰,谢 涛,王宗建
(1.重庆交通大学 岩土工程研究所,重庆 400074;2.重庆市地质矿产勘察开发局 博士后工作站,重庆 401121)
崩塌落石是我国山地三大地质灾害之一,其威胁区域即为落石运动轨迹所达范围,破坏能力取决于落石冲击动能和危害对象的易损性,所以,在实际工程中,获取落石运动轨迹、冲击动能及冲击力等参数是被动防护成功的基础,也是本领域研究中的关键和热点问题[1-2]。要通过落石运动计算软件或数值模拟得到相对客观的落石运动轨迹和运动参数,必须先有切向、法向恢复系数和滚动摩擦系数等的合理取值。根据文献[3—6]的研究,切向恢复系数受落石撞击边坡时的坡度(部分文献以入射角表示)、坡面物理状态和落石的质量、形状、碰撞时的入射速度等多种因素的影响。
为考察各影响因素对切向恢复系数的影响,国内外研究人员做了大量工作,所使用的研究手段主要有3种:理论分析、模型试验和现场试验。理论分析方面,杨海清等[7]将落石的形状概化为椭球,提出了切向恢复系数的计算公式;何思明等[8]基于接触理论推导了相应计算公式。模型试验方面,叶四桥等[9]、黄润秋等[10]通过试验获取碰撞前后落石的入射速度、反弹速度,并依据恢复系数的定义反算得到了法向恢复系数;Chau等[11]、Labiouse等[12]发现边坡坡面软硬状态、植被特征、坡度、落石形状、下落高度等均会影响切向恢复系数的取值;章广成[13]通过试验与数值模拟发现落石的边长对切向恢复系数几乎无影响,主要影响因素为入射角和入射速度,与入射角呈现反相关,与入射速度呈现正相关的变化特点。现场试验方面,Giani等[14]依据大比尺的现场实验,通过影像记录反分析试验条件下的切向碰撞恢复系数,并建议在0.3~0.85之间取值;Guzzetti等[15]为软件计算的需要提出切向恢复系数的建议取值为0.4~0.9。
总体来看,各机构的学者,各类分析软件在切向恢复系数的取值方面差异较大[9-17],且对切向恢复系数的取值往往只依据坡面软硬特征来分类,或辅以一定的工程经验性描述分类取值,客观上造成切向恢复系数取值随意性大,经验性较强。本文通过不同坡面状态、落石形状和质量的落石冲击试验,进行落石碰撞切向恢复系数的取值研究。
1 模型试验方案及数据处理
1.1 模型试验方案
落石冲击试验用落石试块采用C30混凝土浇筑,为考察落石形状和质量对切向恢复系数的影响,预制了圆球、立方体、长方体、圆柱体共4种形状的落石如图1所示。每种形状落石设置了5种不同质量,各试块的质量、形状及尺寸见表1。为便于在后期试验中用绳索吊起和释放试块,试块浇筑前在试块模板中预埋铁丝提扣。

图1 落石试件的形状

质量/kg圆球半径/mm立方体边长/mm长方体圆柱体长/mm宽/mm高/mm半径/mm柱高/mm3567580192969640408881001202561281287013011571101602801401408017016651251753201601601002002184135200350175175120240
为体现落石碰撞坡面坡度、坡面软硬及植被状态等对碰撞过程切向恢复系数的影响,将试验坡段设置为一块钢筋混凝土预制板搭设的单坡,通过改变混凝土板的倾角模拟不同的边坡坡度,坡面通过不同材质铺装模拟实际边坡的软硬物理状态。试验中,设置的坡度有15°,30°,45°和60°共4种,坡面铺装的具体工况见表2。以落石试块提升至规定高度模拟不同的碰撞速度,设定0.5,1.0,1.5和2.0 m共4级自由坠落高度。

表2 预制板表面铺装工况
为了实现高速相机捕捉落石的运动轨迹,在试件上粘贴物体识别片,注意要保证圆片中心点与高速相机拍摄的试件一面的中心位置重合,即以圆片的中心点重合试件的形心点如图2所示。

图2 粘贴物体识别片的试验落石
试验时,按预定工况设定好试验坡面后,运用试验塔架提升系统提升试验落石至预定高度,释放落石试块,使其自由下落冲击试验坡面,同时使用MotionXtra HG-100K型高速相机以1 000帧·s-1的速度拍摄落石试块碰撞坡面的照片集。
1.2 试验数据处理

按切向恢复系数定义
(1)
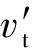
将获得的水平方向、竖直方向的入射速度、反弹速度沿边坡面切向方向分解,由几何关系可得
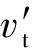
(2)
vt=vVsinα
(3)
式中:α为斜坡坡度,(°)。
从调查结果我们可以看到,部分教师素质能力的缺乏也是造成旅游英语专业跨文化交际能力较低的原因之一,因此,除了进行有效的教学设计之外,还应采取有效措施对旅游英语专业教师队伍的综合文化知识的素质及跨文化交际能力进行提升,为旅游英语专业学生跨文化交际能力的提高奠定坚实的基础和条件;其次,学校还应从师资队伍的合理化配置、科学化、国际化构成实际出发,聘用一定的外教人员,为学生学习纯正的国际语言学习创造国际化的环境和国际化的文化氛围。[5]
则有
(4)
基于每次成功拍摄获得的1组照片集,由式(1)—式(4)即可得该次落石碰撞试验的切向恢复系数。按以上试验方案,本次试验成功获取了1 600个不同情形下的切向恢复系数。
2 切向恢复系数影响因素分析
由于试验获得的数据样本大,且所得的切向恢复系数分布离散程度较高,为揭示切向恢复系数随落石形状、质量、坡面物理状态等影响因素的变化规律,对各影响因素进行了单因素分析。
2.1 坡面物理状态
图3给出了试验得到的不同坡面物理状态下切向恢复系数最大值、平均值和最小值的变化曲线。从图3可以看出:随坡面铺装从河沙、土层、草皮、木板到光面,即由软到硬变化,切向恢复系数的最大值、最小值以及平均值均逐渐增大,特别是平均值的增幅明显,变化范围为0.66~0.84,说明边坡坡面岩土层越坚硬,切向恢复系数越大,边坡坡面越松软,切向恢复系数越小。试验所得结果反映的规律同目前有关指南、软件中的取值规律是一致的[4-15]。

图3 不同坡面物理状态下的切向恢复系数曲线
需要特别指出的是,不论坡面软硬程度如何,从切向恢复系数随机变化区间来看,其离散性极大,最软河沙坡面的变化区间为0.20~0.92,最硬的光面坡面的变化区间为0.25~0.96,说明落石实际运动路径计算中,对切向恢复系数采用区间随机取值应更符合实际。
图4给出了不同坡面铺装下切向恢复系数在0~1分布区间各区段的分布情况,由图4可以看出:
(1)0.2以下没有试验数据分布,且93%以上的切向恢复系数数据分布在0.5以上的区间,0.4以上的占总试验次数的98%,表明无论坡面软硬程度如何,工程中切向恢复系数取0.5以上是符合实际且偏于安全的。换言之,目前有关取值甚至有取到0.4以下,甚至0.3的,取值偏小会导致计算所得运动动能偏小,进而使被动防护结构设计安全储备不足。
(2)在0.4—0.5,0.5—0.6和0.6—0.7取值区间上,河沙和土层工况下的数据较多,在此3个区间上河沙铺装占43.7%,土层占34.1%;而在0.8—0.9和0.9—1.0较大的取值区间上,坡面越硬,数据占比越多,如木板占54.7%,光面占52.5%。总体来看,取值区间越大,切向恢复系数在此区间的数据量越多。

图4 不同坡面物理状态下切向恢复系数在各取值区间的分布
2.2 坡度
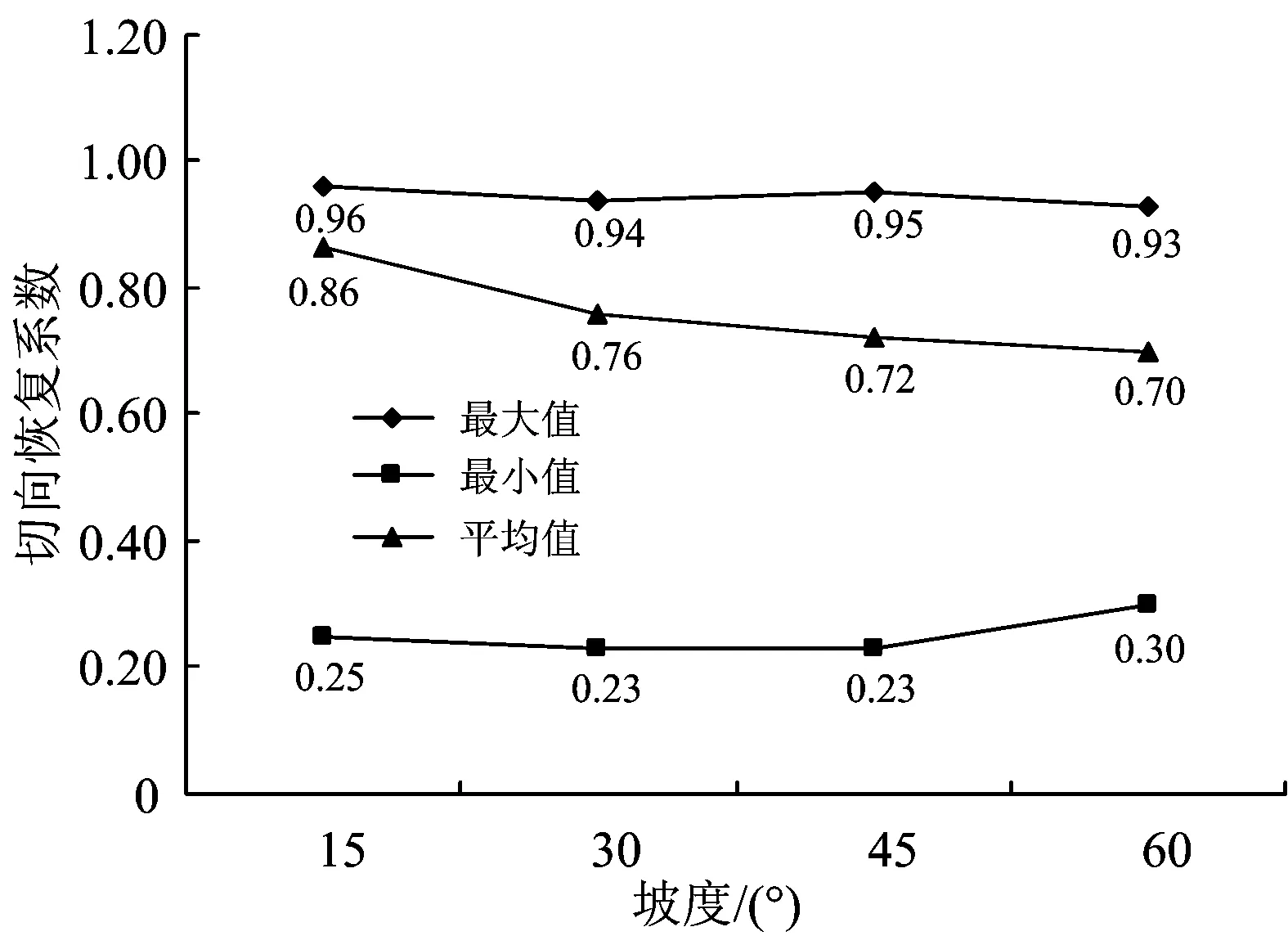
图5 不同坡面坡度下切向恢复系数曲线
在4种坡度下,切向恢复系数在各区间上的分布如图6所示。从图6可以看出:
(1)在较小的前5个小区间内,切向恢复系数个数较少且分布散乱,而在较大的后3个小区间内,数据分布较多,在0.9~1.0最大区间内, 15°边坡条件下切向恢复系数分布个数最多,占此区间的58%,也从侧面证明了碰撞坡面坡度小时切向恢复系数越大的规律。
(2)随着取值区间的增大,切向恢复系数的个数有越来越多的趋势。

图6 不同坡面坡度下切向恢复系数在各取值区间的分布
2.3 落石形状
图7为4种落石形状下切向恢复系数最大值、平均值和最小值的变化曲线。由图7可以看出:4种落石形状下,切向恢复系数最大值和平均值无显著区别,而对于切向恢复系数最小值,除去立方体试件稍大外,圆球、长方体和圆柱体试件也无显著区别。由此可以推断,不管何种形状的落石,各种试验条件下得到的切向恢复系数数值无明显差别,在实际工程中可不考虑落石形状对切向恢复系数取值的影响。
图8给出了不同形状落石切向恢复系数在各取值区间的分布情况。由图8可以看出:在各取值区间内4种形状落石的切向恢复系数数据个数没有明显差异,即形状因素对恢复系数取值的影响不明显;切向恢复系数的个数随着取值区间增大而增多。
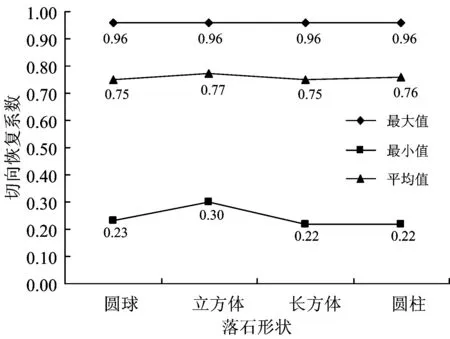
图7 不同落石形状的切向恢复系数曲线
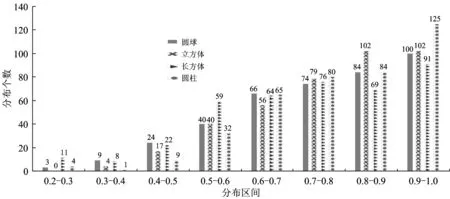
图8 不同形状落石切向恢复系数在各取值区间的分布
2.4 下落高度
下落高度即落石入射速度的影响。图9给出了4种下落高度情形下切向恢复系数最大值、平均值和最小值的变化曲线。从图9可以看出:下落高度越大(入射速度越大),所得切向恢复系数平均值和最小值有逐渐减小的趋势,下落高度从0.5 m增加到2 m,切向恢复系数平均值减小幅度约14%。由于速度增加导致切向恢复系数减小的特性对落石运动计算而言是偏安全的,实际工程中可以不考虑下落高度,即不考虑入射速度对切向恢复系数取值的影响。

图9 不同下落高度情况下切向恢复系数曲线
图10是不同下落高度下切向恢复系数在各取值区间的分布情况。从图10可以看出:在各区间4种下落高度下的切向恢复系数个数较为一致;在几乎所有区间内,4种下落高度情形下分布个数相差不多,0.9—1.0区间0.5 m下落高度下切向恢复系数分布最多,占此区间总数的33%;随着取值区间的增大,切向恢复系数的个数越来越多。

图10 不同下落高度情况下切向恢复系数在各取值区间的分布
2.5 落石质量
图11给出了5种质量落石的切向恢复系数最大值、平均值和最小值的变化曲线。由图11可以看出:随落石质量的增大,切向恢复系数逐渐增大;随落石质量增大,切向恢复系数平均值增大幅度约20%。落石运动计算中如果不考虑落石质量增大导致切向恢复系数增大的特性,则是偏危险的,所以实际工程中有必要计入质量对切向恢复系数的影响。
图12揭示了不同落石质量下切向恢复系数在各区间上的分布特征。由图12可见:0.4~0.5,0.5~0.6和0.6~0.7区间内,小质量落石对应切向恢复系数分布较多,在0.8~0.9和0.9~1.0区间内,对应的落石质量也大;数值上越大的区间,切向恢复系数分布的个数也越多。

图11 不同质量落石切向恢复系数曲线

图12 不同质量落石切向恢复系数在各取值区间的分布
3 切向恢复系数取值建议
本领域学者普遍认为坡面物理状态对切向恢复系数的影响大,因此多以边坡坡面的性状不同设定切向恢复系数的取值。通行的做法是先对边坡坡面覆盖物的软硬程度作定性描述,然后列出对应于坡面不同物理状态的取值表,或给出单值。如Chau等建议土质坡面取0.567,混凝土铺砌坡面取0.737,基岩坡面取0.910;而Hoek等则建议对土质坡面取0.8,基岩坡面取0.99。总体来看,各研究人员取值方法和取值建议有比较大的差别[4-15],也均未能反映边坡坡度、落石自身因素及下落高度(入射速度)等敏感因素对切向恢复系数取值的影响。
研究表明,显著影响切向恢复系数的因素有4个:坡面软硬状态、边坡坡度、落石质量和入射速度。有影响的4个因素中下落高度越大,切向恢复系数反而越小,该特性对于实际落石运动计算而言是偏安全的,故可以不考虑入射速度的影响;试验表明,切向恢复系数有随着落石的质量增大而增大的特征,但考虑到本文试验所涉及的质量区间有限,且总体而言质量区间较小,无法确定落石质量对切向恢复系数取值的确切影响。坡表软硬状态和边坡坡度可以通过野外调查确定,且确有显著影响,为便于应用,建议将切向恢复系数取值区间按坡面软硬状态和落石可能滚落的边坡坡度进行划分。划分原则为取值区间能够覆盖95%的试验数据,并能够客观反映边坡坡度和坡面软硬状态对切向恢复系数的影响,取值建议见表3。
在实际选用时,碰撞发生的坡面越硬、坡度越小、落石质量越大时建议取区间内高值,反之则偏于区间低值取值。对于可以实现随机取值的落石运动计算软件或类似算法,则可直接选用以上区间随机取值。

表3 切向恢复系数取值建议表
4 结 论
(1)坡面铺装、坡度、落石质量、下落高度对切向恢复系数均有明显影响,落石形状则无明显影响。随着碰撞坡面由软到硬,边坡坡度的减小,落石质量的增大,下落高度的减小,切向恢复系数逐渐增大;反之,则逐渐减小。
(2)切向恢复系数大多在0.4以上,占总试验次数的98%,0.5以上的占93%,而0.9以上的占25%。可见在落石碰撞坡面过程中,落石切向速度折减有限,速度损失主要发生在碰撞的法向方向。另外,目前工程界采用的切向恢复系数取值在部分情形下偏小,可能导致被动防护设计安全储备不足。
(3)给出了切向恢复系数建议取值表,在实际使用时,应根据现场坡面物理状态和边坡坡度综合取值,并建议坡面越松软,边坡坡度越大,偏于区间低值;反之,偏于区间高值,或直接采用区间随机取值。
(4)对于质量对落石碰撞切向恢复系数取值的影响,以及不同初始下落角度,边、角碰撞坡表的情形,仍需要进一步的研究和数据支持。
[1]叶阳升,蔡德钩,闫宏业,等.激振作用下坠落式危岩振动特性试验研究[J].中国铁道科学,2015,36(6):16-21.
(YE Yangsheng,CAI Degou,YAN Hongye,et al.Experimental Study on Vibration Characteristics of Falling Unstable Rock under Excitation[J].China Railway Science, 2015,36(6):16-21.in Chinese)
[2]王林峰,唐红梅,陈洪凯.消能棚洞的落石冲击计算及消能效果研究[J]. 中国铁道科学,2012,33(5):40-46.
(WANG Linfeng, TANG Hongmei, CHEN Hongkai.Study on the Calculation Method for Rockfall Impact and Energy Dissipation Effect of Energy Dissipation Shed Tunnel[J].China Railway Science, 2012,33(5):40-46.in Chinese)
[3]BOZZOLO D, PAMINI B. Simulation of Rock Falls down a Valley Side[J]. ACTA Mechanica,1986,63: 113-130.
[4]AZZONI A, BARBERA G, ZANINETTI A. Analysis and Prediction of Rockfalls Using a Mathematical Model[J]. International Journal of Rock Mechanics and Mining Sciences,1995, 32(7):709-724.
[5]BOURRIER F, DORREN L, NICOT F, et al. Toward Objective Rockfall Trajectory Simulation Using a Stochastic Impact Model[J]. Geomorphology,2009,110:68-79.
[6]AZZONI A, FREITAS M. Experimentally Gained Parameters,Decisive for Rockfall Analysis[J]. Rock Mechanics and Rock Engineering,1995,28(2):111-124.
[7]杨海清,周小平.边坡落石运动轨迹计算新方法[J].岩土力学,2009,30(11):3411-3417.
(YANG Haiqing, ZHOU Xiaoping. A New Approach to Calculate Trajectory of Rockfall[J].Rock and Soil Mechanics,2009,30(11):3411-3417. in Chinese)
[8]何思明,吴永,李新坡.滚石冲击碰撞恢复系数研究[J].岩土力学,2009,30(3):623-627.
(HE Siming,WU Yong, LI Xinpo. Research on Restitution Coefficient of Rock Fall[J].Rock and Soil Mechanics, 2009,30(3):623-627. in Chinese)
[9]叶四桥,巩尚卿.落石碰撞法向恢复系数的模型试验研究[J].中国铁道科学,2015,36(4):13-17.
(YE Siqiao, GONG Shangqing. Research on Normal Restitution Coefficient of Rockfall Collision by Model Tests[J].China Railway Science, 2015,36(4):13-17.in Chinese)
[10]黄润秋,刘卫华.平台对滚石停积作用试验研究[J].岩石力学与工程学报,2009,28(3):516-524.
(HUANG Runqiu, LIU Weihua. Platform Resistant Test on Rolling Rock Blocks[J]. Chinese Journal of Rock Mechanics and Engineering, 2009,28(3):516-524.in Chinese)
[11]CHAU K T, WONG R H C, WU J J. Coefficient of Restitution and Rotational Motions of Rockfall Impacts[J]. International Journal of Rock Mechanics and Mining Sciences,2002, 39:69-77.
[12]LABIOUSE V,HEIDENREICH B. Half-Scale Experimental Study of Rockfall Impacts on Sandy Slopes[J].Natural Hazards and Earth System Sciences, 2009(9):1981-1993.
[13]章广成,向欣,唐辉明.落石碰撞恢复系数的现场试验与数值计算[J].岩石力学与工程学报,2011,30(6):1266-1273.
(ZHANG Guangcheng, XIANG Xin,TANG Huiming. Field Test and Numerical Calculation of Restitution Coefficient of Rockfall Collision[J].Chinese Journal of Rock Mechanics and Engineering, 2011,30(6):1266-1273. in Chinese)
[14]GIANI G P, GIACOMINI A, MIGLIAZZA M, et al. Experimental and Theoretical Studies to Improve Rockfall Analysis and Protection Work Design[J]. Rock Mechanics and Rock Engineering. 2004,37 (5):369-389.
[15]FAUSTO Guzzetti, GIOVANNI Crosta, RICCARDO Detti, et al. STONE: a Computer Program for the Three-Dimensional Simulation of Rock-Falls [J]. Computers & Geosciences, 2002, 28(9): 1079-1093.
[16]向欣.边坡落石运动特性及碰撞冲击作用研究[D].武汉:中国地质大学,2010:1-17.
(XIANG Xin. Research on Motion Characteristics and Impact Force of Rockfall[D].Wuhan: China University of Geosciences, 2010:1-17.in Chinese)
[17]贺咏梅.高陡岩质斜坡崩落岩体运动参数、击浪高度及其对工程影响研究[D].成都:成都理工大学.2011:5-23.
(HE Yongmei. Motion Parameters and Striking Surge of Rockfall from High-Steep Rocky Slopes and Its Engineering Effects [D].Chengdu: Chengdu University of Technology, 2011:5-23.in Chinese)

