高速铁路车站列车进路分配方案的优化与调整
马 驷,孙建康,鲁工圆
(1.西南交通大学 交通运输与物流学院,四川 成都 610031;2.西南交通大学 综合交通运输智能化国家地方联合工程实验室,四川 成都 610031)
高速铁路车站列车进路分配是车站作业计划的关键工作,也是维持运输网络稳定和高效的决定性因素。国外学者往往将经过简化和抽象的列车进路排序模型应用于车站作业计划自动化编制和动态调整工作当中。在列车进路分配模型构建方面,Zwaneveld等[1-2]和Kroon等[3]分别从不同的角度考虑列车进路排序问题,并抽象为节点封装问题,建立了该问题的整数规划模型;Lusby等[4]以车站的可行进路数最大化为主要目标,将列车在车站的可行进路排列问题抽象为加权的节点压缩模型,并应用分枝定界方法求解,该模型可以处理许多大规模的进路。在列车进路分配方案调整方面,D’Ariano等[5]和Caprara等[6]考虑随机扰动情况,深入研究列车进路分配方案调整方法;Chakroborty等[7]设定列车到达车站的最终时间点在列车到达车站前一段时间才能够确定,通过产生列车延误达到列车到发线分配方案动态调整的目的;Corman等[8]针对铁路车站实际运营中出现突发事件的情况,以最小化列车延误时间为优化目标,通过调整列车停站时间、列车速度、进站顺序及进路分配等,实现车站作业计划的动态调整。但以上这些研究对咽喉区和到发线的制约关系考虑较少。当然,部分学者在对铁路通过能力的研究中探讨了车站设备的运用关系,对理清咽喉区和到发线之间的关系具有一定的参考意义[9]。
我国高速铁路车站采用平面布局形式,咽喉区结构复杂,列车进路交叉干扰大,对于列车进路分配问题的研究重点围绕咽喉区和到发线展开。刘澜等[10]将咽喉区线路抽象成1个多源多汇的网络,建立车站咽喉作业占用安排网络优化和咽喉作业能力复合递阶决策模型,并实现计算机运算;史峰等[11]通过构建咽喉区的有向网络对咽喉区的进路进行优化;吕颖等[12]提出了具有普适性的高速铁路车站到发线优化运用非线性规划模型;王保山等[13]研究了以利于乘降作业和均衡使用车站设备为指标的到发线运用多目标优化模型。但是,文献[10—11]中,单纯的咽喉区网络化研究未充分考虑多项作业同时进行时,到发线对咽喉网络占用的制约性,难以应用于实践;文献[12—13]中,单纯的到发线运用优化研究仅仅针对的是列车占用到发线,未考虑咽喉区使用的合理性。
基于以上分析,建立咽喉区和到发线一体化运用模型至关重要,相关研究也逐渐跟进,如赵鹏等[14]建立到发线和咽喉区综合优化模型,运用模拟退火算法求解,但模型对部分作业过程进行了简化处理。总体来说,这种咽喉区和到发线的一体化研究尚不成熟。
本文依据高速铁路车站平面图和列车运行图,考虑咽喉区和到发线的连通性、车站设备的运用,以及各种类型列车的车站作业过程与列车进路的关系,结合道岔分组的方法,建立咽喉区和到发线一体化运用的列车进路分配方案优化模型及其动态调整模型,采用运筹学软件LINGO中内置的分支定界算法求解,得到高速铁路车站列车进路分配的优化方案和动态调整方案。
1 车站作业过程与列车进路关系
列车进路是指列车在车站到、发、通过、折返、动车出入段过程中占用的车站内部一段线路。部分学者认为“当列车通过咽喉区的进路确定后,到发线也随之确定”[15-16],这里的“进路”指的就是列车进路。车站作业过程与列车进路是一一对应的,不同种类列车的车站作业过程与列车进路的对应关系见表1。

表1 不同种类列车车站作业过程与列车进路对应关系
从车站设备角度考虑,列车进路包括过咽喉区径路和到发线两部分。
(1)过咽喉区径路。过咽喉区径路由若干道岔组组成,以图1为例对过咽喉区径路进行简要分析。办理接车作业可以占用的过咽喉区径路为①→②,①→③,办理站前折返作业可以占用的过咽喉区径路为②→①→④,③→④;由于①→②,①→③,②→①→④这3条径路共用道岔组①,故这3条径路相互干扰,不可同时被占用;②→①→④和③→④这2条径路共用道岔组④,故这2条径路亦相互干扰,不可同时被占用;①→②和③→④这2条径路不存在共用道岔组,故这2条径路不相互干扰,可以同时被占用;此外,同一过咽喉区径路占用的道岔组完全一致,亦可视为相互干扰、不可同时被2个车站作业过程占用;依据这样的原则,可逐步理清整个车站所有过咽喉区径路之间的关系。
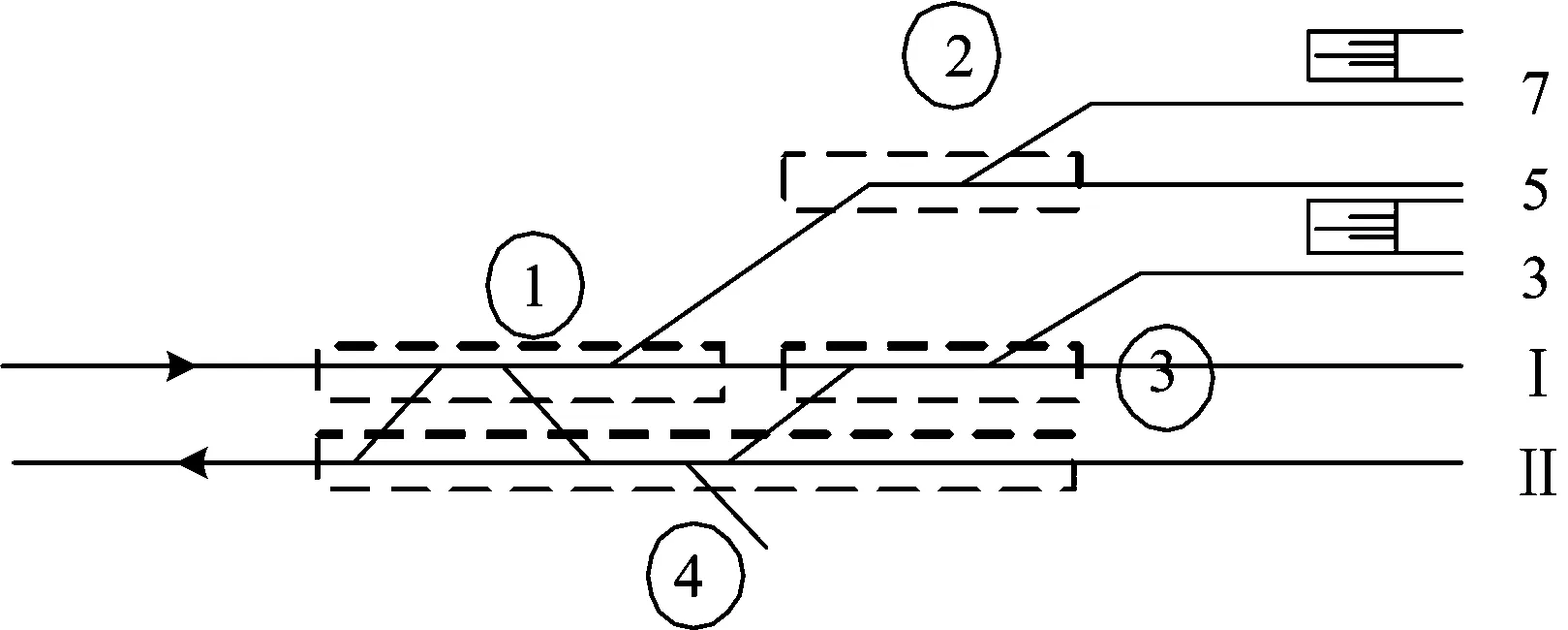
图1 某车站一端部分咽喉区道岔分组图
(2)到发线。到发线之间相互独立,1个车站作业过程只能占用1条到发线,相邻2个车站作业过程占用同一条到发线,则需满足到发线使用最小间隔时间的要求。
过咽喉区径路和到发线之间的关系可表述为:1条过咽喉区径路通常连接多条到发线;列车到达固定到发线往往有多条过咽喉区径路可以选择;二者相互联系、相互制约。
基于以上分析,本文的研究重点是在咽喉区和到发线一体化运用的基础上,通过建立列车进路分配方案的优化模型和动态调整模型,确定某一时段从第1个车站作业过程开始占用车站设备时起至最后1个车站作业过程清空车站设备时止列车占用咽喉区和到发线的时序排列方案。
2 列车进路分配方案优化模型的建立
2.1 模型假设
(1)已知高速铁路车站站场布置、到发线固定使用方案、列车种类及到发时刻。
(2)列车严格按照高速铁路车站各项时间标准进行作业。
(3)不考虑轨道电路的分段解锁,通过道岔分组表达列车进路间的逻辑关系。
2.2 变量及参数说明
P为车站在某时段接发所有列车的集合,按照列车开始占用车站设备的时刻进行排序,记P={1,…,p,…,W},其中W为列车总数,对于同时占用车站设备的不同列车,任取其1个优先排序;I为车站在该时段办理所有车站作业过程的集合,根据其开始占用车站设备的时刻对车站作业过程进行排序,记I={1,…,ip,…,hp+q,…,M},其中q为整数,M为车站作业过程总数,对于同时占用车站设备的不同车站作业过程,任取其1个优先排序;在已知列车运行图的前提下,车站作业过程序号与列车序号均可推知且相互对应,这里将列车序号p作为车站作业过程序号ip的一项属性。J为车站可用于接发列车的所有到发线集合,记J={1,…,j,…,m},其中m为到发线数量。K为车站接发列车的过咽喉区径路集合,记K={1,…,k,…,k′,…,n},其中n为过咽喉区径路数量。U为车站咽喉区道岔组集合,记U={1,…,u,…,v},其中v为咽喉区道岔组总数量。
(1)定义以下参量描述列车占用车站设备的时间状况。
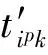
(2)定义以下0-1参量描述车站设备关系及到发线固定使用方案。
akj表示过咽喉区径路与到发线之间的连通性关系,若过咽喉区径路k与到发线j直接连通,则akj=1,否则akj=0;则有过咽喉区径路和到发线的连通性矩阵An×m。bkk′表示过咽喉区径路之间的关系,若2条过咽喉区径路k与k′相互干扰,则bkk′=1,否则bkk′=0;则有各过咽喉区径路之间的关系矩阵Bn×n。cipj表示车站作业过程ip可占用的到发线状况,若车站作业过程ip可以占用到发线j,则cipj=1,否则cipj=0;则有车站作业过程可占用的到发线矩阵CM×m。dipk表示车站作业过程ip可占用的过咽喉区径路状况,若车站作业过程ip可以占用过咽喉区径路k,则dipk=1,否则dipk=0;则有车站作业过程可占用的过咽喉区径路矩阵DM×n。eku表示过咽喉区径路与道岔组之间的关系,若过咽喉区径路k包含道岔组u,则eku=1,否则eku=0;则有过咽喉区径路与道岔组关系矩阵En×v。δrs为克罗内克尔符号,若r=s,则δrs=1;否则δrs=0。
(3)定义如下0-1决策变量,描述车站作业过程与过咽喉区径路、到发线的关系。
2.3 列车进路分配方案优化模型
从设备利用率的角度考虑,为减少出现部分设备能力紧张而部分设备能力空费的情况,同类设备应均衡运用;从车站作业计划质量的角度考虑,列车进路分配方案中到发线被占用的均衡性越强,其抗干扰能力往往越强[17]。因此,以车站作业过程占用到发线不均衡性最小为优化目标1,采用各到发线被占用时间的方差表示该不均衡性,即
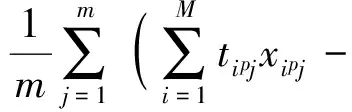
(1)
以车站作业过程占用咽喉区道岔组的不均衡性最小作为优化目标2,并采用各道岔组被占用时间的方差表示该不均衡性,即

(2)
采用线性加权求和的方法,将多目标转化为单目标,得到列车进路分配方案优化模型M1,即
minZ3=λ1Z1+λ2Z2
(3)
s.t.
(4)
(5)
(6)
xipj=cipjxipjip∈I;j∈J
(7)
yipk=dipkyipkip∈I;k∈K
(8)
δp(p+q)xipj=δp(p+q)xhp+qjip,hp+q∈I;j∈J
(9)
(1-δp(p+q))xhp+qjT1
ip,hp+q∈I且ip (10) bkk′yhp+qk′T2 ip,hp+q∈I且ip (11) (12) 目标函数式(3)中,λ1和λ2分别为目标函数Z1和Z2的权重。约束条件中:式(4)表示1个车站作业过程占用过咽喉区径路和到发线有唯一方案;式(5)表示列车进路确定以后,到发线唯一确定;式(6)表示列车进路确定以后,过咽喉区径路唯一确定;式(7)表示任意1个车站作业过程仅在其可以占用的到发线或正线上办理;式(8)表示任一车站作业过程仅在其可以占用的过咽喉区径路上办理;式(9)表示同一方向、同一列车的不同车站作业过程必然占用同一条到发线;式(10)表示占用同一到发线的不同列车的前后2个车站作业过程之间的时间间隔必须不小于到发线安全使用间隔时间;式(11)表示占用2条相互干扰的过咽喉区径路的前后2个车站作业过程之间的间隔时间必须不小于过咽喉区径路安全使用间隔时间。 定义集合Ωip={(j,k)|j=j*,k=k*},表示模型M1所得的优化结果中车站作业过程ip的列车进路分配方案,该方案包含车站作业过程ip占用到发线j和过咽喉区径路k的序号信息。引入决策变量Δtip,表示疏解列车进路的过程中车站作业过程ip产生的延误时间。当某列车发生意外晚点,需为后续列车提供实时更新的列车进路分配方案,以保证车站接发车作业的流畅性。此外,由于允许后续列车发生延误,后续车站作业过程占用同类车站设备的选择性会更多,车站设备运用均衡性的可优化空间可能会进一步增大。以车站作业过程占用车站设备的不均衡性最小[模型M1中目标函数式(3)]和车站作业过程平均延误时间最少为目标函数,建立后续列车进路分配方案的动态调整模型M2,即 模型M1中的目标函数式(3) (13) s.t. 模型M1中的式(4)—式(9)和式(12)。 模型M1中的式(10)和式(11)需考虑车站作业过程延误时间,转化为以下2个公式。 (1-δp(p+q))xhp+qjT1 ip,hp+q∈I且ip (14) ip,hp+q∈I且ip (15) 这里要求列车严格按照时间标准作业,则同一列车包含的不同车站作业过程的延误时间一致,即 δp(p+q)Δtip=δp(p+q)Δthp+qip,hp+q∈I (16) 车站作业过程延误时间属于自然数集合Ν,且为避免个别列车过度延误,需设定列车延误时间的上限τ,则有 (17) Δtip≤τip∈I (18) (19) 分析所建立的模型M1和模型M2可知:2个模型均为非线性整数规划模型,且目标函数中的式(3)和式(13)均为或可视为凸函数,不等式约束条件中的式(10)、式(11)、式(14)、式(15)、式(18)均为或可视为凹函数,等式约束条件中的式(4)—式(9)、式(16)—式(18)均为线性函数,因此2个模型均为凸非线性整数规划模型。针对这一模型,本文运用LINGO软件中内置的分支定界算法对模型加以求解,在提高求解效率的前提下寻求得到全局最优解。 在求解模型M2过程中,考虑到有2个量纲不一致的目标函数,而LINGO无法直接求解多目标规划模型。由于这里需要优先保证后续车站作业过程占用设备的不均衡性最小,因此采取分层序列法将多目标规划模型转化为分层的单目标规划模型求解,即首先在不考虑目标函数式(13)的前提下,将目标函数式(3)作为唯一目标,求出最优值,然后将此最优值作为约束条件,再求解目标函数式(13)的最优值,从而得到最优解。 以某高速铁路车站A为例,采用本文提出的方法为该站高峰时段13对列车制定列车进路分配方案。对车站A两端咽喉区进行道岔分组,得到如图2所示车站平面图。 图2 高速铁路车站A平面图 图2中:Ⅰ,3,5,7道接发下行列车;Ⅱ,4,6,8道接发上行列车;正线Ⅰ、Ⅱ两侧无站台,只接发上、下行不停站通过列车;①,②,…,为咽喉区道岔组。 车站A在18:00—19:40客流高峰时段办理的上、下行方向列车种类及到发时刻见表2。 采用CTCS-3级列车运行控制系统关于300 km·h-1等级高速列车车站技术作业时间标准[18],见表3。对于通过列车,占用1个通过进路和1条正线,总的时间为3 min。取到发线安全使用间隔时间为2 min,过咽喉区径路安全使用间隔时间为1 min。 结合列车到发时刻表,推算车站作业过程序号与列车序号的一一对应关系,见表4。 表2 18:00—19:40时段车站A接发列车时刻表 表3 各种类型列车所对应车站作业过程占用咽喉区和到发线的时间标准 min 表4 车站作业过程序号与列车序号间的对应关系表 根据车站咽喉区和到发线布置图,剔除无必要过咽喉区径路,得到车站可行列车进路,见表5。 基于以上分析,可得到描述车站设备关系及到发线固定使用方案的矩阵关系:过咽喉区径路和到发线的连通性矩阵A22×8;各过咽喉区径路之间的关系矩阵B22×22;车站作业过程可占用的到发线矩阵C46×8;车站作业过程可占用的过咽喉区径路矩阵D46×22;过咽喉区径路与道岔组之间的关系矩阵E22×14。 表5 车站列车进路表 以上参数确定之后,在CPU为Intel(R) Core(TM) i5-2430M 2.4GHz、内存为4G的电脑上,采用LINGO软件在较短时间内实现对模型M1和模型M2的求解。 (1)情况1:列车按照运行图正点进出车站,无列车意外晚点。 进一步分析模型M1的优化结果可知,各到发线被占用时间的方差为340.86,各道岔组被占用时间的方差为69.09。 (2)情况2:列车G9次意外晚点4 min,不能够按照运行图时刻表正点进出车站。 图3 无列车意外晚点情况下到发线占用方案 结合情况1中模型M1的求解结果,在列车G9次之前的列车进路分配方案不变的前提下,列车延误时间的上限τ取5 min,采用模型M2对后续车站作业过程的起止时刻进行调整。 表6 无列车意外晚点情况下列车进路分配方案 表7 列车G9次晚点4 min情况下列车进路分配方案 注:列车编号后的括号表示列车延误时间,无括号表示列车正点运行。 图4 列车G9次晚点4 min情况下到发线占用方案 进一步分析模型M2的优化结果可知,各到发线被占用时间的方差为310.61,各道岔组被占用时间的方差为69.09。该列车进路分配方案与情况1中模型M1所解得的方案相比,虽然道岔组使用均衡性没有进一步优化,但是到发线被占用时间的方差由340.86减少到了310.61,即到发线使用均衡性提高了8.87%,而车站作业过程平均延误时间由0 min增加到了1.61 min。 本文分析了高速铁路车站各种类型列车的车站作业过程和列车进路,建立了咽喉区和到发线一体化运用的列车进路分配方案优化模型及其动态调整模型。前者应用于车站列车进路分配方案的制定过程,可有效保证列车按照运行图进出站;但当出现列车意外晚点时,原列车进路分配方案中可能出现列车进路交叉干扰的情况;此时应采用后者对后续列车的进路分配方案进行调整,在保证后续列车延误时间控制在一定范围之内的条件下,实时更新列车进路分配方案,以有效保证列车进路的畅通,并使车站设备运用均衡性更优。本文暂未考虑这部分列车延误对车站技术作业和客运作业协调性的影响,该问题将在下一步工作中继续研究。 [1]ZWANEVELD P J, KROON L G, HOESEL S P M V. Routing Trains through a Railway Station Based on a Node Packing Model[J]. European Journal of Operational Research, 2001,128(1):14-33. [2]ZWANEVELD P J, KROON L G, ROMEIJN E, et al. Routing Trains through Railway Stations Model Formulation and Algorithms [J]. Transportation Science, 1996, 30 (3) :181-194. [3]KROON L G, ROMEIJN H E, ZWANEVELD P J. Routing Trains through Railway Stations: Complexity Issues[J]. European Journal of Operational Research, 1997, 98(3):485-498. [4]LUSBY R, LARSEN J, RYAN D, et al. Routing Trains through Railway Junctions: a New Set-Packing Approach[J]. Transportation Science, 2011, 45(2):228-245. [5]D’ARIANO A, CORMAN F, PACCIARELLI D, et al. Reordering and Local Rerouting Strategies to Manage Train Traffic in Real Time[J]. Transportation Science, 2008, 42(4):405-419. [6]CAPRARA A, GALLI L, TOTH P. Solution of the Train Platforming Problem[J]. Transportation Science, 2011, 45(2):246-257. [7]CHAKROBORTY P, VIKRAM D. Optimum Assignment of Trains to Platforms under Partial Schedule Compliance[J]. Transportation Research Part B:Methodological, 2008,42(2):169-184. [8]CORMAN F, D ARIANO A, PACCIARELLI D, et al. A Tabu Search Algorithm for Rerouting Trains during Rail Operations [J]. Transportation Research Part B: Methodological, 2010,44(1):175-192. [9]JAVADIAN N, SAYARSHAD H R, NAJAFI S. Using Simulated Annealing for Determination of the Capacity of Yard Stations in a Railway Industry[J]. Applied Soft Computing, 2011, 11(2):1899-1907. [10]刘澜,王南,杜文. 车站咽喉通过能力网络优化模型及算法研究[J]. 铁道学报, 2002, 24(6):1-5. (LIU Lan, WANG Nan, DU Wen. A Study of Network Optimization Model and Algorithm for Carrying Capacity of Station Throat[J]. Journal of the China Railway Society, 2002, 24(6):1-5. in Chinese) [11]史峰,谢楚农,于桂芳. 铁路车站咽喉区进路排列优化方法[J]. 铁道学报, 2004,26(4):5-9. (SHI Feng,XIE Chunong, YU Guifang. Optimization Methods for Arranging Train Routes in Station Bottleneck[J]. Journal of the China Railway Society, 2004, 26(4):5-9. in Chinese) [12]吕颖,马驷,王琳. 关于高速铁路车站到发线运用优化研究[J]. 铁道运输与经济, 2014, 36(8):26-31. (LÜ Ying, MA Si, WANG Lin. Study on Optimization of Arrival-Departure Line Using for High-Speed Railway Stations[J] . Railway Transport and Economy, 2014, 36(8):26-31. in Chinese) [13]王保山, 侯立新, 刘海东. 客运专线车站到发线运用优化方法[J]. 交通运输系统工程与信息, 2012, 12(2):105-110. (WANG Baoshan, HOU Lixin, LIU Haidong. Optimized Utilization of Arrival and Departure Tracks in Dedicated Passenger Lines[J]. Journal of Transportation Systems Engineering and Information Technology, 2012, 12(2):105-110. in Chinese) [14]赵鹏, 宋文波, 陈霞,等. 大型铁路客运站到发线与咽喉区综合运用优化[J]. 北京交通大学学报, 2015, 39(6):1-7. (ZHAO Peng, SONG Wenbo, CHEN Xia, et al. Comprehensive Optimization for Utilization of Arrival-Departure Tracks and Throat Area in Large Railway Passenger Station[J]. Journal of Beijing Jiaotong University, 2015, 39(6):1-7. in Chinese) [15]史峰, 陈彦, 秦进,等. 铁路客运站到发线运用和接发车进路排列方案综合优化[J]. 中国铁道科学, 2009, 30(6):108-113. (SHI Feng, CHEN Yan, QIN Jin, et al. Comprehensive Optimization of Arrival-Departure Track Utilization and Inbound-Outbound Route Assignment in Railway Passenger Station [J]. China Railway Science, 2009, 30(6):108-113. in Chinese) [16]陈彦, 史峰, 秦进,等. 旅客列车过站径路优化模型与算法[J]. 中国铁道科学, 2010, 31(2):101-107. (CHEN Yan,SHI Feng, QIN Jin, et al. Optimization Model and Algorithm for Routing Passenger Trains through a Railway Station [J]. China Railway Science, 2010, 31(2):101-107. in Chinese) [17]赵茜芮, 张琦. 基于同站台换乘的高铁车站作业计划优化编制[J]. 铁道科学与工程学报, 2016, 13(1):20-27. (ZHAO Xirui, ZHANG Qi. Optimization of High-Speed Railway Station Operation Plan Based on Across-Platform Transfer[J]. Journal of Railway Science and Engineering, 2016, 13(1):20-27. in Chinese) [18]铁道第三勘察设计院. 京沪高速铁路设计暂行规定[M]. 北京:中国铁道出版社, 2003.2.4 列车进路分配方案动态调整模型
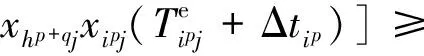
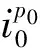

3 模型求解
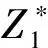
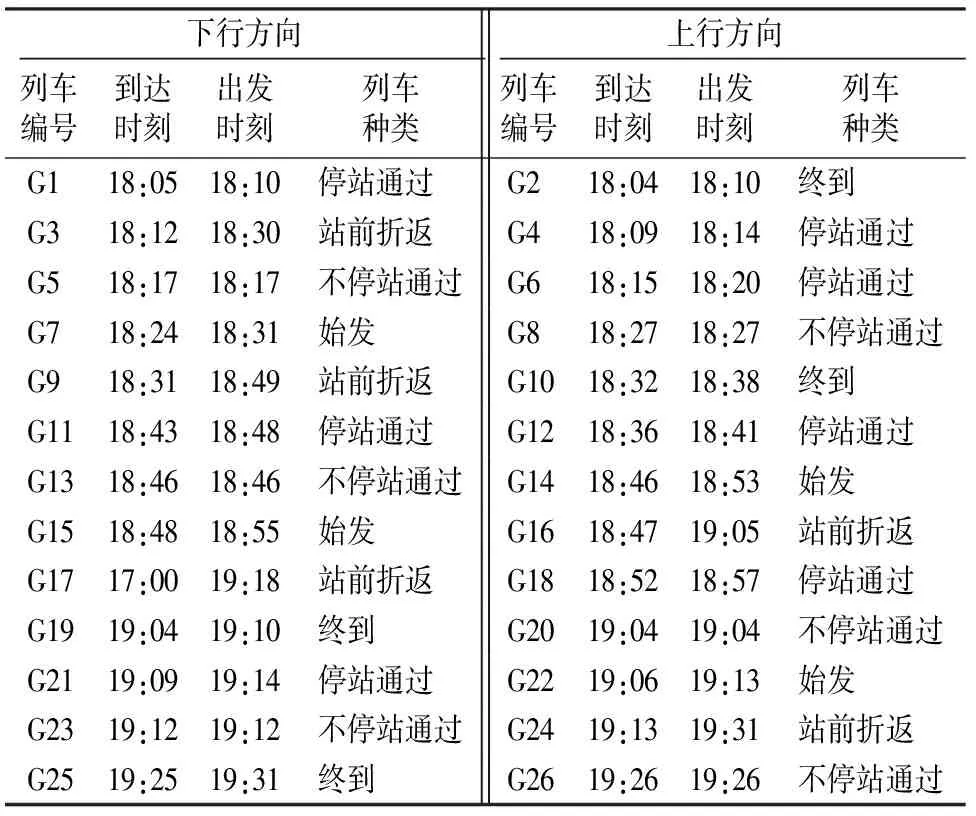
4 算 例




5 结 语

