基于概率模型的高速铁路地震预警实时性与准确性分析
王 澜,戴贤春,习年生,魏 猛
(中国铁道科学研究院 铁道科学技术研究发展中心,北京 100081)
高速铁路地震预警,是根据地震监测台站实时测定的地震P波初至信息快速估算的地震动参数,确定地震影响区域及其警报等级,在破坏性地震波到达之前,向地震影响范围内的铁路系统发布地震紧急处置信息,联动触发相关系统对运行列车采取减速或紧急制动。有效的高速铁路地震预警及紧急处置措施可使列车在地震灾害发生时的损失程度降至最小[1]。随着我国大范围高速铁路的开通运营,地震危害的潜在风险越来越突显,对地震预警系统的实时性与准确性要求也越来越高[2-3]。
国外学者早将地震视为随机事件,将概率论与数理统计方法用于地震预警中。Iunio等[4]提出基于概率模型发布警报的决策规则:若实时预测分析的地震动加速度峰值大于给定警报阈值的概率超过某一临界概率值时则发布警报。Andrew和Richard[5]采用统计学方法预测地震震源位置。Vladimir[6]基于概率模型证明了地震预警有效性随震中距和震级的不同而相应变化。Richard等[7]采用地震P波初至到系统发出预警信息的时延描述地震预警实时性,并基于概率模型进行了地震预警实时性分析。Huseyin等[8]采用统计学方法对地震监测台站密度进行了优化,进一步提高了地震预警的准确性。Simona等[9]和Aldo等[10]基于统计学方法系统研究了地震事件识别、地震要素估计和地震预警方法,研发的基于概率模型的地震预警系统(PRESTo)得到成功应用。Nakamura等[11]基于统计学方法实时估计地震要素,研发的紧急地震检测报警系统(UrEDAS)提高了日本新干线抗震减灾能力。Iunio等[12]建立了基于概率模型的地震漏报与地震误报数学模型,并用此评价地震预警的准确性。由此可见,概率论与数理统计方法是研究地震预警实时性与准确性的基础。
本文结合我国高速铁路技术特点与实际需求,建立数学概率模型,研究高速铁路地震预警实时性与准确性的分布特征和参数,通过实时性与准确性综合分析,提出高速铁路地震预警发布决策方法。
1 地震预警实时性和准确性模型
地震预警的实时性是指地震预警信息发出时刻相对于震中地震发生时刻的实时程度。本文采用首台站地震P波初至到系统发出预警信息的时延(简称为地震预警时延)进行评价,该时延越小,实时性越好。
地震预警的准确性是指震源定位、震级估算和地震发生时刻推算的准确程度;本文采用震源定位偏差进行评价,该偏差越小,准确性越好。
1.1 地震预警实时性常规概率分布模型
地震预警时延包括:信号滤波时延、数据采集时延、数据打包时延、数据处理时延、预警决策分析时延、数据发送时延、信息排队与传输时延等。受地理构造、地质条件、环境等不确定性因素影响,在不同的预警方式、数据采集处理、警报发布决策、数据传输条件下,地震预警时延具有较强的不确定性、离散性和随机性。实测数据表明,高速铁路地震预警时延具有单边、连续性、非对称型随机变量分布特征和统计规律性。
针对上述特征,地震预警时延可采用随机变量进行描述。常规的概率分布模型包括正态分布、对数正态分布、伽马分布模型等。
正态分布的概率密度函数、数学期望和方差分别为
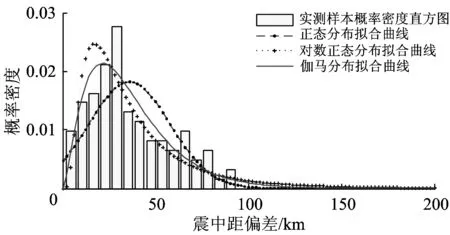
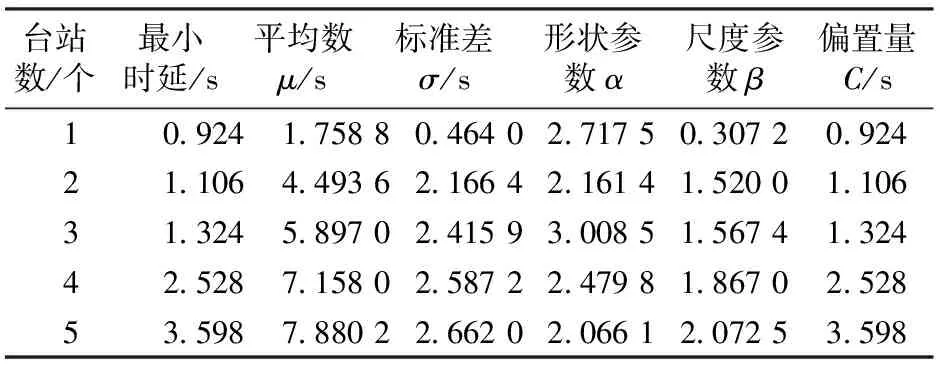
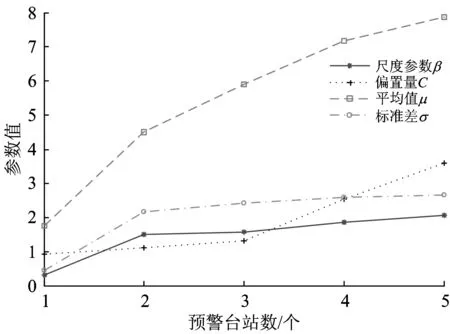
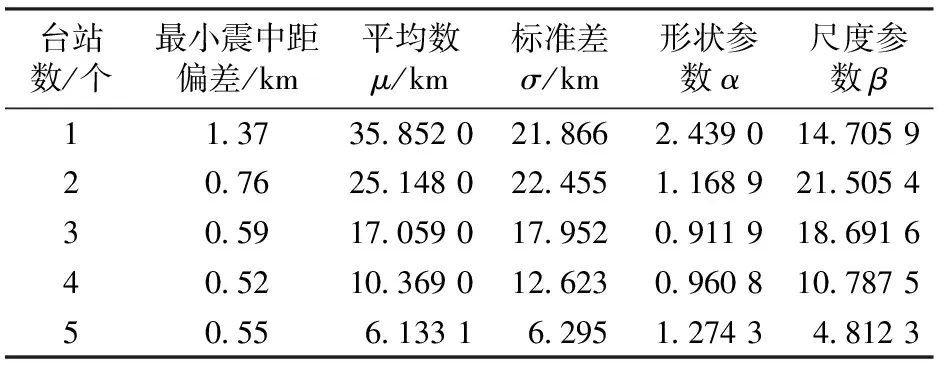
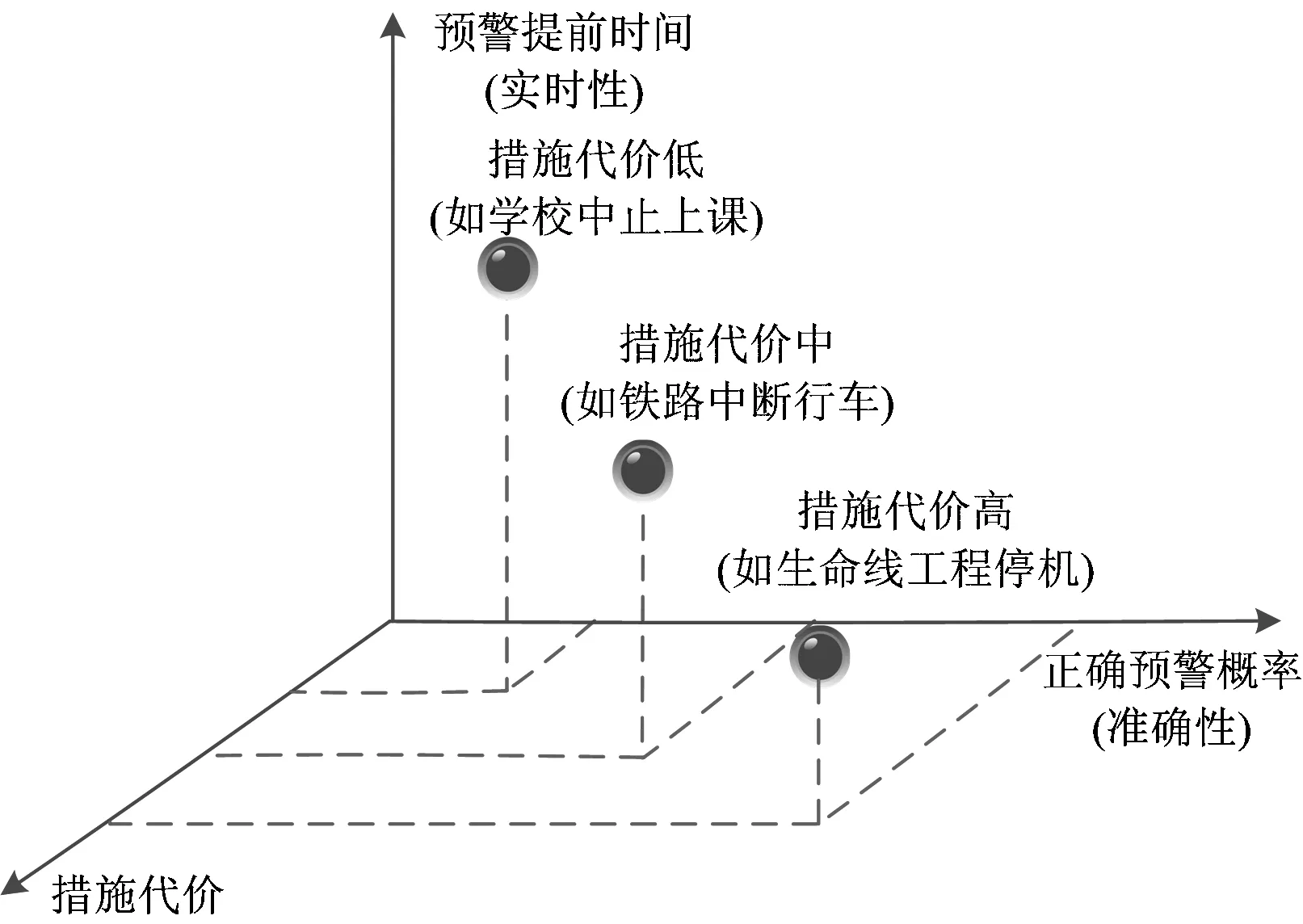
-∞ (1) E(X)=μ D(X)=σ2 式中:y为概率密度函数;X为随机变量;x为随机变量取值;μ为平均数;σ为标准差。 对数正态分布的概率密度函数、数学期望和方差分别为 0 (2) D(X)=(eσ2-1)e2μ+σ2 伽马分布的概率密度函数、数学期望和方差分别为 (3) E(X)=αβ D(X)=αβ2 式中:α为形状参数;β为尺度参数;Γ(α)为Gamma函数。 (4) 1.2.1偏置伽马分布模型的建立 实际上,信号滤波、数据采集、数据打包、数据处理、信息传输等时延均可视为由随机时延和固定时延两部分组成。随机时延由系统自然规律所决定,具有不确定性、离散性和随机性;而固定时延相当于接近常量的值,具有确定性和相对性。固定时延无法避免,也就是说,地震预警时延不会小于1个最小值,在这一最小值时间内生成预警信息的可能性不存在。因而,采用正态分布、对数正态分布或伽马分布等概率密度函数描述地震预警时延,均存在小概率情况下无法正确评价地震预警特征的问题。 鉴于此,为更精确地描述地震预警时延的特征,提出1种地震预警时延精确概率分布——偏置伽马分布。偏置伽马分布函数的特点是在常规的伽马分布函数基础上增加了1个偏置量,用于描述固定时延。偏置伽马分布的概率密度函数为 T=f(t|α,β) (5) 即T服从偏置伽马分布,记为 T~Γ0(α,β,C)t>C (6) 式中:T为时延随机变量;t为时延随机变量取值;C为偏置量,且C≥0,当样本数量足够大时,可以用样本最小值作为C的估计值;Γ0为偏置伽马函数,即 (7) 偏置伽马分布的数学期望和方差分别为 (8) (9) 特征函数为 Ψ(t-C)=[1-iβ(t-C)]-α (10) 1.2.2偏置伽马分布的性质 命题,设T~Γ0(α,β,C),则有 T-C~Γ(α,β) (11) 证明:将t-C=x代入式(3),由于x>0,则t>C,由此可得到式(5),从而可知T-C~Γ(α,β),即T-C服从伽马分布。 由此可知:偏置伽马分布是一种广义的伽马分布,当偏置量C=0时,偏置伽马分布即是伽马分布。因而,偏置伽马分布具有伽马分布的所有性质,是一种非对称、连续型分布。 1.2.3偏置伽马分布参数的极大似然估计 偏置伽马分布参数的极大似然估计方法如下:设ti是来自总体的样本,对于ti>C,将式(5)取似然函数可得 (12) 对式(12)两端取对数,得对数似然函数为 (13) 其一阶条件为 (14) (15) 由式(15)得到 [lnΓ0(α)]′ (16) 即 (17) 由此得出 (18) 即 (19) 综合式(15)和式(17)可得 (20) (21) 震源定位参数包括震中距、方位角、震源深度等。为简化起见,本文仅以震中距偏差和方位角偏差作为震源定位偏差,用于评价地震预警的准确性。根据震中距偏差的分布特征,设其服从伽马分布;方位角偏差取决于台站与震中的相对位置、预警台站数、计算方法等因素,当样本足够大时,宏观上可以认为其服从均匀分布。因此,以震中距偏差和方位角偏差作为二维随机变量,则震源定位偏差的服维概率密度函数为 (22) 其中,震中距偏差的概率密度函数为 (23) 式中:X为震中距偏差随机变量;x为震中距偏差随机变量取值;θ为方位角偏差随机变量。 采用新研发的某高速铁路地震预警系统进行地震预警性能试验。输入的地震波包括国内和日本天然地震记录数据共300条,其震中距分别为0~50,50~100和100 km以上;试验中将地震监测台站坐标按照各采集数据台站的实际经纬度进行动态设置,将天然地震记录数据按照各采集数据台站的实际时差进行回放;时延测试前利用GPS时间校准;地震监测台站数分别选取1,2,…,5个。 分别用正态分布、对数正态分布、伽马分布、偏置伽马分布函数对试验中测试的地震预警时延进行拟合对比,结果如图1和图2所示。由图1和图2可以看出:单台站与多台站地震预警时延均可以采用本文提出的偏置伽马分布概率密度函数进行拟合;偏置伽马分布概率密度函数可有效地描述地震预警时延的偏置量、非正态形状以及分布特征。经显著性检验,表明地震预警时延服从本文提出的偏置伽马分布,记为 图1 单台站地震预警时延概率密度函数拟合 TEEW=Γ0(α,β,C) (24) 图2 5个台站地震预警时延概率密度函数拟合 分别用正态分布、对数正态分布、伽马分布函数对试验中测试的地震预警震中距偏差进行拟合对比,结果如图3和图4所示。 图3 单台站地震预警震中距偏差概率密度函数拟合 图4 5个台站地震预警震中距偏差概率密度函数拟合 可以看出,采用伽马分布概率密度函数描述地震预警震中距偏差,与其他类型的分布函数相比,可以更有效地描述其单边性、连续性、非对称型的分布特征。经显著性检验,表明地震预警震中距偏差服从伽马分布,记为 XEEW~Γ(α,β) (25) 不同台站数量时,从首台站P波初至到地震预警监测铁路局中心系统发出地震预警信息,地震预警时延的偏置伽马分布概率密度对比如图5所示,时延统计值及偏置伽马分布概率密度函数参数的极大似然估计值见表1,时延统计值及偏置伽马分布概率密度函数参数变化规律如图6所示。 图5不同台站数量时地震预警时延的偏置伽马分布概率密度比较 表1 不同台站数量时地震预警时延统计值及偏置伽马分布参数估计值 图6不同台站数量时地震预警时延统计值及偏置伽马分布参数的变化规律 由图5、图6和表1不难看出:地震预警的实时性随着预警台站数的增加而下降;描述固定时延的偏置量C随着预警台站数的增加而明显增加,描述随机时延的平均数μ和标准差σ均成对数关系增长;偏置伽马分布概率密度函数的形状参数α与台站数无显著对应变化规律;尺度参数β与台站数对应关系密切,双台站比单台站的明显增加,此后随着预警台站数的增加而缓慢增加。 不同台站数量时地震预警震中距偏差偏置伽马分布概率密度对比如图7所示,震中距偏差统计值及偏置伽马分布概率密度函数参数的极大似然估计值见表2,震中距偏差偏置伽马分布概率密度函数参数变化规律如图8所示。 图7不同台站数量时地震预警震中距偏差的偏置伽马分布概率密度比较 表2不同台站数量时地震预警震中距偏差的统计值及偏置伽马分布参数估计值 台站数/个最小震中距偏差/km平均数μ/km标准差σ/km形状参数α尺度参数β1137358520218662439014705920762514802245511689215054305917059017952091191869164052103690126230960810787550556133162951274348123 图8不同台站数量时地震预警震中距偏差的统计值及偏置伽马分布参数变化规律 由图7、图8和表2不难看出:地震预警准确性随着台站数的增加明显提高;地震预警震中距偏差随着台站数的增加明显降低,平均值μ和标准差σ明显减小并快速收敛;偏置伽马分布概率密度函数形状参数α呈凹状曲线,尺度参数β呈凸状曲线。 依据表2给出的地震预警震中距偏差偏置伽马分布参数估计值,采用式(21)并经坐标变换后可得出震源定位偏差的二维概率密度函数,其中单台站与5个台站地震预警震源定位偏差的二维概率密度如图9和图10所示。 图9 单台站地震预警震源定位偏差二维概率密度 图10 5个台站地震预警震源定位偏差二维概率密度 由图9和图10可以看出:单台站地震预警震源定位偏差分布较为分散,并未向震源中心凝聚;随着预警台站数的增加,地震预警震源定位偏差快速减小,其偏差分布向震源中心凝聚,并由宽变窄,震源定位准确性明显提高。 由于地震事件、地质构造等的不确定性,地震预警的实时性与准确性是一对相互矛盾的性能参数。若过于强调实时性则必定会降低准确性,若提高准确性则一定会降低实时性。同时,准确性的下降又会减少系统的可信度[13]。 在实际工程应用中,地震预警的实时性和准确性的取舍还与采取地震紧急处置措施所付出的代价有关[13],三者的关系如图11所示。是否实时采取地震紧急处置措施,取决于紧急处置措施的影响程度和采取紧急处置措施所付出的代价。如果采取地震紧急处置措施的代价昂贵,则不必过于强调地震紧急处置的实时性,如生命线工程的停机可能代价昂贵,那就不得不最大限度地提高地震预警的准确性,以避免因可能发生的地震误报而采取紧急处置所带来的经济损失,但这样可获得的预警提前时间十分有限。对于学校而言,地震到来前,尽快让人员逃离到室外空旷场地躲避是最好的地震应对措施,该措施除造成一定的课时损失外几乎不必付出任何代价,因而获取充分的预警提前时间比过于强调预警准确性更为重要。 图11 地震预警的实时性和准确性与措施代价的关系 对于高速铁路而言,地震预警的实时性与准确性均很重要。实时性好,可在破坏性地震波到达之前采取有效的制动措施,避免运行的高速列车脱轨或倾覆;准确性好,可减少对正常运输秩序的影响。鉴于实际上实时性与准确性无法完全兼得,因此在进行地震紧急处置决策时需兼顾地震预警的实时性与准确性。为此,针对目前我国高速铁路地震预警台站布设现状,建议采用3个台站地震预警的方法。3个台站地震预警可实现:在70%概率情况下地震预警时延小于7 s;在70%概率情况下震中距偏差小于20 km。 (1)地震预警时延服从偏置伽马分布。随着预警台站数的增加,地震预警的时延增加,即地震预警的实时性相应下降,其中描述固定时延的偏置量C明显增加,描述随机时延的平均数μ和标准差σ成对数关系增长。 (2)地震预警震中距偏差服从伽马分布。随着预警台站数的增加,震中距偏差明显降低,即地震预警的准确性明显提高,其中平均数μ和标准差σ明显减小并快速收敛;随着预警台站数的增加,震源定位偏差快速减小,其偏差分布向震源中心凝聚,并由宽变窄,震源定位准确性明显提高。 (3)采用3个台站地震预警方法可兼顾实时性与准确性,是满足高速铁路地震预警需求的有效方法,实时性可达到全系统时延在70%概率情况下小于7 s,准确性可实现在70%概率情况下震中距偏差小于20 km。 [1]孙汉武,王澜,戴贤春,等. 高速铁路地震紧急自动处置系统的研究[J]. 中国铁道科学,2007,28(5):121-127. (SUN Hanwu, WANG Lan, DAI Xianchun, et al. Study on the Earthquake Urgent Automatic Alarm System of High-Speed Railway[J]. China Railway Science, 2007, 28(5):121-127. in Chinese) [2]宋晋东,李山有,马强.日本新干线地震监测与预警系统[J].世界地震工程,2012, 28(4):1-10. (SONG Jindong,LI Shanyou,MA Qiang. Overview on Earthquake Monitoring and Early Warning System for High-Speed Railway (Shinkansen) in Japan[J]. World Earthquake Engineering, 2012, 28(4): 1-10. in Chinese) [3]马强. 地震预警技术研究及应用[D]. 哈尔滨: 中国地震局工程力学研究所, 2008. (MA Qiang. Study and Application on Earthquake Early Warning[D]. Harbin:Institute of Engineering Mechanics, China Earthquake Administration, 2008. in Chinese) [4]IUNIO Iervolino, VINCENZO Convertito, MASSIMILIANO Giorgio, et al. Real-Time Risk Analysis for Hybrid Earthquake Early Warning Systems[J]. Journal of Earthquake Engineering, 2006, 10(6):867-885. [5]ANDREW B Lockman, RICHARD M Allen. Single-Station Earthquake Characterization for Early Warning[J]. Bulletin of the Seismological Society of America, 2005, 95(6): 2029-2039. [6]VLADIMIR Pinsky. Modeling Warning Times for the Israel’s Earthquake Early Warning System[J]. Journal of Seismology, 2015, 19(1):121-139. [7]RICHARD MAllen, HOLLY Brown, MARGARET Hellweg, et al. Real-Time Earthquake Detection and Hazard Assessment by ElarmS Across California[J]. Geophysical Research Letters, 2009, 36(5):1-6. [8]H SERDAR Kuyuk, RICHARD M Allen. Optimal Seismic Network Density for Earthquake Early Warning: a Case Study from California[J]. Seismological Research Letters,2013, 84(6): 946-954. [9]SIMONA Colombelli, ANTONIO Emolo, ALDO Zollo. A Duration Magnitude Scale for the Irpinia Seismic Network, Southern Italy[J]. Seismological Research Letters, 2014, 85(1):98-107. [10]ALDO Zollo, SIMONA Colombelli, LUCAElia, et al. An Integrated Regional and on-Site Earthquake Early Warning System for Southern Italy: Concepts, Methodologies and Performances[M]. New York: Early Warning for Geolo-gical Disasters, Advanced Technologies in Earth Sciences,Springer,2014: 117-137. [11]NAKAMURA Yutaka,SAITA Jun. UrEDAS, the Earthquake Warning System:Today and Tomorrow[M]. New York: Earthquake Early Warning Systems, Springer, 2007: 249-281. [12]IUNIO Iervolono, VINCENZO Convertito, MASSIMILIANO Giorgio, et al. The Crywolf Issue in Earthquake EarlyWarning Applications for the Campania Region[M]. New York: Earthquake Early Warning Systems, Springer, 2007: 211-232. [13]IUNIO Iervolino, GAETANO Manfredi, EDOARDO Cosenza. Earthquake Early Warning and Engineering Application Prospects[M].New York: Earthquake Early Warning Systems, Springer, 2007: 233-247.
1.2 地震预警实时性精确概率分布模型


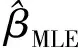


1.3 地震预警准确性概率分布模型
2 模型验证
2.1 实时性模型验证


2.2 准确性模型验证

3 地震预警实时性与准确性
3.1 实时性

3.2 准确性




3.3 综合分析
4 结 语

