高温超导发电机励磁系统变论域模糊控制
张兰勇,孟 坤,朱 帅
(1.哈尔滨工程大学 自动化学院, 哈尔滨 150001; 2.毫米波国家重点实验室, 南京 210096)
在863计划新材料领域项目的支持下,中船重工七一二研究所成功研制出我国第一台1 000 kW高温超导电动机,2012年4月实现满功率稳定运行。2012年7月,863计划“1 000 kW高温超导电动机”课题通过技术验收[1]。这标志着我国已经具备了兆瓦级高温超导电机设计、制造能力,成为国际上少数几个掌握高温超导电机关键技术的国家之一。但目前针对高温超导电机的研究较少,在电机的配套系统开发方面进展也十分缓慢,尤其是针对高温超导电机的励磁系统方面[2]。国外对高温超导电机的研究十分重视,美、德、日、韩等国采取一系列措施,完善体制,增加研究经费,制定研发计划,取得了重大突破。目前针对高温超导电机励磁系统的研究主要有以下几个难点:① 高温超导电机在设计和运行数据方面尚属于机密状态,对电机本体的工作状态研究开展困难;② 在励磁系统实际设计方面同样存在相应问题,由于高温超导电机的具体设计结构并未具体给出,对于励磁系统的硬件设计无法做到具有针对性。而对于励磁系统而言,控制策略决定了系统在稳定和故障状态下的工作性能,提高励磁系统的控制性能,对同步发电机和电力系统的安全稳定运行都有重要意义。励磁控制的作用十分重要,无论是系统工作在正常状态或是发生故障,励磁系统控制策略都不可或缺。励磁系统的性能对于高温超导电机的运行起着关键作用,对于几个关键技术指标如可靠性、稳定性以及电能质量等都有着重要影响。常规的PID控制策略结构简单,容易实现,并且具有一定的鲁棒性,能够满足一般精度要求。随着电力系统的发展,电力系统具有高度非线性、时变性,被控对象用常规PID励磁已经无法满足现代电力系统的要求,因此寻找更有效的控制方法。
1 高温超导电机励磁系统建模
高温超导电机励磁系统构成如图1所示。其中励磁系统部分由电力系统稳定器、旋转整流器和控制部分组成,控制策略将在后面的章节中进行具体设计分析。在励磁系统之外,输入为外部加入的给定,然后输出至高温超导电机转子绕组中。下面对各个部分的模型进行建模。
图2为高温超导电机励磁系统原理图,现根据此原理图对旋转整流器和电力系统稳定器部分进行建模设计。
1.1 旋转整流器数学模型
整流器的工作原理是根据二极管的特性即单向导电特性来决定的。交流输入、直流输出的工作方式是确保在同一时间内共阴与共阳这两组二极管之中只有一个二极管是导通的,共阴二极管中阳极电势最高的导通,而共阳二极管中阴极电势最低的导通,剩余的二极管都受非正向的电压因而不导通[3]。在电路中有负载时,通过不断变换导通的顺序,实现了整流,换流发生了6次,有6个换流点,整流桥输出的直流电压为线电压的包络线,一个周期中有6个均匀的波头,每60°间隔的负载电流的平均值是相同的,相应的负载电压平均值也是相等的,即
(1)
(2)
其中:u2为高温超导电机输出电压;ud为负载电压平均值。
当负载是一个大的电感与电阻时,电感可以不会出现波动平稳的输出电流,电路瞬时负载的电压波形与当电路负载中只含有电阻时是一样的,电路负载的电流为常数
(3)
其中时间常数T与整流电路的相数有关[4]。
1.2 电力系统稳定器(PSS)数学模型
在电力系统中,低频振荡一直是一个难以解决的问题,为了克服这个问题,科学家们研制了电力系统稳定器,作为一种附加励磁控制技术来抑制低频振荡[5]。它抑制低频振荡的方法为在励磁调节器中,引入附加信号,这个信号要领先于转速。通过这个信号,可以产生相应的正阻尼转矩,这个转矩可以用来调和励磁调节器在调解中负反馈所产生的负阻尼转矩。在PSS工作过程中,除了转速信号,它还需要对其他与振荡相关的信号进行采样,例如有功功率和频率,对采集的信号进行处理后同样融入之前所产生的信号中,可以对负阻尼信号进行更为有效的中和。
而输入信号方面,虽然可以对以上所提及的信号进行全面采样,但这样做的复杂性较高,不利于工业生产,故不同国家对于输入信号的选择不同[6]。有些国家,例如日本,采用ΔP作为输入量,而采用Δω即转速作为输入量的国家更多一些,例如美国。本文为了增加PSS的调节精度,决定同时选择ΔP和Δω作为输入量,电力系统调节器的数学模型如图3所示。
高温超导电机模型较为复杂,在此不详细给出,在仿真时将会采用相应的数学模型进行仿真。
2 励磁系统模糊PID控制策略设计与仿真
2.1 励磁系统模糊PID控制策略设计
PID控制策略的工作原理十分简单,也有其固有的缺陷。首先,PID算法的控制对象主要针对线性系统,对系统精确化建模要求较高,对于复杂系统往往控制效果较差;其次,由于放大器的饱和现象,会导致PID控制策略不得不对其微分信号进行削弱,同时由于被控对象的参数不断变化,而控制效果将会大打折扣;最后,传统PID算法对系统负载变化或是对干扰影响的自适应能力弱[7]。因此,传统的PID控制策略只适用于低负载、低非线性、扰动较小的情况,已经无法满足现代电力系统的要求,故本文提出了模糊PID励磁控制策略。
高温超导电机励磁系统的模糊PID励磁控制策略是以发电机的机端电压与给定值的偏差和偏差变化作为反馈信号,通过模糊逻辑规则推理出相应的控制信号,作用于高温超导电机上,实现对高温超导电机的励磁控制作用[8]。
作为一种自适应PID控制算法,模糊PID的特点在于在常规PID的基础之上加入了模糊推理算法。模糊控制不依赖精确的数学建模,对控制对象的线性化程度要求较低,而且还能有效的抗干扰,具有良好的自适应性和鲁棒性[9]。模糊PID控制算法将常规PID控制算法与模糊控制算法的优良性能相结合,是一种高效的智能PID控制算法[10]。
模糊推理系统(fuzzy system)的原理流程如图4所示。
本文设计的励磁控制系统,输入的量是端电压与期望值的偏差e,以及误差变化率e′。这两个量是具有物理意义的量,它们都有自身的变化范围,这个变化范围被称为系统的基本论域。被控对象所要求输出变量u的参数的变化范围为精确值,变化范围被称为模糊控制策略输出变量的基本论域。模糊化的第一个步骤就是将这两个实际输入变量模糊化以及将输出变量模糊化[11]。
输入e、ec分别表示模糊控制策略输入的端电压误差和端电压误差变化率;输出Δkp、Δki、Δkd分别为经过模糊控制策略处理得到的3个PID参数变量,其中Δkp为PID比例因子的整定增量,Δki为PID积分因子的整定增量,Δkd为PID微分因子的整定增量;u为模糊PID控制策略输出的控制量。
保留PID算法的设计则,只需要对模糊控制策略模块进行建模设计。该模糊控制策略为两输入单输出模型,设计步骤按照模糊控制策略原理如下:
1) 模糊量化
输入e、ec和输出Δkp、Δki、Δkd的模糊子集设为:NB,NM,NS,ZO,PS,PM,PB
分别表示:“负大”,“负中”,“负小”,“零”,“正小”,“正中”,“正大”。
确定e的论域为[-0.3,0.3],隶属度函数选择高斯型;ec的论域为[-0.1,0.1],隶属度函数选择高斯型;Δkp的论域为[-1,1],隶属度函数选择三角型,Δki的论域为[-0.1,0.1],隶属度函数选择三角型;Δkd的论域为[-0.05,0.05],隶属度函数选择三角型。模糊系统中的核心为知识库,而知识库的核心则为模糊规则,模糊规则是用来对输入与输出之间的模糊数学制定逻辑关系的。模糊规则的获取主要有两种方法:一种与PID 控制策略参数设定类似,为经验法,另一种为测试法。本文的模糊规则是利用 PID 算法参数调整的工程设计经验,并结合专家知识和实践中的控制经验加以总结而制定的,其制定原则是保证系统具有最佳的动静态性能。
2) 模糊PID控制量
输出模糊量反模糊化后得到整定好的 PID 修正参数,代入 PID 控制策略得到新的PID 3个环节参数为:
Kp=ΔKp+Kp0
Ki=ΔKi+Ki0
Kd=ΔKd+Kd0
(4)
式中,Kp0、Ki0、Kd0为初始PID参数值。模糊PID控制量规则见表1。

表1 模糊PID控制量规则
利用PID控制算法公式,得到模糊PID控制量如式(5)所示
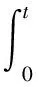
(Δkd+Kd0)ec(t)
(5)
2.2 励磁系统模糊PID控制策略下仿真
上文所设计的模糊控制策略,模糊PID中Kp、Ki、Kd3个值并不是固定值,所以在构建仿真子系统时无法像普通PID一样将3个值作为固定值,而是需要将这3个值作为输入值进行处理。同时,模糊控制策略中不仅需要端电压误差e这一个输入量,同时也需要端电压误差变化率ec作为另一个输入量[12]。模糊PID控制策略仿真模型如图5所示。图5中,Ke和Kec分别为模糊控制策略中的输入值。
仿真时间定为10 s,算法设置为ode23tb。PID控制策略控制下,设置几个控制参数分别为:Kp=20,Ki=4.2,Kd=0.21,随后设置模糊控制策略,将量化因子设置为Ke=3、Kec=1;比例因子设置为Kup=26、Kui=1、Kud=10。常规工作状态仿真结果如图6所示。
之前本文所设计的仿真模型都是针对高温超导电机在正常工作状态下的,而在正常工作状态下会发生很多无法预知的突发状况,这些也是励磁系统需要面对的问题。在正常工作状态下,电机有时需要面对输出端短暂短路的情况,在本研究中,通过模拟端电压出线端短路来测试励磁系统在面对故障时的调节效果。短路的模拟方式如图5所示,通过在无穷大电网上添加三相短路故障模块来模拟短路故障。故障时间设为从15 s到15.1 s,仿真时间设为20 s,其他参数设置与常规工作状态下参数相同。故障状态下端电压和励磁电压的仿真曲线如图7、图8所示。
3 励磁系统变论域模糊PID控制策略设计与仿真
3.1 励磁系统变论域模糊PID控制策略设计
模糊控制策略所推出的算法中,难免具有一定的非线性成分,这是由于模糊规则的复杂,会降低控制效果;控制精度取决于控制规则数量、隶属度函数选择及专家经验,系统调试复杂。模糊控制具有较强的鲁棒性,自适应能力差,而变论域模糊控制则有效地对其进行了改进。
对于变论域的模糊控制策略的设计不需要太多的领域专家知识,只要知道规则的大致趋势;相比模糊控制策略对控制规则、隶属度函数和等距划分没有特别高的要求,系统设计更为简单,精度也更高[13]。所以,变论域模糊控制是一种高精度的模糊自适应算法,能够有效地应对控制对象的非线性、难以建模和模型参数变化的难点。图9为常见的变论域模糊控制原理框图。
变论域即是输入输出论域随着两个输入变量参数的变化而变化,将输入输出论域变化表示为如式(6):
X1(x)=[-α(x)E,α(x)E]
X2(x)=[-β(x)Ec,β(x)Ec]
Y(x)=[-γ(x)U,γ(x)U]
(6)
式中:X1(x)、X2(x)、Y(x)为变论域;α(x)、β(x)、γ(x)分别为输入变量e、ec、输出变量u的论域伸缩因子,大小与输入变量e、ec有关,表示为函数形式。这就是所谓的变论域,即实现了论域随误差的变化而变化。以输出论域为例,其论域伸缩情况如图10、图11所示。由图可知,变论域的核心也就是伸缩因子的选取,伸缩因子的大小变化决定了论域变化后的形状,更是直接影响变论域模糊的控制性能[14]。
对于伸缩因子的选取,基于数学模型的伸缩因子方法是通过伸缩因子的定义和性质,将伸缩因子表示成输出变量的函数,常用的输入输出论域伸缩因子的函数模型如式(7):
(7)

本系统的模糊控制通过计算机处理器来实现,为了便于在其他控制策略上移植,选择采用离散时间系统进行控制策略设计。给定初始控制规则R(0)=R,初始论域X1=[-E,E],X2=[-EC,EC],Y=[-U,U]上的线性基元组分别为{Ai}(1≤i≤p), {Bj}(1≤j≤q), {Cij}(1≤i≤p, 1≤j≤q),峰值点满足
-EC=x21 -E=x11 令x1i(0)=x1i,x2j(0)=x2j,yij(0)=yij,-U∈=y11 步骤1:初值输入x1(0)∈X1,x2(0)∈X2,得到输出: y(1)=Fx10,x20= (8) 步骤2:y(1)施加对象后得到系统输出,反馈给系统参考输入相比较,得到控制策略的输入x1(1),x2(1)。令: x1i(1)=α(x(1))x1i(0) (9) x2j(1)=βx1(1),x2(1)x2j0 (10) yij(1)=F(x1i(1),x2j(1))= (11) y(2)=F(x1(1),x2(1))= (12) 步骤k:y(k)施加对象后得到系统输出,反馈给系统参考输入相比较,得到控制策略的输入x1(k),x2(k),同理,有: x1i(k)=α(x1(k))x1i(0) (13) x2j(k)=βx1(k),x2(k)x2j0 (14) yij(k)=F(x1i(k),x2j(k))= (15) yij(k+1)=F(x1(k),x2(k))= (16) 综合以上步骤,得到上述双输入单输出自适应模糊控制策略输出为: Asαx1(k)x1i(0)· Bjx2(k)/βx1(k),x2(k)· Btβx1(k),x2(k)x2j(1)yst(0) (17) 此外,当x1(k)→0,x2(k)→0时,y(k+1)→0。 常规工作状态下仿真结果如图12所示。 故障状态下端电压和励磁电压的仿真曲线如图13、图14所示。 从两种控制策略的常规工作状态仿真曲线图6与图12中可以明显看出在模糊PID控制策略控制下的曲线没有超调,在经过短暂的抖动后进入稳态,没有静态误差。在变论域模糊控制策略下的励磁电压曲线相对普通模糊控制更加平滑,不仅没有超调,也没有进入稳态之前的抖动。 表2是两种控制策略在常规工作状态下控制策略性能对比。 控制类型性能指标上升时间/s超调量/%调节时间/s稳态误差/%模糊PID0.350.20.850.2变论域模糊PID0.500.10.800.0 根据表2的数据,可以得到分析结论。在调节时间和稳态误差以及超调量这几个方面,虽然模糊PID在上升时间上快于变论域模糊PID,但是从实际的响应曲线中可以看出,模糊PID在进入稳态误差之前的抖动较大,实际调节时间是要比变论域模糊PID长的。 由此可以确定,变论域模糊控制在常规工作状态下,控制效果上要优于模糊PID。 在故障状态下,通过对端电压的两个响应曲线图7与图13的对比可以看出,在模糊PID控制策略控制下的端电压响应曲线中电压的调节时间明显较长,变论域模糊PID控制调节时间较短,具体性能指标如表3所示。从表3的数据可知,在模糊PID控制下,端电压的调节时间从开始调节到故障消失端电压输出恢复正常花费了0.03 s。两组波形的对比证明变论域模糊PID的确是相对模糊PID在控制精度和效果上都占优势。 表3 短路状态下两种控制策略端电压性能指标 在励磁电压方面,从图6与图12中可看出,模糊PID在进入稳态之前有一个小小的抖动,振荡两次进入稳态,但变论域模糊PID则没有这方面的问题,同时从图8与图14中可以看出,在励磁电压响应方面变论域模糊PID的精确度更高,进入稳态比较平滑。具体性能指标如表4所示。 表4 短路状态下两种控制策略励磁电压性能指标 通过表4的数据可以分析出,在短路状态下,变论域模糊PID的调节时间比模糊PID的调节时间快0.03s,并且变论域模糊PID没有稳态误差,所以无论是在调节时间还是稳态误差上,变论域模糊PID控制都在控制性能上有着绝对的优势。 本文利用模糊控制理论,根据励磁系统的控制要求和特点,结合传统PID和变论域控制的优点,构建了一种变论域模糊PID控制策略。因为模糊控制不需要有精确的系统数学模型,所以基于模糊理论构建的励磁调节器具有更广泛的调节范围。仿真实验结果表明:变论域模糊PID控制在调功、调压和大扰动时具有更好的控制精度、反应速度和抗干扰能力,能够有效改善系统各状态量及输出量的动、静态性能,提高系统的稳定运行能力。 参考文献: [1]赵朝会,李进才.超导发电机的研究现状及发展前景[J].上海电机学院学报,2013(6):314-321. [2]贺徽,周建中,谭建华,等.基于Mamdani模糊PID的同步发电机励磁控制[J].华中科技大学学报(自然科学版),2010(2):34-37. [3]ESTEBAN A,DEVAIAH N,PANAGIOTIS L,et al.Methodology to assess the performance of an aircraft concept with distributed propulsion and boundary layer ingestion using a parametric approach[J].Proceedings of the Institution of Mechanical Engineers Part G-Journal of Aerospace Engineering,2015,229(4):682-693. [4]WOLFGANG N,JOERN G,JOACHIM F.Test results from siemens low-speed,high-torque HTS machine and description of further steps towards commercialisation of HTS machines[J].Physica C:Superconductivity and Its Applications,2012,482:105-110. [5]刘胜,张玉廷,余辰光.船舶电力推进系统电机组三维模糊控制[J].中国电机工程学报,2012,32(3):117-123. [6]刘子全,高磊,赵娴,等.一种可有效提高临界增益的改进型电力系统稳定器[J].中国电机工程学报,2015,35(8):1875-1881. [7]IOAN F,IOSIF S.Adaptive fuzzy PI controller with shifted control singletons[J].Expert System with Applications,2016,54:1-12. [8]韩兵,周腊吾,陈浩,等.基于变论域模糊控制的大型风电机组偏航系统[J].电工电能新技术,2016,35(8):15-20. [9]MIER L.A,BENITEZ J.S,LOPEZ R,et al.Adaptive fuzzy control system for a squirrel cage induction motor[J].IEEE Latin America Transactions,2017,15(5):795-805. [10] A-RONG K,KWANG-MIN K,HEECHEOL P,et al.Performance analysis of a 10 kW superconducting synchronous generator[J].IEEE Transactions on Applied Superconductivity,2015,25(3):1-4. [11] CHEN QING,NAN YU-RONG,ZHENG HENG-HUO,et al.Full-order sliding mode control of uncertain chaos in apermanent magnet synchronous motor based on a fuzzy extended state observer[J].Chinese Physics B,2015,24(11):161-166. [12] KARMAKER H,SARANDRIA D,HO M T,et al.High-Power dense electric propulsion motor[J].IEEE Transactions on Industry Applications,2015,51(2):1341-1347. [13] 崔家瑞,李擎,张波,等.永磁同步电机变论域自适应模 糊PID控制[J].中国电机工程学报,2013,33(S1):190-194. [14] 李红伟.变论域模糊控制的无刷直流电机控制系统[J].控制工程,2010,17(5):599-602.3.2 励磁系统变论域模糊PID控制策略下仿真
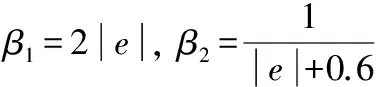
4 高温超导电机励磁系统仿真分析



5 结论

