基于广义对数线性模型的可靠性评估方法
王 华,张静远,王 鹏,冯 杭
(1.海军工程大学 兵器工程系, 武汉 430033; 2.海军工程大学 理学院, 武汉 430033)
为了评估高可靠、长寿命产品的可靠性,研究人员通过采用加速寿命试验技术快速获得产品的失效数据,再通过加速模型将试验中获得的失效数据进行外推,得到产品在正常应力下的可靠性。因此,利用加速试验评估产品可靠性的关键便是加速模型。
许多产品在使用过程中会同时受到温度和振动应力的作用(如雷弹在装载期间、航天电连接器在使用期间),如何构建有效的加速模型对上述产品的可靠性进行评估,是研究人员关注的重点。目前,国内外研究人员在同时考虑温度应力与振动应力的加速模型方面已展开了相关研究。Donald B.Barker[1]通过研究印刷电路板焊点的寿命,提出了一种描述温度和振动应力的复合加速模型;陈文华[2]将广义艾林模型应用于航天电连接器的加速寿命研究中,提出了一种同时考虑温度应力与振动应力的加速模型;M.B.Srinivas等[3]基于断裂力学疲劳定律提出了一种描述温度、机械振动应力和电应力的复合加速模型等。上述加速模型都是基于特定产品失效的物理化学机理提出的,该类加速模型通常称为物理加速模型。上述加速模型的预测结果虽然较为可信,但是仅适用于产品的失效机理与加速模型相一致的场合,其是否适用于其他类型产品有待商榷,即存在外推风险。另外,这些模型在构建时忽略了应力之间的相互影响,其预测结果是否准确也有待研究。针对上述物理加速模型预测结果较为可信但存在外推风险的特点,在考虑应力之间相互影响的情况下,本文提出一种基于广义对数线性模型的复合加速模型,以求解决单一的物理加速模型在评估产品可靠性时存在的问题。
1 常用的加速模型
当前,在加速试验研究中,常用加速模型有阿伦尼斯模型、逆幂律模型、艾林模型和广义对数线性模型等。
1) 阿伦尼斯(Arrhenius)模型
在加速试验中,常常把温度应力作为加速应力,因为温度升高会加快产品(如电子器件、绝缘材料等)内部的化学反映,加快产品失效速度。阿伦尼斯在1880年研究了这类化学过程,在研究大量数据的基础土提出如下加速模型,即阿伦尼斯加速模型[4]:
ξ=AeE/KT
(1)
式(1)中:ξ是产品的某寿命指标,如平均寿命、中位寿命等;A是一个与产品和试验有关的常数,且A>0;E为激活能,与退化机理有关,以ev 表示;K= 8.617×10-5ev/℃是波尔兹曼常数;T为绝对温度。
2) 逆幂律模型
在加速试验中,机械应力和电应力也经常作为加速应力。产品的某些寿命特征与机械应力、电应力有如下的关系[4]:
ξ=AVα
(2)
其中:ξ为某寿命特征量;V表示采用的加速应力水平;A、α是与失效模式和实验方法有关的常数。
3) 艾林(Eyring)模型
单应力艾林模型是由量子力学原理推导得出的用以表示产品的寿命特征与绝对温度之间的关系[4]:
(3)
式(3)中:T是绝对温度;K是波尔兹曼常数;A、B是与失效模式和试验有关的常数。
4) 广义对数线性模型
Nelson通过对试验数据的拟合,从数学的角度提出了广义对数线性模型。该模型将产品的某寿命特征量看做是z个应力元素组成的矢量S=(s1,s2,…,sz)的函数。描述加速应力与特征寿命之间函数关系的加速模型如下:
lnξ=γ0+γ1φ1(s)+…+γzφz(s)
(4)
式(4)中:γ0,…,γz为模型参数;φ1(s),…,φz(s)为应力元素矢量S中一个或多个应力元素的函数。利用广义对数线性模型进行加速试验研究的时候,将φx(s)(x=1,…,z)用相应的加速应力函数项替换,就得到了一种多应力加速模型。
在上面介绍的4个加速模型中:阿伦尼斯模型、逆幂律模型和艾林模型与产品失效的物理化学机理相关,这三种加速模型通常称为物理加速模型。广义对数线性模型是基于物理加速模型在统计分析的基础上构造的数学假设[5],因此称为数学加速模型。数学加速模型的预测结果不如物理加速模型可信,但适用范围较为广泛。
2 建立基于广义对数线性模型的复合加速模型
对阿伦尼斯模型表达式(1)两边取对数,有
lnξ=γ0+γ1φ(T)
(5)
其中,γ0=lnA,γ1=E/K,φ(T)=1/T。
对逆幂律模型表达式(2)两边取对数,有
lnξ=γ0+γ1φ(V)
(6)
其中:γ0=lnA,γ1=α,φ(V)=lnV。
对艾林模型表达式(3)两边取对数,有
lnξ=γ0+γ1φ(T)-lnT
(7)
其中:γ0=lnA,γ1=B/K,φ(T)=1/T。
从上述加速模型的数学表达式可以看出,这3种物理加速模型都可以看做是广义对数线性模型的特殊情况,通过广义对数线性模型可将不同应力同时作用下的加速试验信息进行融合,实现不同应力下特征寿命的相互转化[5-6]。
因此,产品在温度和振动应力作用下的寿命特征值与加速应力之间的函数关系可表示为
lnη=γ0+γ1φ1(T)+γ2φ2(V)+γ3φ3(T,V)
(8)
式(8)中:η为产品寿命特征值(如平均寿命、可靠寿命等);γ0,γ1,γ2,γ3为模型待估计参数;φ1(T)=1 000/T为温度应力的函数,T为绝对温度;φ2(V)=lnV为振动应力的函数,V为振动应力;φ3(T,V)=φ1(T)φ2(V)为考虑应力之间存在相互影响的情况下,温度应力与振动应力交互作用的函数。
3 可靠性加速试验评估
1) 基本假设。在进行加速试验时,做如下假设:产品的寿命服从指数分布;在所施加的不同应力水平下,产品的失效机理保持不变;随机抽取的产品在预定的加速应力水平下进行试验,失效时间统计独立。

3) 参数估计。试验中,在应力水平Si下,测试区间tij-1,tij(j=1,…,mi)内,试验产品失效的概率为
pij=p(tij-1 e-λitij-1-e-λitij (9) 在时间区间0,τi内试验产品未失效的概率为 (10) 因此,当n个产品在k应力水平下进行恒定应力加速寿命试验时,产品可靠性加速模型的参数γ0,γ1,γ2,γ3的似然函数为 (11) 对似然函数等式两边取对数,可得: (12) 得到对数似然函数后,将λi与温度应力和振动应力的之间的函数关系代入上式,模型中的参数γ0、γ1、γ2、γ3的极大似然估计可由以下公式求得: (13) (14) (15) (16) 对上述式子采用直接极大化方法求解模型参数时,因为似然函数的形式过于复杂,所以通常无法得到参数的解析解。而结合牛顿-拉夫迭代算法等数值解法求解似然函数的方法也可能会遇到不收敛、局部极值以及对初始值敏感等问题。针对参数求解中的这些问题,本文选用遗传算法[7]对模型参数进行极大似然估计。 遗传算法是一种在模仿生物遗传进化原理的基础上,引入随机理论形成的一种全局优化算法。在求解参数的过程中,通常结合专家经验和工程实际,先赋予参数一定的取值范围,使算法在一定的区间范围内进行搜索,以便算法能快速的搜索出解空间中的全体合理解。通过对实例中求解得到的参数进行分析,证明了遗传算法具有较好的参数求解效果。 4) 可靠性评估 结合加速模型和文献[8]可知,当产品的寿命服从指数分布时,产品的平均寿命η、特征寿命te-1、失效率λ和可靠寿命tR为 (17) (18) (19) (20) 如果加速模型参数已知,就可以求得正常工作应力水平Su=Tu,Vu下产品的平均寿命、特征寿命、可靠寿命等可靠性指标,实现对产品可靠性进行评估的目的。 本文以航天电连接器在温度应力与振动应力综合作用下的加速寿命试验[9]为例,通过对试验数据的统计分析讨论所建立的复合加速模型的适用性。 试验共投入4组23个样品,并分别在不同的应力水平下进行加速试验。定时对受试样品进行测试,直到所有样品全部失效时试验结束。样品的试验结果[10]如表1所示。 根据前期对产品可靠性的研究,可以粗略的确定各参数的取值范围为 -10≤γ0≤5,-5≤γ1≤5 -10≤γ2≤5,-5≤γ3≤5 然后利用遗传算法解得参数γ0,γ1,γ2,γ3的估计值为 γ0=-3.028 6,γ1=0.987 2 γ2=-0.975 8,γ3=-0.325 1 表1 不同应力条件下产品各测试区间的失效数 表2 各应力下产品平均寿命的预测值与实测值的相对误差 本文通过广义对数线性模型对阿伦尼斯模型和逆幂律模型进行有机融合,建立了一种评估产品可靠性的双应力加速模型,得到了产品可靠性特征值与应力之间的函数关系;通过对试验数据的统计分析,利用遗传算法求解得到了模型参数的估计值;通过对产品试验寿命和模型估计寿命的比较分析,表明了该模型具有较好的预测精度,证明了该模型的适用性。 参考文献: [1]BARKER D B,DASGUPTA A,PECHT M G.PWB solder joint life calculations under thermal and vibrational loading[C]//Reliability and Maintainability Symposium,1991.Proceedings.IEEE,2002:451-459. [2]陈文华.航天电连接器环境综合应力加速寿命试验与统计分析[J].浙江大学学报,2006(2):348-351. [3]SRINIVAS M B,RAMU T S.Multifactor aging of HV generator stator insulation including mechanical vibrations[J].Electrical Insulation IEEE Transactions on,1992,27(5):1009-1021. [4]茆诗松,王玲玲.加速寿命试验[M].北京:科学出版社,1997. [5]李晓阳,姜同敏.加速寿命试验中多应力加速模型综述[J].系统工程与电子技术,2007,29(5):828-831. [6]陈循.加速寿命试验技术与应用[M].北京:国防工业出版社,2013. [7]段玉倩,贺家李.遗传算法及其改进[J].电力系统及其自动化学报,1998(dl):39-52. [8]张志华.可靠性理论及工程应用[M].北京:科学出版社,2012. [9]钱萍.航天电连接器综合应力加速寿命试验与统计分析的研究[D].杭州:浙江大学,2009.4 实例分析
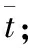



5 结论

