联合结构张量与运动学反偏移的立体层析数据空间提取与反演策略研究Ⅱ:实践
熊 凯,杨 锴,邢逢源,叶云飞,薛 冬
(1.同济大学反射地震学科组,上海200092;2.中海石油研究中心,北京100027)
层析是地震反演中关键的一环[1],立体层析是一种特色层析反演方法,它将一个局部相干同相轴在炮道集与检波点道集内的射线参数水平分量(Psx和Prx,以下简称地表观测P参数)纳入到数据空间之中,使得数据空间的信息相比传统反射层析更为丰富。除旅行时t外,地表观测P参数与炮检点坐标也都纳入到立体层析数据空间中,使得立体层析成为层析成像方法中唯一一种可以同时反演速度、反射点位置、反射张角与构造倾角的方法[2]。传统立体层析一般选择在数据域利用倾斜叠加能量谱拾取数据空间[3-5],该方法对二维数据尚可一用,但是对三维数据则基本失去可操作性。近年来王宇翔等[6]、YANG等[7]基于结构张量实现了在二维、三维叠前数据域提取射线参数水平分量的快速算法,使得基于结构张量的二维、三维高密度立体层析反演成为现实。使用结构张量直接在叠前数据域搜索的优点是能够快速得到高密度的数据空间,同时无需人工干预。但是基于结构张量的快速自动拾取面临绕射波、多次波及侧面反射波难以自动识别的问题。文献[2]认为单次反射与单次绕射都可以用于立体层析反演,但是杨锴等[8]通过数值实验证实了一次绕射波不适用于立体层析,必须将其排除在立体层析数据空间之外。
本系列文章第一篇[8]已经明确:立体层析的反演成功与否建立在数据空间是否来自可靠的并有助于目标段反演的一次反射波的基础上,即需提取可靠的特征波场[9]。同时,作者基于CHAURIS等[10]提出的P参数校正公式实现了运动学反偏移,即在叠前成像道集上提取构造倾角与剩余曲率(RMO)信息,然后利用P参数校正公式获得正确的地表观测射线参数水平分量[11]。该方法的优势在于:处理人员可结合自己的地质认识从共偏移距成像道集上识别出可靠的、对应于关键(可靠并有助于目标段速度反演)反射层一次反射波的成像位置,并在这些位置提取构造倾角与RMO信息。这样在实施运动学反偏移后得到的叠前数据域内数据点信息对应于关键反射层的一次反射波,这些信息才是立体层析反演所需的最佳数据空间,避开了不利于立体层析的绕射波、多次波和侧面波。
杨锴等[8]基于上述思路提出一种在数据域应用结构张量而后在成像域实施运动学反偏移以获得更佳立体层析数据空间的两步法实施策略,并利用理论数据验证了其可行性。当该策略用于实际数据时,还需考虑如何在深度域有效提取反射信息等细节问题。本文首次将该策略应用于中国南海某深水二维地震数据的偏移速度建模处理,并设计出一套实用的技术流程。南海某二维实际数据的偏移速度建模实践表明,上述两步法策略有效提高了实际数据的反演精度,是一种获得更佳立体层析数据空间的有效途径。
1 三维结构张量方法原理及其在二维成像数据体上的应用
为保证叠前偏移成像体中运动学信息的搜索精度,本文将二维叠前数据体视为一个在共中心点X方向、深度Z方向和共偏移距H方向构成的(X,Z,H)域三维数据体,使用三维结构张量同时获得运动学反偏移所需的构造倾角和RMO信息。为此首先简单介绍三维结构张量算法的工作原理,更多细节请参考文献[12]。
对三维图像中某一样点而言,其梯度平方张量矩阵定义如下:
(1)
式中:gx,gy,gz,分别表示该样点处的两个梯度水平分量与梯度垂直分量。梯度平方张量的含义是图像中某一样点处,对应于单一走向的梯度方向。为提高低信噪比图像中走向信息预测的稳定性,在该样点附近的邻域内,比如一个5×5×5样点区域内统计125个这样的梯度平方张量,并将它们加权叠加获得一个光滑的梯度平方张量矩阵G′,该矩阵将有助于获得该点处比较稳定的走向信息。将G′写作:
(2)
式中:〈·〉代表光滑后的梯度平方;k(x,y,z)代表光滑加权矩阵。获得光滑的梯度平方张量矩阵G′之后,针对该半正定矩阵G′,通过求解特征方程|G′-λI|=0得到其特征值与特征向量:
(3)
特征向量与特征值描述了图像局部线性结构的方向性与能量分布。特征向量v1(v11,v12,v13)代表切平面的单位法向量,同时代表了图像的主结构方向,其对应特征值λ1为最大特征值,对应于特征向量方向v1的能量;特征向量v2(v21,v22,v23)代表在切平面内且与最佳拟合线即切线相垂直的单位法向量,λ2为对应方向的特征值,对应于特征向量方向v2的能量;特征向量v3(v31,v32,v33)是与由v1,v2构成的平面正交的方向,同时也代表了图像的灰度变化最大的方向,λ3为对应方向的特征值,对应于特征向量方向v3的能量。三维时有两个方向的线性度概念(1-λ2/λ1)和(1-λ3/λ1),反映局部方向的一致性。对于
地震数据而言,线性度的含义等价于同相性。
运动学反偏移所需要的构造倾角ξ与RMO信息tanφ(如图1所示)可利用主特征向量v1方向的三个分量由下式计算得到:
(4)
图2a说明了为什么二维成像数据可以视为三维数据体来处理;图2b显示了对于本文使用的理论数据中某二维叠前成像体的一小段(这一小段共成像道集(CIG)显然可视为(X,Z,H)域内的三维数据体)。应用三维结构张量搜索到的数据点(用黑色表示)以及利用相关属性参数计算得到的特征向量v1,v2,v3。可以看出,由于三维梯度平方结构张量算法的稳定性,可以可靠地估算实际地震数据的局部倾角。

图1 在叠前深度偏移体(X,Z,H)上拾取局部同向轴[10]a 共偏移距成像道集(拾取构造倾角ξ); b 共成像点道集(拾取RMO信息tanφ)
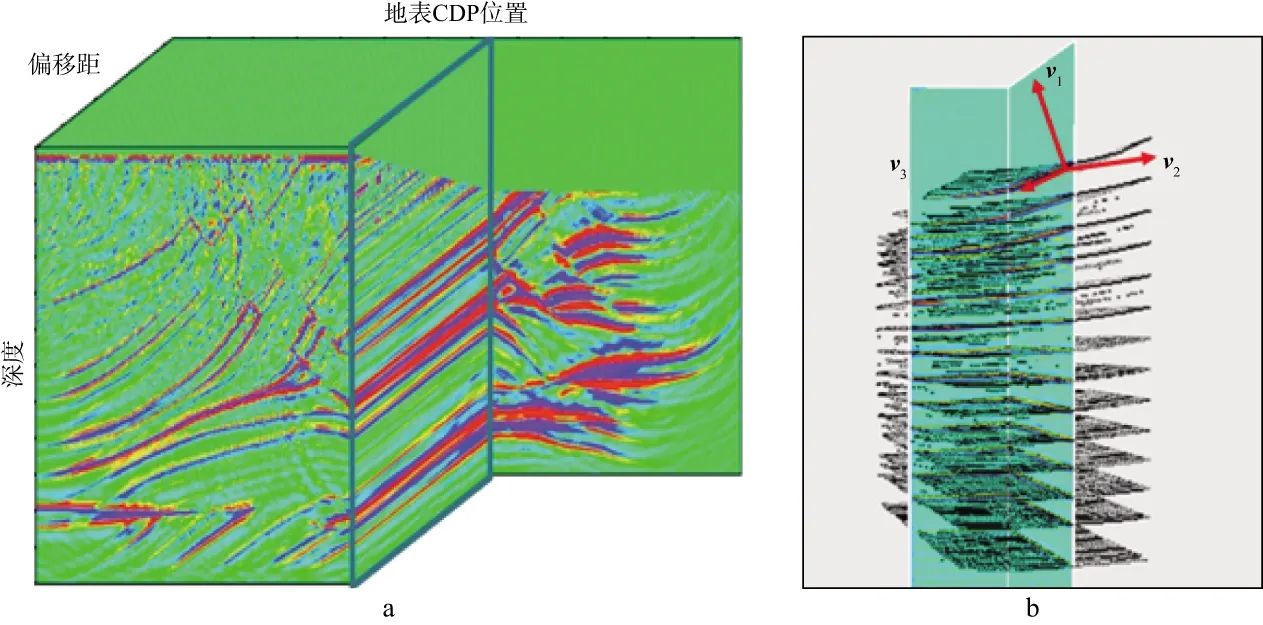
图2 三维结构张量搜索a 将二维叠前深度成像体视为三维数据体; b 三维结构张量示意图及搜索到的数据点(黑色表示)和计算得到的特征向量v1,v2,v3
2 流程设计
从上节可知,在叠前数据域应用结构张量[5]获得初始数据空间,即可获得初始反演速度与初始成像数据体。上述过程可以全自动实现,无需人工干预,然后将初始成像数据体视为一个三维数据体,应用三维结构张量算法同时获得反偏移所需的高密度分布的构造倾角和RMO信息。这样实现的好处是可以更好地保证构造倾角和RMO信息的提取精度,同时计算成本并没有明显增加。但对于实际数据而言,我们认为最好选择叠前深度偏移后的小、中、大至少3个共偏移距道集,在这3个成像道集内人工拾取对应于关键(可靠并有助于目标段速度反演)反射层的可靠数据点,再利用之前获得的高密度RMO信息将这些数据点延拓到其它未拾取的偏移距道集,这样即可提取出可靠的成像域数据点信息。最后,利用运动学反偏移将上述挑选后的成像域数据点反偏移到数据空间,获得更为可靠的立体层析数据空间。
基于上述考虑,本节提出了适用于二维实际数据的实用化流程。设计思路如下:在人工拾取之前,对初始叠前深度偏移获得的叠前成像体应用三维结构张量算法先进行一次初始拾取,适当放低初始拾取的线性度门槛值,使叠前成像体内的连续同相面能够尽可能多地被拾取,这样就获得了高密度分布的构造倾角ξ与剩余曲率信息tanφ。注意这个初始高密度拾取在获得一次反射波的运动学信息(旅行时、炮点坐标、检波点坐标、炮点P参数、检波点P参数)的同时,必然也获得了其它具有同相性特征的波现象的运动学信息,这些波现象所对应的运动学信息并不是立体层析所需要的,应该将其排除在外。因此,在获得这个高密度拾取结果后,需要利用某种过滤手段提取出立体层析所需的、对应于一次反射的运动学信息。杨锴等[8]的策略是先在最小偏移距成像道集内选好数据点,然后直接沿着CIG内已自动搜索好的同相轴信息向大偏移距方向延拓,找出所有大偏移距剖面内的数据点。但对于实际数据,必须注意成像点道集的信噪比可能相当低,对于某一个成像点而言,很有可能从最小偏移距到最大偏移距的RMO信息根本就不连续,仅仅从最小偏移距成像道集出发试图延拓到大偏移距成像道集是不现实的。因此我们针对实际数据从小、中、大偏移距范围内各选择至少一个叠前深度偏移后的叠前偏移距成像道集(至少3个共偏移距成像道集)实施人工拾取(当资料品质较好时,可以只选两个甚至一个偏移距进行拾取;当资料品质很差时,可酌情再多选择几个偏移距成像道集进行拾取),提取出关键目标层的数据点位置;然后从这几个偏移距成像道集上人工拾取的数据点出发,通过其相应的RMO信息(注意这些RMO信息是初始高密度搜索后已经获得的信息),将其延拓到相邻的偏移距成像道集上,从而提取出可靠的、同时高质量的数据点信息。延拓公式如下:
(5)
式中:io代表当前偏移距;do代表偏移距间隔;z代表深度;φ代表在该偏移距处搜索到的倾角信息。显然,这个过程可以理解为对第一轮自动拾取得到的高密度数据点进行带有地质意义的人为过滤,从而挑选出来自关键反射层、对应于一次反射的同相轴的运动学信息。在此基础上,使用挑选出来的数据点实施运动学反偏移,获得来自关键反射层的、对应于一次反射的立体层析数据空间。相对于直接在叠前数据域上使用结构张量算法获得数据点,上述策略显然可以获得更为可靠的立体层析数据空间,因此是一种更为优越的实现方式。技术流程如下:
1) 应用初始速度获得初始偏移成像数据体;
2) 将初始偏移成像数据体视为(X,Z,H)域内的三维数据体,应用三维结构张量实施搜索,同时获得高密度的构造倾角与RMO信息;
3) 在选定的小、中、大偏移距成像道集内进行人工拾取,且仅拾取关键层位处对应于一次反射的成像点;
4) 从人工拾取的成像点位置出发,根据步骤2)获得的RMO信息,根据公式(5)沿偏移距方向往相邻的前后偏移距成像道集进行延拓,获得相邻偏移距成像道集内的成像点位置;
5) 这些挑选后的成像点位置所对应的构造倾角与RMO信息,可从步骤2)获得的高密度运动学信息中检索得到;
6) 基于这些挑选后的成像点位置所对应的构造倾角与RMO信息,实施运动学反偏移(具体计算过程请参阅文献[8]中的公式(8))即可获得挑选后的、更为可靠的立体层析数据空间。
3 理论数据测试
首先基于一个多层背斜盐丘模型理论数据进行测试(图3)。图3a显示了该模型的真实速度与层位分布情况,横、纵向间隔都是10m,横向1201个采样点,纵向601个采样点;图3b是初始立体层析反演速度及反演后获得的反射点分布位置的联合显示,其数据空间信息是按照文献[6]的思路在数据域利用结构张量算法获得的,其初始模型为垂直梯度模型;图3c显示了基于初始反演模型实施Kirchhoff叠前深度偏移获得的初始成像点道集,可以看出成像点道集中对应于浅层的反射同相轴上翘,说明速度还不够精确;图3d 显示了在该成像道集内利用三维结构张量算法搜索得到的高密度成像点位置信息(三维显示,蓝色点代表搜索到的成像点位置信息);图3e显示了1km偏移距成像道集内人工拾取的层位信息;图3f显示了基于1km偏移距成像道集人工拾取的成像点位置以及之前搜索到的RMO信息进行偏移距方向的延拓后得到的成像点位置信息(三维显示,蓝色点代表延拓得到的成像点位置)。可以看到,相比图3d,图3f的成像点位置信息具有明显的地层结构特征,说明利用过滤手段得到了来自关键反射层的、同时也更为优选的、对应于一次反射的成像点位置信息。

图3 基于多层盐丘模型的工作流程测试结果a 真实模型; b 初始反演速度及其数据点位置联合显示; c 利用初始模型得到的成像点道集; d 基于图3b所得成像点道集应用三维结构张量获得的高密度成像点信息(三维显示); e 基于1km共偏移距成像道集人工拾取的对应于一次反射的成像点位置; f 从1km偏移距成像道集拾取的成像点位置出发,基于初始成像点道集信息沿偏移距方向延拓获得的数据点信息(三维显示); g 反偏移后数据点运动学信息与偏移距为1.02km的共偏移距成像道集叠合显示质量控制道集; h 将图3g所示的质量控制道集放大后显示; i 利用挑选后数据点实施反演得到的速度模型; j 基于图3i模型实施叠前深度偏移获得的共成像点道集
图3g显示了根据1.02km偏移距成像道集内挑选后的成像点位置处的构造倾角与RMO信息进行运动学反偏移后获得的数据点运动学信息与1.02km共偏移距成像道集叠合显示的质量控制剖面;图3h为图3g局部放大显示,可以看到反偏移后得到的P参数信息(即同相轴的斜率信息,蓝色细线)与局部同相轴有良好的匹配,证实反偏移算法具有良好的精度。图3i是用挑选后数据点实施立体层析反演得到的速度模型及反射点分布位置的联合显示;图3j为基于图3i模型实施叠前深度偏移获得的共成像点道集,可以看出基于更新的速度模型获得的成像点道集相比之前的初始速度模型偏移的成像点道集更平。
4 二维实际数据算例
二维实际地震数据来自于2011年南海某深水探区采集的数据。测线长约150km,共2900炮,最大偏移距8000m,炮间距50m,检波点间距25m。对反演之前的地震数据做了如下预处理:压制与海面有关的多次波、预测反褶积提高分辨率、12~40Hz带通滤波、利用短时窗自动增益以保证同相轴可以识别并切除了直达波。
首先利用结构张量算法并结合王宇翔等[6]提出的波峰判断准则和线性度准则,在共炮点道集和共检波点道集获得初始立体层析数据空间。如前所述,直接在数据域根据同相性(包括轴的连续性、强振幅性等)拾取的信息,不可避免地会包含绕射波、多次波、侧面波的信息。而这是立体层析中射线正演无法表达的波现象,必然使得反演精度降低。对实际数据反演而言,通过手动拾取的方式将与一次反射无关的无效数据点过滤掉是非常必要的。实际数据测试结果如图4 和图5所示。
图4a是利用结构张量在数据域直接搜索数据点后得到的初始反演速度及反演得到的反射点位置的联合显示;图4b显示了用图4a所示的初始反演速度模型实施叠前深度偏移后得到的部分成像点道集,注意基于该段成像点道集我们应用三维结构张量自动搜索得到了高密度的初始成像点位置信息也显示在该图上(三维显示,蓝色点代表搜索到的成像点位置信息);图4c单独显示了图4b中2km偏移距成像道集上的成像点位置信息,可以看出其密度确实很高。

图4 南海深水某二维测线的测试结果(Ⅰ)a 在数据域进行立体层析反演的初始结果; b基于初始成像点道集自动拾取的成像点位置(三维显示); c 在2km偏移距成像道集内的自动拾取结果; d 在2km偏移距成像道集内人工拾取结果
图4d显示了在2km偏移距成像道集内进行人
工拾取后留下的成像点位置信息。图5a显示了基于图4d所示的2km偏移距成像道集内人工拾取的成像点位置,根据RMO信息进行偏移距方向的延拓后得到的成像点位置(三维显示,蓝色点代表延拓得到的成像点位置信息),相比图4b,过滤后的成像点位置具有清晰的地层结构特征,显然更为准确;图5b显示了将图5a的数据点运动学反偏移后到偏移距为2km时间域共偏移距道集的质量控制;图5c 显示了将图4c所示的初始立体层析数据空间反偏移到偏移距为2km时间域共偏移距道集后的质量控制;对比图5b和图5c可见,原始数据点信息有很多对应于绕射波,而这些数据点对于反演有害无益。

图5 南海深水某二维测线的测试结果(Ⅱ)a 基于2km偏移距成像道集人工拾取层位信息,根据RMO信息在偏移距方向延拓后得到的成像位置点信息(三维显示); b 挑选后的2km共偏移距成像道集内的成像点及其运动学信息被反偏移到2km时间域共偏移距道集; c 挑选前的成像点位置及其运动学信息被反偏移到2km时间域共偏移距道集贴合显示; d 挑选后数据点反演得到的模型; e 利用初始模型实施叠前深度偏移获得的共成像点道集; f 挑选数据点反演模型实施叠前深度偏移获得的共成像点道集; g 利用初始模型获得的叠前深度偏移成像剖面; h 利用挑选数据点后反演模型获得的叠前深度偏移成像剖面
图5d显示了利用过滤后的数据点实施反演得到的速度模型;图5f显示了基于图5d所示速度模型实施叠前深度偏移获得的成像点道集,可以看出该成像点道集相比图5e是用初始速度模型偏移得到的成像点道集,其同相轴的拉平程度有明显改善,表现出速度的反演精度有了进一步提高;图5h显示了基于图5d所示模型实施叠前深度偏移获得的成像剖面,可以看出相比图5g所示的初始速度模型深度成像剖面,不仅主要反射层位的成像深度有明显变化,同时对应于剖面中部深度从3km到6km这一段内幕的刻画亦有明显改善,说明速度反演精度可靠、偏移成像质量有所提高。
5 讨论
从实际数据的应用结果可以看出,在成像域的高密度拾取之后,再用人工拾取的方式从中过滤出具有地质意义的数据点信息,这个技术流程行之有效。由于前期预处理已经做得精细,该实际数据中到了反演阶段已经没有明显的多次波和侧面波干扰。但是依然可以看出,上述流程有效地将绕射波排除在数据空间之外,使得反演精度有了明显提升。另一方面,本方法是一种获取更好数据空间的办法。相比于常规直接在炮数据上拾取,本方法需要依次进行叠前深度偏移、人工拾取和运动学反偏移3个步骤。需要强调的是数据空间的质量是整个立体层析反演的根本,对数据空间质量的要求无论多高都不过分。在数据空间的准备过程中,即便损失一定的效率也是值得的,而且这个操作只需要做一次。总之,本文提出的两步法流程可以获得更佳的立体层析数据空间,虽然相比直接拾取在前期数据空间准备过程中增加了一些计算成本,但能更好地服务于立体层析反演。
本方法适用于虽然叠前炮数据的视觉信噪比不高、但初始叠前深度偏移后依然被能分辨出主要反射波同相轴的地震数据。在此类数据上,本方法有很好的实用价值。因为人工干预可以增加数据的可靠性。完全的人工智能拾取有效反射点的时代尚未到达,我们采取的半自动(自动拾取和手动拾取)是一种折衷但实用的方案。随着人工智能算法的方法发展,通过全自动、免人工干预方式获得最佳数据空间将是未来的研究目标。
6 结论
本文通过理论和实际算例证实了联合结构张量与运动学反偏移的两步法立体层析数据空间提取策略的有效性和合理性。该流程的应用效果很大程度建立在灵活运用结构张量算法的基础上,通过巧妙地将三维结构张量运用于二维叠前成像体的运动学信息搜索,可以同时获得高精度的RMO信息与构造倾角信息,然后在很少几个具有代表性的PSDM后的共偏移距成像道集上进行成像点的拾取,再根据RMO信息进行过滤筛选,即可获得仅与一次反射波有关且与地层格架信息一致的成像点位置信息,保证了在运动学反偏移之后也可以获得与地层格架保持一致的、更为合理的立体层析数据空间。本文方法在南海深水二维测线上的实际应用证实了上述观点。
[1]王华忠,冯波,王雄文,等.地震波反演成像方法与技术核心问题分析[J].石油物探,2015,54(2):115-125
WANG H Z,FENG B,WANG X W,et al.Analysis of seismic inversion imaging and its technical core issues[J].Geophysical Prospecting for Petroleum,2015,54(2):115-125
[2]BILLETTE F,LAMBARÉ G.Velocity macro-modelestimation from seismic reflection data by stereo-tomography[J].Geophysical Journal International,1998,135(2):671-680
[3]BILLETTE F,LE BÉGAT S,PODVIN P,et al.Practical aspectsand applications of 2D stereo-tomography[J].Geophysics,2003,68(3):1008-1021
[4]PRIEUX V,LAMBARÉ G,OPERTO S,et al.Building starting models for full waveform inversion from wide-aperture data by stereo-tomography[J].Geophysical Prospecting,2013,61(S1):109-137
[5]李振伟,杨锴,倪瑶,等.基于立体层析反演的偏移速度建模应用研究[J].石油物探,2014,53(4):444-452
LI Z W,YANG K,NI Y,et al.Migration analysis with stereo-tomography inversion[J].Geophysical Prospecting for Petroleum,2014,53(4):444-452
[6]王宇翔,杨锴,杨小椿,等.基于梯度平方结构张量算法的高密度二维立体层析反演[J].地球物理学报,2016,59(1):263-276
WANG Y X,YANG K,YANG X C,et al.A high density stereo-tomography method based on the gradient square structure tensor algorithm[J].Chinese Journal of Geophysics,2016,59(1):263-276
[7]YANG K,XING F Y.3D stereo-tomography applied to the deep-sea data acquired in the South China Sea,part II:the real case study[J].Expanded Abstracts of 86thAnnual Internat SEG Mtg,2016:16-21
[8]杨锴,熊凯,王宇翔,等.联合结构张量与运动学反偏移的两步法立体层析数据空间提取与反演策略研究Ⅰ:理论[J].石油物探,2017,56(5):694-706
YANG K,XIONG K,WANG Y X,et al,A two-step scheme to extract data space for stereo-tomography based on structure tensor and kinematic de-migration I:theory[J].Geophysical Prospecting for Petroleum,2017,56(5):694-706
[9]王华忠,冯波,王雄文,等.特征波反演成像理论框架[J].石油物探,2017,56(1):38-49
WANG H Z,FENG B,WANG X W,et al.The theoretical framework of characteristic wave inversion imaging[J].Geophysical Prospecting for Petroleum,2017,56(1):38-49
[10]CHAURIS H,NOBLE M S,LAMBARÉ G.Migration velocity analysis from locally coherent events in 2-D laterally heterogeneous media,part I:theoretical aspects[J].Geophysics,2002,67(4):1202-1212
[11]GUILLAUME P,LAMBARÉ G,LEBLANC O,et al.Kinematic invariants:an efficient and flexible approach for velocity model building[J].Expanded Abstracts of 78thAnnual Internat SEG Mtg,2008:3687-3692
[12]VAN VLIET L J,VERBEEK P W.Estimators for orientation and anisotropy in digitized images[J].Proceedings of the first Conference of the Advanced School for Computing and Imaging,1995:442-450

