高可靠性软件定义航空光信息网络的控制器分布优化策略

赵　静, 赵尚弘, 赵卫虎, 李勇军

(1. 空军工程大学信息与导航学院, 陕西 西安 710077; 2. 国防科技大学信息通信学院, 陕西 西安 710106)

0　引　言

航空网络是以空中高速飞行的飞机为空中无线通信的主要节点,以节点间无线通信连接为链路组成的网络,具有覆盖广、高动态、接入量大、任务多样化等特点[1-2]。当前基于机间宽带射频数据链构建的航空骨干网存在带宽资源受限、强电磁干扰环境下通信能力弱等问题,而激光通信链路具有低截获、高速率、抗干扰等特点,是构建航空骨干网络的理想方案。作为未来航空网络的发展方向,基于激光链路的航空骨干网能够连接卫星网络实现大范围空域的综合业务传输,并通过无线射频链路与各类战术子网形成互联互通的通信网络。然而,利用现有的网络技术来构建未来航空网络存在着许多矛盾与挑战,其中最突出的是通用互联网协议(Internet protocol,IP)网络与上层应用多样化特征和需求之间的矛盾[3-4]。

软件定义网络(software defined network,SDN)的出现为解决上述问题提供了契机。SDN将控制平面从传统的路由交换设备中解耦出来,使未来网络中的基础交换设备只具有转发功能,转发平面具有协议无关性、集中化和可编程性。由控制器组成的逻辑上集中控制平面能够检测和采集链路状况和组网信息,具有根据用户需求,对网络资源进行调配的能力,同时具有策略制定和流表项下发功能[5-7]。集中式控制器平面可扩展性较差,易引起连接中断,严重影响网络可靠性,在大规模网络中其性能急剧下降。因此,采用逻辑上集中、物理上分布的控制器部署方式成为未来软件定义航空网络的重要解决方法。控制器部署问题需要考虑两个主要问题,即在网络中部署控制器的数量及部署位置[8-10]。

目前国内外关于控制器部署主要是围绕时延、可靠性、流量处理开销等优化指标来确定的。文献[11]主要解决在给定网络拓扑下,需要多少个控制器以及怎样部署这些控制器这两个问题,通过定义控制器与交换机之间平均/最大传播时延两个指标来分析控制器部署问题。文献[12]以平均时延最短和控制器数量较少为优化目标,采用基于二值粒子群优化算法的方法获得控制器部署问题的非劣最优解集合。文献[13]定义控制路径失效百分比的期望值作为可靠性指标,应用l-w-greedy算法和模拟退火算法解决了SDN中可靠性感知的控制器部署问题。

基于软件定义网络思想,提出了以激光通信链路为骨干互连，以节点间无线通信连接为链路组成的软件定义航空光信息网络的网络架构，分析了软件定义航空光信息网络中控制器部署问题的特点,针对航空光信息网络中的控制器部署问题进行研究,建立了基于网络可靠性的整数规划模型,提出融合人工免疫策略、小生境思想和改进遗传算法的混合优化算法,以实现对基于可靠性模型的优化。最后,以包含34个航空节点的航空网络为仿真场景,考虑了网络中断概率和控制器数量两个瓶颈指标,采用仿真对比实验,验证了本文算法在收敛速度、部署结果方面的性能。

1　软件定义航空光信息网络控制器部署特点

软件定义航空光信息网络根据未来航空信息网络的应用需求,基于软件定义网络的先进思想设计的具有开放可扩展、信息资源高效灵活调度、面向航空服务的新一代航空信息网络,能够为未来航空通信系统提供差异化服务。其主要特点是通过构建具有不同QoS等级的虚拟网络,使得不同等级的航空应用可以根据特定的业务和应用需求选择合适的服务等级,从而实现全网差异化服务,构建灵活高效的新型信息传输模式,极大提高网络通信效能。本文提出了基于SDN技术的航空光信息网络概念,软件定义航空光信息网络的网络架构如图1所示。

图1　软件定义航空光信息网络系统示例

由图1可知,软件定义航空光信息网络主要由3部分组成:①移动子节点,主要包括空中接入节点、地面移动节点等。可通过短波、超短波、无线激光通信等无线通信链路实现多种状态数据的收集和传输。②航空骨干节点,主要包括飞行位置和特性相对稳定的大型飞机平台,通过激光链路构建骨干链路,作为数据接收器接收并传输来自移动节点的状态数据。航空骨干节点同时可作为网络控制器实现对网络的管理与控制。③带内、带外控制信道,能够在移动节点及控制器之间实现控制信息的传输与交换。

特别地,软件定义航空信息网络控制器部署问题具有以下特点:

(1) 节点移动性。航空网络中,节点间相对运动速率大,网络拓扑快速动态变化,同时由于机间激光束对准难度大[14],导致传输节点与控制器的连接中断,进而造成传输节点的不可用,带来航空网络连通性问题。

(2) 节点传输终端故障。受器件性能、传输环境等影响,航空节点上通信终端会发生故障导致该天线资源在某段时间内失效,则在该段时间内与该控制器相连的传输节点需要进行重新安排,这对网络连通性和故障恢复能力带来极大挑战。

(3) 链路传输不稳定性。航空网络中激光链路受大气信道影响严重,大气吸收、散射及光强闪烁效应会造成激光大气衰减效应。微波射频链路容易受到大气中雨、雪、雾等自然状况、路径衰落、多径效应或无线干扰等影响。因此航空链路容易出现频繁的链路中断和重建,具有高误码率、大链路时延等特点[15],这给航空网络的连通性、可用性带来问题。

(4) 三维、大尺度的节点分布特性。航空通信网络中,不同飞机节点的飞行高度存在差异性,飞机节点稀疏分布在大尺度三维空域场景中,导致节点间链路传输时延差异较大。

根据以上分析可知，由于软件定义航空光信息网络中节点运动及链路传输的特点,网络中控制器故障、转发节点及转发链路故障是影响网络性能的重要因素。

2　控制器部署模型

控制器部署是非确定性多项式难(non-deterministic polynomial hard, NP-hard)问题。由上述对软件定义航空信息网络的控制器部署问题特点分析可知,控制器故障、转发节点及转发链路故障是影响软件定义航空信息网络中控制器部署问题的关键,因此可以将该问题看作一类基于网络可靠性的整数规划模型。考虑网络元素的中断概率,对软件定义航空信息网络中控制器分布问题的约束条件作以下描述:

(1) 假设G(V,E)表示网络拓扑,V代表拓扑中网络节点集合,E⊆V×V代表网络节点之间链路的集合,链路权重代表传输时延,设n为网络节点个数,有n=|V|。

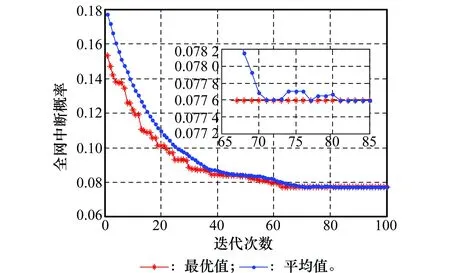
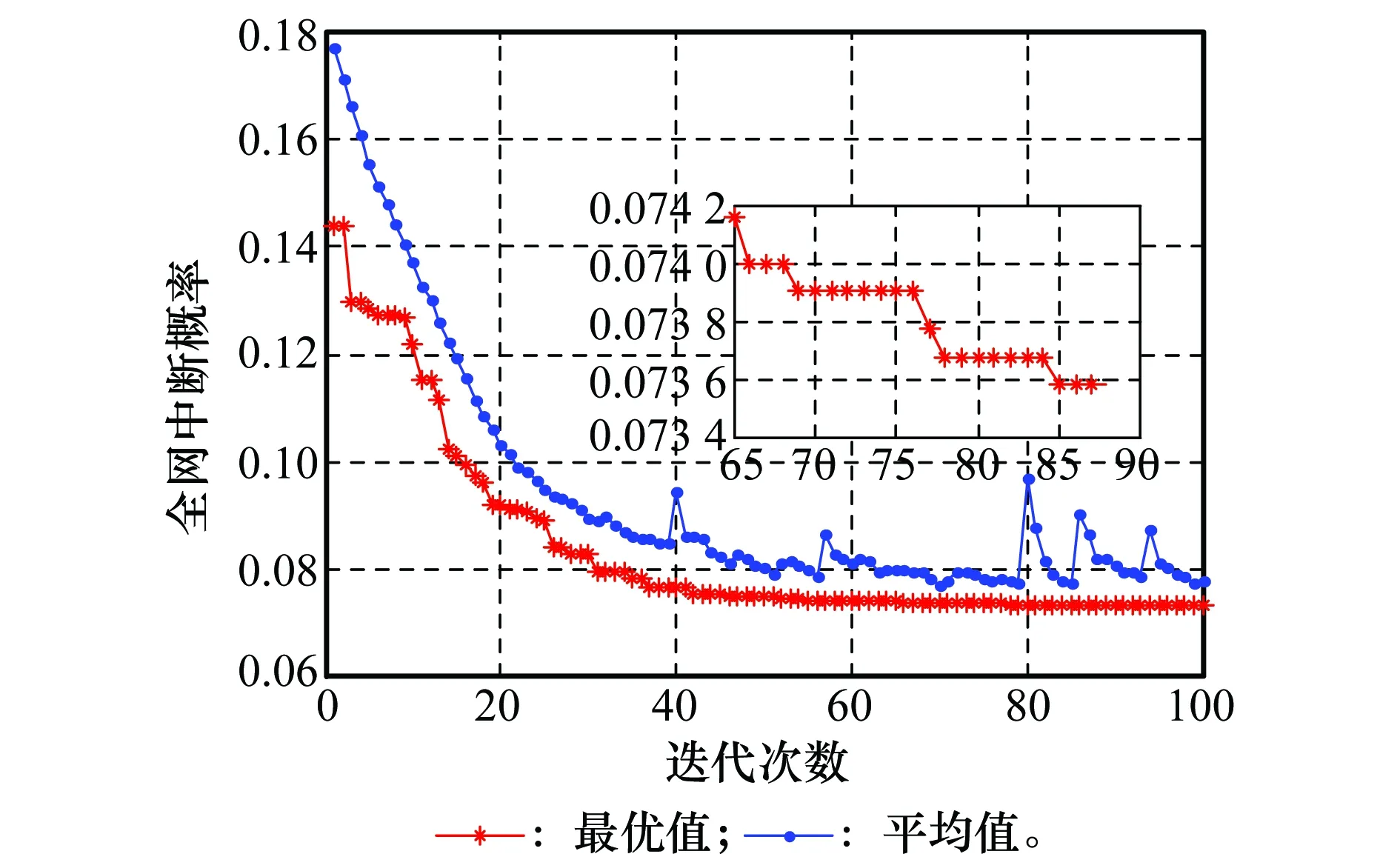
(2) 假设网络节点及链路之间都是独立的。对每一个物理网络元素l∈V∪E,定义pl为元素l的中断概率,0

(3) 给定两个节点s及t,设pathst为从s到t之间的最短路径,假设网络节点与控制器之间的控制路径取最短。

(4) 定义Vc⊆V为控制器可选位置集合。设M⊆Vc代表即将分布在网络中的控制器集合,|M|=k为所需部署的控制器个数。

(5) 交换机与控制器可重复使用同一网络节点,此种情况下,认为二者之间路径的中断概率为0;

(6) 设i∈V,j∈Vc,yj=1代表控制器布置在位置j,否则为0。

(7)xij=1代表yj=1且交换节点i分配给了控制器j,或yi=yj=1且控制器i,j之间有邻接路径,否则为0。设hijl=1代表i与j之间控制路径经过l,否则为0。

优化目标函数是软件定义航空信息网络的全网中断概率。可靠性优化问题模型为

(1)

(2)

(3)

(4)

yi,xij,hijl∈{0,1};∀i∈V,j∈V,l∈V∪E

(5)

3　控制器部署混合优化算法设计

3.1　混合优化算法流程

融合人工免疫策略、小生境思想和改进遗传算法的混合优化算法总流程如图2所示。算法主要由5大函数模块组成,分别为:主函数模块、适应度值计算模块、小生境淘汰模块、精英保留的自适应遗传算法模块和人工免疫模块。

图2　混合优化算法流程

由图2可知，主函数模块主要负责对算法的各类参数进行设置和对遗传过程的控制,最后生成控制器部署序列和目标适应度值。设置的参数包括初始化种群规模及最大遗传代数、自适应交叉和变异参数、及小生境相关参数和免疫记忆库的容量等参数。

3.2　基于精英保留的自适应遗传算法模块

3.2.1问题编码

遗传算法是针对离散问题提出的进化算法,其思想来源于“物竞天择、适者生存”的自然法则,具有很强的全局搜索能力。算法中每个个体代表问题的一个解,称为染色体,解的好坏用适应度值来评价。控制器部署问题的每个可行解即为一个控制器分配方案,每个分配方案Xi有n个决策变量,即染色体的n个基因,代表n个交换节点。每个编码基因Xi=[xi1,xi2,…,xin]代表一种控制器部署方案,xin表示在第i个分配方案中第n个交换节点所选择的控制器。

3.2.2自适应交叉、变异算子

本文设计混合的自适应交叉、变异算子,令Pc和Pm分别为交叉和变异概率。当种群陷入局部最优时,采用小生境淘汰后,新个体可能围绕小生境周边,种群多样性较差。因此,此时选择较大的Pc和Pm可增加新个体的产生,利于跳出局部最优。在算法初始阶段或种群适应度值较分散时,选择较小的Pc和Pm利于保留精英个体,可加快算法的收敛;因此,采用式(6)和式(7)具体计算自适应交叉概率和变异概率。

(7)

式中,参数k1、k2、k3、k4为交叉、变异参数,是0到1之间的变量,其大小在搜索过程中将根据人工免疫模块中“疫苗接种”的情况进行调整,具体调整方法如式(10)所示。favg为种群的平均适应度值,fmin为种群的最小适应度值,fc为交叉个体平均适应度值,fm为要变异个体的适应度值。

3.2.3精英保留策略

传统遗传算法中个体被选择的概率与个体适应度值呈正比,通常需要对目标值进行调整后作为适应度值,而调整不当将影响算法的性能。为克服此不足,采用精英保留策略的遗传算法,将每代最优秀的部分个体直接遗传到下代。因此适应度函数只需反映个体的优劣,直接采用目标值即可。由于个体适应度值的计算量较大,因此需充分利用已完成计算的个体;并且采用小生境淘汰可能降低算法的收敛速度。选择时将父代个体与子代个体合并为大种群,将其最优的一半种群个体直接保留到下代,参与下代竞争,并将这部分精英个体作为父代以产生新个体。因此,直接保留的精英个体适应度值不需再计算,从而节省了计算资源,加快了收敛速度。

3.3　小生境思想

为避免种群聚集在局部最优值附近,以保持种群多样性,提高算法搜索效率和全局优化能力,算法引入小生境思想,采用动态变化的小生境距离参数,对搜索到最优值附近的次优个体进行惩罚,从而减小聚集在局部最优值附近个体被选择到下一代的概率。

定义1设个体Xi与种群中所有个体的最小欧氏距离为其与种群的差异Di,即

i=1,2,…,Nscale

(8)

式中,变量Nscale为种群规模。

定义2设Nniche个最优个体与种群中平均差异为种群的小生境距离L,当平均差异小于1时,取小生境距离L=1,即

(9)

3.4　人工免疫模块

(1) 疫苗接种

传统遗传算法在收敛到局部最优值的搜索后期,会频繁产生曾经搜索过的个体,不但浪费计算资源,耽误计算时间,还将造成算法寻优能力的下降。针对此问题,本文借鉴人工免疫算法思想,将历史搜索过的较优个体记忆成“抗体”,产生的新个体视作“嫌疑抗原”,经过新个体与系统接种的“疫苗”比对,消除其嫌疑或将其定性为“抗原”,则分别采取“释放”或“吞噬”操作。当进行“吞噬”操作后,采用“免疫克隆”方法重新产生新个体来替代这个个体。在产生新个体时,采用式(6)和式(7)计算自适应交叉、变异概率。

在搜索过程中一旦出现重复个体,则将当前种群放入“免疫记忆库”，随着搜索的进行,用搜索到的较优个体更新“记忆库”中最差的个体。在“疫苗接种”过程中,需要将新个体与“抗体”对比,若直接逐个比较,计算量大。因此,将记忆库中的个体(免疫知识)进行整理,建立记忆库个体基因的索引;当新个体与之比较时,可采用“二分法”检索,则计算量将成指数级减少。

(2) 自适应参数调整

在“疫苗接种”过程中,根据本代种群个体的重复率,调整自适应遗传算法中的交叉、变异参数。当重复个体较多时,放大交叉、变异参数以增加种群的多样性,减少重复个体的出现,交叉、变异参数更新公式为

(10)

式中,变量β为放大因子,取值范围为1到2之间(通常取1至1.1之间小数),β越大，变异参数放大得越快,在仿真分析中一般根据经验给定变量β取值。

4　仿真及结果分析

为了验证算法的有效性,采用34个节点的航空网络拓扑,对于每个节点标号,假设每个节点均可放置交换机,控制器部署在交换机的位置上。在航空网络拓扑中,采用时延作为链路的权重,链路权重为[1,10]的均匀随机数;为了保证网络连通性,采用网络组件故障率较小的网络场景,设单个节点和链路的中断概率为区间[0,0.02]和[0,0.04]的随机数[16-17]。实验仿真分别采用标准的遗传算法和本文提出的混合优化算法对问题进行寻优,对比分析两算法的搜索过程。设置两算法的种群规模Nscale=80,迭代次数为100,根据多次重复试验,将自适应交叉、变异参数初始值分别为0.5、0.25、0.05、0.025,放大因子β=1.05。

当控制器数量取k=6时,标准的遗传算法和混合优化算法的搜索结果如图3、图4所示。

图3　标准遗传算法搜索过程

图4　混合优化算法搜索过程

由图3和图4的对比单次实验可知,标准遗传算法搜索到的最优值是0.077 6;而混合优化算法的最优值是0.073 6,明显优于标准遗传算法。由图3、图4搜索中期局部放大图可知,标准遗传算法在60代左右已完全收敛,最优值保持不变;本文提出的混合优化算法在60代基本收敛之后,最优值还出现了多次小幅度的跳跃,表明混合优化算法在收敛之后仍然能够跳出局部极值,搜索到更优解。对比两图的最优值和平均值曲线可知,到搜索后期标准遗传算法的种群均值与最优值趋于一致,表明种群个体相似度极高,大部分个体聚集在最优值附近,这是由于标准遗传算法的多样性较差。而混合优化算法的种群均值与最优值存在较大差距,表明混合优化算法引入小生境思想和自适应遗传算子提高了种群的多样性。

为了验证本文算法的有效性,在图5中给出了不同控制器数量条件下,标准遗传算法和本文提出混合优化算法所得到的部署结果。对每组算例(即在每个控制器个数条件下)进行100次仿真,得到每次仿真的最优值作为该次仿真结果,再对多次仿真结果求取均值,得到不同控制器数量条件下全网中断概率如图5所示。

图5　中断概率随控制器数量的变化

由图5可知，优化目标值,即全网中断概率随着控制器数量的变化,代表了某个控制器数量环境下,算法优化部署的有效性。该优化目标值越小,表示部署方案的效果越好。当控制器数量为2～7时,在图5中分别标出了两种算法得到的优化结果数值。由图5可知,在不同的控制器数量条件下,本文提出的混合优化算法得到的部署方案结果均优于标准遗传算法,特别地,当控制器数量大于6,混合优化算法的寻优结果表现出明显的优势。这是由于两种随机搜索算法,在有限的迭代过程中标准遗传算法找到最优值的概率较低,而混合优化算法引入小生境和人工免疫思想,在算法收敛后具有主动改进算法多样性的策略和跳出局部极值的操作,表明此算法适用于处理此类NP-hard问题。

当控制器数量分别为4、8、12时,采用混合优化算法的算法收敛性能,其中全网中断概率为每代最优值,其随迭代次数的变化情况如图6所示。算法种群规模Nscale=80,迭代次数为150。

图6　不同控制器数量下中断概率随迭代次数的变化

由图6可知,随着控制器数量的增加,算法收敛时间变长,收敛速度变慢。特别地,当控制器个数为4时,算法在50代左右基本收敛,而当控制器数量增加到k=8和k=12时,算法迭代至100代和110代左右基本收敛。这是因为控制器数量增加,控制器部署方案的多样性增加、相应的方案数量增加,因此收敛到较优方案的时间增加。

5　结　论

提出软件定义航空光信息网络中基于网络可靠性的控制器部署策略,利用融合人工免疫策略、小生境思想和改进遗传算法的混合优化算法,在满足网络性能的条件下,为确定在网络中部署多少个控制器以及如何部署控制器提供了可行方案。该策略以网络中断概率为评价指标,算法优化目标是全网中断概率最小,应用混合优化算法进行迭代进化,得到了最终的优化解集,由此得到了网络中不同控制器数量条件下的最优部署方案。由于控制器部署会影响软件定义航空信息网络的诸多方面,下一步将针对控制器部署问题的多类评价指标,如时延、流量、负载均衡等参数展开研究,提出相应的控制器部署策略。

参考文献：

[1] KWAK K, SAGDUYU Y, YACKOSKI J, et al. Airborne network evaluation: challenges and high fidelity emulation solution[J]. IEEE Communications Magazine, 2014, 52(10): 30-36.

[2] SCHNELL M, EPPLE U, SHUTIN D, et al. Future aeronautical communications for air-traffic management[J]. IEEE Communications Magazine, 2014, 52(5): 104-110.

[3] MENDONCA M, ASTUTO B, NGUYRN N, et al. A survey of software-defined networking: past, present, and future of the programmable networks[J]. IEEE Communication Surveys and Tutorials, 2014, 16(3): 1617-1634.

[4] 王俊, 陈志辉, 田永春, 等.软件定义网络技术在战术通信网中的应用研究[J]. 通信技术, 2014, 47(12): 1392-1399.

WANG J, CHEN Z H, TIAN Y C, et al. Application of software-defined network technology in tactical communication network[J]. Communications Technology, 2014, 47(12): 1392-1399.

[5] AGUADO A, LOPEZ V, MARHUENDA J, et al. ABNO: a feasible SDN approach for multivendor IP and optical networks[J]. IEEE/OSA Journal of Optical Communications & Networking, 2015, 7(2): A356-A362.

[6] OLIVEIRA B T D, GABRIEL L B, MARGI C B. TinySDN: enabling multiple controllers for software-defined wireless sensor networks[J]. IEEE Latin America Transactions, 2014, 13(11): 3690-3696.

[7] MATIAS J, GARAY J, TOLEDO N, et al. Toward an SDN-enabled NFV architecture[J]. IEEE Communications Magazine, 2015, 53(4): 187-193.

[8] LANGE S, GEBERT S, ZINNER T, et al. Heuristic approaches to the controller placement problem in large scale sdn networks[J]. IEEE Trans.on Network & Service Management, 2015, 12(1): 4-17.

[9] ROS F J, RUIZ P M. On reliable controller placements in software-defined networks[J].Computer Communications,2016,77:41-51.

[10] VOCHIN M, BORCOCI E, AMBARUS T. On multi-controller placement optimization in software defined networking based WANs[C]∥Proc.of the 14th International Conference on Networks, 2015: 261-266.

[11] HEELER B, SHERWOOD R, MCKEOWN N. The controller placement problem[C]∥Proc.of the Workshop on Hot Topics in Software Defined Networks, 2012: 7-12.

[12] 王丽霞,曲桦,赵季红.软件定义网络中应用二值离子化优化的控制器部署策略[J].西安交通大学学报,2015,49(6):67-71.

WANG L X, QU H, ZHAO J H. A strategy of controller placement in software defined networks using binary particle swarm optimization[J]. Journal of Xi’an Jiaotong University, 2015, 49(6): 67-71.

[13] HU Y N, WANG W D, GONG X Y, et al. Reliability-optimized controller on placement for software-defined networks[J]. China Communications, 2014, 11(2): 38-54.

[14] Oppenhauser G. In orbit test result of an operational optical inter-satellite link between ARTEMIS and SPOT4, SILEX[J]. Proc.of SPIE-the International Society for Optical Engineering, 2002, 4635:1-15.

[15] CHENG B N, CHARLAND R, CHRISTENSEN P, et al. Evaluation of a multihop airborne IP backbone with heterogeneous radio technologies[J]. IEEE Trans.on Mobile Computing, 2014, 13(2): 299-310.

[16] LI X, NAHRSTEDT K. Reliability models and evaluation of internal BGP networks[C]∥Proc.of the 23rd Annual Joint Conference of the IEEE Computer and Communications Societies, 2004: 1593-1604.

[17] HU Y N, WANG W D, GONG X Y, et al. On the placement of controllers in software-defined networks[J]. Journal of China Universities of Posts and Telecommunications, 2012, 19(9): 92-97.