基于维修重要度的多态系统预测性维修

江秀红, 段富海, 胡爱玲

(1. 沈阳航空航天大学电子信息工程学院, 辽宁 沈阳 110036; 2. 大连理工大学传感测控研究所, 辽宁 大连 116024)

0　引　言

预测性维修(predictive maintenance,PdM)是包含状态监测、历史统计信息、专家经验等的复杂系统工程。设计良好的PdM可提高系统可靠性、有效性和安全性,降低故障间隔时间[1-2]。

多态系统(multistate system,MSS)各单元间相互作用影响[3-4]。MSS的失效受到多方因素影响,如单元的连接方式、工作的时序及失效的顺序等。目前PdM研究对象大多为具有简单拓扑结构(串联、并联、混联等)的二态系统[5],且制定的维修策略多是静态的[6-10],未能体现系统运行过程中受到的各工作应力及环境应力对维修策略的影响。有些研究虽讨论了具有复杂结构系统的维修策略或维修模型[11-12],但对具有桥式、表决等连接关系的MSS,在实际应用中仍显不足。

对系统中各单元的重要性进行分析评估也是维修策略制定过程中非常重要的一项内容。重要性分析可以识别系统的脆弱点,量化单元的临界重要度,评价系统中特定单元对系统的影响程度。二态单元的重要性分析已有若干讨论和成功应用。与传统二态系统重要性分析相比,对MSS进行重要性分析研究更贴合实际工程需求[13-14]。 针对MSS内多态单元的各种重要性分析又称为重要度分析,逻辑微分是多值逻辑(many-valued logic,MVL)中的一种数学方法[15-16],目前许多多态单元的重要度都是基于此提出的,如结构重要度(structure importance,SI)、Birnbaum重要度(Birnbaum importance,BI)、临界重要度(critical importance,CI)、可靠性增加当量(reliability add weight,RAW)等。

本文将首先讨论多态单元重要性评价存在的不足,进而提出多态单元维修重要度(maintenance importance,MI)的概念及相应计算方法。接着提出利用目标导向(goal-oriented，GO)法[17-18]和MI搭建综合可靠性评估、单元MI评价和维修策略制定为一体的预测性维修平台,为后续维修活动的实施和维修策略的进一步优化提供支撑信息。最后通过某捷联惯导系统算例,验证了所提MI以及预测性维修平台的可行性和有效性。

1　面向维修的重要度评价——MI

1.1　现有多态单元重要度评价存在的不足

几种基于逻辑微分的成熟多态单元重要度分析方法,仍存在如下几点不足:

(1) 几种重要度算法都是基于系统的结构函数或状态概率进行的近似静态分析。这里的静态指的是只依据当前的结构函数和状态概率值,从系统的结构函数逻辑表里选取某些状态组合项进行计算,并未考虑到单个单元状态概率的改变对系统性能的影响。

(2) 几种重要度算法在应用逻辑微分的过程中,均假设系统和单元的性能水平不能过快地改变,状态前后是有序的。这种假设在有些情况下是合适的,例如具有退化性能的机械单元、汽车轮胎的磨损。但实际中还有许多系统和单元的性能状态并不是有序的,最常见的就是各类电子元器件,例如具有短路、断路和正常3种工作状态的二极管,短路和断路状态间就没有先后顺序。

(3) 几种重要度算法在计算过程中都要求提供完整的系统结构函数逻辑表,这就造成了这些算法对系统的复杂程度都比较敏感。例如一个8单元MSS,单元和系统都具有4个状态,则形成的系统结构函数状态逻辑表中将有48=65 536个不同组合项,这无疑将使IM的计算过程变得异常繁琐甚至无法完成。由于系统级可靠度函数的显式通常难以获得,所以这些重要度在实际中应用中受到了很多限制。

(4) 几种重要度算法在处理MSS中单元重要度时,考虑的均是单元状态改变对系统完美工作或完全失效的影响,并未考虑对系统中间过渡状态的影响。

(5) 几种重要度算法的主要目的均是找出对MSS性能水平影响最大和最小的系统单元,以便为系统设计和开发阶段的行为提供指导意见。但在复杂系统运行过程中,有时需要确定哪些单元需要维修,按什么样的顺序进行维修,更关心单元维修后对系统可靠度提升的程度、单元的失效率以及维修成本等。

基于以上不足,下面引入一种新的多态单元重要度评价方法——MI。

1.2　MI

MI的提出借鉴了故障树分析中的概率重要度、故障模式危害度以及多态单元的BI,目的是基于系统的实时运行情况,综合权衡影响单元维修的各项指标,定量评估单元重要性,以便为后续维修活动中单元的维修顺序提供支撑信息。

MI主要由3项评价指标构成,U={风险度,检测度,贡献度}。“风险度”即不可靠度,表明单元在区间[0,t]内不能正常工作的概率。多态单元由于存在多种性能状态,分析单元风险度时需根据多态的划分区别对待。若状态N为完全失效状态,1为完美工作状态,2～N-1为介于成功和失效的中间性能状态,且可靠性为性能水平j的概率,即

(1)

则单元i的风险度v1,i(t)可定义为

(2)

风险度即为系统完全不能工作的概率。若2～N-1表示单元i独立的N-2个故障模式,则风险度可定义为

(3)

此时MSS的风险度为除去系统完美工作的所有状态概率之和。

“检测度”是单元测试性、维修度和维修费用的综合评价,可根据经验模糊确定,用v2,i(t)表示t时刻单元i的检测度。

i=1,2,…,n;l=1,2,…,N-1

(4)

单元i对系统整体性能提升的贡献度为

(5)

式中,al为权重系数,可根据系统各状态的重要性来合理设置。假设系统有n个单元,则维修评价矩阵VM可表示为

(6)

式中,vij表示系统构成单元i在维修评价因素U下的评估值。评价指标的权重对MI的可信度影响较大,可采用层次分析法(analytic hierarchy process,AHP)来确定。首先根据决策目标、评价标准和决策对象间的关系,将整个决策系统分为最高层、中间层和最底层,建立层次结构图。然后参考专家意见,构造3个评价指标的判断矩阵,用1～9标度方法给出。若判断矩阵的一致性检验通过,则利用一定的数学方法,如特征根法、和法、根法、幂法等,进行层次排序,计算各评价指标的权重。

2　基于MI的PdM

GO法是一种以成功为导向的系统可靠性分析技术,其建立的系统可靠性模型称作GO图。GO图通过GO操作符表征系统各单元及单元间的逻辑关系,GO操作符具有状态值和状态概率两个属性,而状态概率的确定又与单元寿命分布模型有直接关系。因此,系统工作过程中受到的各种应力可通过寿命模型反映到GO操作符的状态概率上。基于GO法和MI的PdM流程如图1所示。

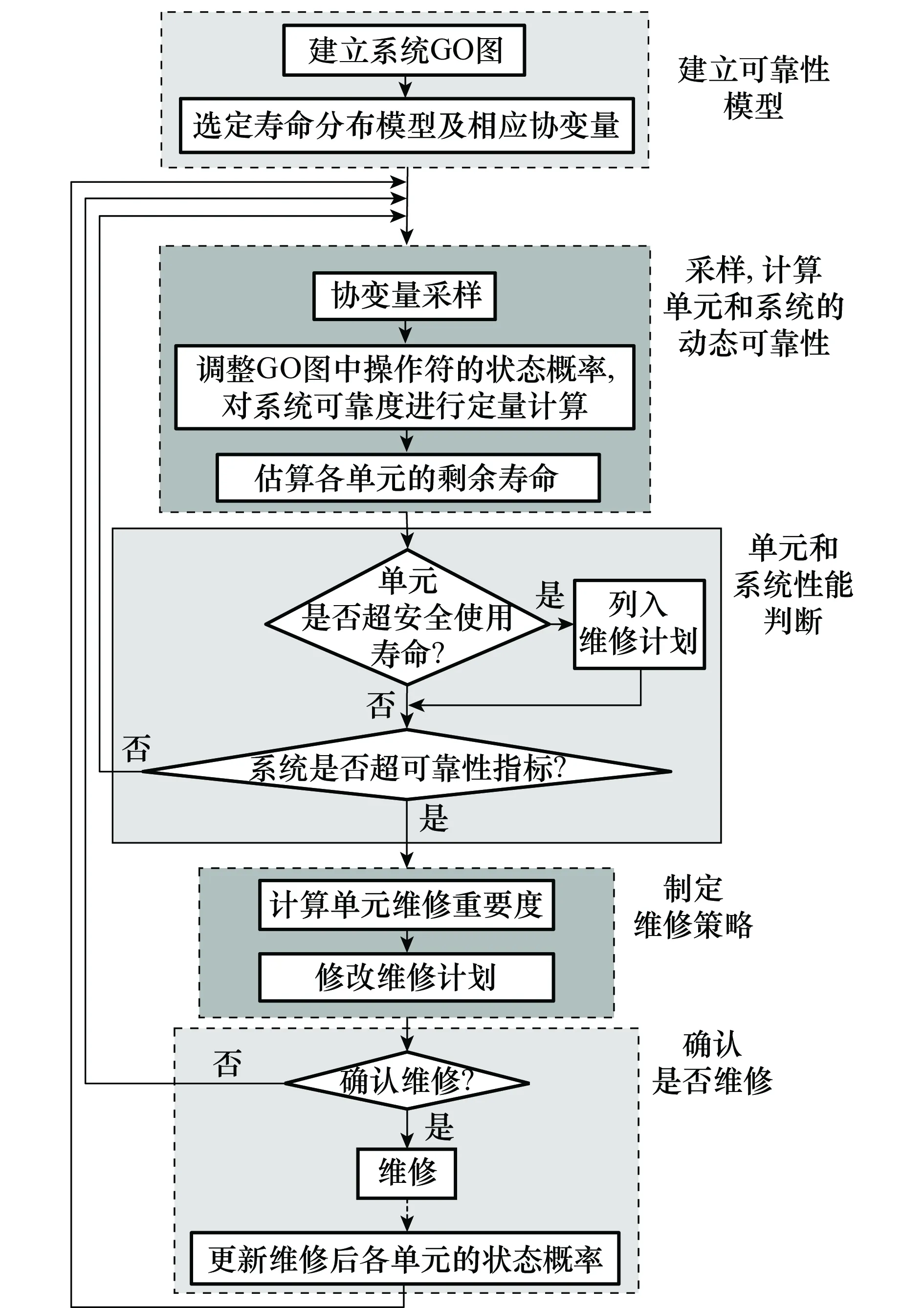
图1　基于GO法和MI的PdM流程

整个PdM流程分5步:

步骤1利用GO法建立系统可靠性模型GO图,并根据单元寿命分布模型确定GO操作符的状态值和状态概率函数。

步骤2在Simulink下建立系统可靠性仿真平台,设定采样间隔,每采样一次,GO操作符的状态概率则更新一次,估算各单元剩余寿命,并沿信号流流向计算系统可靠度。

步骤3判断单元是否超寿,系统可靠度是否低于设定阈值。

步骤4若系统不满足可靠性指标要求,则计算单元维修重要度,并根据MI的大小制定维修策略。

步骤5若确认维修,则更新维修后各单元的状态概率值。

3　捷联惯导系统算例验证

以某捷联惯性导航系统为例,对本文所提的算法进行验证,系统GO图如图2所示。图2中圆圈和三角形为不同类型的操作符,模拟系统中不同的单元。图形内的两个数字分别表示该操作符的类型和编号,比如“2-5”类型为2(两状态操作符),编号为5;“18-6”类型为18(多态操作符),编号为6。各操作符状态间的转移率如表1所示。

图2　某捷联惯导系统的简化GO图

编号单元状态转移率(单位时间h)λi,0λi,2λi,31,2主备电源1.2×10-5—1.8×10-53,4主备电子线路——1.5×10-56-9陀螺1～44.2×10-51.3×10-52.0×10-511-16加速度计1～67.8×10-53.4×10-51.4×10-519,20采集板1,2——2.0×10-521,22导航计算机1,2—4×10-64×10-624控制显示台—2×10-65×10-6

为专注于算法验证,作如下假设:

假设1单元寿命分布采用恒定故障率模型;

假设2维修资源是充足的;

假设3在一个任务剖面中,不考虑停机维修,只根据系统运行状态调整维修策略;

假设4根据系统完美工作概率ps,1(t)将维修分为两级,1级:0.9≤ps,1(t)<0.99,系统偶然会发生故障,建议维修;2级:ps,1(t)<0.9,系统很可能会发生故障,强烈建议维修。

根据专家经验,设定风险度、检测度、贡献度的判断矩阵A为

矩阵A的最大实特征根λmax=3.009,经一致性检验,一致性比率约为0.08,可以接受。接着计算A中每一列元素之和,并将各元素除以其所在列的元素和,得到新的矩阵A′。然后计算A′中每一行元素的平均值,该平均值即为该行对应评价指标的权重系数。各评价指标的权重计算结果为

最后对ω进行数值归一化,得到3个评价指标,则最终权重ω=[0.540.300.16]。

假设系统采样间隔Δt=1 h,单元的可靠度阈值RC均为0.85。随着运行时间t的增大,单元和系统可靠度逐渐降低,系统完美工作概率(即可靠度函数ps,1(t))输出曲线如图3所示。

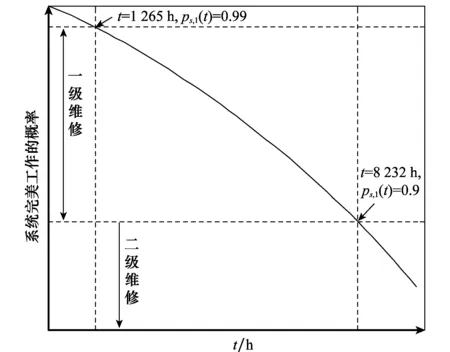
图3　系统完美工作的概率曲线

可见,当t≥1 265 h时,ps,1(t)<0.99,系统进入1级维修范围,建议维修;若一直未采取任何维修措施,当t≥8 232 h时,ps,1(t)<0.9,维修级别提高到2级,强烈建议维修。若计划执行维修,则需利用综合评价法计算维修时刻各单元的维修重要度,以确定维修顺序。t=1 265 h时各单元维修重要度的评判结果如表2所示(冗余单元具有相同结果)。

风险度、贡献度利用动态仿真平台获得,检测度则由专家模糊给定。由表2可见,t=1 265 h时,综合权衡各单元对系统的风险度、检测度以及贡献度,单元的维修优先级从高到低依次为:控显台、加速度计、采集板、电源、电子线路板、陀螺、导航计算机。

表2　单元维修重要度的评判结果(t=1 265 h)

需要注意的是,虽然加速度计的剩余寿命最少,“风险度”和“检测度”也较高,但由于其是多冗余配置(6取3),单个性能的改善对系统可靠性提升的能力有限,因此其贡献度在所有单元中是最低的(仅有2.543×10-12),导致其维修重要度(0.058 9)并不是最高的。同样,陀螺是4取2的冗余配置,贡献度较低,加上检测度又最低(0.02),所以其维修重要度很低。控制显示台不存在冗余,是系统关键单元,失效将导致系统直接失效,因此控显台的贡献度与其他单元不是一个数量级(7.871×10-1),最终其维修优先级别也最高。

表3　单元维修重要度的评判结果 (t=8 232 h)

由于t=8 232 h时部分单元已超出其安全工作范围,所以对维修重要度排序时需分两批进行。电源、陀螺、加速度计和采集板在t=8 232 h时剩余寿命为0,必须进行维修,在第一批次中进行排序。其余单元尚有剩余寿命,在第二批次中进行排序。需要注意的是,表3中显示部分单元的剩余寿命预测值为0,并不是说这些单元失效不能工作了,而是指其在该时刻超负荷工作,已超出了其安全工作范围(也即单元可靠度低于设定阈值,需要采取维修措施。

维修时,第1批次的单元必须采取维修措施,第2批次的单元按照维修顺序有选择地进行维修。由表3还可见,加速度计对系统贡献度最小,所以维修3个加速度计后,系统可靠性基本没有改善。同样,电源和电子线路对系统的贡献度也较小,其维修对系统可靠度的提升程度也有限。控显台对系统贡献度最大,所以当维修范围包含控显台后,系统可靠度将比上一维修范围的可靠度提升了约6%。

图4给出了t=1 265 h和t=8 232 h各单元维修优先级对比。

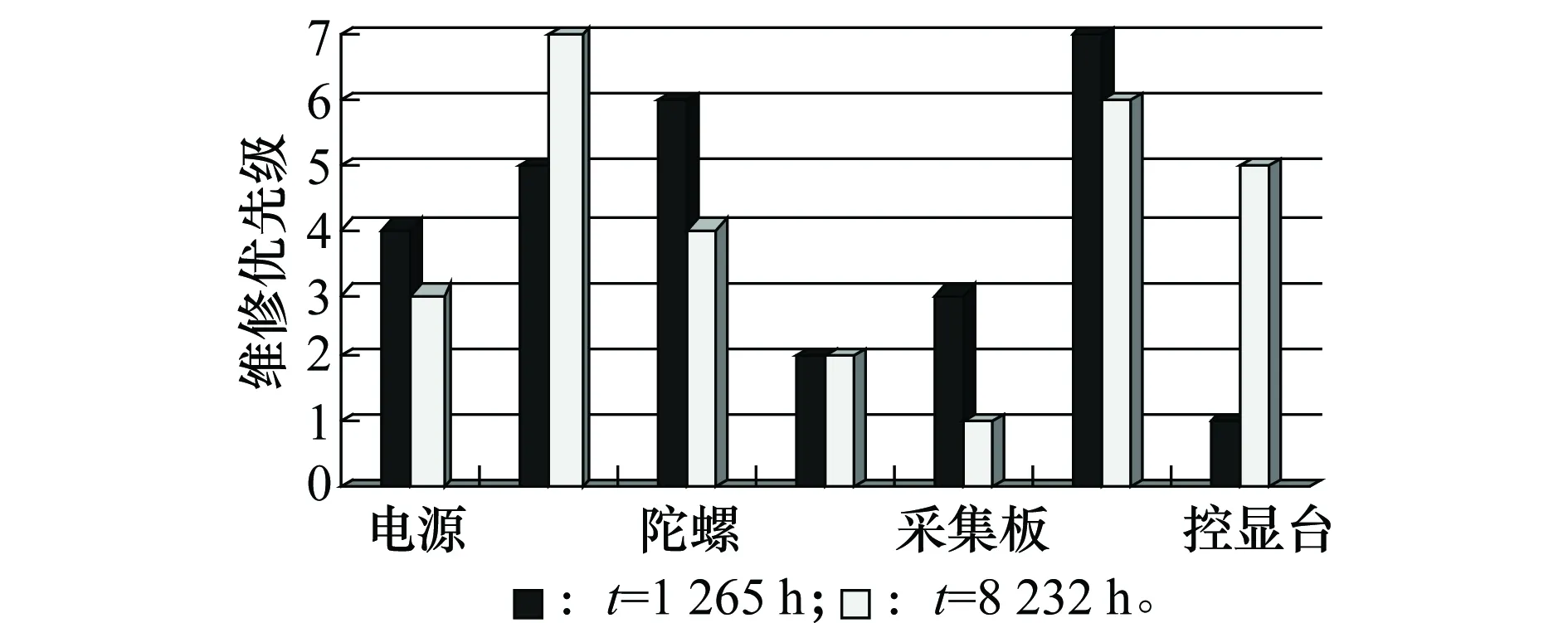
图4　不同时刻单元维修优先级的对比

由图4可见,各单元维修级别并不是一成不变。最明显的就是控显台,t=1 265 h时其优先级别最高,但t=8 232 h时由于部分单元超出了安全工作范围,需要优先维修,控显台的维修优级别下降到5。

4　结　论

对MSS的PdM展开了研究。首先讨论了基于逻辑微分的几种常用多态单元重要度的不足;接着从维修的角度,通过综合权衡各单元风险度、对系统可靠性的贡献度、检测度3个指标来量化单元的维修顺序,提出维修重要度的概念,根据其大小确定单元维修的优先级。其次基于GO法搭建了一个综合可靠性评估、单元维修重要性评价为一体的分析平台。考虑到冗余单元的存在,只有当预测到系统可靠度低于设定阈值时,才根据单元的维修重要度和剩余寿命提出维修计划,以减少不必要的预防性维修,增加系统可用性。最后以某捷联惯导系统为例,计算出了系统各单元在不同维修时刻的维修优先级,为后续维修活动中单元的维修顺序和维修策略的制定提供了有力的支撑信息。

参考文献：

[1] 贾云献,李欣玥,王鹏,等.考虑多故障模式的新型装备更新保修费用预测[J].系统工程与电子技术,2015,37(8):1810-1817.

JIA Y X, LI X Y, WANG P, et al. Cost predictive of the renewing warranty policy considering multiple failure modes for new equipment[J].Systems Engineering and Electronics,2015,37(8): 1810-1817.

[2] BABAN C F, BABAN M, SUTEU M D. Using a fuzzy logic approach for the predictive maintenance of textile machines[J]. Journal of Intelligent and Fuzzy Systems,2016,30(2):999-1006.

[3] 周丰旭,李爱平,谢楠.基于性能衰退的多态制造系统可靠性分析[J]. 计算机集成制造系统, 2014, 20(6): 1424-1431.

ZHOU F X, LI AI P, XIE N. Reliability analysis of multi state manufacturing systems based on performance degradation[J].Computer Integrated Manufacturing Systems,2014,20(6):1424-1431.

[4] 古莹奎, 承姿辛, 李晶. 性能水平划分下的多状态系统可靠性分析[J]. 中国安全科学学报, 2015, 25(5): 68-74.

GU Y K, CHENG Z X, LI J. Reliability analysis of multi-state system under performance level division[J]. China Safety Science Journal, 2015, 25(5): 68-74.

[5] COMPARE M, ZIO E. Risk sensitive particle filtering in support of predictive maintenance[J]. Chemical Engineering Transactions, 2013, 2013(33): 307-312.

[6] NGUYEN T P K, BEUGIN J, MARAIS J. Method for evaluating an extended fault tree to analyse the dependability of complex systems: application to a satellite-based railway system[J]. Reliability Engineering and System Safety,2015,2015(133):300-313.

[7] VAN P D, BARROS A, BéRENGUER C. Dynamic grouping maintenance with time limited opportunities[J]. Reliability Engineering and System Safety, 2013, 2013(120): 51-59.

[8] MAHMOOD S, MAXIM F. An optimal age-based group maintenance policy for multi-unit degrading systems[J]. Reliability Engineering and System Safety, 2015, 2015(134): 230-238.

[9] MAJID F E, NEZAM M A. An efficient algorithm for the multi-state two separate minimal paths reliability problem with budget constraint[J].Reliability Engineering and System Safety,2015,2015(142): 472-481.

[10] ZHANG X N, LU X Y. Multi-state system reliability assessment based on Bayesian networks[J].Computer Modeling and New Technologies, 2014, 18(8): 31-38.

[11] PENG R, XIE M, NG S, et al. Element maintenance and allocation for linear consecutively[J].IIE Transactions,2012,44(11): 964-973.

[12] VU H C, DO P, BARROS A,et al.Maintenance grouping strategy for multi-component systems with dynamic contexts[J]. Reliability Engineering and System Safety, 2014, 2014(132): 233-249.

[13] VAN NOORTWIJK J M. A survey of the application of Gamma processes in maintenance[J]. Reliability Engineering and System Safety, 2009, 94(1): 2-21.

[14] ZAITSEVA E, LEVASHENKO V. Importance analysis of multi-state system based on structural function methods[C]∥Proc.of the European Safety and Reliability Conference, 2012: 2152-2158.

[15] VAN P D, BARROS A, BéRENGUER C. Reliability importance analysis of Markovian systems at steady state using perturbation analysis[J]. Reliability Engineering and System Safety, 2008, 93(11): 1605-1615.

[16] ZAITSEVA E, PUURONEN S. Representation and estimation of multi-state system reliability by decision diagrams[C]∥Proc.of the Joint ESREL and SRA-Europe Conference: Safety, Reliability and Risk Analysis: Theory, Methods and Applications, 2009: 1995-2002.

[17] 金霞,段富海.基于GO法的电动静液作动器可靠性分析[J].大连理工大学学报,2013,53(6): 846-850.

JIN X, DUAN F H. Reliability analysis of electro hydrostatic actuator based on GO methodology[J].Journal of Dalian University of Technology,2013,53(6): 846-850.

[18] 刘林林,任羿,王自力,等.基于贝叶斯网络的GO法模型算法[J].系统工程与电子技术,2015, 37(1): 212-218.

LIU L L, REN Y, WANG Z L, et al. Algorithm based on Bayesian networks for GO methodology[J]. Systems Engineering and Electronics, 2015, 37(1): 212-218.