起点低 立意新 蕴意深*——2017年江苏省南京市数学中考题第22题评析

●　　　(东庐初级中学,江苏 南京　211200)

2017年江苏省南京市数学中考题第22题的尺规作图，可谓考法新颖.一般尺规作图的考法是预先给出一些条件，按要求作出具备这些条件的图形.而本题让学生通过尺规作图判断一个角是否为直角，并用文字说明，这其中渗透了图形语言、文字语言、符号语言的相互切换.试题要求用两种不同的方法，具有创新性，意在通过一题打通几何各板块的知识，需要学生的深度思考，以及在平时的解题过程中，注重经验的积累．

1　试题的呈现及参考答案

1.1试题的呈现

题目“直角”在初中几何学习中无处不在.如图1，已知∠AOB，请仿照小丽的方式，再用两种不同的方法判断∠AOB是否为直角(仅限用直尺和圆规).

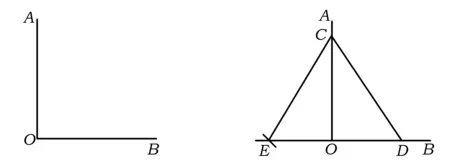
图1　　　图2

小丽的方法：如图2，在OA,OB上分别取点C,D，以C为圆心、CD长为半径画弧，交OB的反向延长线于点E，若OE=OD，则∠AOB=90°.

(2017年江苏省南京市数学中考试题第22题)

1.2试题的参考答案

方法1如图3，在射线OA，OB上分别截取OC=4，OD=3，若CD=5，则∠AOB=90°．

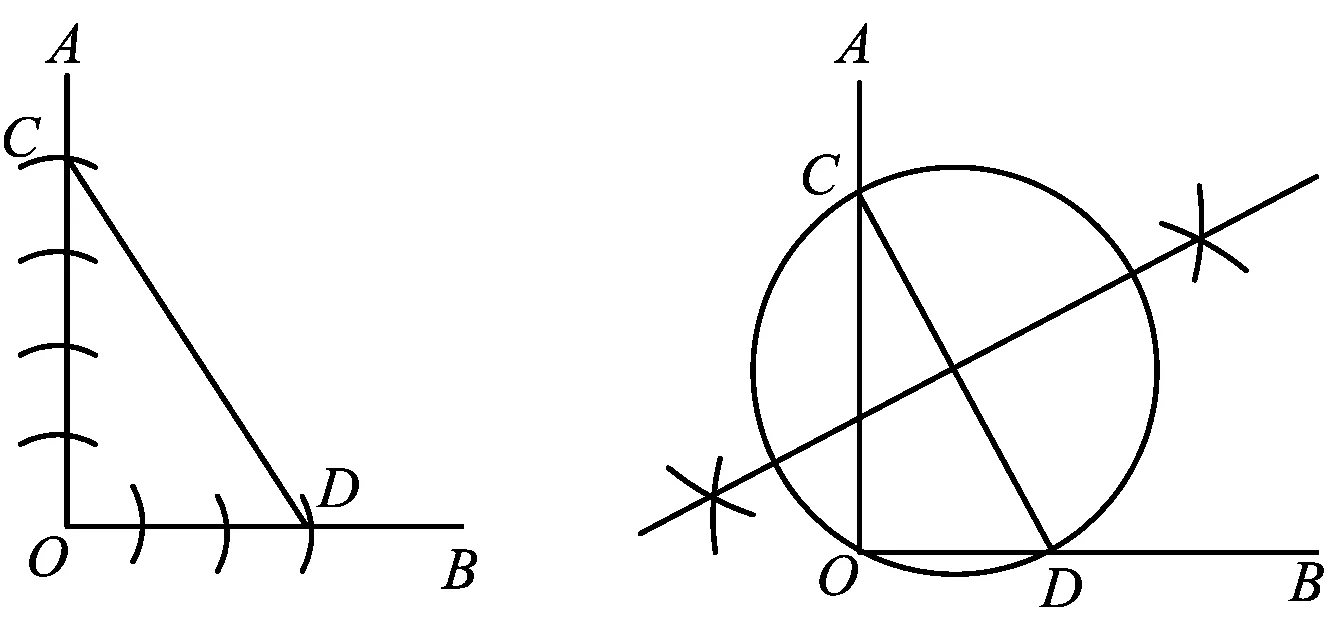
图3　　　图4

方法2如图4，在射线OA,OB上分别取点C，D,以CD为直径画圆.若点O在圆上，则∠AOB=90°．

分析方法1是根据勾股定理作图，方法2是根据直径所对的圆周角为直角作图．

2　特色解读

2.1起点低，通俗易懂

命题的起点是直角，而直角在初中几何中无处不在，这种低起点的命题，让每一个考生都有一种熟悉感．本题同时给出了一种示例(小丽的方法)，让学生可以参照示例展开思维，给学生以思维的启迪．命题者给出示例，无疑是想给学生搭设台阶，让学生拾级而上.示例让本题更通俗易懂，而不是一开始就置学生于死局，让学生觉得“跳一跳可以够得到”，因此本题无疑是一道起点低、人人能读懂的好题．这种命题正切合了《义务教育数学课程标准(2011年版)》(以下简称《课标》)提出的培养目标，要面向全体学生，适应学生的个性发展需要，使得：人人都能获得良好的数学教育，不同的人在数学上得到不同的发展．

2.2立意新，体现公平

“直角在初中几何学习中无处不在”以此命题，这对所有的考生都是公平的.在初中的几何学习中，直角就像空气，存在于几何学习的任何一个角落.对于尺规作图，常规的试题均是给出要求，让学生按要求用尺规作出相应的图形.本题一反常态地设置了一道开放性习题，而开放性试题一般在几何证明题中出现频率比较高，在尺规作图中出现开放性试题，可谓立意新颖．本题区别于以往的试题，不是直接让学生作出直角，而是重在考查学生是否会思考，能否思考得到利用直角来解决的相关途径，这才是本题的核心所在.而这一环节正是解决此题的一个建模过程，在作图题中考查建模思想方法，可谓让人耳目一新．

对于这种题型，可能需要学生在草稿纸上先构思草图，这也考查学生作草图的能力，再依据草图，思考如何依据草图完成尺规作图，以达到本题的预期结果.本题考查的方式亦新颖别致，给出一个角，通过尺规作图来判断此角是直角．也就是说用尺规完成基本作图，在完成作图后还渗透了对几何推理以及数学思想方法的考查，如方法1就是利用勾股定理来构造直角，而勾股定理正是数形结合思想方法的典例．试题把基本作图与相关推理、数学建模、数学思想方法相融合，所呈现的立意令人眼前一亮，更是无形中渗透了数学学科核心素养中的逻辑推理、数学建模能力．

2.3蕴意深，鼓励创新

试题让考生给出两种不同的方法，给学生留下了很大的创新空间.由于每一位考生的思维不一样，每一位考生都用自己擅长的知识来解决此题，因此设置此题，鼓励了学生的创造性.美国科学家贝尔曾说过：“创新有时需要离开常走的大道，潜入森林，你就肯定会发现前所未见的东西.”解题需要创新，这样才能培养学生的创新思维．由于开放性的设计，学生所用的方法涵盖了《课标》中有关尺规作图的大部分内容．正是这种开放性，鼓励了学生自己独立思考，学会思考，这样学生才有创新的空间，才能点燃思维的火花.因为题目要求给出两种不同的方法，学生在给出解答的过程中，势必要构思解决问题的途径及策略，在寻找途径的过程中，就蕴含运用不同的思想方法、不同的建模过程以及对应不同的推理过程，这里所有的不同，均体现了创新，意在鼓励学生的创造性思维．本题除了参考答案的两种方法，还有以下5种不同的方法：

图5　　　图6

方法4如图6，在射线OB上任取一点C，作线段OC的垂直平分线EF，交射线OB于点D；作∠HOB=∠EDB，若射线OH与射线OA重合，则∠AOB=90°．

方法5如图7，以点O为圆心、以任意长为半径画弧交射线OB于点E；再以O为圆心、以任意长为半径画弧交射线OA于点F；作线段EF的垂直平分线MN，交线段EF于点H；联结OH，若OH=FH=EH，则∠AOB=90°．

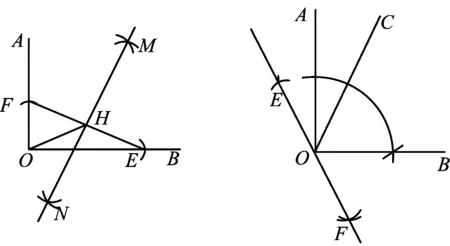
图7　　　图8

方法6如图8，在∠AOB内，任意作一条射线OC；作∠EOA=∠AOC，∠FOB=∠BOC，若点E,O,F在同一直线上，则∠AOB=90°．

图9

方法7如图9，在射线OA上任取一点C，以点C为圆心、以OC的长为半径画圆，若射线OB与⊙C相切于点O，则∠AOB=90°．

还有许多方法，限于篇幅，不再赘述.

3　试题对教学的启示

3.1重深度思考，培养学生思维的深广度

《课标》指出：数学教学活动应激发学生的兴趣，调动学生的积极性，引发学生的数学思考，鼓励学生的创造性思维；要注重培养学生良好的数学学习习惯，让学生掌握恰当的数学学习方法．它指出：能够运用尺规作图完成基本作图；能用基本作图完成部分与三角形、圆有关的作图；了解作图的原理等内容．是的，我们的教学肯定不能只停留在知识和技能上，更应该教会学生学会“数学思考”，让知识变得透彻，让思维得以延续，让数学本质得以挖掘，启发学生学会数学思考[1]．

本题虽是一道作图题，却涵盖了初中阶段的大部分尺规作图，试题的开放性，更是注重学生的思考，符合课标提出的要求．波利亚曾说:“掌握数学就意味着善于解题，不仅善于解一些标准的题，而且善于解一些要求独立思考、思路合理、见解独到和有发明创造的题．”[2]解决本题的关键是通过何种途径作出直角，学生思考的角度可以是：勾股定理；直径所对的圆周角是直角；作垂直平分线；过一点作已知直线的垂线；如果一个三角形一边上的中线等于这边的一半，那么这个三角形是直角三角形；邻补角的两条角平分线构成一个直角；圆的切线垂直于过切点的半径等．只有学生深度思考如何作出直角，才能突破本题.这些方法的出现，正是体现了数学学科核心素养中的数学建模能力，并在建模过程中培养了学生思维的深度和广度．

本题对教学的启示是：教师在教学过程中，不应该就题讲题，而应该在讲解习题时，将习题拓展开来，注重一题多解，把与例题相关的知识汇成知识网．一题多解，更是引发学生思考，培养学生的思维，使知识交互错织．教学中，教师除了课堂上自己引导学生思考题目是否有其他方法外，也要让学生在解题时自己进行思考是否有其他的方法，经常进行这样的训练，久而久之学生就能养成多角度思考问题的习惯，学生的思维也在无形中得到提升．这样学生遇到新问题时，才会启动思维，思考更多的解决问题的途径，甚至当其中一条途径走不通的时候，亦可快速转到另一条途径，而不是钻进死胡同、束手无策．

3.2重经验积累，培养学生的应用意识

《课标》指出：数学活动经验是提高学生数学素养的重要标志．帮助学生积累数学活动经验是数学教学的重要目标，是学生不断经历、体验各种数学活动过程的结果．数学活动经验需要在“做”的过程和“思考”的过程中积淀，是数学学习活动过程中逐步积累的．

积累基本的数学活动经验是《新课标》增加的一项目标，这就要求教师在平时的教学中要注重过程的探究，注重知识的发生、发展过程，学生才能在遇到陌生的题目时，灵活运用已经积累的数学活动经验，将题目剖析到位，从而培养学生的应用意识．本题中的方法5、方法6其实是平时做题中的经验总结，把平时做过的题目中得到的结论灵活运用到新的试题中，这正体现了学生的应用意识．

本道中考题给教学的另一个启示是：教师在平时的教学中，应教会学生如何分析题目，而不是直接告诉题目答案．这种分析题目的过程，寻求解决问题的途径，亦是一种数学活动经验的总结，同时在解题之后，应引导学生及时总结题目所蕴含的结论以及所涉及的思想方法，以便灵活运用到其他的试题中．平时教学中更要注意加强知识的纵横联系，帮助学生构建合理的知识结构与知识系统，提高学生在新问题情境下准确把握核心知识、形成解题决策的能力[3]．这就要求教师在讲解习题的过程中，应多问几个“为什么”，多设几个探究活动，注意知识的“生长点”“延伸点”，每一道题应尽可能地让学生思考不同的方法，为的是将知识置于整个知识体系中，让学生经历知识的发生发展过程，积累数学活动经验，再用积累的数学活动经验解决陌生的题目，从而提高运用已有经验解决新问题的能力，培养应用意识．也就是说，只有当数学活动经验积累丰富时，才能在做新题时，厚积而薄发，学生的应用意识也在无形中得到提高．

总之，本题起点低，立意新，蕴意深，注重学生各方面能力的考查以及平时的数学活动经验的积累，是一道难得的好题.教师在平时的教学中，应注重引发学生进行深度思考，帮助学生积累更多的数学活动经验．

[1]叶晓武．挖掘教材超越教材——由一道学考题引发的教学思考[J]．中学教研(数学)，2016(4):10-13．

[2]波利亚．怎样解题[M]．涂泓，冯承天，译．上海：上海科技教育出版社，2010．

[3]卢明．稳重求变体现创新——2015年浙江数学高考理科数列试题评析[J]．中学教研(数学)，2015(8):21-25．