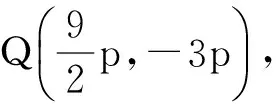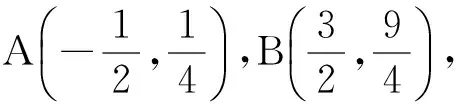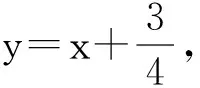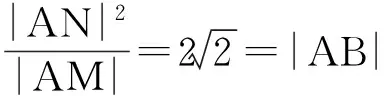算法算理并重 提升数学素养*
——对一道解析几何题的教学思考
● (象山中学,浙江 象山 315700)
1 问题提出
解析几何既是一种重要的数学方法,也是一种重要的数学思想,其本质是利用代数的方法研究图形的几何性质.不久前,笔者听了一节高三解析几何复习的公开课,执教教师以2017年浙江省数学高考试题第21题为例展开教学.笔者通过观察发现,在整个教学活动中,教师教学方式单一,一道例题加几个变式,侧重于几何问题代数化的思路分析,轻视解题过程中运算的分析引导,对其中具体如何运算以及如何优化运算一带而过,导致解析几何题的教学未能很好地落实运算技能,学生解题效率低.

图1

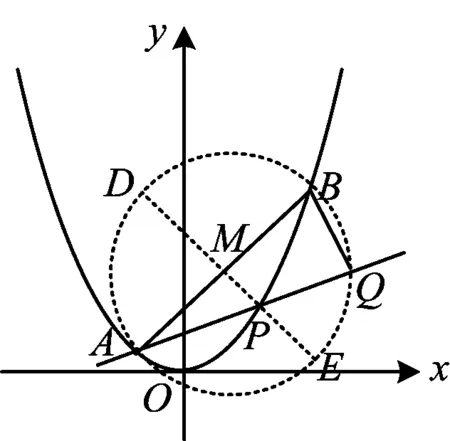
1)求直线AP斜率的取值范围;
2)求|PA|·|PQ|的最大值.
(2017年浙江省数学高考试题第21题)
作为2017年的高考阅卷参与者,笔者深有感触,此题是一道以抛物线为背景的函数值域问题,知识上主要考查直线斜率的概念、直线与圆锥曲线的位置关系,思想上主要考查不等式、函数与方程以及数形结合与转化思想.常见的背景、简单的问题、基本的方法,笔者认为绝大部分考生拿到该考题都会倍感“亲切”,但获得阅卷统计结果后笔者大呼意外,此题全省平均分为4.92(含0分)、5.63(不含0分),可见29.1万考生中近3.6万人得分为0.如此结果,与其说考生临考心理压力大,不如说这是平时教学中教师对解析几何问题只重视“解”与“析”而轻视解题过程的具体运算与算理的揭示,忽视学生核心素养提升的结果.这不得不令人反思,解析几何的解题教学目标应该是什么?
2 聚焦运算,对运算进行“微研究”
数学运算是数学活动的基本形式,也是演绎推理的一种重要形式,是得到数学结果的重要手段.但实际教学中笔者发现,很多学生运算能力不足,一旦运算较为繁杂,信心受挫,学生就会在“思路易知,运算难行”的兴叹中无奈放弃.这是学生畏惧解析几何题的主要原因之一.因此,在解析几何解题教学过程中,教师应引导学生探究运算程序的设计,揭示运算中的数学思维过程,理清思维走向中的每种转化与运算视角,展示运算过程的细节,带领学生分析实施算法的运算长度及合理性,评估其中可能的思维障碍,并及时作出改进与优化方案使学生获得运算求解的基本经验.
解题时的算法设计就是学生在解题时给思维方向定下的基调,就第1)小题而言,思路形成后的算法可以如下设计:
思路1:由点P的坐标,表示出直线AP的方程.
思路2:由直线AP与抛物线有交点,将问题从不同知识视角进行转化.
思路3:计算目标量的范围.
一般而言,问题的转化方向取决于学生对题目条件的理解与认识,方向不同会导致运算上的繁简不同.在教学中,我们需要对其中的运算做进一步的“微研究”:对于思路1和思路2,教师可引导学生在不同转化视角方向下,分析选择直线方程不同的形式对后续运算的影响,让不同层次的学生感受到不同的设法导致的运算长度差异.
分析设成点斜式直接而熟悉,但可能因为在具体解题所采用的转化策略中,字母较多,目标意识不强,在消元、变形时迷失方向;而直线的参数形式虽平时运用少而较陌生,但变量较少,化简方向明确.据此分析,学生将会结合自身实际情况选择合适的运算方式,进而形成基本活动经验.
1)解记P(m,m2),设直线AP的斜率为k,则直线AP的方程为
即
4kx-4y+2k+1=0.
转化1(方程与不等式视角)联立直线AP与抛物线方程,由韦达定理,得
故
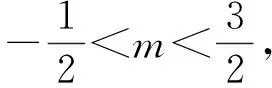
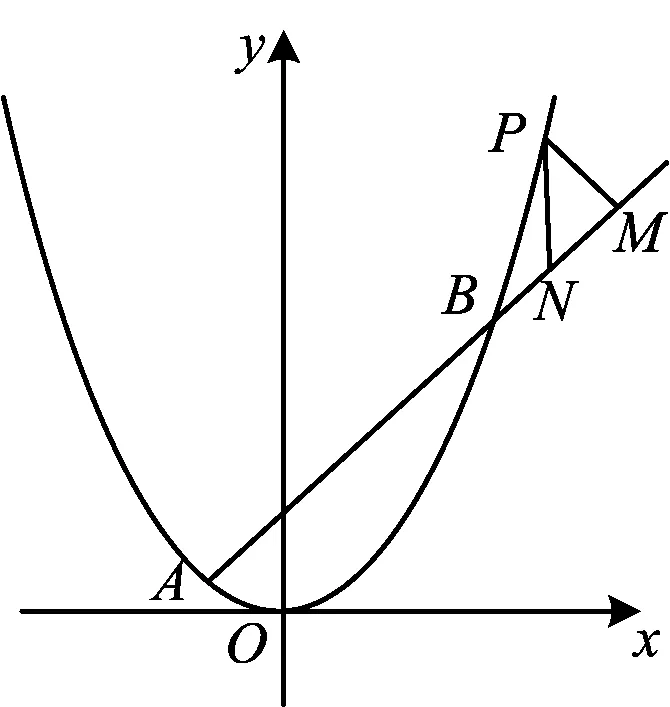
解得-1 即直线AP斜率的取值范围为(-1,1). 转化3(根的分布视角)因为直线AP与抛物线x2=y有交点A,P,由 记函数f(x)=4x2-4kx-2k-1,则 解得-1 即 于是 -1 转化5(直线的参数方程视角)设直线AP的倾斜角为θ,则θ∈[0,π),且AP的参数方程为 点评思路2是学生在课堂学习中提升数学运算素养的重要环节,有必要让学生体会到运算方式的差异对运算速度和准确率的影响.在计算“AP斜率的取值范围”时,其运算方式可以是直接运用斜率计算公式,也可转化为研究其满足的数学关系,两种方式对解题的运算长度影响迥异,对学生思维的要求也不同,前者是单向线性的思维体现,后者则是多向整体思维的交互. 通过问题对解题的算法设计、运算节点进行切片式的“微研究”,解析几何例题的教学方式不是单一的、枯燥的讲题与被动机械的演练,而是一个使学生的思维由浅入深、从粗到细慢慢展开的生动活泼、充满探索与思辨的活动过程.在这个过程中,学生既有对自己已有运算经验的调整与反思,也有对他人思维的借鉴与模仿,还有对代数式观察、运算方向监控、运算长度预估等多重的思维训练.在这样的过程中,学生的思维品质和数学运算素养都将得到相应的提升. 数学运算是运算技能与逻辑思维等的有机结合,是数学素养中最基本的技能和最基本的素质.任何运算都离不开算理的支撑,算理为分析运算条件、理解运算对象提供正确的思维方式,保证运算方向探究的合理性和运算方法选择的正确性.在教学中,教师重视具体算法的形成和例习题的数量,贪多求快,而不愿放慢脚步引导学生提炼揭示算理,认为这是高中学生本应具备的“基本素质”.欲速则不达,学生“屡算屡错”不仅是“算法”不好,运算技能不过关,更主要的是算理不明.对相应的例题仔细剖析算理,有助于学生寻找合理简洁的运算途径去解决问题. 第2)小题的算法常规设计思路如下: 思路1:由直线AP与BQ的关系,得到BQ的方程. 思路2:求得点Q的坐标,进而确定|AP|,|PQ|的表示式. 思路3:计算|PA|·|PQ|的最大值. 实现以上算法可得到以下具体解题过程: 2)解法1因为BQ⊥AP,故直线BQ的方程为 联立直线AP,BQ的方程,解得 又点P(m,m2)满足方程 则 因此 |PA|·|PQ|=-(k-1)(k+1)3, 这种根据题目循“叙”渐进的算法易想难算,需要教师引导学生深入剖析算法背后隐性的“算理”.优化解题思维,追求算法的多样化与灵活性,实现多想少算或巧算,防止“一算到底”,才有助于学生学会独立地探索问题更优良的算法,为解决问题发现合理简洁的运算途径. 回顾以上运算过程,可以发现“消元”是显性的算理,而“转化”思想则是隐藏其中的基本算理,但如何转化、向什么方向转化则是需要细加剖析的.反思|PQ|的表示,点Q的坐标是不是必须明确求出?算理与具体的数学知识紧密相联,教师梳理解析几何的代数运算性特点,为学生解法的“再创造”提供更多的素材:解释平面几何图形的基本知识有角与距离,涉及的公式有斜率、两点间的距离(弦长)、点线距离、勾股定理与正余弦定理以及向量工具等.这些知识应用的关键在于:思考如何通过分析图形的几何特点,转化到可利用对应的基本公式运算.算理的“细剖析”启发学生思考“为什么这样转化运算”,促使学生根据自身的知识理解情况选择更适合自己的“算法”进行运算,使学生在活动中优化解题策略,积累方法和经验. 又BQ⊥AP,则点B到直线AP的距离 由勾股定理,得 因为k∈(-1,1),所以由均值不等式,得 |PA|·|PQ|=|(k+1)3(k-1)|= 图2 解法3如图2,联结BP.由BQ⊥AP,得 |PQ|=|PB|cos∠BPQ=-|PB|cos∠BPA. 在△ABP中, 由余弦定理,得 |PA|·|PQ|=-|PA|·|PB|cos∠BPA= 解法4由点A,P,Q共线,得 |PA|=-t1,|PQ|=t2, f′(m)=-4m3+3m+1= -(m-1)(2m+1)2≥0, 图3 |PA|·|PQ|=|PD|·|PE|= (|MD|+|MP|)(|ME|-|MP|)= 故当|MP|最小,即以M为圆心、以MP为半径的圆与抛物线x2=y相切时,|PA|·|PQ|最大.此时,以MP为半径的圆与抛物线x2=y在点P(m,m2)处有公切线,切线斜率为 k=y′=2m, 整理得 4m3-3m-1=0, 即 (m-1)(2m+1)2=0. 运算不能离开具体的数学知识而孤立进行,也离不开记忆观察、联想理解.通过“BQ⊥AP”这一关键信息进行代数意义的研究或几何位置关系上的揭示,选择变量之一进行消元,选择利用多种知识从不同角度表示出目标式|PA|·|PQ|,再结合基本不等式或由|PA|·|PQ|的抽象形式表示转化为几何直观理解,以形助数将目标式中的变量实现整体消去,优化运算过程而求得结果.显然,算理的提炼帮助学生透彻理解算理,消除学生执行算法时的盲目,避免复杂的运算,让学生在“以原理指导过程”的剖析中,感悟获得进行类似操作的思维范式,对学生形成计算技能、提高运算信心大有帮助. 高三数学复习教学应成为学生期待的课堂,教师应尽量通过典型例题使学生有新收获,能发现典型例题背后的新鲜事,避免使之成为“一本资料、一块黑板、一支粉笔”加上“一个演员”的独幕剧.这需要师生共同通过对数学知识深层次的思考,揭示蕴涵其中的数学思想方法,挖掘问题背景,激发学生研究问题的意识和能力;提升例题的附加值,使其教学价值向深层延伸,发挥应有的教学功能,使学生学会用数学的眼光主动探求知识,学会数学抽象,积累从具体问题到抽象的活动经验. 再次引导学生回顾反思上面的解题过程,注意到当|MP|最小时,直线MP与点P处的切线互相垂直,即直线MP是抛物线在点P处的法线,不难收获两个简单的性质: 性质1若抛物线外一点M与抛物线上点P的距离|PM|最小,则抛物线在点P处的法线经过点M. 继续引导学生通过观察猜想、运算归纳、推理论证等一系列的思维活动,寻找问题背景的奇异处,可以发现直线AB是抛物线在点A处的法线,抛物线的法线有什么特别性质吗?沿命题者的思维轨迹尽可能延伸下去,就有可能发现抛物线法线的一个更美丽的结果. 图4 进一步,可以将结论1推广到一般情况:若点A,B为抛物线y2=2px(其中p≠0)上的两个点,且直线AB为抛物线点A处的法线,则对抛物线上任意异于点A,B的动点P,作PM⊥AB,PN⊥x轴分别交直线AB于点M,N,有|AN|2=|AM|·|AB|(限于篇幅,不再赘述其证明). 总之,解析几何是高考的热点与重点内容之一,也是学生所面临的解题难点.思路诚可贵,运算价更高,运算的作用不仅仅是求出结果,还隐藏着严谨的代数论证.学生对解析几何问题的理解,直接影响他们解决问题时算理的选择和运算策略的制定.在复习过程中,教师既要突出解析几何用代数语言描述几何要素及其关系、将几何问题转化为代数问题的思想,更要让学生体会到如何运算,体验用发现的眼光看到“门里的诗画盆栽”,欣赏到“门外的雄川峻岭”,促进学生逻辑推理、运算求解能力的提高,体会数学学习的乐趣,从而提升学生的数学素养.
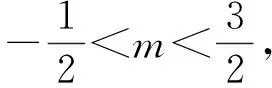
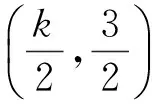

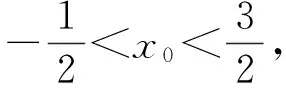
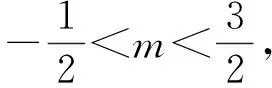
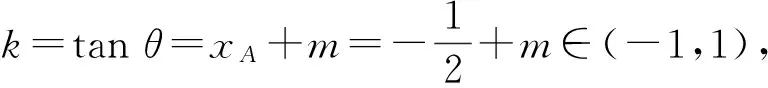
3 理解算理,对算理进行“细剖析”
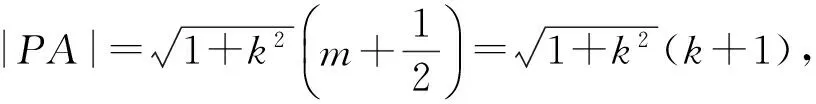

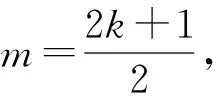

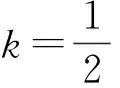
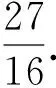
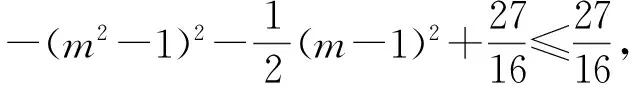


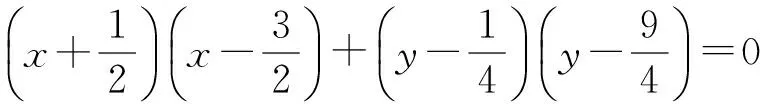

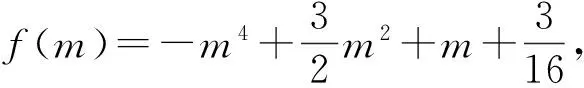


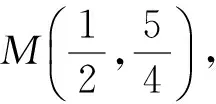

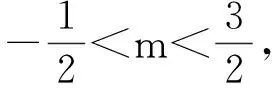
4 揭示背景,对问题进行“深思考”