紧俏供应链网络的库存优化策略

高德宝，于　辉

在供应链管理环境下，每个环节的库存量和订货量是矛盾的两个方面.许多学者从不同的角度对这一课题做出了积极的研究.文献［1-2］分别从回购契约和商品有价格折扣两方面研究了两级供应链的库存问题；文献［3-5］探索了不确定供需条件下的商品订购问题；若有一定的约束条件，文献［6-9］对其进行了一定程度的探索；而文献［10-11］对特殊商品的采购与库存问题给出了解决方案.但是，紧俏商品供应网络的库存与订货问题鲜有人研究.

随着我国物流体系的不断充实与完善，商品生产供应商与终端客户之间的流通环节及物流费用越来越少，流通速度越来越快.特别是紧俏商品，因其需求旺盛与供不应求的特性促使其流通环节更少，流通速度更快.一般的情况下，紧俏商品的流通环节基本上是“生产供应商——批发商——销售商——终端客户”.源于利益的驱动，紧俏商品的批发商之间、销售商之间几乎没有商品流动，而批发商与销售商之间的商品流量和流动方向是单一且清晰简单的.若非紧俏商品，为促进产品的销售速度，供应链网络内部会发生不规则的商品流向和混乱的商品流量问题.

本文研究的紧俏供应链网络假设仅有一个生产供应商，n个批发商，每个批发商对应若干个销售商；批发商与批发商之间、销售商与销售商之间不会发生货物流转的情形；每个销售商仅从其对应的上级批发商进货.这个紧俏供应链网络如图1所示.

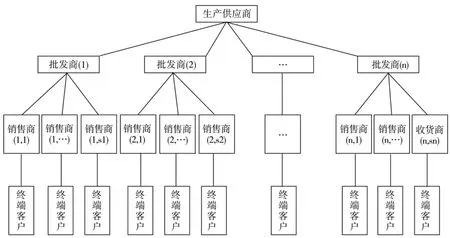
图1　紧俏供应链网络

设批发商i(i=1,2,…,n)给si个销售商补货.驱动整个供应链网络利润的源动力是各销售商的单位时间需求率，设销售商 j(j=1,2,…,si)单位时间的平均需求率为sdij；由于所有批发商均从同一个生产供应商处进货，从而他们的进货价是相同的，设其单位进货价为wc.但是，不同地区的经济发展水平不一致，同一商品在不同的批发商处或销售商处的每次订货费和单位时间单位货物的库存费、售价和缺货费可能不同.设销售商 (i,j)(j=1,2,…,si)从批发商 i(i=1,2,…,n)处每次的订货量、订货费分别为sqij,skij，单位商品单位时间的库存费、缺货成本，单位商品的进价和售价初始库存分别为shij,sbij,scij,spij；批发商i每次的订货费，单位商品单位时间的库存费、缺货成本、单位商品的售价和每次的订货量分别为wki,whi,wbi,wpi,wqi.

批发商要向多个下游销售商供货，因为商品的紧俏性或供不应求性，所以下游销售商发来的订单请求未必能得到全部满足，记下游销售商实际收货量占其需求量的百分比的值为到货率.目前该商品较为紧俏，末端销售商需求旺盛，到货率也仅有 A（＜1）.

1　销售商的库存策略

虽然销售商可以提前订货且可以认为是瞬时到货的，但是因为商品到货率A小于1的原因（根本原因是供不应求），总是会发生缺货的情形.因此，本文销售商的库存变化过程如图2所示，其中S,s,Q分别为一个销售周期内库存的最大水平、缺货的最大水平和每次的到货量.因为每次的到货率为A，所以可以认为目前的商品生产能力满足需求的比例为A，而缺货率为1-A.因此 s=(1-A)sqij,S=A·sqij-s=(2A-1)sqij.

图2　销售商的库存变化

在图2中，假设销售商(i,j)(i=1,2,…,n,j=1,2,…,si)的某个销售周期为时间段[T0,T1].在这个周期内，该销售商所获得的平均利润函数为

解方程

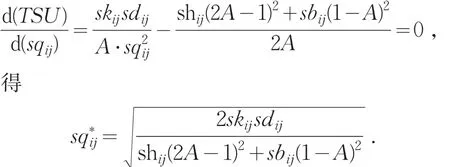
这个销售周期的时间长度为

销售商(i,j)库存量非零的时间长度为

销售商(i,j)缺货的时间长度为

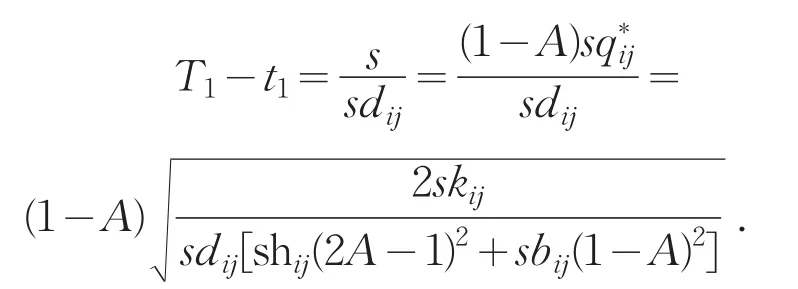
销售商(i,j)一个销售周期内的平均库存量

为

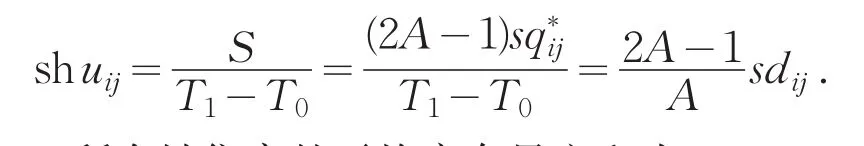
所有销售商的平均库存量之和为

销售商(i,j)一个销售周期内的平均缺货量为

所有销售商的平均缺货量之和为

当所有销售商的平均库存量之和为shu，且平均缺货量为sku时，所有销售商在这个销售周期内的平均利润之和最大.当供货率A增加时，销售周期、库存时间会增加，而缺货时间、平均库存量、平均缺货量会减少.

2　批发商的库存策略

生产供应商受生产能力的限制，对每个批发商的实际需求量不能全部满足，但会以固定的速率对其进行补货.由于流通环节少，又多数是远距离运输，所以可以认为批发商的补货是瞬时到货的.而批发商会根据自已的实际库存情形按一定的比率（即到货率）对每个销售商进行补货，从而不会发生缺货的情形.批发商i(i=1,2,…,n)的出货量与所有对应销售商补货量之和的比值为 A(＜1).即批发商i的实际出货率为wdi=.批发商i单位时间内的利润函数为

解方程

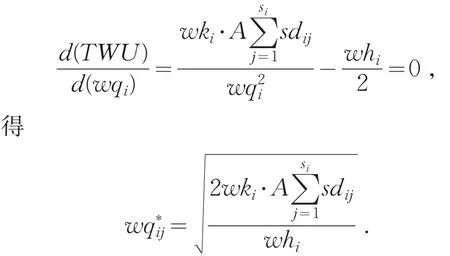
批发商i的最大利润与订货周期分别为

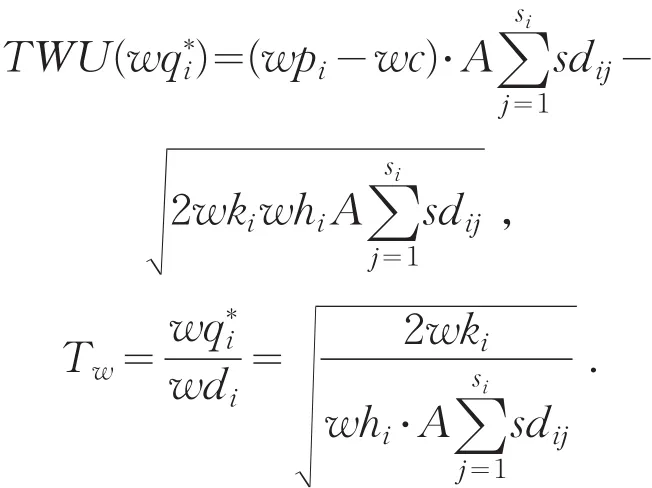
从上述表达式可以看出，订货周期会随着A的增大而减少.反之，则相反.若需考虑全体批发商的最大利益，只需对每个批发商的最大利润求和即可.

3　生产能力提高的库存优化策略

随着生产技术与生产工艺的提高，生产能力也必会随之提高，从而导致供应能力提高，销售商的到货率也会增加.此时，销售商的利益不仅与订货量有关，还与到货率有关，则销售商(i,j)的平均利益函数为

解方程组

得

因此，销售商(i,j)的平均利益函数最大值为

此时销售商(i,j)的销售周期的时间长度为

从A*的表达式可知道A*＜1.即对于销售商而言，当到货率为1时，他的利润反而不是最大值；相应地，需求量得到全部满足时，也不会获得最大利润.同样，当生产能力提高到一定程度时，为保证销售商获得最大利润，批发商为销售商提供的补货量也不要全部满足.而对于生产供应商而言，生产能力提高到一定程度，其供货能力达到A*即可，否则会出现通货膨胀的情形.

在到货率为A*，订货量为sq*ij的条件下，我们会得到如下一些主要结论.

销售商(i,j)库存量非零的时间长度为

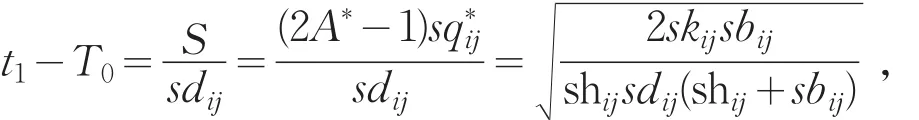
销售商(i,j)缺货的时间长度为

销售商(i,j)一个销售周期内的平均库存量为

所有销售商的平均库存量之和为

销售商(i,j)一个销售周期内的平均缺货量为

所有销售商的平均缺货量之和为

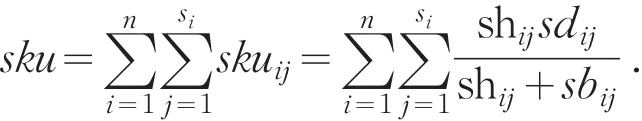
4　结论

对于异地异价的情形，本文探索了紧俏供应网络中批发商与销售商为获得最大利润而需要的订货量与销售周期.在生产力提高的条件下，同样为了获得最大的利润，研究了最佳的供货率、订货量和销售周期.对于统一价格的情形，文中并未作讨论，因为只需将相应结论中的量进行替换即可.本文的结论完全可以推广应用到类似连锁超市中某一类有唯一生产供应商的商品.

参考文献：

［1］马小勇，陈良华.考虑零售商库存转运的两级供应链回购契约协调机制研究［J］.统计与决策，2017（2）：43-46.

［2］祝小艳.基于价格折扣的两级供应链库存控制模型研究［D］.淮南：安徽理工大学，2009.

［3］陈群，韩景倜.随机订货成本扰动下零售商鲁棒与机会约束订货策略［J］.统计与决策，2017（1）：43-46.

［4］李丽.模糊随机供需变量的VMI的订货量模型［J］.统计与决策，2011（7）：58-61.

［5］赵伟伟.到货时间不确定的多商品订购批量优化模型及算法研究［D］.沈阳：东北大学，2014.

［6］张桂涛，孙浩，胡劲松.考虑库存能力约束的多期闭环供应链网络均衡［J］.管理工程学报，2017，31（1）：176-184.

［7］初叶萍，张曙红.闭环供应链混合切换库存控制模型研究［J］.计算机应用研究，2017，34（6）：1-6.

［8］杨光.连锁超市库存管理系统仿真应用研究［D］.重庆：重庆交通大学，2012.

［9］贾涛，刘玉伟，徐渝，等.库存量影响需求的反向条件延期付款订货策略［J］.运筹与管理，2016，25（4）：157-167.

［10］张俊尧.供应链网络下白沙物流库存控制优化［D］.济南：山东大学，2012.

［11］宋毅斐，鹿岩，孙世光.基于库存模型法的药品采购与库存控制策略［J］.中国药房，2016，27（1）：70-73.