一种空中动目标定位跟踪及航速航向估计方法

孟金芳，付 喜

(中国电子科技集团公司第三十六研究所，浙江嘉兴 314033)

0 引 言

在任何时期，对动目标的态势感知和预判能力都有着迫切的需求，而现有设备对动目标(尤其是空中动目标)的监视能力还十分有限。为了实现对动目标的态势感知和预判能力，就必须利用一切可以利用的手段实现对这些威胁目标实施侦察，对其“一举一动”进行有效的掌控，包括情报信息、位置信息以及速度信息、航向信息等。

利用高轨卫星对空中动目标进行定位，能够在较大的范围内(覆盖5000 km×5000 km区域)的目标进行侦察、定位和跟踪。星载定位体制主要有单星测向交叉定位[1]、三星时差定位[2-3]、双星时频差定位[5-6]等类型。三星时差定位体制具有适用范围广，实现简单，定位精确度高等优点，受到世界各国的普遍重视。现在的三星时差定位针对固定目标进行定位或者定位精度分析[2-4]，不能适应空中快速目标的定位与跟踪，不能在对目标定位的同时估计出目标的航向航速信息。本文以高轨卫星星载平台测得的空中运动目标时差信息为基础，应用EKF和UKF滤波方法对目标的位置和航速航向进行跟踪，并给出仿真结果。

1 三星时差定位跟踪原理

三星时差定位[4]源信号到达主星和其中一个辅星组成的侦察基线之间存在着时间差，由这个时间差可以绘制一个所有可能的辐射源位置的双曲面，如果主星和另外一个辅星组成另外一条侦察基线，则可以得到另外一个双曲面，两个双曲面的交点得到所有可能的辐射源位置的曲线。该曲线与地面模型的交点即为辐射源的位置。

设时差定位系统由一个主站和N个辅站组成，本文采用地心坐标系，各测量站的位置坐标为(xi,yi,zi)，i=0,1,2,其中i=0表示主站，i=1,2表示辅站，目标辐射源的位置坐标为(x,y,z)，则辐射源和各个测量站之间的距离为：

(1)

=Ki-2xix-2yiy-2ziz+x2+y2+z2

(2)

令τi0表示辐射源到达辅站i和主站0之间的TDOA测量值，则

(3)

其中c为电波传播速度。

该方程与地球表面作为定位面的方程进行联立，得到如下式所示的时差定位方程组：

(4)

其中a为目标相对于地心形成的球面半径，r为地球半径，h为目标相对于地面高度。

对该方程进行求解可以得到目标的位置信息，但是不能求出目标的航速和航向信息，其中航速信息可以通过滤波的方法求出。

2 滤波[7]过程

目标定位与跟踪问题的非线性源于状态方程和观测方程中函数的非线性以及相关噪声过程的非高斯性，所以卡尔曼滤波成立的前提条件不满足，而要采用偏微分方程来描述滤波问题，目前在实际处理跟踪滤波问题中用得最多的仍然是基于EKF技术的方法。

在地心坐标系下，动目标采用离散匀加速运动模型[8]，其状态变量为X(i)=(x(i),y(i),z(i),vx(i),vy(i),vz(i),ax(i),ay(i),az(i))T，其中(x(i),y(i),z(i))T为目标的位置向量，(vx(i),vy(i),vz(i))T为目标的速度向量，(ax(i),ay(i),az(i))T为目标的加速度向量。系统的状态方程可以描述为：

X(i+1)=f(X(i),w(i))=FX(i)+Γw(i)

(5)

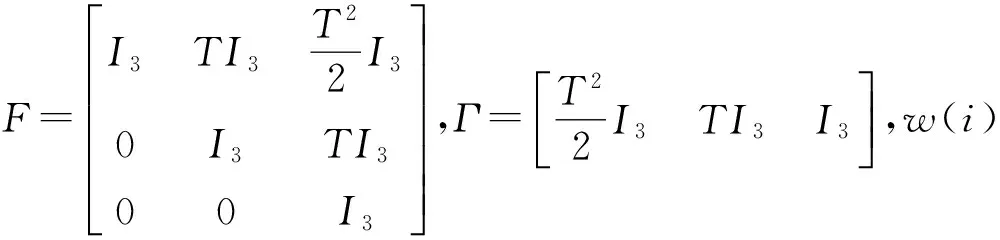
(6)

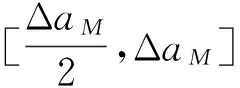
由式(4)可以得到系统的观测方程为：

(7)

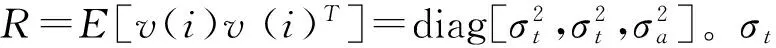
以式(5)为状态方程、式(7)为观测方程组成一个EKF滤波模型，对动目标进行跟踪，并求取目标的航速信息。滤波过程如下：

预测方程为：

(8)

预测协方差为：

P(i,i-1)=FP(i-1)FT+Q

(9)

测量方程的雅克比矩阵为：

(10)

卡尔曼增益为：

K(i)=P(i,i-1)H(i)T

[H(i)P(i,i-1)H(i)T+R]-1

(11)

滤波方程为：

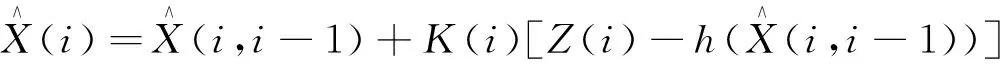
(12)

滤波协方差为：

P(i)=[I-K(i)*H(i)]*P(i,i-1)*

[I-K(i)*H(i)]T+K(i)*R*K(i)T

(13)

应用EKF滤波得到目标的航迹和航速信息，根据航速计算实时航向信息，具体如下所示：

航向角为：

(14)

俯仰角为：

(15)

速和航向信息，其中航速信息可以通过滤波的方法求出。

3 UKF滤波[9]过程

在实际处理目标定位于跟踪问题中用得最多的是基于EKF滤波的方法，但是容易出现线性化误差大和协方差容易出现病态等缺点，UKF(Unscented Kalman Filter)算法是对EKF的改进，利用UT变换的方法选取Sigma样点，更好的近似随机变量非线性变化后的统计值。与传统的EKF算法相比，UKF在解决非线性问题时通常能获取更高的精度，并且对噪声具有很好的适应性。

(16)

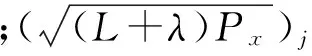
将这些样点通过非线性变换，即：

y=g(χj),j=0,1,…,2L

(17)

计算权值：

(18)

其中调节参数β可以提高方差的精度。

则变量X经过非线性变换后得到y=g(χ)的均值和方差为：

(19)

非线性系统的状态方程和观测方程分别如式(5)和式(7)所示。

(1)滤波初始化：

(20)

(2)计算样点：

根据式(16)样点的选取策略，对于时刻i-1，得到采样点{χj(i-1)}，j=1,…,L。

(21)

(3)状态变换预测：

χ(i|i-1)=f(χ(i-1),w(i-1))

(22)

(23)

(24)

(4)测量变换预测：

Z(i|i-1)=h(χ(i-1),v(i-1))

(25)

(26)

(27)

(5)状态、测量预测互协方差：

(28)

(6)权增益及状态更新：

(29)

(30)

(31)

应用UKF滤波得到目标的航迹和航速信息，航向信息的计算如式(14)和(15)所示。

4 仿真分析

为了验证EKF和UKF滤波在星载对空中动目标航迹定位及航速航向估计上的应用效果，在MATLAB平台上编写软件进行仿真分析。三颗卫星轨道高度为36000 km，呈三角形分布，最大星间距为2000 km，目标在距离地球表面10 km高度做匀速运动。设卫星自定位误差均方差为100 m，时差估计误差均方差为200 ns，假设地球半径测量误差为10 km(该误差实际代表了目标相对地球表面的高度值，具体见式(7)的描述)。根据式(8)～(13)得到EKF滤波过程，根据式(20)～(31)得到UKF滤波过程，目标滤波初值由式(4)通过解析法获取(求取初始值时假设目标高度为0 m)，滤波结果如图1～图3所示。

图1 定位跟踪效果图

图2 滤波后的定位误差曲线图

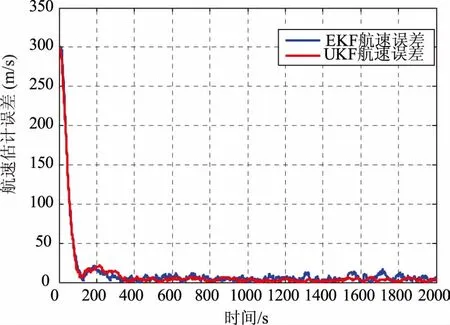
图3 滤波后的航速误差曲线图

从图1～图3可以看出，本文所用的方法能够跟踪动目标运动轨迹，并同时跟踪目标的速度值。EKF在200 s后定位误差能达到公里级别，稳定后均方根误差为8.1 km，200 s后航速估计误差在20 m/s 以内，均方根误差为6.3 m/s。UKF在200 s后定位误差能达到1 km左右，稳定后均方根误差为0.768 km，200 s后航速估计误差在20 m/s以内，均方根误差为5.3 m/s。

EKF对目标的定位误差在8 km左右，这是因为EKF不能很好的估计目标的高度值，UKF比EKF更善于解决非线性跟踪问题，仿真结果证明UKF能够在观测方程的约束下很好的估计目标的高度信息，也能得到更好的定位结果和航速估计结果，可用于长时间对空中动目标进行定位跟踪的场合。

图4 航向角估计误差曲线图

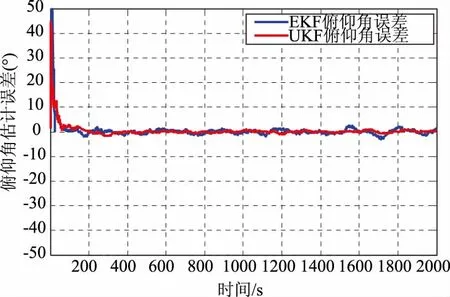
图5 俯仰角估计误差曲线图

从图4～图5可以看出，本文所用的方法能够估计目标的航向信息，包括航向角和俯仰角。EKF滤波稳定后航向角估计误差的均方根误差为0.52°，俯仰角估计误差的均方根误差为0.84°。UKF滤波稳定后航向角估计误差的均方根误差为0.2°，俯仰角估计误差的均方根误差为0.74°。EKF和UKF滤波方法都能够很好的估计出目标的航向信息，相比而言，UKF的航向信息估计的更加精确，适合用于长时间对空中动目标进行航向估计的场合。

5 结 语

本文提出了一种基于滤波(包括EKF和UKF)的高轨卫星星载平台定位跟踪方法，能够对空中动目标进行定位跟踪，同时估计出目标的航速航向信息，仿真结果表明UKF的定位跟踪和航速航向估计能达到很高的精度，使得高轨卫星对空中动目标定位精度达到1 km以内，提高了高轨卫星对空中动目标的态势感知和预判能力。这对于高轨卫星平台下对空中动目标定位跟踪及航向航速估计的工程化实现具有一定的参考价值。

[1] 田明辉，方青，钮俊清等. 星载平台地面目标测向定位仿真研究[J].雷达科学与技术，2012,10(3):262-271.

[2] 曾芳玲，曾辉，杨景曙. 基于WGS-84地球模型的三站时差定位算法[J]. 数据采集与处理，2011, 26(2):214-218.

[3] 李文华. 三星构型设计与时差定位精度研究[J], 宇航学报，2010, 31(3):701-706.

[4] 常新亚，张立华，陶成华等. 三星时差定位系统的目标定位精度分析[J]. 航天器工程，2007, 16(4):121-126.

[5] 张政超，袁翔宇，陆静等. 双星(站)时差频差无源定位误差分析[J]. 中国电子科学研究院学报，2016(1):107-110.

[6] 李瑞玲，基于WGS-84的双星时差/频差定位算法及误差分析[J]. 电子科技，2014，27(2)：53-57.

[7] 孙仲康,郭福成,冯道旺等. 单站无源定位跟踪技术[M]. 北京: 国防工业出版社, 2008，187-188.

[8] 孙仲康,郭福成,冯道旺等. 单站无源定位跟踪技术[M]. 北京: 国防工业出版社, 2008，314-315.

[9] 孙仲康,郭福成,冯道旺等. 单站无源定位跟踪技术[M]. 北京: 国防工业出版社, 2008，188-192.