FIR数字滤波器的设计与研究
王 辉
(海装重庆局,重庆 400030)
0 引言
有限冲击响应(FIR)数字滤波器具有严格的线性相位和任意幅度的特性,并且其单位抽样响应是有限长序列,滤波器极其稳定,因此广泛应用于图像处理及数据传输中。而FPGA具有灵活的可编程逻辑,并且突破了并行处理与流水级数的限制,具有速度快、功耗低、可靠性高和可移植性高等特点。利用IP Core设计FIR滤波器,设计周期短,占用逻辑资源少,运算速度有大幅提高[1],故使用IP Core已逐渐成为数字信号处理的一种方式。本文采用数字仿真方式验证了系统的正确性和有效性。
1 系统总体设计
整个系统由A/D采样电路、FIR滤波器以及D/A转换电路组成。为便于分析系统性能,对一特定的带阻网络进行了测量。A/D转换电路用于采集经过带阻网络衰减后的信号,FIR滤波器对采集到的数据进行滤波,最后通过D/A转换电路输出处理后的波形。系统框图如图1所示。

图1 系统框图
在本设计中,对带阻网络的幅频特性进行测量,得出所需FIR滤波器的频率响应。根据FIR滤波器的频率响应特性,利用Matlab计算出滤波器的系数。并可通过Matlab仿真,验证所设计的系统是否符合要求。最后将验证过的数据导入IP核,即通过FPGA硬件实现所需要产生的滤波器。
2 FIR滤波器的设计
2.1 Matlab函数的设计
Matlab中提供的函数fir2是基于频率取样的FIR滤波器设计方法,其滤波器的频率特性由频率向量f和幅值向量a决定[2]。其基本的调用形式为:

式中,返回的行向量b是一个包含n+1个n阶FIR数字滤波器的系数,此FIR滤波器的频率特性是由f和a决定的。因此,只需要知道幅值与频率的关系,就可计算出任意FIR滤波器的系数。
在本设计中,是通过已知的带阻滤波器的幅频特性来设计一个FIR带通滤波器,要实现数字幅频均衡,则需要满足

式中,H1(jω)为带阻网络的幅频响应,H2(jω)为FIR带通网络的幅频响应[3]。式(2)表明,带通滤波器的幅度值实际上可认为是带阻网络的幅度值的倒数。由带阻网络的幅频特性,便可推算出需要产生的FIR带通滤波器的性能指标。
经实际测量,带阻网络的中心频率f0为3.7 kHz,其通频带BW=f2-f1=3 950 Hz-3 510 Hz=440 Hz.根据带阻网络的幅值取倒得到的FIR带通滤波器的幅频特性曲线如图2所示。

图2 FIR滤波器频率特性曲线
2.2 阶数分析
调用函数fir2()算出300阶时FIR带通滤波器的系数[4],并由用可视化工具fvtool生成的幅频特性曲线如图3所示。

图3300 阶系数的频率特性图
比较图2和图3可以知道,处理后波形的幅频特性图与需要产生的幅频特性图大致相似,但图3的衰减特性还不是很符合要求。将阶数设置为2000时,其频率特性图如图4所示。

图42000 阶系数的幅频特性图
3 系统测试
3.1 不同阶数的比较
保持采样数据的个数不变,只改变FIR带通滤波器的阶数,实际测试的数据如表1所示。

表1 实际幅频特性与阶数的关系
由表1可知,设置的滤波器阶数越高,其通频带越小,衰减特性也越陡峭,也越接近需要设计的FIR带通滤波器。
3.2 资源利用率
而FPGA资源利用率与FIR滤波器阶数近似成正比的关系,因此无限地提高滤波器的阶数的同时,也会大大增加系统的资源损耗[5]。经实际测量,资源利用率与阶数的关系如表2所示。

表2 资源利用率与阶数的关系
3.3 2000阶带通滤波器的实现
2000阶的FIR带通滤波器实际输出幅频特性曲线如图5所示。
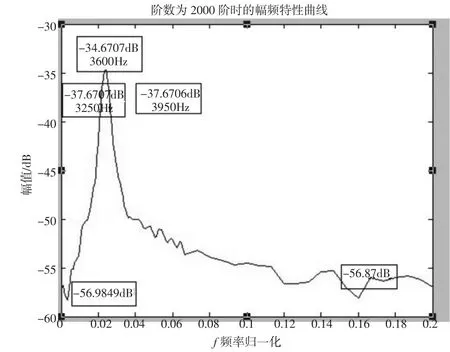
图52000 阶实际输出幅频特性曲线
由图5可知,滤波器阶数为2000阶时的衰减特性可以满足幅频均衡的要求。
4 总结
本设计基于FPGA的IP Core实现了FIR数字带通滤波器,并对如何保证滤波器性能的前提下有效地利用FPGA资源做出了分析。测试结果表明,滤波器阶数设置合理,系统资源分配合理,保证了系统的正确性和有效性。
参考文献:
[1]潘 松,黄继业.EDA技术与VHDL[M].2版.北京:清华大学出版社,2007:14-16.
[2]求是科技.MATLAB7.0从入门到精通[M].北京:人民邮电出版社,2006:62-68.
[3]程佩青.数字信号处理教程[M].3版.北京:清华大学出版社,2009:40-45.
[4]Uwe Meyer-Baese.数字信号处理的FPGA实现[M].刘 凌,胡永生,译,北京:清华大学出版社,2003:73-78.
[5]郝小江,缪志农,张小平.基于FPGA的FIR滤波器设计与实现[J].仪表技术,2010(1):25-26.

