基于模型预测控制的履带式无人平台轨迹跟踪控制算法研究∗

杨福威 孟 红 朱 强

1 引言

精确而稳定的轨迹跟踪控制是实现无人车辆智能化和实用化的关键。国内外学者在轨迹跟踪控制方面做了许多研究，提出了PID控制算法、纯跟踪控制算法、模糊自适应控制算法、模型预测控制算法等。但车辆高速运动时轨迹跟踪的复杂性和路面条件的波动性等问题导致轨迹跟踪控制一直是目前的技术难点［1～7］。

上述控制方法大多需要建立精确的数学模型，但车辆是一个复杂的非线性系统，在工程应用中往往需要对模型进行简化，而高精度的控制方法还需要考虑各种不确定因素，这些都会导致控制问题的复杂化。

模型预测控制算法是一类滚动求解带约束优化问题的控制方法。模型预测控制具有预测模型、滚动优化和反馈校正的优点，能够克服复杂环境下的跟踪误差和随机扰动，能够及时弥补模型失配以及外界干扰引起的不确定性，适用于数学模型建立不精确且存在约束条件的系统［8～15］。

本文首先建立了履带车辆在打滑条件下的运动学模型和基于地面力学和剪切变形理论的非线性动力学模型。基于两种模型设计线性时变预测控制器，将无人车辆的轨迹跟踪问题转化为标准的二次规划问题。最后在MATLAB/Simulink中建立车辆动力学模型和预测控制器，验证了控制算法的准确性和鲁棒性。

2 运动学模型

首先建立全局坐标系XOY和固定在车辆上的局部坐标系xoy，局部坐标系原点为无人车辆质心位置。将无人车辆运动模型简化为二维模型，选取左、右两侧转速为控制量。运动学模型如图1所示。

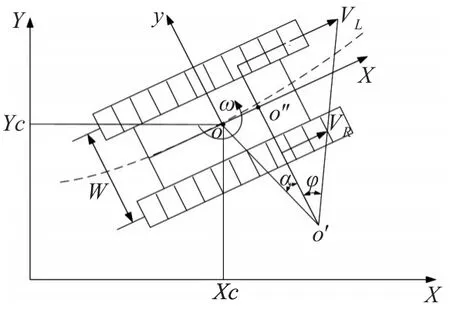
图1 履带车辆运动学模型

无人车辆质心运动方程为

由式（1）可知，通过控制两侧主动轮的转速，即可得到无人车辆相应的速度和转角。在考虑打滑率和打滑角的情况下，运动学模型为

其中iL、iR分别为两侧履带的打滑率，α为车辆速度方向与纵向方向的夹角，计算公式为

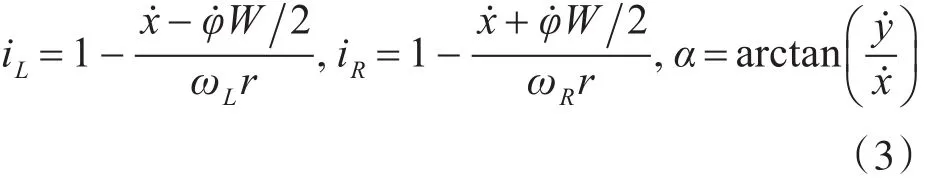
3 履带车辆动力学模型

为了方便对无人车辆进行动力学分析，现作如下假设：

1）车辆在水平硬路面上进行稳态转向运动，运动过程中所受的剪切力与剪切位移有关；

2）直驶与转向过程的行驶阻力系数相同；

3）考虑无人车辆高速转向时离心力的纵向分量与横向分量的作用［16］。

4）将履带视为不可拉伸的柔性带子，不考虑履带张力对接地压力的影响。

3.1 转向惯性力

图2为车辆瞬态转向受力情况。图中ICR为瞬态转向中心，cx和cy分别为质心偏移的横向与纵向距离，CR为质心运动轨迹的旋转中心。

车辆在纵向方向和横向方向的惯性力为

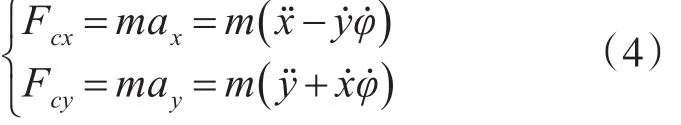
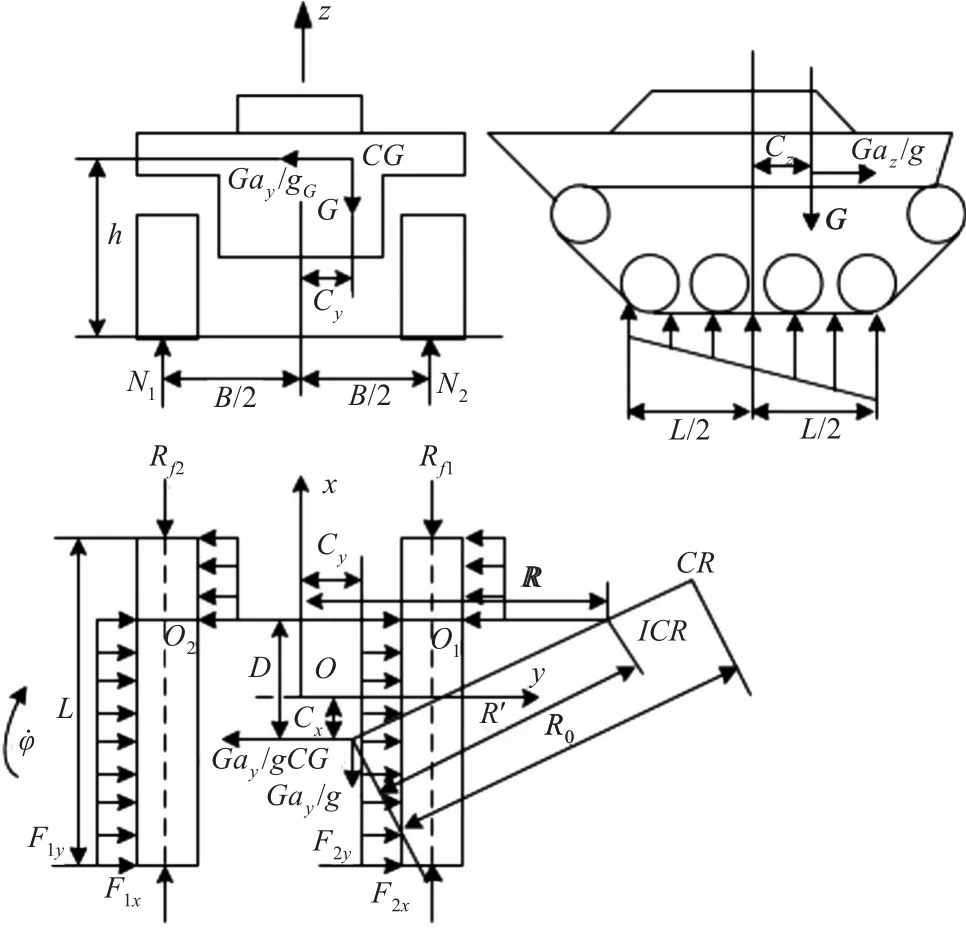
图2 履带车辆瞬态转向受力情况

3.2 履带-地面相互作用力

3.2.1 履带-地面法向作用力

转向时惯性力的横向分量Fcy使得高速侧履带接地段的法向负荷减小，低速侧履带接地段的法向负荷增加。分别表示如下：

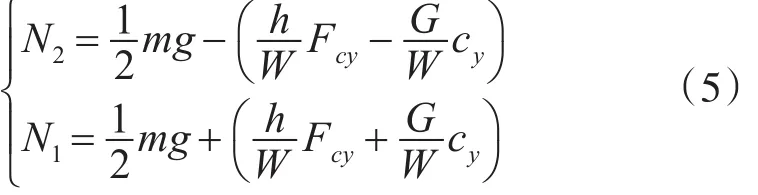
履带接地段压力分布与地面状况相关，松软地面下载荷均匀分布，坚硬地面下载荷主要集中在负重轮正下方，类似于集中载荷，高、低速侧接地段压力分布为

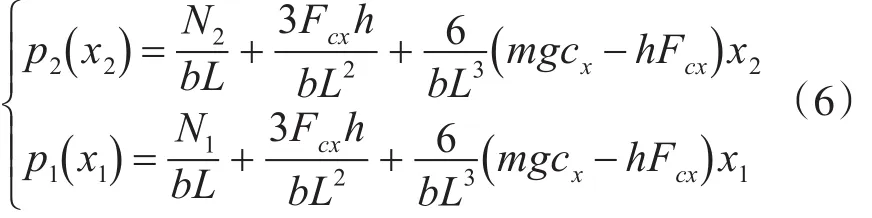
3.2.2 履带-地面剪切力

当履带车辆在坚硬路面下运动时，履带接地段的剪切力与剪切位移有关，忽略土壤的黏着系数和内聚摩擦因数等参数的影响，可以表示为

式中，μ为履带与地面之间的摩擦系数；j为履带接地段剪切位移；K为剪切模量。

两侧履带接地段剪切力与滑动速度相反，单位面积下的剪切力可表示为

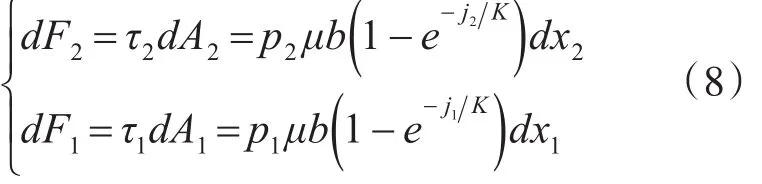
式中，b为履带板宽度。

3.2.3 履带-地面剪切位移

履带接地段任意一点（纵向坐标为x）到最前端的距离为

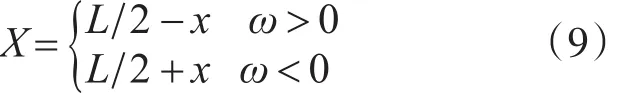
则该点运动到最前端所需时间为

式中，T为一个仿真步长，N为主动轮转速为0时经历的迭代次数。

高速侧履带（纵向坐标为x2）和低速侧履带（纵向坐标为x1）上某点瞬时滑动速度在纵向与横向方向的分量为

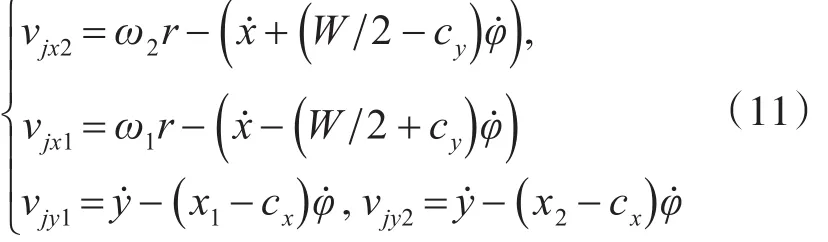
则该点处剪切位移的纵向与横向分量为

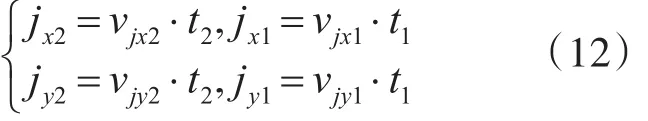
合成的剪切位移为

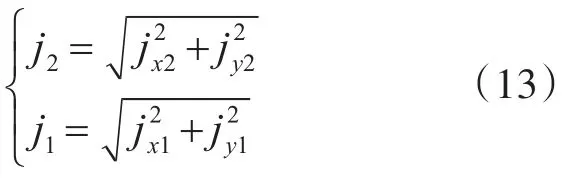
3.3 转向牵引力与制动力

令δ2和δ1分别为高速侧和低速侧履带滑动速度与纵向方向的夹角，则有

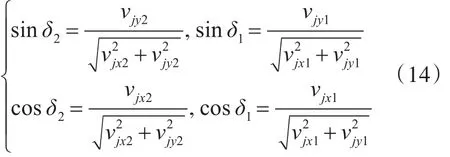
车辆稳态转向时，高速侧纵向方向与横向方向的剪切力表示为剪切力dF2、dF1在两个方向上的分量沿履带接地长度上的积分。

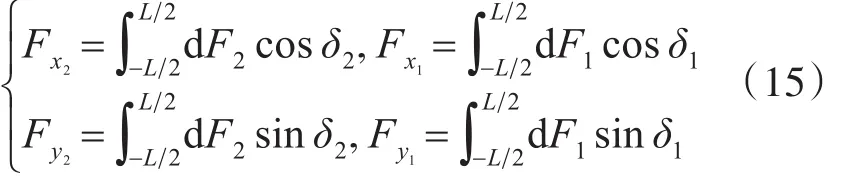
3.4 转向驱动力矩和阻力矩

驱动力矩由两侧履带纵向力分量绕车辆质心产生，高、低速侧履带的驱动力矩分别表示为

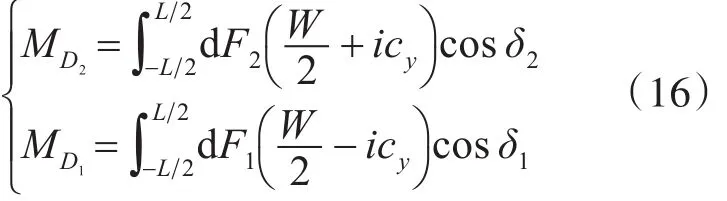
式中，W 为车体宽度；左转向时，i=1；右转向时，i=-1。

阻力矩由两侧履带横向力分量绕车辆质心产生，高、低速侧履带的转向阻动力矩分别表示为

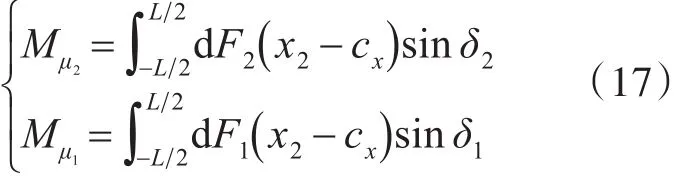
3.5 滚动阻力

高、低速侧履带滚动阻力表示为

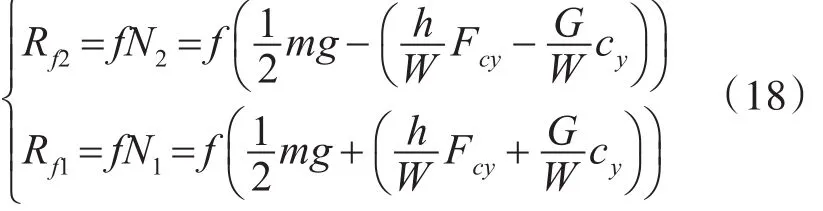
4 模型预测控制

4.1 线性预测模型的建立

与非线性模型预测控制相比，线性模型预测控制具有计算量小，求解时间短等优点，更加适用于无人车辆进行实时控制。建立的非线性系统为

将上面的连续方程进行离散化，得到

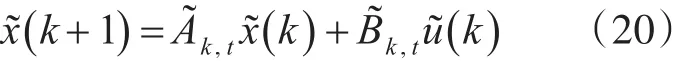
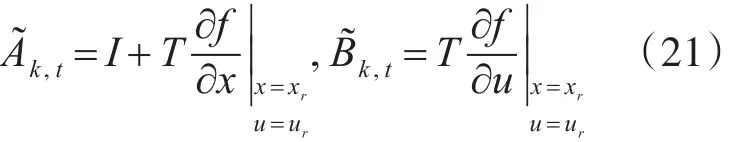
4.2 基于运动学模型的MPC算法

1）预测方程

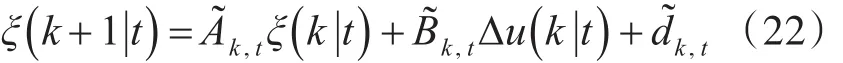
d～k，t为系统离散线性化后产生的误差，设定系统的预测时域为Np，控制时域为Nc，则在预测时域内未来一段时间的输出为

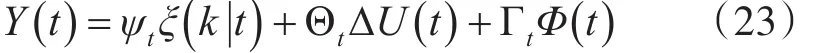
其中：

由式（23）可知，预测时域内输出量可以通过当前时刻状态量ξ(t | t)、预测时域内未知的控制增量ΔU(t)得到，需要进行预测和滚动优化。

2）优化求解

要求得控制增量ΔU(t)，必须建立合适的优化目标函数，如下式

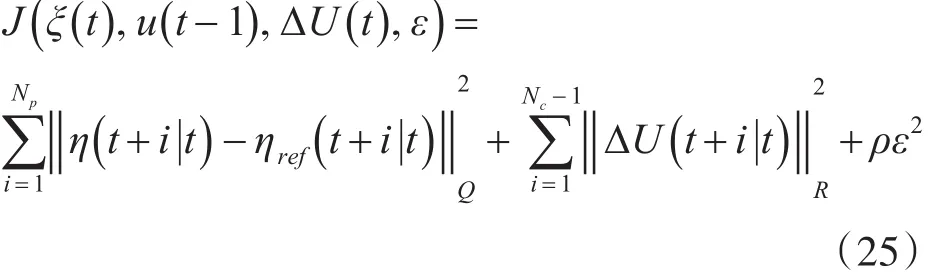
式中，Q和R为权重矩阵。第一项反应系统对参考轨迹的跟踪能力，第二项反应系统对控制量变化的约束，第三项是松弛因子，当目标函数在控制周期内无最优解时，系统会以次优解代替。经过相应的矩阵运算，目标函数可以转化为

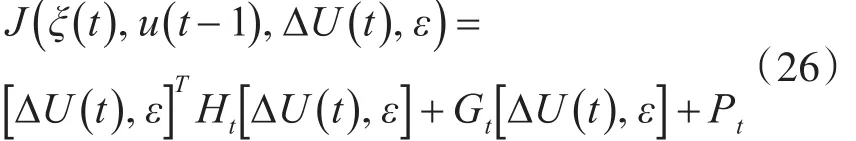
其中：

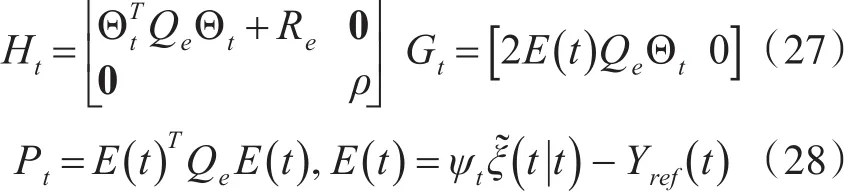
3）约束条件

这里需要考虑控制量约束、控制增量约束和输出量约束。考虑如下矩阵

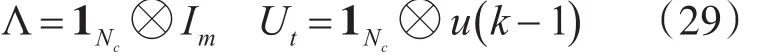
式中，m与控制量的维度相同，⊗为克罗内克积，u(k -1)为上一时刻的控制量。

建立如下约束条件

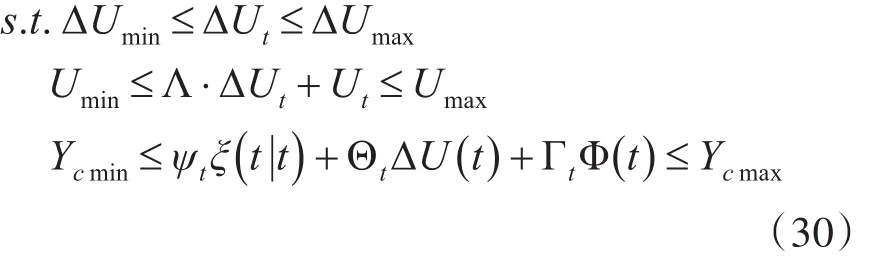
每一个控制周期内在约束条件下完成对式（26）的求解后，可得到控制增量，取该序列的第一个元素为控制输入量，可得到当前时刻的控制量为

4）仿真模型建立

履带无人车辆的参数如表1所示。

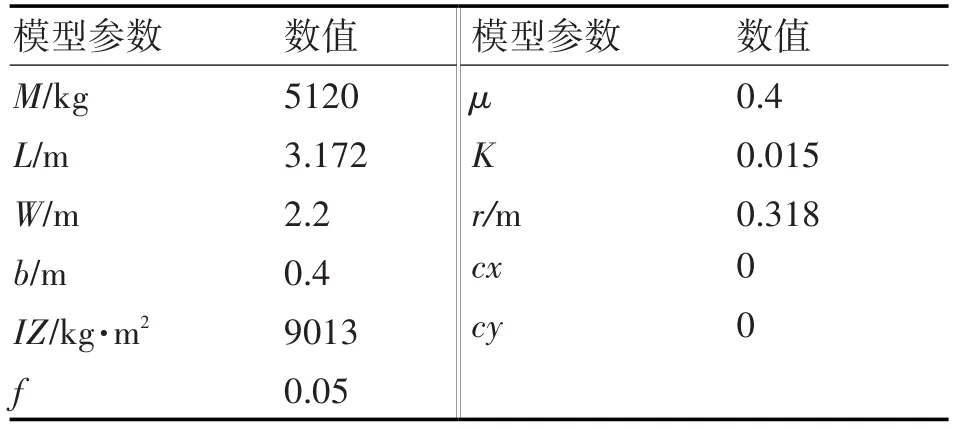
表1 履带无人车辆参数表

在Matlab/Simulink中建立车辆的动力学模型和控制器，其中，基于运动学模型的MPC控制器基于S函数编写。S-Function的输入量为位置状态量[X ，Y，φ]T，由动力学模型计算给出。输出量为两侧转速[ωL，ωR]T，通过MPC控制器的二次规划函数求最优值得到，输出给动力学模型，如此实现了闭环控制。

4.3 基于动力学模型的MPC算法

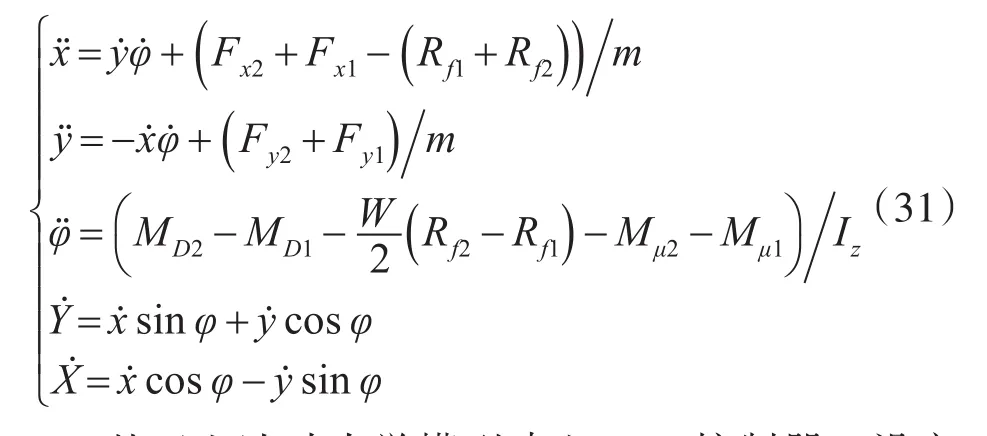
基于上述动力学模型建立MPC控制器。设定控制量约束、控制增量约束和输出量约束，如式（30）所示，采用有效集法进行求解。

5 计算机仿真与结果分析

这里设计了低速和高速时两种仿真轨迹。仿真轨迹1：0～20s为直线；20s～60s为圆形；60s～90s为双移线，初始误差：Y=3m。期望速度为3m/s。仿真轨迹2：0～15s跟踪直线，15s～35s跟踪圆弧，35s～50s跟踪直线，50s～70s跟踪圆弧。初始误差：Y=10m。期望速度为8m/s。

在车辆低速状态下，可以认为车辆不存在打滑，基于式（2）建立预测模型。基于两种模型建立控制器，进行仿真。在高速状态下，基于动力学模型（31）建立MPC算法的控制模型，仿真结果如下。

从图3和图5可以看出，两种控制器在t=10s时就能跟踪上期望轨迹，车辆跟踪圆形轨迹误差较大，原因在于车辆前进方向不断改变，车辆难以预测未来一段时间的状态变化，这可以通过增加预测时域来减小误差，但是相应会降低运算速度，影响实时性。直线和双移线航向角变化平缓，车辆能准确跟踪，X方向最大误差不超过4m，Y方向最大误差不超过2m。注意，此处的误差是轨迹误差，与路径误差不同。从图3可以看出，路径误差最大不超过0.1m。

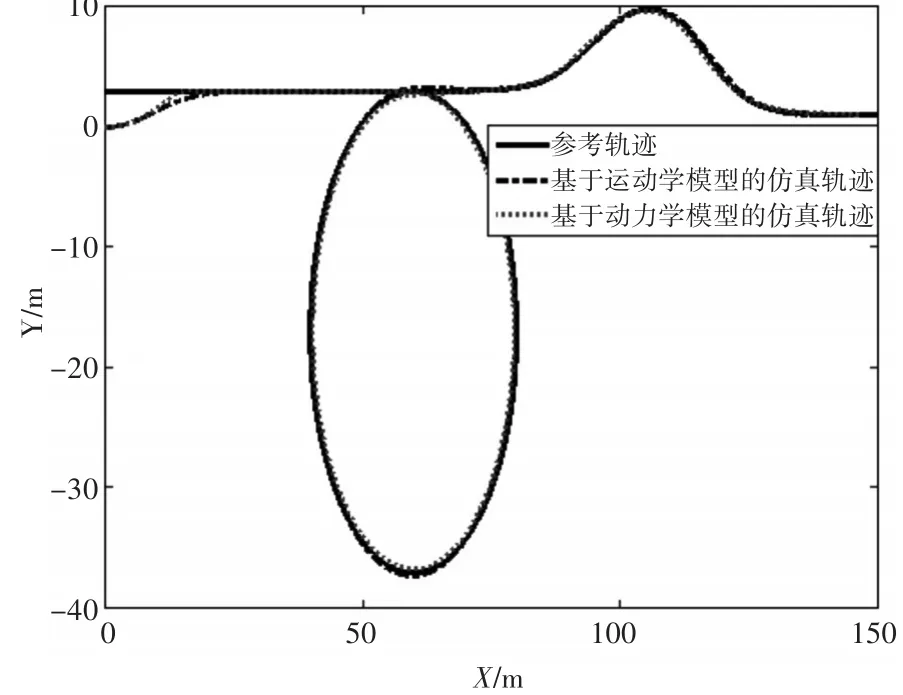
图3 低速仿真轨迹变化曲线

图4 低速时基于运动学模型和动力学模型的两侧转速变化曲线

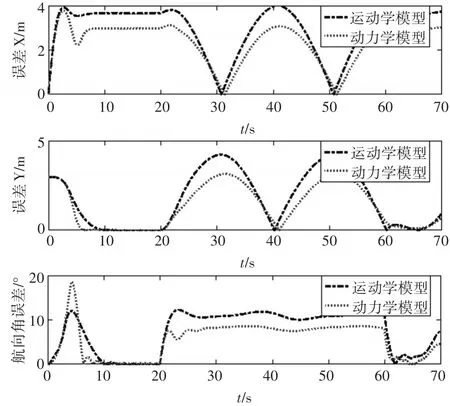
图5 低速时状态量误差变化曲线

从图4可以看出，仿真时两侧转速变化比较平滑，这主要是因为对转速增量进行了约束。动力学控制器两侧转速较高，主要是考虑了路面作用力和车辆打滑的影响，所以需要增大主动轮转速来克服打滑的影响。运动学控制器的计算时间短，实时性好，低速时可以基于运动学模型建立控制器进行轨迹跟踪。

下面是车辆高速运动时仿真结果。

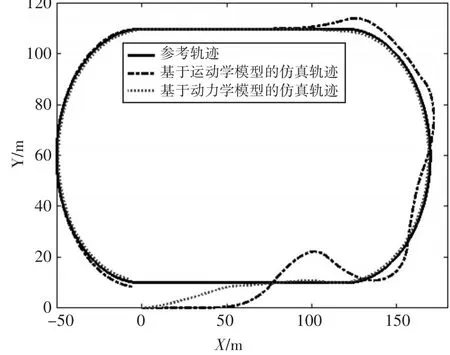
图6 高速仿真轨迹变化曲线

图7 两侧转速变化曲线

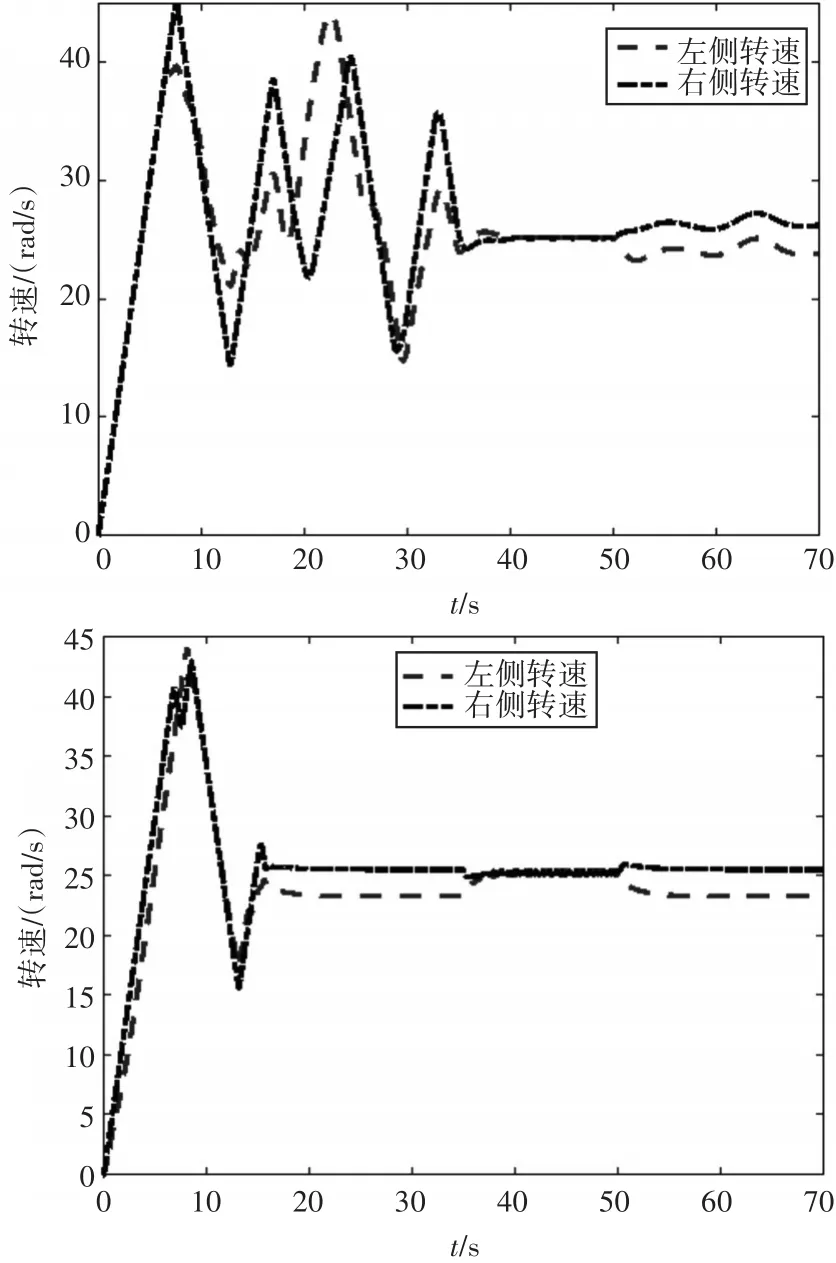
图8 高速时状态量误差变化曲线

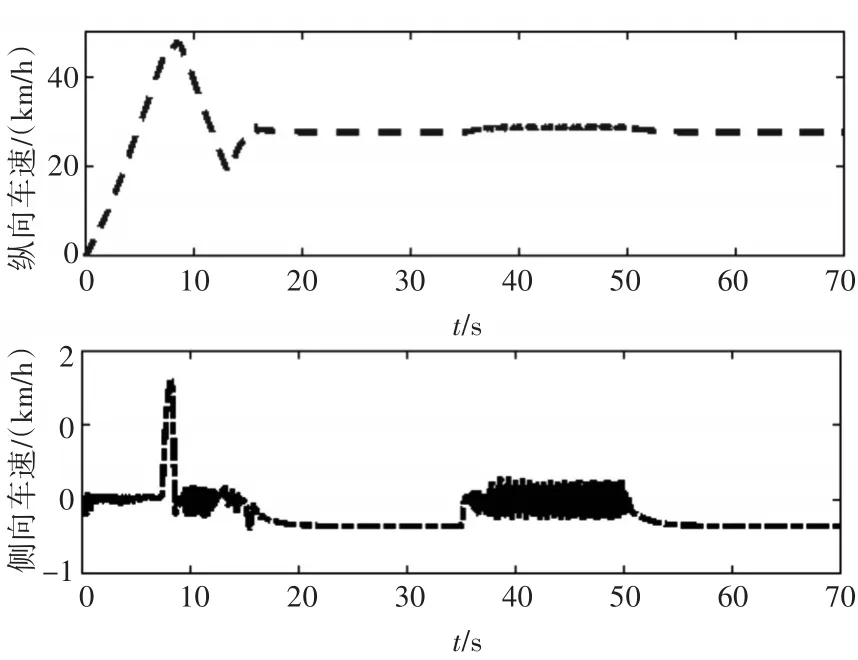
图9 纵向与侧向车速变化曲线

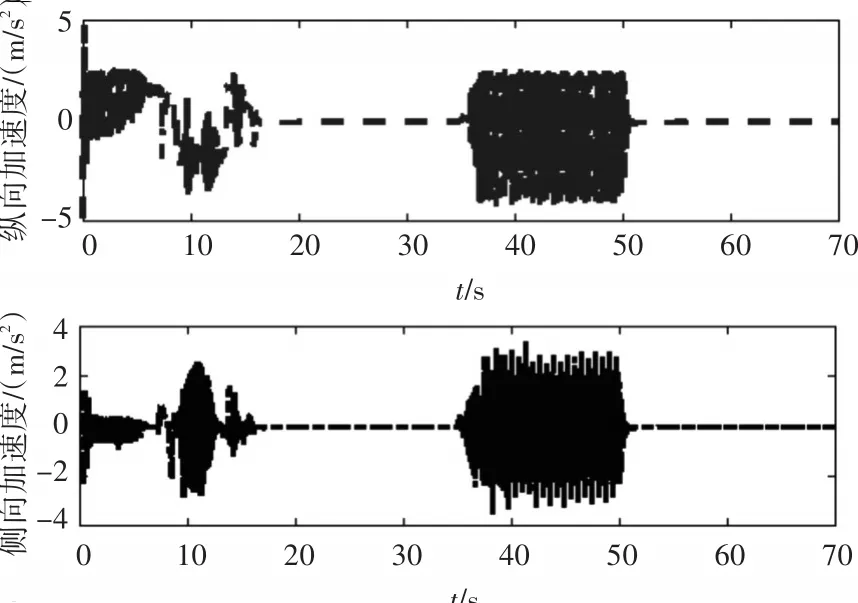
图10 纵向与侧向加速度变化曲线

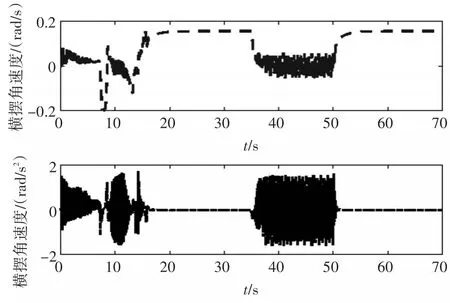
图11 横摆角速度与角加速度变化曲线

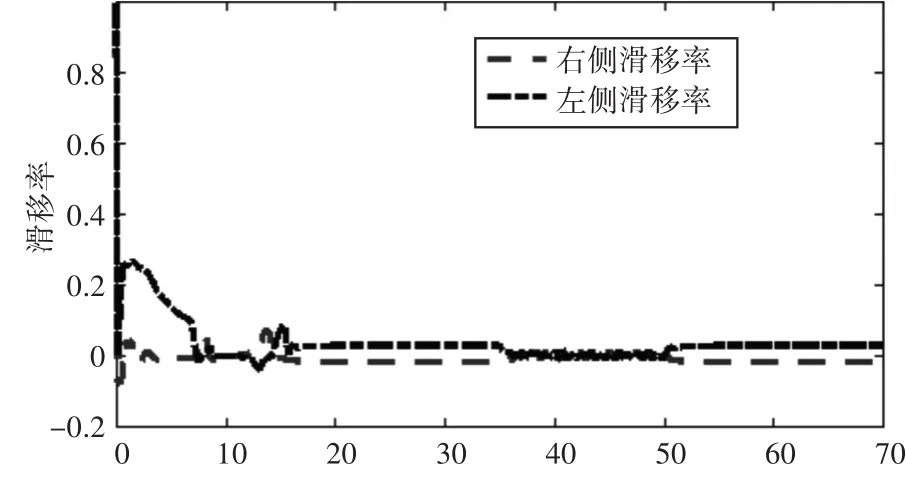
图12 滑移率变化曲线

从图7和图8可以看出，基于运动学模型建立的控制器跟踪效果较差，在40s以前会在期望轨迹附近来回摆动，X和Y方向的误差在10m左右，严重偏离预定轨迹。40s后才能沿着期望轨迹行驶，在实际过程中，难以保证车辆的行驶稳定性和轨迹可控性。基于动力学模型建立的控制器在较大初始误差条件下也能跟踪上期望轨迹，X和Y方向的轨迹误差不超过5m，在给定轨迹下能稳定行驶，不会出现跑偏和震荡现象。从图9～11中可看出，车辆在直驶过程中会出现一定的抖振现象，但幅度较小，经计算，稳定直驶时纵向车速变化幅度不超过1km/h，横向车速变化幅度不超过0.6km/h。如果减小采样频率或者地面阻力系数较小时，抖振现象会有所减弱。从图12可以看出，车辆在起步时出现了严重的打滑现象，这是因为初始误差设计较大，车辆驱动力矩大，由于惯性作用使得车辆产生了剧烈的打滑。

仿真过程中，基于运动学模型建立的控制器比基于动力学模型的跟踪误差大，车辆轨迹偏离较为严重。原因在于基于运动学模型的控制器未曾考虑地面作用力、转向离心力和滑移对车辆产生的影响，而在高速时这些参数的变化明显，使得运动学仿真模型与车辆真实情况差距很大。动力学模型较好地考虑了这些参数的影响，在仿真实验时能准确跟踪上期望轨迹，说明坚硬土路上的动力学模型建立的准确，控制算法具有良好的收敛性和稳定性。

6 结语

1）基于运动学和动力学模型建立了两种MPC控制器。Matalb仿真实验验证了算法的准确性和鲁棒性。低速时轨迹误差在3m左右，高速时基于动力学模型建立的控制器跟踪误差不超过5m。由于运动学模型没有考虑打滑率和地面作用力的影响，在高速行驶时不能够准确反映车辆的运动情况，需要基于动力学模型构建。

2）由于受打滑的影响，车辆在低速直驶过程中会出现抖振现象，可以通过增加计算精度或者在MPC算法约束条件中降低控制增量的变化率来削弱这种现象；

3）MPC算法具有滚动优化和反馈校正的优点，通过设定约束条件，可以使得控制量平稳变化，增加车辆的稳定性。

［1］Fang H，Fan R，Thuilot B，et al.Trajectory tracking con⁃trol of farm vehicles in presence of sliding［J］.Robotics and Autonomous Systems，2006，54（10）：828-839.

［2］Marino R，Scalzi S，Netto M.Nested PID steering control for lane keeping in autonomous vehicles［J］.Control Engi⁃neering Practice，2011，19（12）：1459-1469.

［3］Marcel SG，Arben C，Lesolliec G.Longitudinal Con trol for an All-Electric Vehicle［C］//Proceedings of IEEE In⁃ternational Conference on Electric Vehicle， 2012：357-375.

［4］李逃昌，胡静涛，高雷，等.基于模糊自适应纯追踪模型的农业机械路径跟踪方法［J］.农业机械学报，2013，44（1）：205-210.

［5］ Thomas Thueer，Roland Siegwart.Mobility evaluation of wheeled all-terrain robots［J］.Journal of Robotics and Autonomous Systems，2010，58（5），508-519.

［6］李岩，杨向东，陈恳.履带式移动机器人动力学模型及其反馈控制［J］.清华大学学报（自然科学版），2006，46（08）：1377-1380.

［7］李力，邹兴龙.海底机器人自动跟踪预定开采路径控制［J］.机械工程学报，2007，43（1）：152-157.

［8］孙银健.基于模型预测控制的无人车辆轨迹跟踪控制算法研究［D］.北京：北京理工大学，2015：50-60.

［9］龚建伟，姜岩，徐威.无人驾驶车辆模型预测控制［M］.北京：北京理工大学出版社，2014：72-105.

［10］Falcone P，Borrelli F，Asgari J，et al.Predictive active steering control for autonomous vehicle systems［J］.Con⁃trol Systems Technology，IEEE Transactions on，2007，15（3）：566-580.

［11］Falcone P，Eric Tseng H，Borrelli F，et al.MPC-based yaw and lateral stabilisation via active front steering and braking［J］.Vehicle System Dynamics，2008，46（S1）：611-628.

［12］ Falcone P，Borrelli F，Asgari J，et al.A model predic tive control approach for combined braking and steering in autonomous vehicles［C］//Control&Automation，2007.MED'07.Mediterranean Conference on.IEEE，2007：1-6.

［13］Falcone P，Borrelli F，Tseng H E，et al.Linear timevary⁃ing model predictive control and its application to active steering systems：Stability analysis and experimental val⁃idation［J］.International journal of robust and nonlinear control，2008，18（8）：862-875.

［14］Falcone P，Tufo M，Borrelli F，et al.A linear time var ying model predictive control approach to the integrated vehicle dynamics control problem in autonomous systems［C］//Decision and Control，2007 46th IEEE Conference on.IEEE，2007：2980-2985.

［15］陈杰，李亮，宋健.基于LTV-MPC的车辆稳定性控制研究［J］.汽车工程，2016，38（3）：308-317.

［16］王红岩，王钦龙，芮强等.高速履带车辆转向过程分析与试验验证［J］.机械工程学报，2014，50（16）：162-172.