驱动桥主减速器锥齿轮载荷的确定

郭 婷， 马贵叶， 吴 超， 毛 润

(中国北方车辆研究所车辆传动重点实验室，北京 100072)

车辆的驱动桥位于传动系的末端，其基本功用是增大由传动轴或直接由变速器传来的扭矩，将扭矩分配给左、右驱动车轮，驱动汽车行驶；并使左、右驱动车轮具有汽车行驶运动学所要求的差速功能，使车辆能够正常转向.驱动桥分为断开式驱动桥和非断开式驱动桥.非断开式驱动桥常称为贯通式驱动桥.在贯通式驱动桥中，驱动桥除有以上功能外，同时还要承受作用于路面和车架或车厢之间的垂直力、纵向力和横向力.由此可见，驱动桥不仅是车辆的动力传递机构，也是行走机构，起着支撑车辆重量的作用，驱动桥不仅承受扭矩等功率流载荷，还承受点载荷.车辆在路面上行驶，路面不同，车辆行驶状态不同，车辆行驶所需的驱动力也不同，作用在驱动桥上的功率流载荷不同；路面不同，车辆的振动等工作情况不同，作用在驱动桥上的点载荷也不同.驱动桥中最主要的传递扭矩的零件是主减速器锥齿轮，对驱动桥设计而言，要想设计出可靠性高、功率密度高的驱动桥就需要从设计入手，首先确定准确的载荷，根据载荷情况进行精细化设计，避免出现设计不足或设计过度，在生产时严格按照设计图样的要求进行实施.本研究以断开式驱动桥为例，由于断开式驱动桥只传递功率流载荷，不承受点载荷，故只对功率流载荷进行研究.

1 主减速器锥齿轮设计载荷的获取

1.1 主减速器锥齿轮等效载荷的确定

车辆的动力由发动机通过变速箱、分动箱分别传至驱动桥，通过各驱动桥再将动力分配至两端的车轮.因此，驱动桥中主减速器锥齿轮的载荷可以根据发动机载荷得到；同时，驱动桥作为终端传动部件，驱动桥主减速器锥齿轮的载荷也可根据路面情况得到.主减速器锥齿轮的设计载荷分为峰值载荷和平均计算载荷.通常峰值载荷按式(1)计算，通过发动机最大扭矩点，根据传动链上的传动比计算得到一个载荷；另一种计算方法是按式(2)计算，通过路面附着系数等参数从路面算至驱动桥得到一个载荷，将二者计算结果进行比较，选取较小的扭矩值作为驱动桥的输入峰值载荷进行驱动桥的设计.

Tje=Temax·iTL·K0·ηT/n,

(1)

(2)

式中：Tje为从发动机算至主减速器从动齿轮的扭矩；Temax为发动机最大扭矩；iTL为由发动机到所计算的主减速器从动齿轮之间的最低挡传动比；ηT为上述传动部分的传动效率，通常取ηT=0.9；K0为超载系数；n为该车驱动桥数目；G2为车辆满载时一个驱动桥给水平地面的最大负荷；φ为轮胎对路面的附着系数；rr为车轮的滚动半径；ηLB为主减速器从动齿轮到车轮之间的传动效率；iLB为主减速器从动齿轮到车轮之间的传动比.

按照式(1)、(2)求得的载荷，是驱动桥主减速器锥齿轮所承受的最大扭矩，而不是持续扭矩，因此不能作为疲劳计算的输入参数，一般用于校核静载荷.计算驱动桥的疲劳性能，一般采用平均计算扭矩进行计算，如式(3)所示.

(3)

式中：Tjm为主减速器从动齿轮的平均计算扭矩；Ga为车辆满载总重；GT为所牵引的挂车满载总重；fR为道路滚动阻力系数；fH为平均爬坡能力系数；fP为车辆性能系数.

按照以上公式进行计算，需要对公式中各系数进行选取，系数选取的是否合适直接影响着计算载荷的准确性.不同车型、不同路面，驱动桥承受的载荷也相差很大.因此，按照以上公式计算，如果不留充分的安全余量，在车辆行驶过程中，驱动桥主减速器锥齿轮有可能出现由于设计不足而导致提前损坏的情况.如果所取安全裕度过高，就会增大驱动桥的结构尺寸，造成过度设计.

在驱动桥主减速器锥齿轮载荷获取时，为了更精确地描述驱动桥的工作载荷，也可通过样车进行载荷谱测试得到路面载荷谱，进而转化至驱动桥主减速器锥齿轮上进行载荷计算.但在驱动桥初次设计时没有样机，不可能进行载荷谱测试，即使是在进行样机改进设计，载荷谱测试也要耗费大量的人力、物力等成本.在载荷谱测试后还需要将测得的载荷谱进行分析处理，才能转化为驱动桥设计所需的有效载荷谱.

1.2 驱动桥主减速器锥齿轮载荷谱确定

对于驱动桥，其工作时承受的载荷是随路面变化的随机激励，工况极为复杂，一般很难通过假设的理论载荷谱获得满意的效果.为了能更准确地得到驱动桥主减速器锥齿轮的输入载荷，需要对驱动桥主减速器锥齿轮载荷谱进行测试.要想准确测量驱动桥传递的扭矩载荷，需要将测试装置安装在传递扭矩的零件上，一般只能安装在旋转件上，但这就给导线的引出带来了困难.为避免这些问题，采用无线遥测方法.扭矩的遥测方法是将应变片贴在旋转轴上，应变片上的发射电路信号无线传输给数据采集设备中的接收电路.通过对测试应力-时间数据及转速-时间数据进行转换即可得到扭矩-时间关系.最后对时间、转速进行统计，就可得到扭矩与循环次数的关系，即驱动桥的载荷谱.图1为对样车轮边输出齿轮测试的扭矩与循环次数的关系曲线，图2为驱动桥主减锥齿轮所承受的扭矩与循环次数关系曲线.

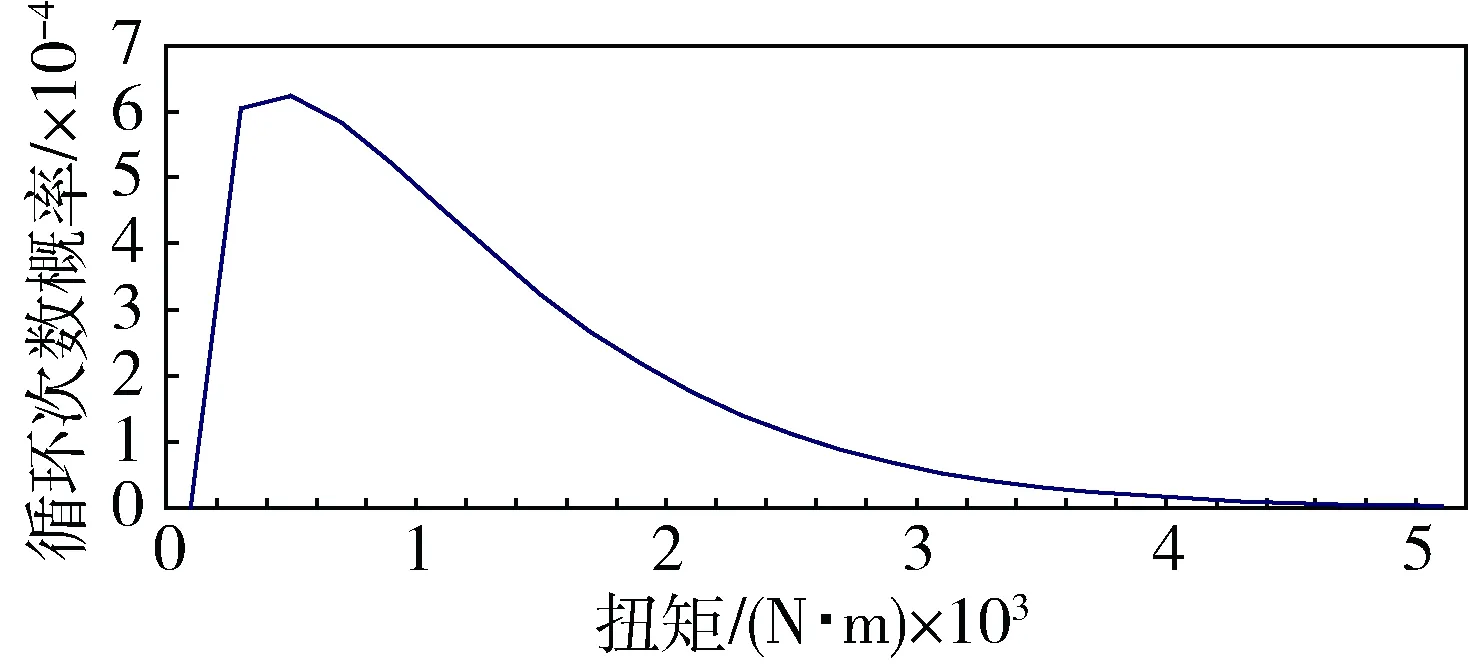
图1 样车轮边输出齿轮测试扭矩与循环次数关系曲线

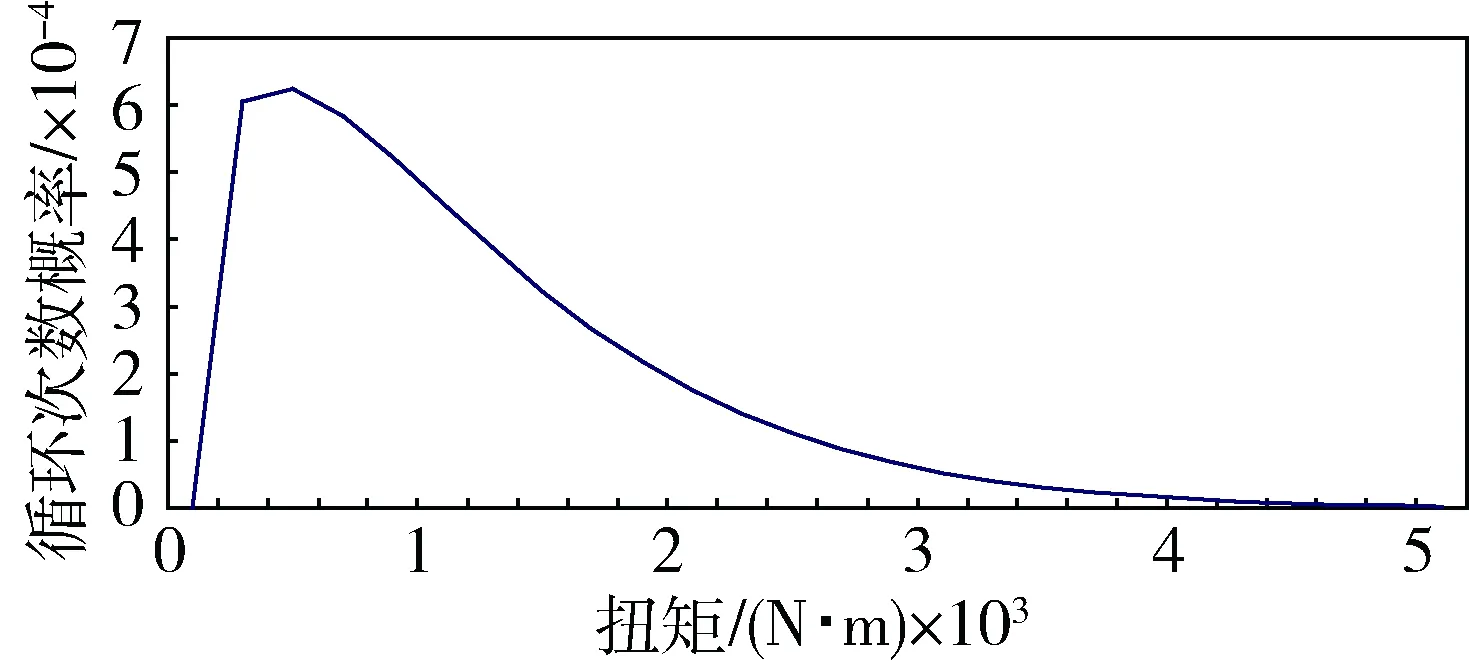
图2 主减速器锥齿轮载荷分布曲线

由图2可以看出，驱动桥主减速器锥齿轮的载荷服从三参数的威布尔分布规律.通过对测试载荷数据的分析处理，并对曲线进行拟合，得到了主减速器锥齿轮的载荷谱概率密度函数f(t).

(4)

式中：t为随机变化的载荷；β为载荷谱的形状参数；γ为载荷谱的位置参数；η为载荷谱的尺度参数；

由式(4)可以看出，驱动桥主减速器锥齿轮载荷谱的概率密度函数受形状参数、位置参数、尺度参数的影响.要想获得驱动桥的载荷谱，必须确定载荷谱的形状参数、位置参数、尺度参数.图3～图5为由式(4)得出的理想的服从威布尔分布规律的载荷概率密度函数.

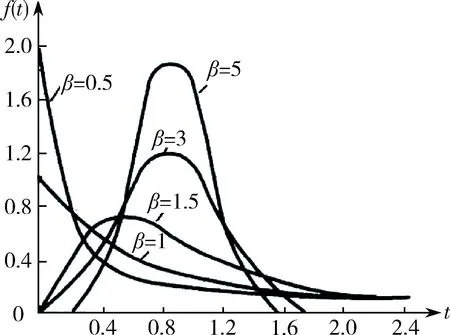
图3 形状参数对威布尔分布曲线的影响[1]

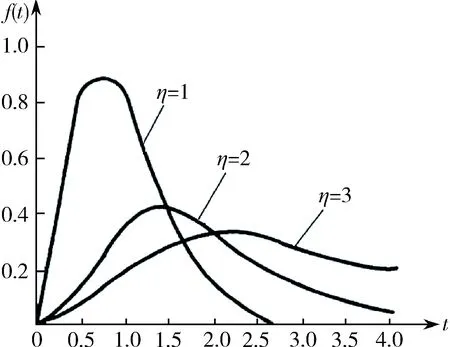
图4 尺度参数对威布尔分布曲线的影响[1]

图5 位置参数对威布尔分布曲线的影响[1]

形状参数的大小决定了概率的幅值以及概率密度的变化程度，由图3可以看出形状参数取值不同，直接影响了曲线的形状，形状参数越大，概率密度变化越快；由图4可以看出，尺度参数描述了横坐标尺度的大小，尺度参数的大小反映了载荷取值的范围.η越大曲线越平缓，载荷取值范围越宽；由图 5可以看出载荷谱的位置参数γ描述了最小载荷，确定了概率密度函数在坐标轴上的位置，γ取值不同，曲线沿横坐标左右平移，γ越小，曲线向坐标轴左边移动.

通过选取不同的参数对曲线进行拟合分析，并与测得并经过转换的驱动桥载荷谱进行比对，得到驱动桥载荷谱概率密度函数，并确定出本次所测得驱动桥的形状参数β为1.26，尺度参数η为1 180，位置参数γ为0.

2 计算两种载荷获取方法下的驱动桥寿命

2.1 等效载荷下的寿命评估

某驱动桥适用于轴重5 t的车辆，且为断开式驱动桥，驱动桥主要传动部件为主减速器，其由一对锥齿轮组成.根据整车参数，按照式(1)进行计算，得到驱动桥主动齿轮的最大计算扭矩为4 820 N·m.按照式(2)进行计算，得到驱动桥主动齿轮的最大计算扭矩为5 200 N·m，二者选取较小值，因此选用4 820 N·m进行驱动桥静强度计算.按照式(3)计算得到驱动桥主动齿轮的平均计算扭矩为2 465 N·m，选用此载荷进行驱动桥主要零部件疲劳寿命计算.采用MASTA软件，按照设计方案建立分析计算模型，对驱动桥整个系统进行计算，得到主、被动锥齿轮的疲劳安全系数如表1所示，得到主、被动锥齿轮支撑轴承的疲劳安全系数如表2所示.

表1 等效载荷条件下齿轮的疲劳安全系数

表2 等效载荷条件下轴承的疲劳安全系数

2.2 载荷谱条件下驱动桥寿命评估

将概率密度函数曲线按照阶梯型载荷进行划分成若干梯型，则这些梯形面积之和即为载荷谱的概率积分，无限趋近于1.按照图2中各载荷条件下的概率分布，根据各载荷区间的概率积分可以求出各载荷区间的循环次数配比，结合驱动桥要求的时间寿命，就能得出驱动桥在此载荷区间的工作时间.通过对载荷分布及对应工作时间的详细划分，可以有效地获取驱动桥的工作状态.根据概率密度函数曲线，按照每200 N·m的载荷划分区间进行载荷概率分配，得到某驱动桥各载荷区间下的工作时间及循环次数关系，如表 3所示.

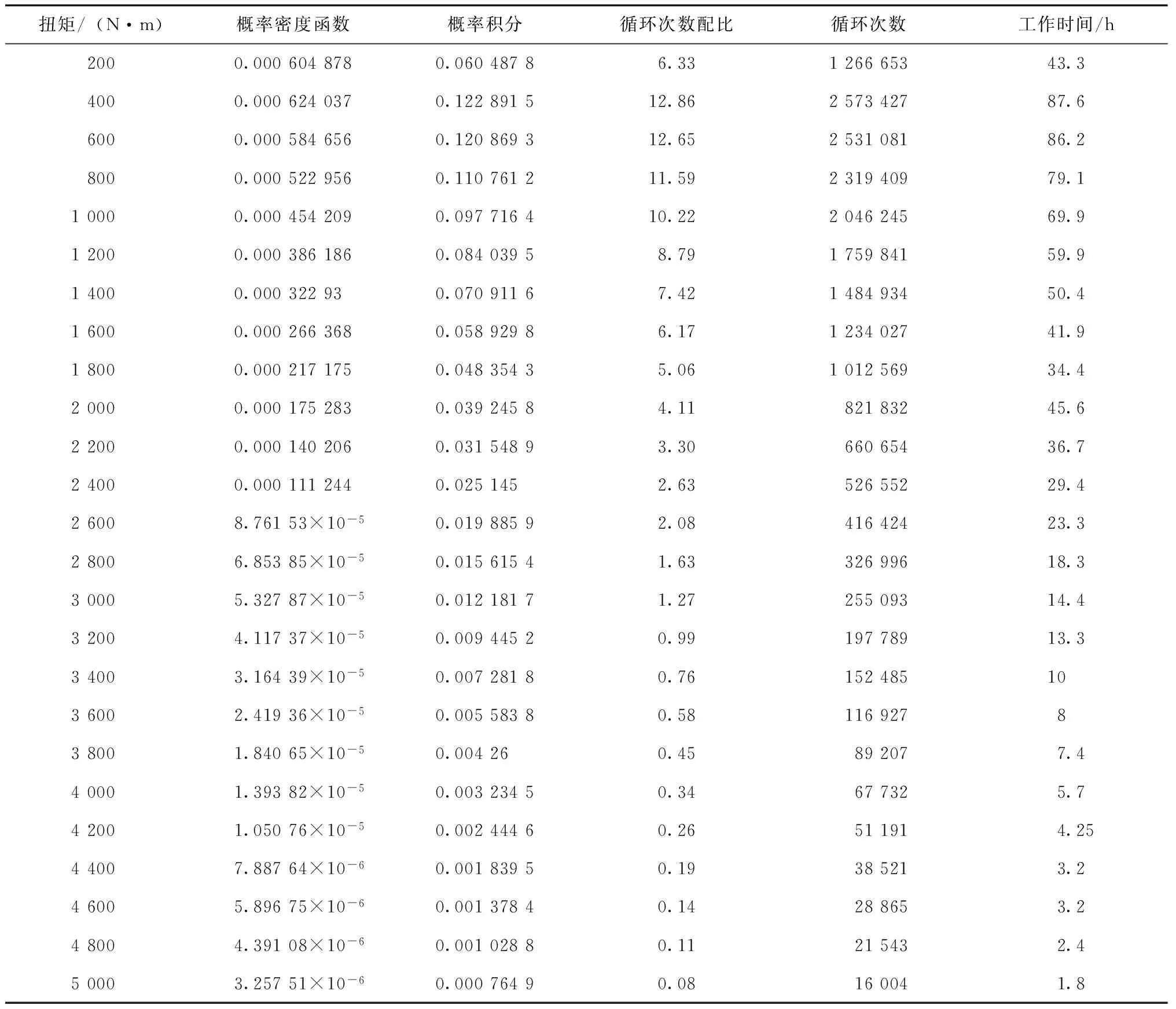
表3 驱动桥载荷谱

按照表 3中的载荷及工作时间采用MASTA软件进行驱动桥主要零部件疲劳寿命计算，得到主、被动锥齿轮的疲劳安全系数及其支撑轴承的疲劳安全系数,如表4、表5所示.

表4 载荷谱条件下齿轮的疲劳安全系数

表5 载荷谱条件下轴承的疲劳安全系数

由表4、表5可以看出，根据样车载荷谱反求出的威布尔分布载荷谱计算的齿轮弯曲强度安全系数较高，轴承的安全系数比等效载荷条件下轴承安全系数较高.

3 台架试验

对同批次两台相同参数的驱动桥分别按照等效载荷和载荷谱进行寿命试验.试验台布置如图6所示.第一台驱动桥按等效载荷计算方法，对驱动桥主动齿轮施加平均计算扭矩为246 5 N·m，循环次数2×107次.第二台驱动桥按表 3载荷谱进行加载，总循环次数为2×107次.在两次试验过程中，均未出现异常情况.在试验结束后对被试件进行分解检查，两台驱动桥中的主、被动锥齿轮、轴承均未损坏，试验后分解照片如图 7所示.由此可见，按照载荷谱方法对驱动桥寿命预估具有可行性.因此，采用等效载荷计算方法计算相对保守，求得的安全裕度较大.

图6 试验台布置

图7 试验后齿轮情况

4 结 论

通过对样车载荷谱进行测试，并对其进行转换，得到驱动桥主减速器锥齿轮载荷谱.通过对驱动桥主减速器锥齿轮载荷谱曲线进行修正、拟合，并与三参数的威布尔分布概率曲线进行比对分析，得到驱动桥主减速器锥齿轮的载荷服从威布尔分布规律.通过对某驱动桥测试载荷谱与威布尔分布曲线进行分析，得到威布尔分布概率密度函数中所需的形状参数、尺度参数、位置参数，进而得到了驱动桥主减速器锥齿轮的载荷谱概率密度分布函数.针对某驱动桥分别采用等效载荷和载荷谱的方法计算齿轮、轴承等关键零件的寿命，得到两种计算方法下零件的安全系数，结果表明：对同样的零件采用载荷谱方法计算的安全系数比采用等效载荷方法计算的安全系数高.选取相同两台驱动桥分别按照两种载荷条件进行寿命试验，结果表明：此驱动桥能够满足使用要求，验证了计算载荷谱的可行性.因此，采用载荷谱的方法对驱动桥主减速器锥齿轮设计计算载荷进行确定具有可行性.在对类似工况条件下工作的驱动桥进行全新设计时，载荷的获取可参照此概率密度分布函数进行计算载荷谱的划分，这就避免了在进行驱动桥设计时为获取精确载荷谱而必须进行样车测试而耗费的人力、物力等，防止了由于设计输入不明确导致的设计不足或设计过度的现象.

本研究所得到的概率密度函数适用于类似路面工作的驱动桥主减速器锥齿轮，若驱动桥工作的环境发生较大变化，则需要确定更适当的形状参数、尺度参数、位置参数，得到正确的概率密度函数.

[1] 凌 丹.威布尔分布模型及其在机械可靠性中的应用研究[D].成都：电子科技大学，2010