压电微喷驱动振子振动的理论分析

, ,

(上海电力学院 能源与机械工程学院, 上海 200090)

微喷是利用控制器件对微型流体进行操作,通过运用数字化控制手段,对微米级液滴进行合成和分配.由于产生的液滴直径小,利用它可以对试剂进行精确供给,在喷墨打印、微喷射以及医疗保健[1-3]等领域都得到广泛应用.压电微喷是根据压电逆效应理论,以改变密闭液体腔内体积的方式,驱动液滴从喷孔快速流出,具有响应速度快、分辨率高、稳定性好、方便控制[4]等优点.

本文基于微喷驱动振子的电-固耦合模型,结合ANSYS软件仿真,分析压电驱动振子轴向振动的幅频特性以及振子结构参数对其致动能力的影响,以提升微喷致动性能.

1 压电微喷原理与结构

本文根据压电微喷所用圆形压电薄膜的结构形式,对其进行振动分析.图1为基于压电微喷的液滴发生器模型,上层为压电驱动部分,由压电陶瓷和单晶硅薄膜复合而成;中间为液体腔部分,腔体内有流体,腔体一侧设置有进液口;下层为喷孔面,面上有沿圆周分布的圆孔.

图1 压电微喷工作原理与结构示意

当驱动结构处于工作状态时,压电陶瓷片上下极板间加载具有谐振频率的电压,上下电极间形成电场,在静电力驱动下,迫使单晶硅薄膜发生谐振,进而带动密闭液体腔内流体产生周期性波动,当变形的程度足够克服液体表面张力和耗散能时,射流开始断裂形成液滴.可见,驱动振子对其液滴形成至关重要.

2 压电驱动振子的力学分析

2.1 压电振子的微分方程

压电驱动振子采用周边固支的形式,因此对于轴对称圆体结构选取柱坐标系比较方便,如图2所示,其中,a和t1分别为单晶硅层的半径和厚度,b和t2分别为压电陶瓷层的半径和厚度.柱坐标的r-θ平面位于压电驱动薄膜的底部,坐标原点为圆心,z轴为对称轴穿过压电驱动振子的中心.

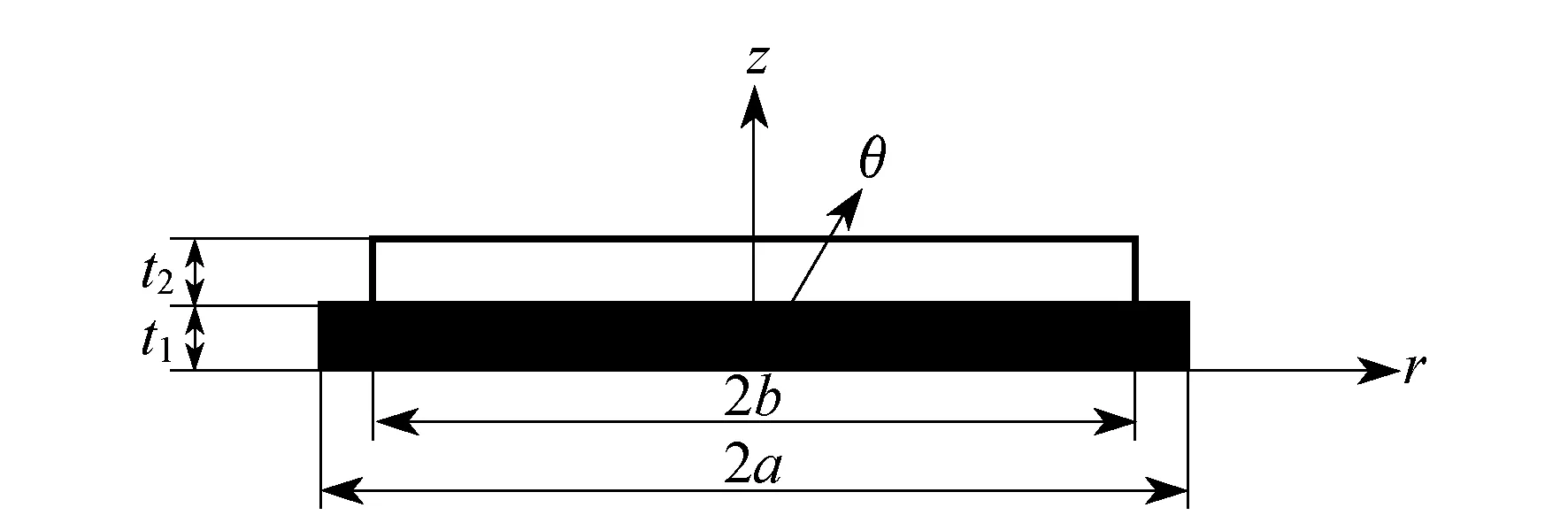
图2 压电驱动薄膜结构尺寸示意

根据弹性薄板弯曲理论以及压电复合薄膜的结构形式,可以分别求得压电陶瓷层和单晶硅层的应力和应变.

单晶硅薄膜层本构方程为:

(1)

式中:σr,σθ,τrθ——分别表示单晶硅薄膜中的径向应力分量、环向应力分量、沿径向的剪切应力分量;

E1——单晶硅薄膜的杨氏弹性模量;

μ1——单晶硅薄膜的泊松比;

w——z方向的变形位移.

压电陶瓷层本构方程为:

(2)

其中,

(3)

(4)

(5)

式中:σ1,σ2,E3——分别表示压电陶瓷层中的径向应力分量,环向应力分量,z方向的电场强度分量;

E2——压电陶瓷层的杨氏弹性模量;

μ2——压电陶瓷层泊松比;

δ33——倒介电常数矩阵分量;

g31——压电常数矩阵中的分量;

D3——z方向的电位移分量.

将E3在压电陶瓷层厚度方向积分,可得:

(6)

式中:U′——加在压电陶瓷层上的电压.

2.2 Rayleigh-Ritz法求解

采用Rayleigh-Ritz法[5]对压电驱动膜的固有频率和振动位移进行求解,其能量方程如下:

L=Umax-Tmax-UE max

(7)

式中:Umax——系统的最大势能;

Tmax——系统的最大动能;

UE max——系统的最大电能.

在中间部分压电陶瓷沿z方向的位移设为w1,在单晶硅层和压电陶瓷层半径差之间的环向单晶硅层沿z方向的位移设为w2,系统总的弹性势能为:

(8)

其中,

(9)

(10)

(11)

(12)

系统的电能为:

(13)

通电后,对于整个系统在压电陶瓷上施加谐振电压激励,则受迫振动的位移也是谐振,并且与激励电压的频率相同,即w1=w1ejωt,w2=w2ejωt,Umax=U,UE max=UE,则Tmax表示如下:

(14)

式中:ρp——压电陶瓷密度;

ρSi——单晶硅的密度.

选取合适的位移函数,满足周边固支条件下,可知第一阶弯曲振动的固有角频率为:

(15)

位移函数为:

(16)

其中:

(22)

2.3 压电振子一阶固有频率编程计算与仿真

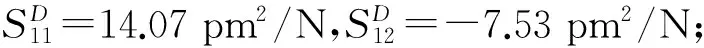
周边固支条件下,根据理论模型解析表达式,将具体参数代入,进行编程计算求解.得到压电驱动薄膜的第一阶振动的固有频率.同时,利用Ansys有限元分析软件对压电驱动薄膜进行仿真分析.理论计算第一阶振动的固有频率为38.73 kHz,模拟仿真的一阶模态如图3所示,结果为36.17 kHz,两者误差仅为6.6%,表明理论计算与仿真分析结果一致.

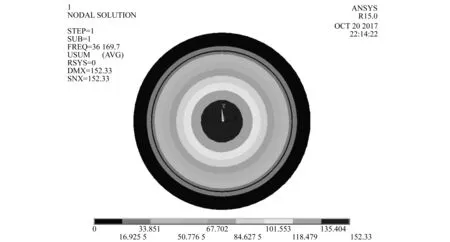
图3 一阶固有频率下压电振子模态

3 激励电压及结构参数对压电振子位移的影响

驱动控制的关键环节在于掌握压电振子的振动特性.影响振子振动特性的因素很多,本文着重研究激励电压和结构参数等影响因素对其振动特性的影响,因此分别针对不同激励电压和压电厚度以及压电振子半径比等影响因素进行静力分析,结合ANSYS仿真数据,获得不同激励及结构参数条件下的影响关系曲线.

3.1 激励电压的影响

在100 V电压驱动下,对压电振子的压电形式进行分析,t1=0.1 mm,t2=0.3 mm,得到单晶硅压电薄膜横断面上各点位移分布,如图4所示.

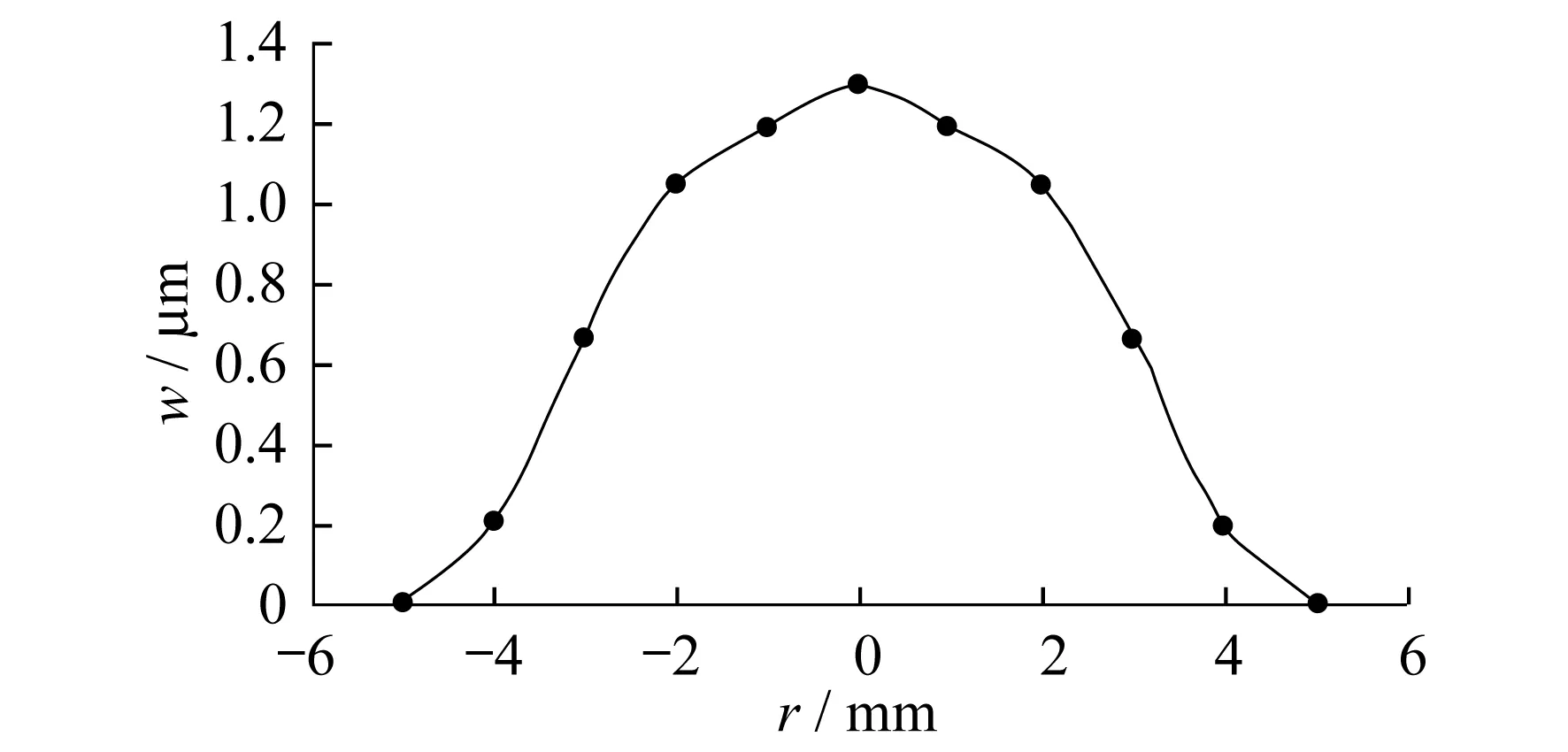
图4 压电薄膜断面上位移变化曲线

由图4可以看到,对薄膜周边固支,位移为零,中心点处的位移最大,为1.29 μm.越偏离中心点处位移越小;且位移下降的速度先增大后减小,到两边的断面处位移减小到零.总体来看,在薄膜横截面上各点处的位移呈类抛物线分布.

在振子结构尺寸不变的条件下,不同激励电压下压电薄膜的中心点位移曲线图如图5所示,位移变化随加载电压呈线性变化.

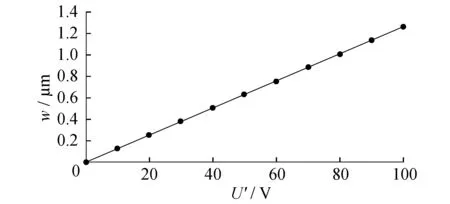
图5 压电薄膜中心点位移随激励电压变化曲线

3.2 压电厚度的影响

在其他条件保持不变的情况下,改变压电陶瓷层的厚度,压电薄膜中心点上的位移变化曲线如图6所示.由图6可知,随着压电陶瓷层厚度的增加,压电薄膜中心点整个位移曲线呈先升高后下降趋势.在压电陶瓷层厚度为0.1～0.15 mm之间时,存在一个振幅最大的点,之后振幅逐渐下降.

图6 压电薄膜中心点位移随压电陶瓷

3.3 压电振子半径比的影响

在其他条件保持不变的情况下,随着压电薄膜半径比b/a的变化,压电薄膜中心点上的位移变化曲线如图7所示.由图7可以看出,整个曲线大致呈抛物线分布,在半径比为0.85左右时,压电薄膜中心点上位移最大.半径比小于0.85时,压电薄膜振动位移随半径比的增加而增大;当半径比为0.85时,位移达到最大;当半径比大于0.85时,振动位移随半径比的增加反而减小.

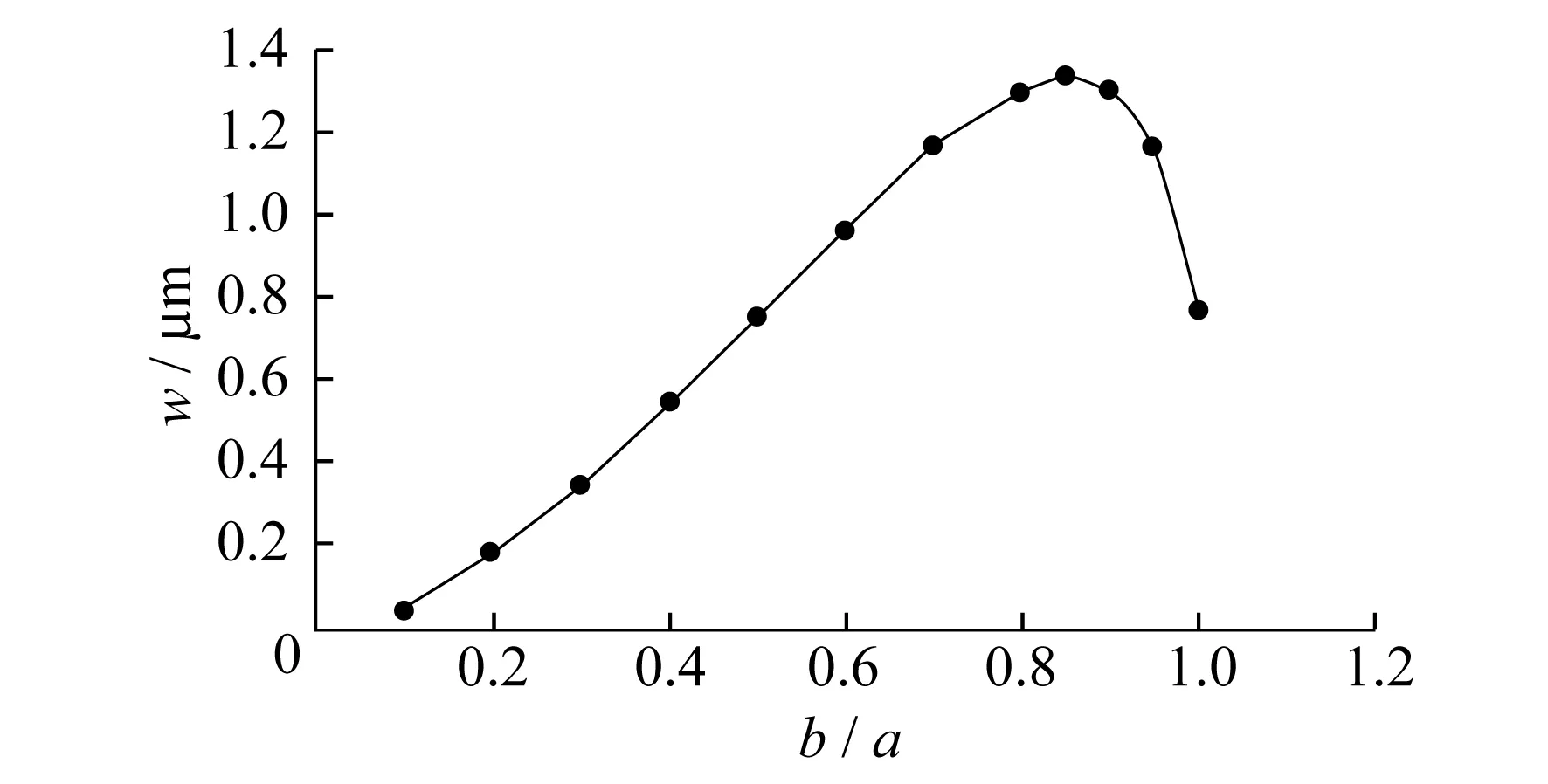
图7 压电薄膜中心点位移随压电驱动膜

4 结 论

(1) 对压电薄膜施加不同的谐振电压,驱动电压越高时,其振动位移越大,且呈线性增加,但根据实际情况,考虑薄膜的强度限制,驱动电压不宜过大,应设置在薄膜可承受的范围内;

(2) 压电陶瓷层的厚度和膜片中心点位移关系表明,随着压电陶瓷层厚度的增加,整体上膜片在压电作用下变形产生的位移逐渐减小,但在一开始压电层厚度较小时,随着压电层厚度增加,存在一个厚度值使振幅达到最大;

(3) 压电薄膜半径比和膜片中心点位移关系表明,随着压电薄膜半径比的增大,膜片中心点位移先逐渐增大,之后逐渐减小,减速较快于加速,整体上呈类抛物线形式,且在0.85左右存在一个峰值.

[1] THOKCHOM A K,ZHOU Q,KIM D J,etal.Characterizing self-assembly and deposition behavior of nanoparticles in inkjet-printed evaporating droplets[J].Sensors and Actuators B:Chemical,2017,252:1063-1070.

[2] JO I S,CHUNG M C,KIM S M,etal.Experimental investigation and hydraulic simulation of dynamic effects on diesel injection characteristics in indirect acting piezo-driven injector with bypass-circuit system[J].International Journal of Automotive Technology,2015,16(2):173-182.

[3] YOH J J,JANG H,PARK M,etal.A bio-ballistic micro-jet for drug injection into animal skin using a Nd:YAG laser[J].Shock Waves,2016,26(1):39-43.

[4] CHEN W S,LIU Y X,LIU J,etal.A linear ultrasonic motor using bending vibration transducer with double driving feet[J].Ferroelectrics,2010(1):221-230.

[5] 刘品宽,孙立宁,祝宇虹,等.双压电复合薄圆板驱动器的理论分析[J].压电与声光,2002,24(2):111-115.

(编辑 桂金星)