基于量测量突变检测与拓扑约束协同的不良数据检测

,

(上海电力学院 计算机科学与技术学院, 上海 200090)

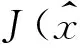
由于多个不良数据同时出现时,残差淹没使得不良数据点不会呈现任何残差特征,本文提出利用电力网络拓扑结构约束表示相关量测量之间的约束关系,对量测量突变检测方法检测出的可疑数据进行校核,从而有效避免了在不良数据辨识过程中残差污染和残差淹没的发生,提高了不良数据辨识的准确性.

1 量测量突变检测

根据相关文献可知,所谓量测量突变检测,就是将当前时刻的量测量采样值与前一采样时刻的量测量进行比较,并根据结果进行判断.如果当前时刻的量测量的某些分量发生突变,则该分量将被标记为可疑数据.该方法基于以下两个假设:一是前一采样时刻相对于当前时刻的数据经检测(或已修正)是可靠的;二是在两次采样的时间间隔内,电网结构不发生变化.

简单来说,实际量测数据的某一分量是否发生突变,是由当前采样时刻(即tk时刻)实际量测量zk,i与基于上一时刻(即tk-1时刻)的实际量测量对当前采样时刻(即tk时刻)所作的一步量测预测值zk|k-1,i之差是否超过某一阈值而确定的.当式(1)成立时,即认为该量测量发生了突变,并将其标记为可疑数据.

Δzk,i=zk,i-zk|k-1,i≥εi

(i=1,2,3,…,m)

(1)

式中:Δzk,i——第i个量测增量;

zk,i——tk时刻的第i个实际量测量;

zk|k-1,i——基于tk-1时刻的第i个量测量对tk时刻所做的一步预测值;

εi——检测门槛值.

假设电力系统的准稳态模型和量测量模型为:

xk=xk-1+Δk-1

(2)

zk=h(xk-1)+vk

(3)

式中:xk,xk-1——tk,tk-1时刻的n维状态矢量;

zk,h(xk)——tk时刻的m维量测矢量和m维非线性量测函数;

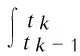
vk——m维量测误差矢量的随机序列,假定为零均值的正态白噪声序列.

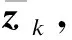
h(xk-1)+H(xk-1)Δk-1+vz,k

(4)

式中:vz,k——正常量测下,m维量测误差矢量的随机序列.

结合tk-1时刻的量测方程,将式(4)进一步写成:

(5)

(vz,k-vz,k-1)

(6)

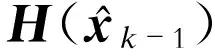
(7)

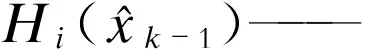
将Δzk|k-1,i写成标准化正态变量的形式为:

(8)

(9)

假设检验方法如下:

(10)

式(10)表示,当实际量测量zk,i与量测的一步预测值zk|k-1,i之差的有名值超过4σi时,即被作为可疑数据而检测出来.

2 网络拓扑约束下量测量间的关系

2.1 道路支路关联矩阵的建立

某7节点电力网络结构系统如图1所示.

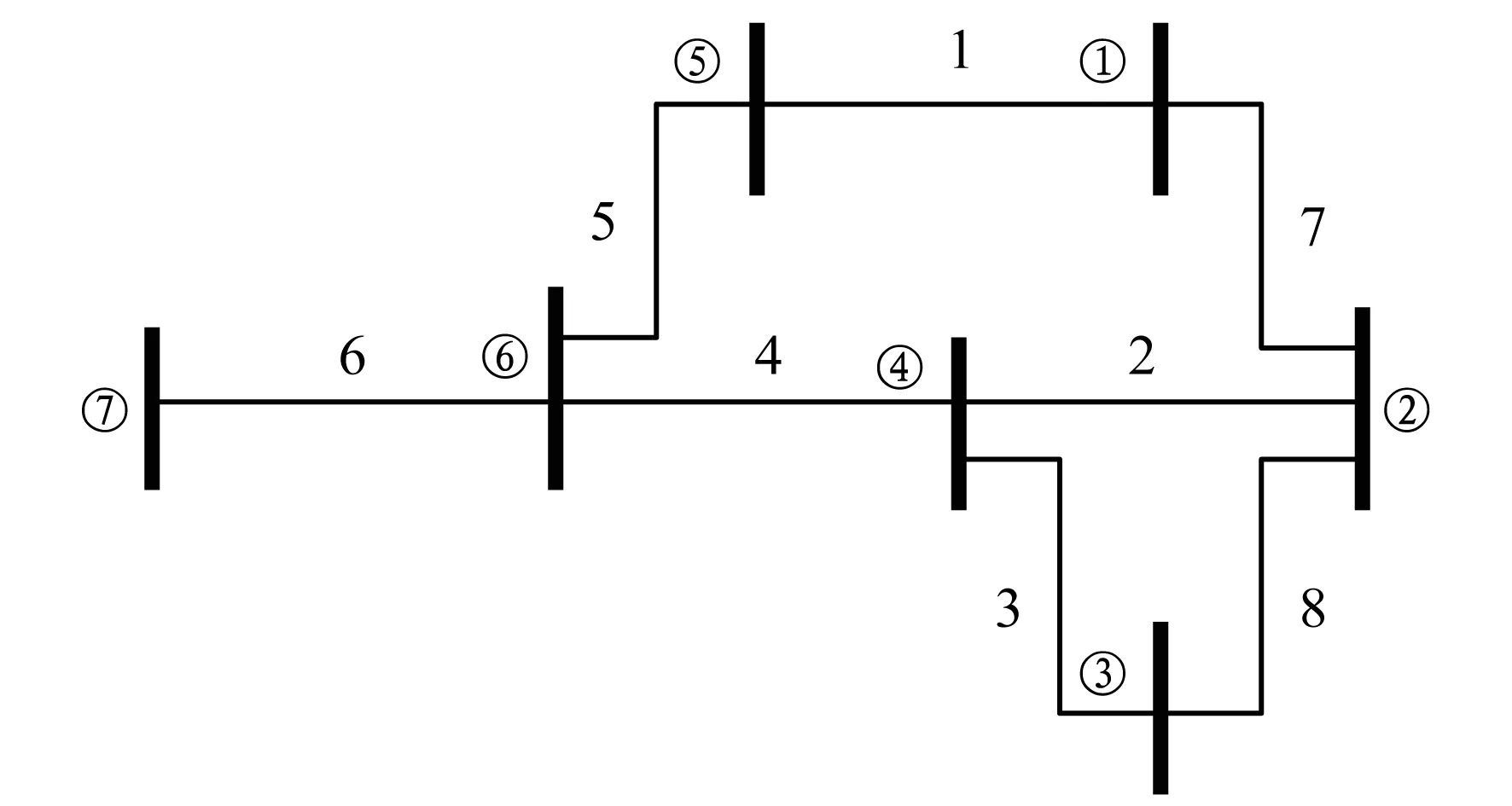
注:①～⑦—节点;1～8—支路.

图1某7节点电力网络结构示意

将图1中编号最大的母线节点规定为根节点,其余节点按照距离根节点的远近依次进行编号,离根节点最远的点编号最小;取(树枝)支路两端数目较小的编号作为该支路的编号,选定支路7,8为网络的连支,其他为树枝.

定义节点注入电流为In,节点电压为Un,支路电流为Ib,支路电压为Ub,连支电流为IL,则网络功率的量测量之间符合以下约束关系:

UbBTIL+UnTTIn=UbIb

(11)

式中:B——回支关联矩阵;

T——道路矩阵.

式(11)表明,支路功率是由两部分组成:一是节点注入功率对在道路上的支路的贡献;二是连支电流对在道路上的支路的贡献.

在没有连支或连支功率流动为零的情况下,则有:

(12)

2.2 构造量测量间线性组合关系

按照图1所示的网络,支路1至支路6为该道路的树枝,其余为连支,则可得出此时网络对应的树,如图2所示.以有功功率P为例来说明几种量测间的组合关系,假定节点⑤有功率注入(或流出).

2.2.1 节点有注入(或流出)时量测量间的组合关系

假设图2中节点⑤处有注入(或流出)功率,对于该节点所涉及的支路量测量的关系,可以表示为:

P15-P56+P5=0

(13)

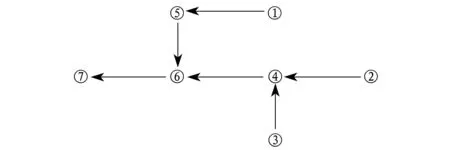
图2 7节点网络对应的树

2.2.2 含连支回路的支路量测量间的组合关系

图1中,由树枝支路1,支路3,支路4,支路5和连支支路7,支路8组成的回路,将连支所在支路的潮流量按注入/流出关系转移到该支路两端节点上,其支路量测量之间的关系可以表示为:

P12Z7+P23Z8-P34Z3+

P46Z4+P56Z5-P15Z1=0

(14)

式中:Zi——各支路阻抗,i=1,3,4,5,7,8.

由于不良数据引起的误差较大,故式(14)可以满足检测的基本要求.

2.2.3 系统的注入流出潮流量的组合关系

图1中,该系统注入功率应该恒等于流出功率与线路损耗之和.为了便于计算,在满足精度要求的前提下,根据先前系统的实际运行情况,此时注入功率P注入,流出功率P流出,损耗P损耗之间的关系可以表示为:

∑P注入=∑P流出+∑P损耗

(15)

∑P注入≈∑P流出+α∑P注入

(16)

式中:α——系统实际运行时产生损耗的经验系数.

2.3 不良数据分析原理

按照网络的拓扑约束特性及上述几种量测量间的组合关系对已标记的可疑量测量进行相关校核,由此可以辨识出真正的不良数据.特勒根定理指出:任意一个电力网络中所有支路上的电压与电流的乘积的代数和为零[10].

对于向量形式的电压电流关系,有:

(17)

3 算例分析

以4节点系统为例,其测点配置如图3所示.图3中4节点系统的量测数据如表1所示[10].运用MATLAB软件对表1中的数据进行不良数据检测分析.另外,此处还列举了加权残差法rw和标准化残差法rN对该4节点系统含有不良数据情况下的检测结果.

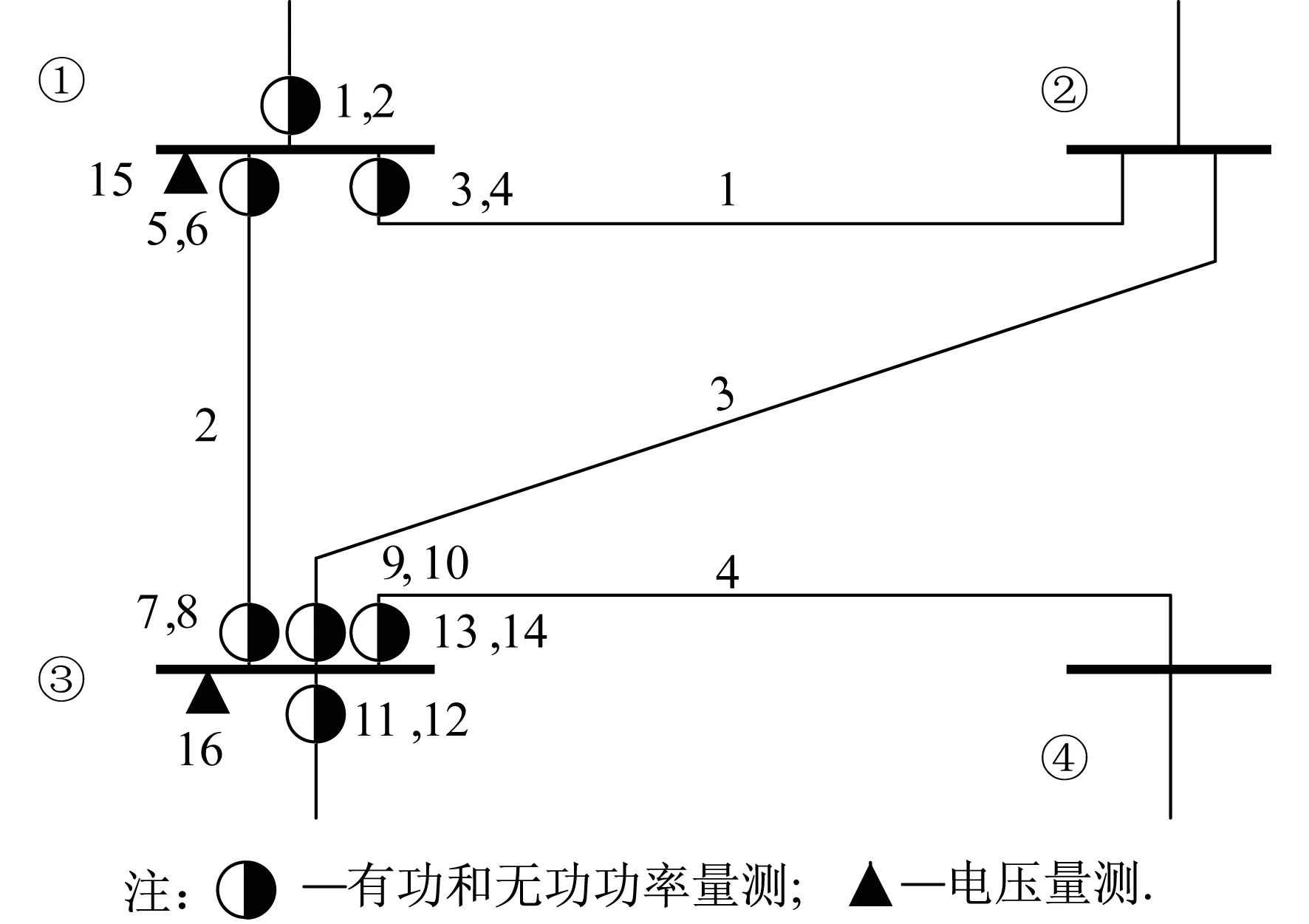
图3 4节点系统接线示意及测点配置情况

表1中数据均为正常量测量,下面根据不良数据的具体存在形式进行假设.

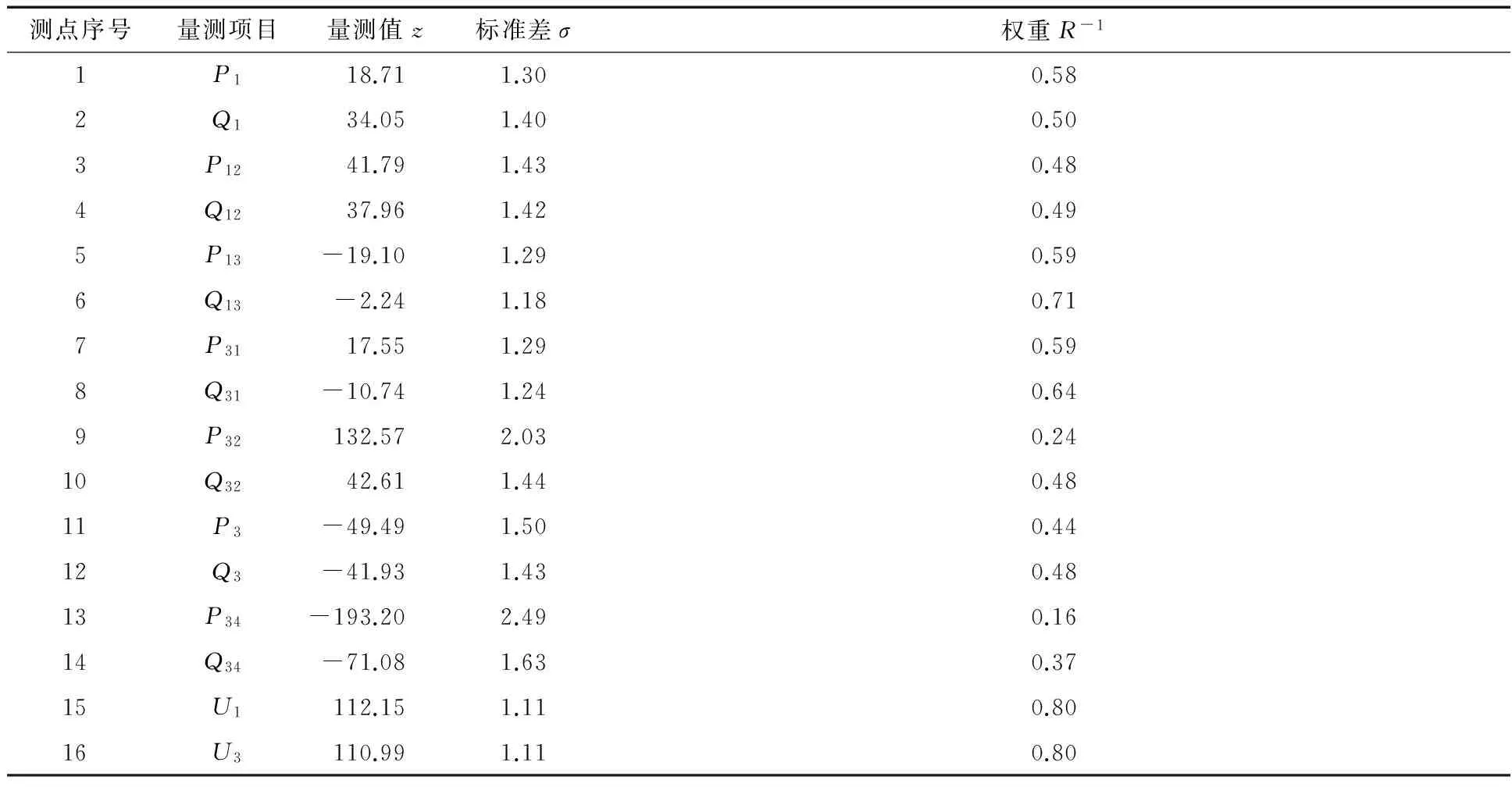
表1 4节点系统的量测数据

3.1 存在1个不良数据的情况

3.1.1rw法和rN法的检测

当系统仅含1个不良数据时,假设P1测点包含不良数据,并设置其值为28.71 MW,利用加权残差法rw和标准化残差法rN对该系统中的不良数据进行检测,结果如表2所示.

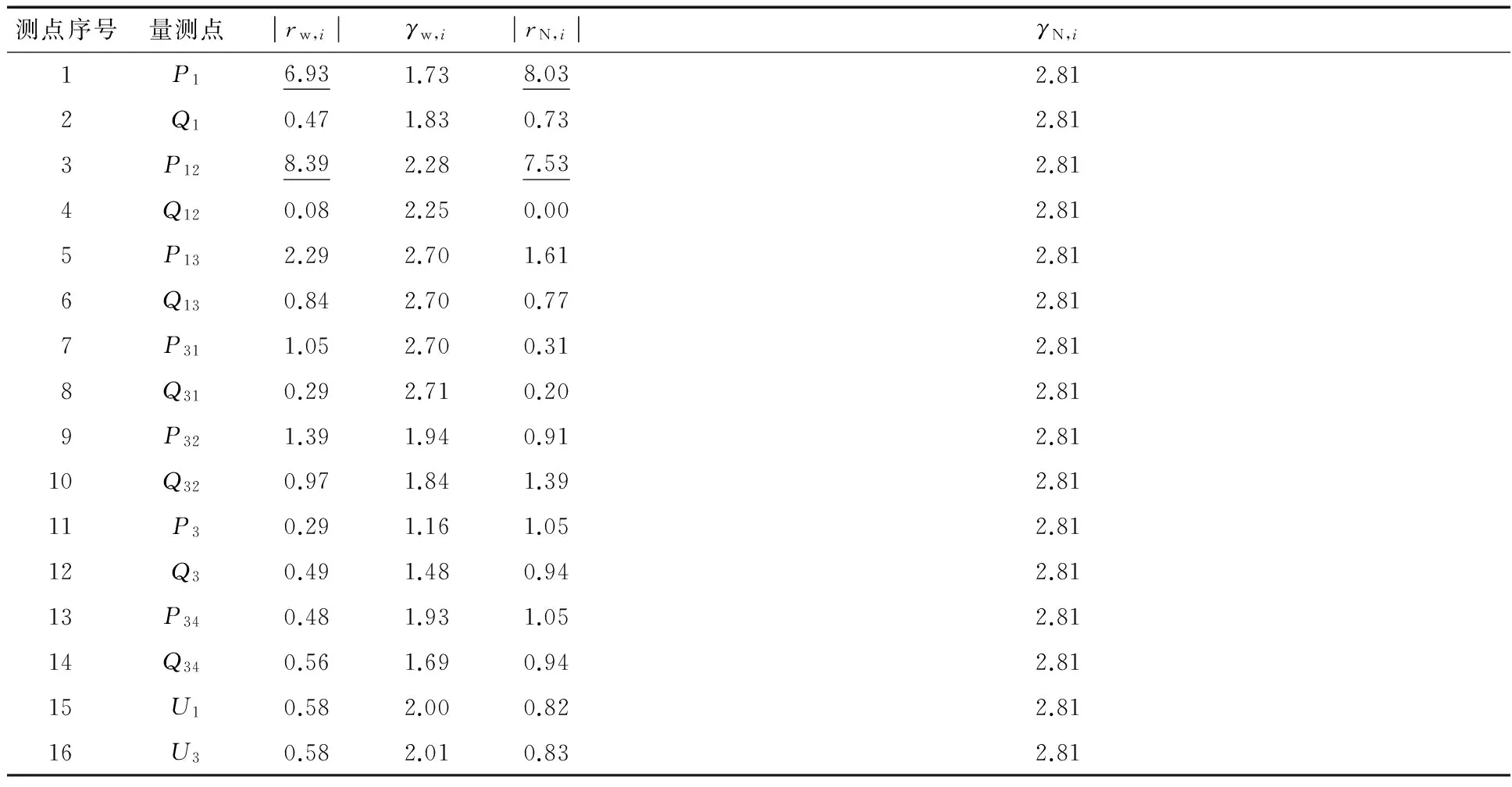
表2 存在1个不良数据时rw法和rN法检测结果

由表2可知,由于量测项目P1和P12的加权残差和标准残差均大于其相应的阈值,因此被检测出来.这说明在量测系统采样中存在不良数据,并且检测出P1和P12测点包含可疑数据.虽然以上两种方法的检测结果包含了事先假设不良数据的P1测点,但不能进一步确认二者中哪一个为不良数据,即除了不良数据的残差呈现出超过检测阈值的特征外,还有一些正常测量数据的残差也超过检测阈值.

3.1.2 量测量突变检测法

当系统仅含1个不良数据时,假设P1测点包含不良数据,并设置其值为28.71 MW,其他测点均不含不良数据.根据系统各测点的当前采样值zk,i,量测量的一步预测值zk|k-1,i,以及各量测量的标准差σi,并在其他测点添加服从标准正态分布的白噪声信号作为随机干扰,运用量测量突变检测法的检测结果如表3所示.

表3 存在1个不良数据时量测量

由表3可知,由于P1测点的量测突变值大于其检测阈值4σ1(即4.20),因此被作为可疑数据检测出来,在除P1外其他量测量为可信量测的基础上,利用式(13)和式(16)对P1测点进行校核,结果为不满足两式的约束关系,此时可以认为P1测点的量测量含有不良数据.

3.2 存在2个不良数据的情况

3.2.1rw法和rN法的检测

当系统含有2个不良数据时,假设P1和P12测点含有不良数据,并设置其值分别为28.71 MW和20 MW,利用加权残差法rw和标准化残差法rN对该系统存在的不良数据进行检测,其结果如表4所示.

由表4可知,利用加权残差法和标准残差法的检测结果在P1和P12测点的残差均未超过其相应阈值,而P13和P32测点的残差值却因超过设定阈值而被检测出来,从而导致检测失败.因此,当两个不良数据相互作用时会出现部分或全部不良数据点的残差接近于正常残差的现象,即残差污染,从而导致无法成功检测可疑数据.

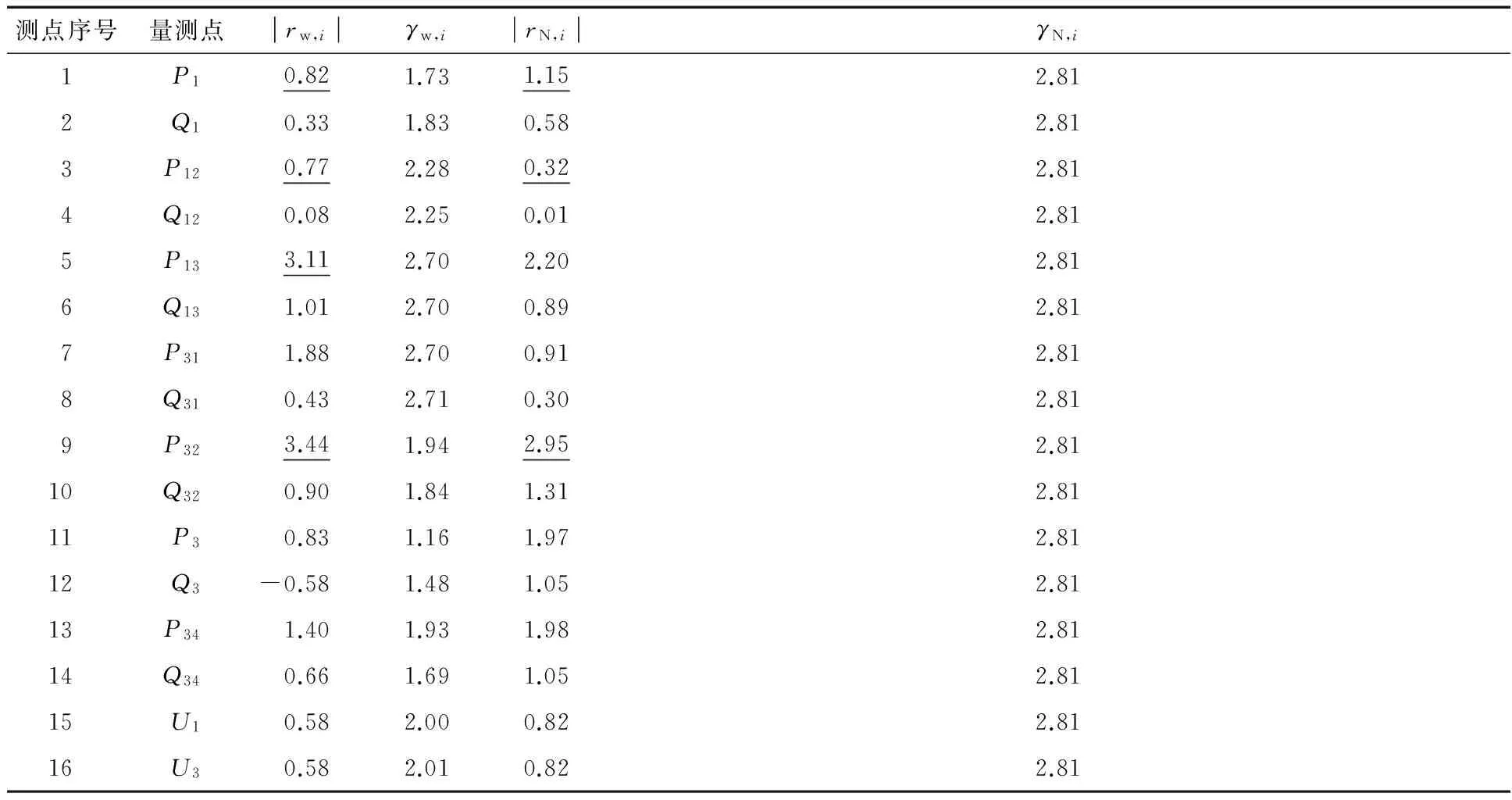
表4 存在2个不良数据时rw法和rN法检测结果

3.2.2 量测量突变检测法

当系统中含有2个不良数据时,假设P1和P12测点含有不良数据,并设置其值分别为28.71 MW和20 MW,其他测点均不含不良数据.根据系统各测点当前采样值zk,i,量测量的一步预测值zk|k-1,i,以及各量测量标准差σi,并在其他测点添加服从标准正态分布的白噪声信号作为随机干扰,运用量测量突变检测法的检测结果如表5所示.

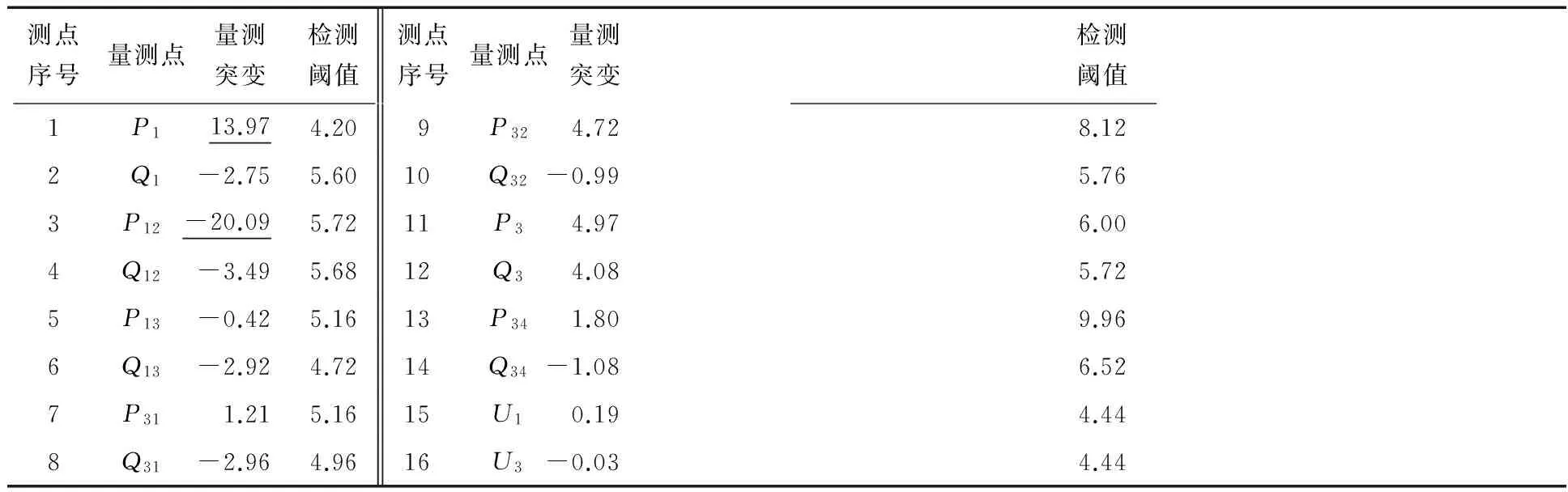
表5 存在2个不良数据时量测量突变检测法的检测结果

由表5可知,由于P1和P12测点的量测突变值大于其检测阈值4σ1和4σ3(即4.2和5.72),因此被作为可疑数据检测出来.在除P1和P12测点外其他量测量为可信量测的基础上,利用式(13)、式(14)、式(16)对P1和P12进行校核,发现其均不满足上述3个公式的要求,此时可以认定P1测点包含不良数据.由于对P12的校核涉及P1,因此根据式(17)对P1进行初步修正,其中取α为0.7%.将P1测点的数值初步修正为21.28 MW,然后利用修正后的P1及式(13)和式(14)对P12进行校核,发现其不满足两式中的关系,即可认定其含有不良数据.

利用不同方法对含有1个和2个不良数据的系统进行检测,将所得结果进行对比,并归纳如表6所示.

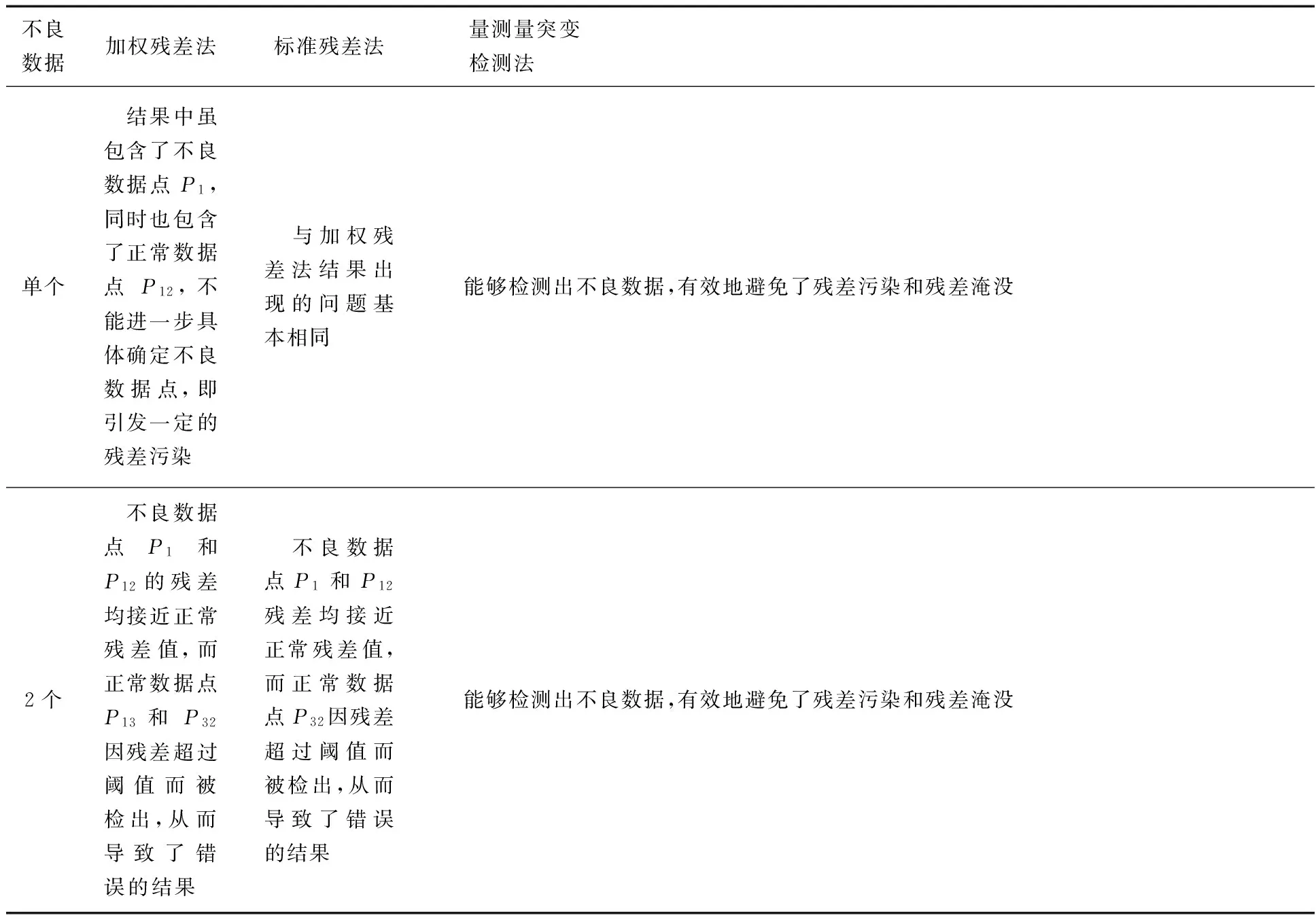
表6 3种方法的结果分析对比

由表6可知,加权残差法rw和标准化残差法rN在检测过程中出现了残差污染和残差淹没现象,从而使不良数据点被模糊,造成漏检或误检.不论假设几个不良数据点,都会使不良数据的检测失败.量测量突变检测方法在同一系统、不良数据点及其设置数值相同的情况下,实现了对单个、多个不良数据的检测.在量测量突变检测的基础上,利用关联矩阵所表示的实际系统各个潮流量的约束关系对可疑数据进行进一步校核验证,从而避免了残差污染和残差淹没的现象,降低了不良数据漏检或误检的概率,提高了不良数据检测的准确性.

4 结 语

以某4节点系统为例说明,利用3种方法对含有不良数据的系统进行检测.与传统的不良数据检测方法相比,基于量测量突变与关联矩阵协同的不良数据检测方法降低了不良数据漏检和误检的概率;避免了传统方法的残差污染或残差淹没现象;运用网络拓扑约束关系进行校核,降低了编程难度.此外,系统的量测量越多,即量测冗余度越大,就可得到较高的检测准确率.

[1] 于尔铿.电力系统状态估计[M].北京:水利电力出版社,1985:115-120.

[2] 孟建良,刘德超.一种基于Spark和聚类分析的辨识电力系统不良数据新方法[J].继电器,2016(3):85-91.

[3] 许勇.基于PMU/SCADA混合量测状态估计及不良数据检测方法[J].四川电力技术,2015(4):51-55.

[4] 张艳军,刘海珊,周苏荃.新息图拓扑可观测性及不良数据可辨识性分析[J].电力系统自动化,2008(6):55-59.

[5] 张艳军,葛延峰,高凯,等.基于广域测量系统的新息图辨识不良数据方法[J].电力系统自动化,2010(23):25-29.

[6] 张兴民,毛玉华,朱剑峰,等.利用图论方法进行多不良数据检测与辨识[J].中国电机工程学报,1997(1):69-72.

[7] 卢志刚,程慧琳,冯磊,等.基于证据融合理论的多不良数据辨识[J].电网技术,2012(1):123-128.

[8] 周小宝,罗滇生,毛田,等.一种实用的高压配电网不良数据处理方法[J].计算机工程与应用,2014(8):255-259.

[9] 董树锋,何广宇,梅生伟.电力系统状态估计中不良数据识别的新方法[C]//Intelligent Information Technology Application Association.Proceedings of the 2011 International Conference on Software Engineering and Multimedia Communication(SEMC 2011 V3),2011:4.

[10] 邱关源.电路[M].5版.北京:高等教育出版社,2006:99-102.