基于GAELM神经网络的日前电价预测

,

(上海电力学院 电气工程学院, 上海 200090)

在市场化电力交易环境中,市场参与者诸如发电企业、售电公司都需要准确地预测电价,以此作出相应的商业决策.因此,对电价预测进行研究,提高电价预测的精度具有重要的现实意义.文献[1]采用BP神经网络对Victorian电力市场进行电价预测,取得了较好的预测效果.文献[2]至文献[4]采用了不同类型的神经网络建立预测模型.基于梯度下降法的一类神经网络,具有学习速度慢、泛化能力弱的缺陷.文献[5]采用了自回归模型对美国宾夕法尼亚-新泽西-马里兰(Pennsylvania-New Jersey-Maryland,PJM)电力市场和北欧电力市场的日前电价进行建模和预测.文献[6]提出了一种单隐层前馈神经网络,也被称为极限学习机(Extreme Learning Machine,ELM).极限学习机克服了传统人工神经网络(如BP神经网络)需要大量设置训练参数、学习速度慢的缺点,已被证明在回归预测[7]等领域具有极快的学习速度和很好的非线性拟合效果.在电气工程领域,ELM算法在短期电力负荷预测[8-9]、实时电价预测[10]方面也取得了不错的效果.传统的极限学习机随机产生输入权重和隐藏节点偏置且随机产生的各参数在训练过程中保持不变,不同的参数设定会对预测精度产生影响,造成预测结果有所波动.

为了提高ELM模型的预测精度,本文提出了一种遗传算法(Genetic Algorithm,GA)优化ELM的日前电价预测方法,即基于GA-ELM神经网络的日前电价预测模型.鉴于我国电力市场的建立尚处于初步阶段,现阶段为分时电价结算,故本文采用美国PJM电力市场的历史电价数据进行建模.首先,利用GA算法,根据训练误差对ELM模型的输入权重和隐藏节点偏置进行寻优;其次,利用寻优所得最佳参数建立ELM预测模型;最后,结合PJM电力市场历史电价数据,利用ELM模型进行预测.

1 极限学习机原理

2004年,南洋理工大学的黄广斌副教授提出了一种单隐层前馈神经网络,也称为极限学习机(ELM).相比传统的人工神经网络,这种新式的前馈神经网络的隐藏层不需迭代,具有非常快的学习速度,且输入权重和隐藏节点偏置是随机确定的.

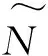
(1)

式中:βj——第j个隐藏节点的输出权重;

wj——第j个隐藏节点的输入权重;

bj——第j个隐藏节点的偏置;

oi——隐藏层的输出量.

i=1,2,3,…,N

(2)

将式(2)写成矩阵形式Hβ=T,其中:

(3)

式中:H——极限学习机的隐藏层矩阵.

通过计算线性方程组Hβ=T的最小二乘解,可求得输出权重β.

β=H+T

(4)

式中:H+——隐藏输出矩阵H的Moore-Penrose广义逆[11].

通过该计算方法可实现训练误差的最小化.

2 基于GA改进的极限学习机

鉴于极限学习机算法的特点,ELM模型的输入权重wi和隐藏节点偏置bi随机产生.当随机产生的参数值为零时,会使部分隐藏节点失效,导致模型预测精度降低.针对随机产生参数可能出现的问题,提出了GA优化ELM模型的预测方法,与传统神经网络需要对输入权重、隐藏节点偏置、输出权重都进行寻优相比,本文所提方法只需对ELM的输入权重wi及隐藏节点偏置bi进行优化选择,减少了计算量.参数寻优步骤如图1所示.

(1) 确定ELM神经网络的基本拓扑结构,对ELM模型的输入权重和隐藏节点偏置采用二进制编码,产生初始种群.每个个体均为一个二进制串,个体的维度取决于ELM模型需要优化的参数个数,即输入权重和隐藏节点偏置.

(5)

式中:θ——种群中的一个个体;

wij,bj——初始化为[-0.5,0.5]区间的随机值.

(2) 解码得到输入权重和隐藏节点偏置,将权重和偏置赋值给ELM神经网络.使用训练样本训练网络,同时使用测试样本进行测试.为使预测值与实际值的残差尽可能小,对网络设置目标函数为:

(6)

式中:n——测试样本数;

yi——预测值;

(3) 确定适应度函数以及进化代数G.适应度函数直接采用排序适应度分配函数ranking,即VFit=ranking(V).

ranking函数的计算公式为:

(7)

式中:s——压差;

Ps——个体在排序种群的位置;

d——种群中个体的数量,本文篇幅有限具体内容可以参考文献[12].

(4) 局部求解最优适应度函数VFit.逐个求解每个个体的适应度函数,根据VFit的值确定适应度较优的个体.

(5) 求解全局最优适应度函数VFit.进化代数初始值设为零,每进行一代局部最优适应度函数求解后,对适应度较优个体进行交叉、变异,产生子种群,再次计算子种群的适应度函数,并根据适应度函数值,将子种群的个体选择插入父种群,替代父种群中适应度最小的个体,得到新种群,同时进化代数进行自加一运算.当进化代数大于G时,则结束运算,计算此时的VFit即为最优适应度函数,并将其对应的参数解码,即可得到最佳输入权重和隐藏节点偏置,以此建立最优的ELM模型.

3 算例及结果分析

本文以美国PJM电力市场的历史电价数据作为算例,选取2015年10月31日至11月9日的历史电价数据对11月10日至14日进行电价预测.因PJM电力市场每小时进行一次电价结算,故一天共有24个时刻电价.在预测过程中训练样本是滚动更新的,即在进行后一日的电价预测时,将前一日的实际电价数据替换训练样本中的最旧数据.取最大遗传代数G=50,种群大小d=40,隐藏层节点数为30,激活函数为Sigmoid函数,对11月10日电价预测结果如表1和表2所示.

本文以绝对百分比误差APE和平均百分比误差MAPE作为误差评判标准.定义如下:

(8)

(9)

式中:P——实际电价;

P′——预测电价;

n——预测样本数,本文对未来24 h电价进行预测,故预测样本数为24.

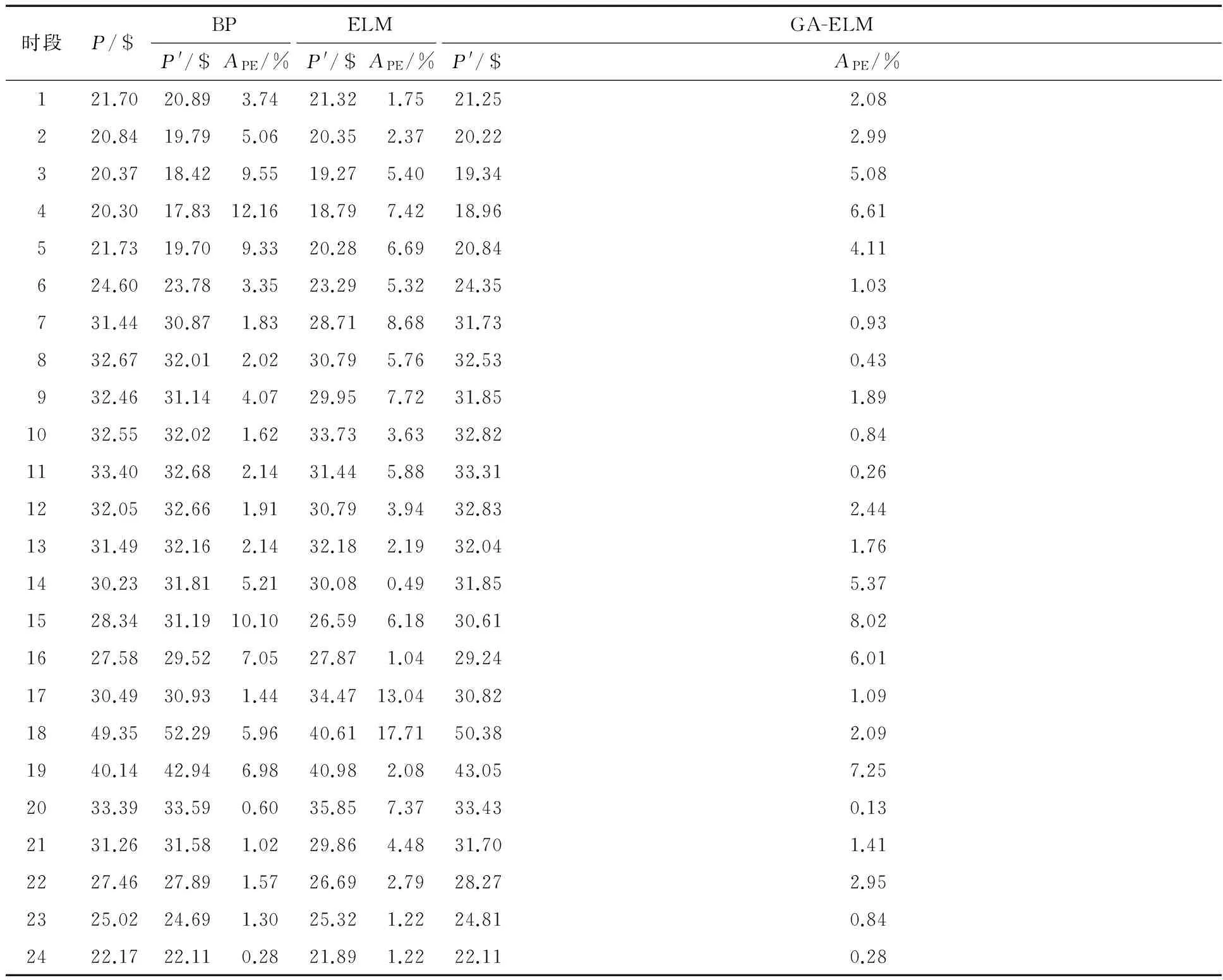
表1 2015年11月10日电价预测结果比较

表2 3种模型的MAPE和APE,MAX %

由表2可知,GA-ELM的预测精度高于BP神经网络和ELM,GA-ELM的MAPE为2.72%,低于BP神经网络的4.18%和ELM的5.18%,同时其APE,MAX也低于BP神经网络和ELM,取得了最佳预测效果.

采用上述3种模型,对2015年11月11日至14日的电价进行预测,预测结果如表3所示.

由表3可知,GA-ELM的预测精度和稳定性均优于BP神经网络和ELM,表明利用遗传算法对预测模型参数进行优化,相较于传统预测模型取得了更好的预测效果.

表3 2015年11月11日至14日3种模型的

为了进一步验证GA-ELM模型的输出稳定性和预测精度,采用上述3种模型对2017年2月13日至17日的电价进行预测,预测值曲线如图2所示.

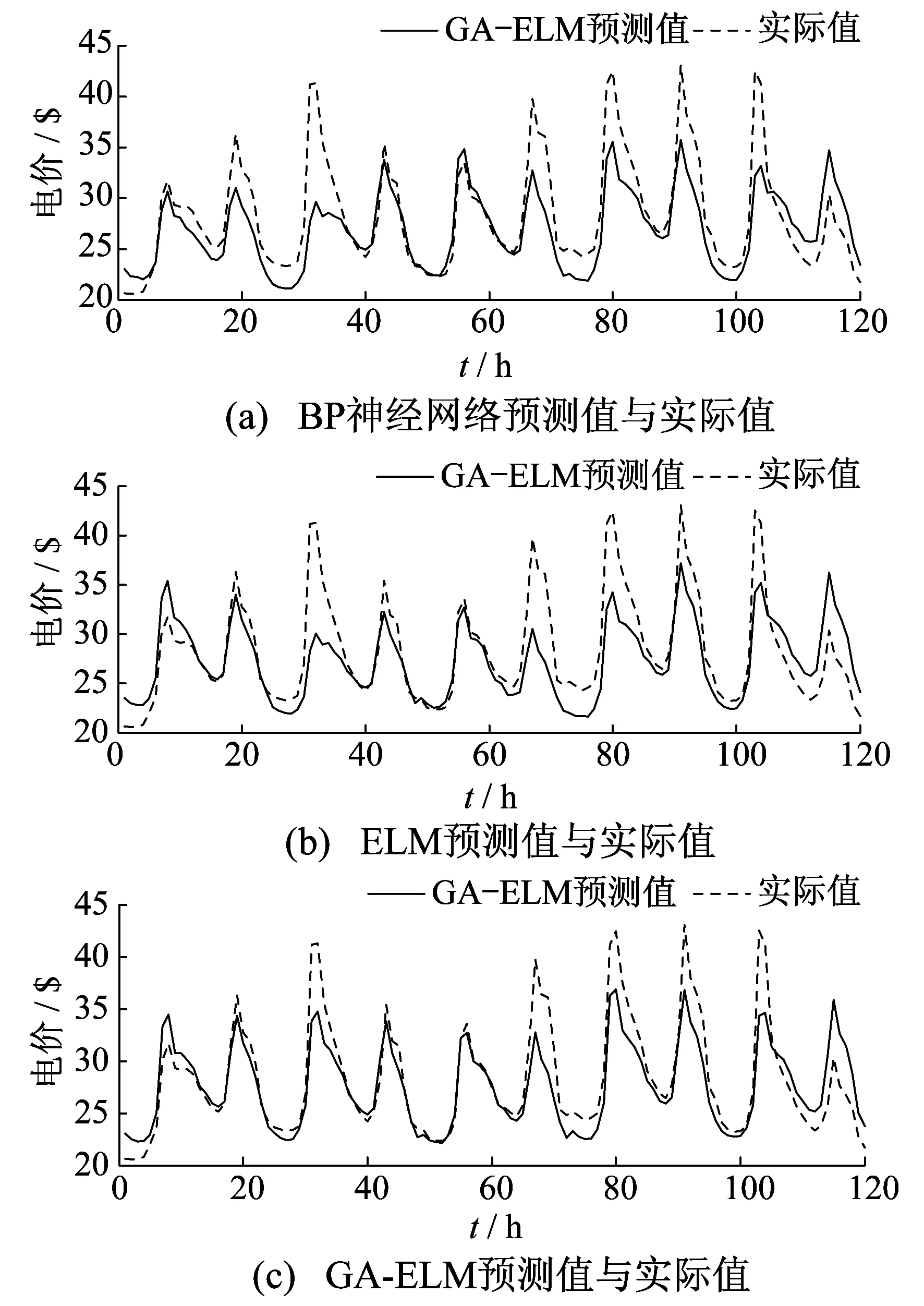
图2 2017年2月13日至17日3种模型的

利用3种模型预测2017年2月13日至17日的MAPE和APE,MAX,结果如表4所示.

由表4可知,相较于其他两种预测模型,GA-ELM具有更高的预测精度.

表4 2017年2月13日至17日3种模型的

4 结 语

本文提出一种基于GA-ELM的电价预测模型.利用遗传算法对ELM模型的输入权重和隐藏节点偏置进行优化,克服了传统ELM模型随机生成参数造成预测精度不高且波动性大的缺陷.对PJM电力市场的电价数据进行预测,结果表明,该方法可以有效地提高预测精度.

[1] SZKUTA B R,SANBRIA L A,DILLION T S.Electricity price short-term forecasting using artificial neural network[J].IEEE Transactions on Power Systems,1999,14(3):851-857.

[2] 黄羹墙,杨俊杰.基于BP神经网络与马尔可夫链的短期电价预测[J].上海电力学院学报,2017,33(1):1-3.

[3] 林其友,陈星莺,王之伟.数据挖掘技术在电价预测中的应用[J].电网技术,2006,30(23):83-87.

[4] 顾庆雯,陈刚,朱蕾蕾,等.基于遗传算法和径向基函数神经网络的短期边际电价预测[J].电网技术,2006,30(7):18-21.

[5] 刘丽燕,邹小燕.GARCH族模型在电力市场电价预测中的比较研究[J].电力系统保护与控制,2016,44(4):57-63.

[6] HUANG G B,ZHU Q Y,SIEW C K.Extreme learning machine:theory and applications[J].Neurocomputing,2006,70(1/2/3):489-501.

[7] XIA M,ZHANG Y C,WENG L G,etal.Fashion retailing forecasting based on extreme learning machine with adaptive metrics of inputs[J].Konwledge-Based System,2012,36(6):253-259.

[8] 毛力,王运涛,刘兴阳,等.基于改进极限学习机的短期电力负荷预测方法[J].电力系统保护与控制,2012,40(20):140-144.

[9] 王越,卫志农,吴佳佳.人工神经网络预测技术在微网运行中的应用[J].电力系统及其自动化学报,2012,24(2):83-89.

[10] CHEN X ,DONG Z Y,MENG K,etal.Electricity price forecasting with extreme learning machine and Bootstrapping[J].IEEE Transactions on Power Systems,2012,27(4):2055-2062.

[11] HUANG G B,ZHOU H,DING X,etal.Extreme learning machine for regression and multiclass classfication[J].IEEE Transactions on Cybernetics,2012,42(2):513-529.

[12] 雷英杰.MATLAB遗传算法工具箱及应用[M].西安:西安电子科技大学出版社,2006:76.