基于隐含信任关系的概率张量分解推荐算法

赵超， 韩立新， 杨忆,2， 何恋

(1.河海大学,计算机与信息学院，南京 211100;2.淮北师范大学,计算机学院，安庆 235000)

0 引言

随着互联网的不断发展，网络中产生的信息呈爆炸性增长，出现了信息过载的现象，在此背景下，基于信息过滤技术的推荐系统应运而生。推荐系统试图给用户推送用户可能感兴趣的物品(包括音乐、电影、图书等)。尽管传统的基于协同过滤的推荐方法[1]已经被广泛运用到像亚马逊这种大型著名公司的商业系统中，但是仍存在数据稀疏性以及预测准确性的问题。

为了缓解上述两个问题，很多学者对其进行了研究，并提出了很多有效的算法。Ma等人[2-3]通过在矩阵分解中加入社会正则化项、考虑利用用户之间的直接信任关系进行推荐，这种方法忽视了用户之间的隐含信任关系。Liu等人[4]基于上下文利用决策树对数据进行分组，并融入社会关系进行推荐；Chen等人[5]考虑到存在离散的和连续的上下文，利用谱聚类对数据进行分组，并融入信任关系来提升推荐效果。这些方法只是利用上下文对数据进行预处理，并没有将上下文融入到模型中。为了进一步提高推荐系统性能，本文通过链路预测的方法找出用户之间的隐含信任关系并对利用上下文构建的张量进行分解[7-11]，提出基于隐含信任关系的概率张量分解推荐算法。

1 相关工作

1.1 用户信任关系

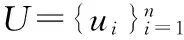
1.2 概率矩阵分解

概率矩阵分解[6](PMF)是在基本的矩阵分解基础上引入概率模型来进一步优化。PMF基于以下假设：观测评分矩阵R以及近似矩阵R′服从高斯分布；用户特征矩阵U以及物品特征矩阵V服从高斯分布。通过观测评分矩阵已知值得到用户特征矩阵U以及物品特征矩阵V，然后利用特征矩阵去预测观测评分矩阵中的未知值。

假设有m个用户对n个物品的评分矩阵，Rij表示用户i对物品j的评分，根据贝叶斯推理，通过最小化如下目标函数来求解用户特征矩阵U以及物品特征矩阵V：

1.3 网络链路预测

网络中的链路预测[13]是指如何通过已知的网络节点以及网络结构等信息预测网络中尚未产生连边的两个节点之间产生连接的可能性，预测过程实际上是一种数据挖掘的过程。考虑到计算复杂度以及预测效果等因素，基于网络结构相似性的方法被广泛运用到链路预测中，因此本文采用基于局部信息的相似性指标进行预测(包括共同邻居指数，Jaccard指数，Salton指数)，文献[13]给出了多种相似性指标。考虑到社会信任关系网络是有向图，节点相似度计算公式如下:

共同邻居指数：

Jaccard指数：

Salton指数：

其中，x和y表示社会信任网络中任意两个节点，Γout(x)和Γin(x)分别表示从节点x指向邻居节点和从邻居节点指向节点x的节点集合，kout(x)和kin(x)分别表示节点x的出度和入度，k为归一化因子。

1.4 张量CP分解

(1)

1.5 协同主题回归模型

协同主题回归(CTR)模型是由Wang等人[14]提出的一种基于概率主题模型的协同过滤方法。Purushotham等人[15]将CTR模型与社会关系相结合来提升推荐效果。CTR模型将传统的协同过滤方法与主题模型相结合，假设LDA模型生成K个主题，CTR的生成过程如下所示：

(1)对于每个用户i，其潜在特征向量

(2)对于每个物品j：

a.主题后验参数θj～Dirichlet(α)；

c.对于每个单词，生成的主题zjn～Mult(θ)，单词wjn～Mult(βzjn)；

2 基于隐含信任关系的概率张量分解推荐算法

2.1 概率张量分解

概率张量分解(PTF)可以看作是对PMF的一个推广。由1.4节可知，一个N阶张量χ可以通过CP分解得到N个因子矩阵U(1),…,U(N)。类似PMF，假设N个因子矩阵服从高斯分布，张量χ和近似张量χ′服从高斯分布。根据贝叶斯推理，通过最小化如下目标函数来求解因子矩阵U(i),如式(2)。

(2)

2.2 用户隐含信任关系

现有的推荐算法只考虑了用户之间的直接信任关系对推荐性能的影响，而忽视了用户之间的隐含信任关系，本节给出寻找用户隐含信任关系算法的伪代码：

算法1:用户隐含信任关系预测输入:有向社会信任网络图对应的信任矩阵M,用户数量U,选择概率P输出:用户隐含信任关系矩阵N对于每个用户u: 找出用户的间接朋友节点(即用户没有直接指向的节点) 对于每个用户u: 对于用户u的每个间接朋友v: 利用1.3节中的相似度公式计算用户u与其间接朋友的相似度S 如果S>P,则将Nuv置为S;否则将Nuv置为0 返回N

得到用户隐含信任关系后，用户潜在特征矩阵U(i)包含3个部分：用户正则化项、用户直接信任关系、用户隐含信任关系。

2.3 提出的算法模型

由于考虑了用户之间的隐含信任关系，CTR中的用户潜在特征向量Ui～p(U)，如式(3)。

(3)

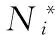
根据1.5节描述的CTR模型可知，物品潜在特征向量Vj是由物品内容和物品偏置共同构成的，可表示为式(4)。

(4)

根据2.1节可知通过概率张量分解得到的因子矩阵服从高斯分布且该张量也服从高斯分布，因此上下文特征向量可表示为式(5)。

(5)

如图1所示。

图1 融入隐含信任关系的PTF推荐算法模型

根据贝叶斯推理，我们提出的算法模型的后验分布为式(6)。

(6)

2.4 参数学习

为了求上式的后验概率最大值，通过对式(6)求对数，可以得到式(7)。

(7)

λf*∑f∈Ni*Tif*(Ui-Uf*)

(8)

(9)

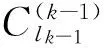
(10)

给定U，V和C(1)…C(m)，采用EM算法来估计参数θj。设q(zjn=k)=Φjnk，将上述目标函数中包含θj的项分离出来，利用Jensen不等式得到式(11)。

(11)

L(θj,Φj)是L(θj)的下界，将L(θj,Φj)不断逼近L(θj)从而得到最优解，可以采用梯度投影法来优化θj。

得到U，V，C，θ，Φ后，可以通过下式来优化β为式(12)。

βkw∝∑j∑nΦjnk1[wjn=w]

(12)

2.5 相关工作比较

矩阵分解技术已经成功运用于各类推荐算法中。通过对用户的评分矩阵进行分解来预测未评分物品的分数，根据分数的高低生成最终的推荐结果。文献[6]从概率的角度对用户的评分矩阵进行分解，提出PMF模型，该方法对于稀疏数据集有很好的性能，但是PMF方法没有充分利用用户之间的信任关系，因此文献[3]给出一种基于用户信任关系的推荐算法，在矩阵分解过程中加入用户信任关系进行推荐。虽然该方法在一定程度上可以提高推荐效率，但是并没有考虑上下文对用户评分的影响；文献[4-5]提出一种上下文感知的推荐算法，首先利用上下文运用分类或聚类算法对数据进行分块，再对每个分块的数据进行矩阵分解，这种方法虽然加入了上下文对评分的影响，但是并没有让上下文参与分解过程，并不能体现上下文在推荐上的优势。因此本文在矩阵分解的基础上进行推广，结合上下文将用户评分数据用张量表示，并在张量分解的过程中利用用户之间的直接信任关系以及隐含信任关系来提升推荐效果。

3 实验结果及分析

3.1 数据集

本文实验使用的数据集为Epinions数据集，我们从Epinions数据集中挑选2 784名用户对25 626个商品的评分数据，其中包括47 434条评分记录以及33 282条直接信任关系，利用2.2节中的算法1预测出346 567条隐含信任关系，并选取物品评分的平均值作为上下文构建张量参与计算。通过随机采样的方法进行实验。

3.2 实验结果与分析

采用文献[4]提出的SoCo算法和文献[5]提出的C-CTR-SMF2算法与本文提出的基于隐含信任关系的概率张量分解推荐算法(ITR-PTF)进行比较,采用MAE、RMSE来衡量预测误差，采用F1值来衡量推荐质量。

实验中，选取主题数量K=100，潜在特征矩阵维度D=30。SoCo算法中设置参数λ=0.1，α=0.01时能够达到最好性能；C-CTR-SMF2算法设置参数D=30，λU=0.01,λf=0.01，λV=1时能达到最好性能；本文提出的ITR-TF算法设置参数D=30，λU=λf=λf*=0.01，λC=λV=1。不同算法的MAE和RMSE对比结果，如表1所示。

表1 不同算法性能对比

不同算法进行topN推荐时F1值变化,如图2所示。

图2 不同算法F1值对比

图2表明推荐3-5个物品时推荐性能较好。从表1中可以看出C-CTR-SMF2算法的MAE、RMSE值小于SoCo算法，F1@5值大于SoCo算法，表明C-CTR-SMF2算法推荐效果优于SoCo算法，这是因为C-CTR-SMF2算法不仅结合了上下文信息以及信任关系，还利用CTR模型对物品内容进行建模。本文提出的ITR-PTF算法推荐效果优于C-CTR-SMF2算法，因为相比C-CTR-SMF2算法，ITR-PTF算法将上下文信息融入到构建的模型中，利用上下文构建张量并将用户的隐含信任关系加入到张量分解过程中，充分利用上下文以及用户信任关系来提高推荐的性能。

4 总结

本文提出了一种基于隐含信任关系的概率张量分解推荐算法，首先利用上下文构建用户在上下文中的评分张量，同时根据LDA模型结合物品内容对物品进行解释，其次考虑了用户直接信任关系的同时还考虑了用户的隐含信任关系对推荐性能的影响，最终在传统的推荐方法中加入上下文、用户信任关系、物品内容构建推荐模型。实验结果表明，本文所提出的算法可以从一定程度上缓解数据的稀疏性问题，并且具有更高的准确率。

[1] Adomavicius G, and Tuzhilin A. Toward the next Generation of Recommender Systems: A Survey of the State-of-the-Art and Possible Extensions[J]. IEEE Transactions on Knowledge & Data Engineering, 2005, 17(6): 734-749.

[2] Ma H, Zhou D Y, et al. Recommender Systems with Social Regularization[C]//Forth International Conference on Web Search & Web Data Mining. Hong Kong, 2011: 287-296.

[3] Ma H, King I, Lyu M R. Learning to recommend with social trust ensemble[C]//International ACM SIGIR Conference on Research and Development in Information Retrieval. Boston, 2009: 2003-210.

[4] Liu X, Aberer K. SoCo: A Social Network Aided Context-Aware Recommender System[C]//International Conference on World Wide Web. Rio de Janeiro, 2013: 781-802.

[5] Chen C, Zheng X, Wang Y, et al. Context-Aware Collaborative Topic Regression with Social Ma- trix Factorization for Recommender Systems[J]. Palo Alto California Aaai Press, 2014, 3(3): 239-242.

[6] Salakhutdinov R, Mnih A. Probabilistic matrix factorization[C]//International Conference on Machine Learning, Edinburgh, 2012: 880-887.

[7] Matrix and Tensor Factorization Techniques for Recommender System[M]. Springer Internatio- nal Publishing,2016.

[8] Luan W J, and Jiang C J.Collaborative Tensor Factorizaiton and its Application in POI recommendation[C]//IEEE 13th International Conference on Network, Sensing, and Control, Mexico City, 2016.

[9] Tan H C, Feng G D, et al. A tensor-based method for missing traffic data completion[J]. Transp- ortation Research (Part C), 2013, 28: 15-27.

[10] Zhao S, Lyu M R, King I. Aggregated Temporal Tens-or Factorization Model for Point-of-intrest Recommendation [M]. Neural Information processing. America: Springer International Publishing, 2016.

[11] Frolov E, Oseledets I. Tensor Methods and Recommender Systems[J]. Computer Science, Cornell University Library, arXiv: 1603.06038, 19 Mar 2016.

[12] Kolda T G, Bader B W. Tensor Decompositions and Applications[J]. Siam Review, 2009, 51(3): 455-500.

[13] Martinez V, Berzal F, et al. A Survey of Link Prediction in Complex Networks[J]. ACM Computing Surveys, University of Granada, 2016, 49(4):1-33.

[14] Wang C, Blei D M. Collaborative topic modeling for recommending scientific articles[C]//ACM SIGKDD International Conference on Knowledge Discovery and Data Mining. San Diego, 2011: 448-456.

[15] Purushotham S, Liu Y, Kuo C C J. Collaborative Topic Regression with Social Matrix Factorization for Recommendation Systems[C]//Proceedings of the 29th International Conference on Machine Learning. Edinburgh, UK, 2012.