基于Multi-agent的舰船配电网络系统综合能量管理

易青豫, 潘常春, 杜文曾

(1.上海交通大学 电信学院，上海 200240；2.东海工程设计院，上海 201202)

0 引言

本文提出了一种基于多智能体(Multi-Agent)系统的实时能量管理策略，将梯形舰船电力系统每个电力变换模块被建模为一个智能体，在满足舰船运行参数要求的情况下，通过控制负载的开关状态，实时匹配电力系统的供需关系。

1 梯形舰船电力系统的多智能体模型

基于IEEE Std. 1709[1]所提出的梯形中压直流舰船电力系统网络结构示意图，如图1所示。

模型重点研究各分区配电中心的能量管理问题。该电力系统的由两个25 MW的主燃气轮机和两个5 MW的副燃气轮机构成。整个船网的主母线电压为1 kV DC，各分区配电中心的电能都由整个环形主母线提供。[2]

2 梯形舰船多智能体模型的建立

梯形舰船电力配电系统由四个分区组成，具有相似的拓扑结构。分区配电中心从环形母线上得到1 kV直流电，经各自的功率变换器将1 kV的电压分别转换为负载所需的电压。[3]

每个DC/DC变换元件等效为一个智能体(Agent1-Agent12)，每3个集成在一个PCM中，分成四个集合，如图2所示。

图1 梯形中压直流舰船电力系统网络结构示意图

在考虑DC/DC变换元件中的非线性项(即晶体管)的非线性特性的基础上，将晶体管的动态特性表示成如式(1)。[4-5]

(1)

其中D是常数，数值上等于晶体管的占空比。

为了研究多智能体之间的动态特性，将式(1)转换为如下形式：

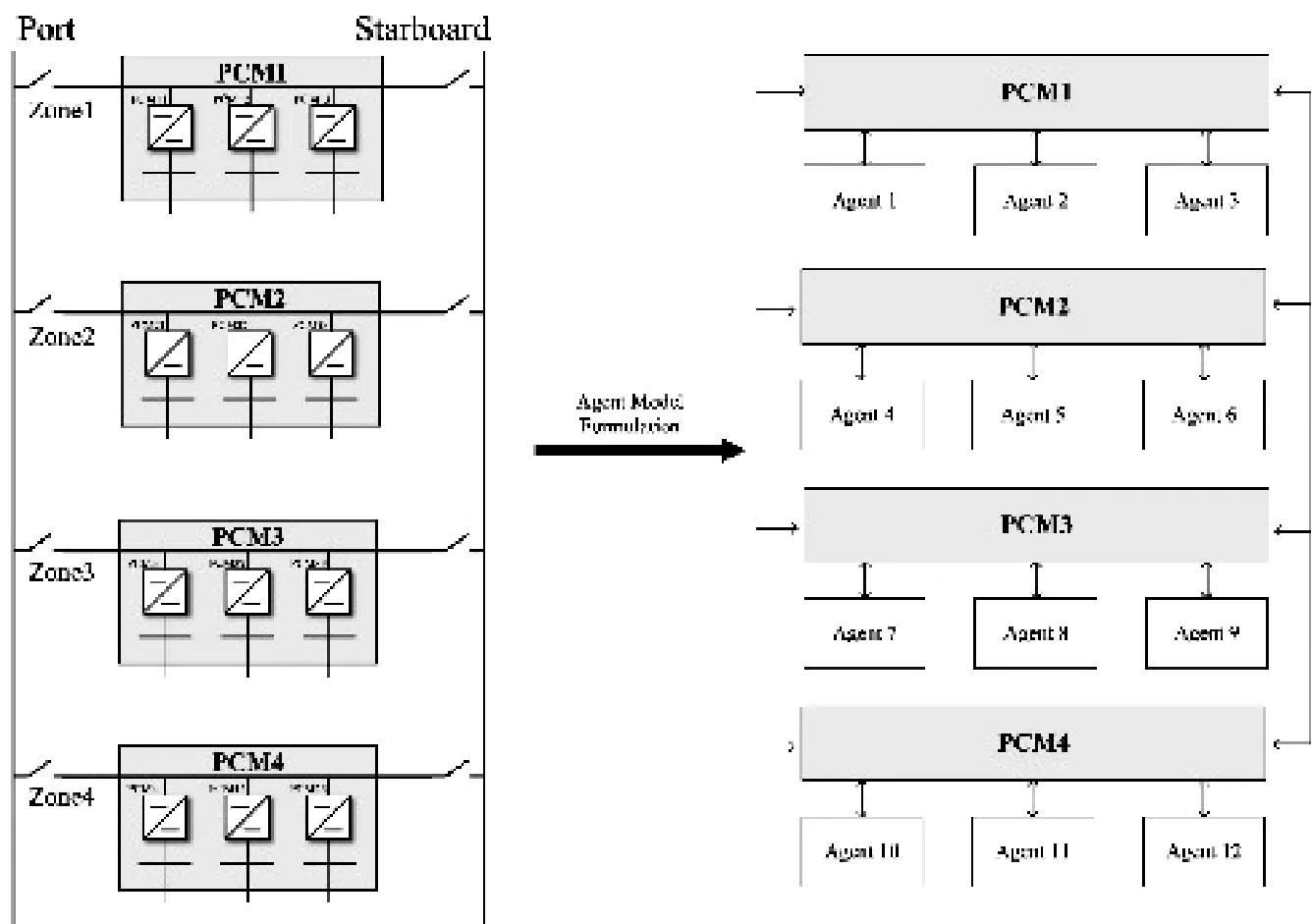
图2 多智能体模型转换原理图

令x(t)=IL(t)，y(t)=(DVin-Vout(t))/L，则有式(2)、(3)。

(2)

(3)

1.2 梯形舰船电力系统能量管理的目标函数

在舰船电力系统中，实时能量管理的目标是在满足系统运行参数限制的情况下实现负载供能的最大化。[6]由于每个分区的输入电压Vin均为1 kV DC，因此舰船电力系统能量管理的目标函数可表示为式(4)。

maxI1(t)+I2(t)+I3(t)+I4(t)

s.t.I1(t)+I2(t)+I3(t)+I4(t)≤Itotal(t)

I1(t)+I2(t)≤2 kA

I3(t)+I4(t)≤2 kA

(4)

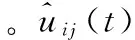
3 基于Flocking算法的协同控制策略

为了解上述优化控制问题，我们参考多智能体中的flocking算法，对每个智能体采用如下控制率，如式(5)。

(5)

为了达成负载功率最大化这个目标函数，uij(t)的选取至关重要。因此，通过对本智能体的势能函数、Laplacian矩阵及导航反馈的重新定义与选取，[8]多智能体系统的动态模型可以表示为式(6)。

(6)

其控制策略可以表示为式(7)、(8)。uij(t)=-▽Ep(xij(t))-Lyij(t)-(k1(xij-xrij)+k2(yij-yrij))

(7)

(8)

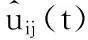
4 仿真运算

为了验证提出的算法，我们基于MATLAB/Simulink开发出了一个舰船电力系统的负载管理仿真模型[9]，如图3所示。

为了验证我们的控制算法的有效性，我们选取了3种典型的工况来进行测试。(其中，虚线表示服务负载的可用功率曲线，细实线是国外学者Feng研究得出的负载功率需求曲线，粗实线线是本课题组研究得出的功率需求曲线。)[6][10][11]

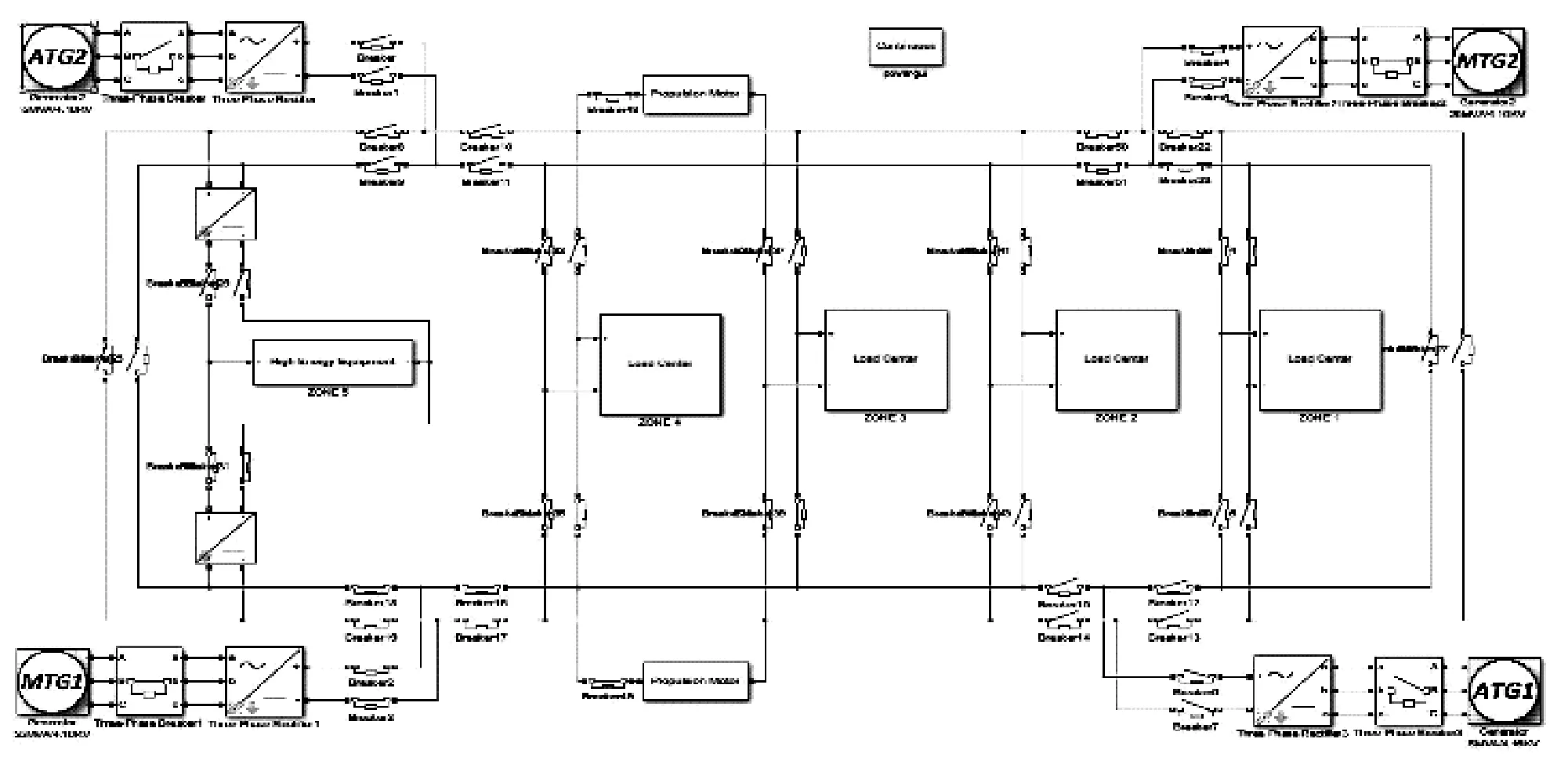
图3 梯形中压直流舰船电力系统Simulink仿真图

情况1. 正常工况下巡航模式：舰船在巡航过程中推进负载的动力需求由48.4 MW下降到46 MW，持续2秒。在持续了15 s之后，推进负载的动力需求恢复到48.4 MW。整个切换过程中，服务负载的功率需求曲线如图4(a)所示。图4(a)可以看出，粗实线对于功率的利用率更高，减少了能源的浪费。具体每一个分区配电中心的功率需求曲线如图4(b)所示。

图4 (a)情况1下负载功率需求曲线

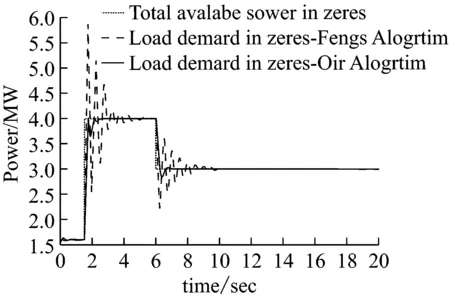
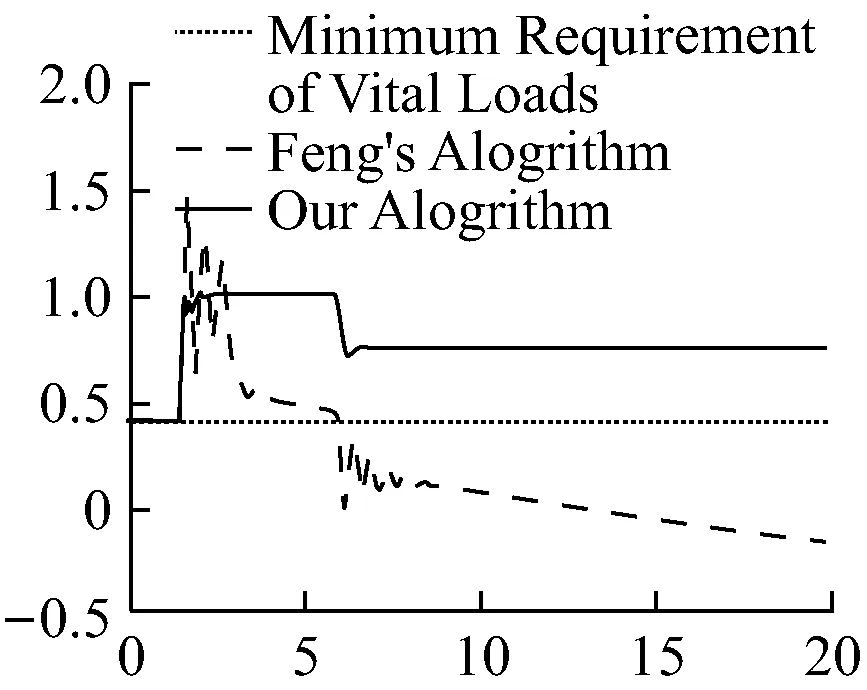
情况2．战备模式的切换：舰船在战斗模式下，高能舰载武器的功率需求瞬时增加，其功率需求从1.6 MW增大至4 MW。从仿真结果看出，应用细实线的策略对功率进行分配，会导致船网电力出现大幅的波动，对舰船电力系统的运行造成了不良影响。而粗实线线所表示的策略则可以在极短时间内对全船负载的功率需求进行再分配，满足战时需求，如图5(a)、(b)所示。

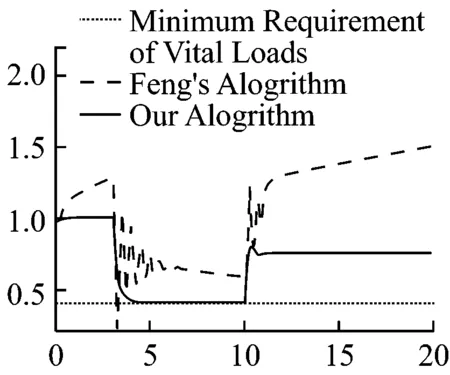
情况3. 战损模式下电能的急剧变换和配电管理：舰船在战斗过程中能源系统遭受打击，电力供应瞬时下落。为了避免由功率不匹配所引起的全船失电，需要卸载一部分负载，并在电力恢复供应后进行网络重构。整个过程的负载功率需求曲线可如图6(a)、(b)所示。应用我们的研究策略，各分区内的供配电关系可以达到实时匹配。

(a)

(a)

5 总结

本文采用了一种基于Multi-agent的实时控制算法，对带状中压直流舰船电力系统进行实时能量管理。针对舰船运行的3种典型工况，该算法都能实时匹配分区配电中各负载的供需关系，且具备较高的实时性。

[1] IEEE Recommended Practice for 1 to 35 kV Medium Voltage DC Power Systems on Ships[J].IEEE STD1709-2010:14-20.

[2] Feng X, Butler-Purry K L, Zourntos T. Multi-agent system-based real-time load management for all-electric ship power systems in DC zone level[J]. IEEE Transactions on Power Systems, 2012, 27(4): 1719-1728.

[3] Huang K, Cartes D A, Srivastava S K. A multiagent-based algorithm for ring-structured shipboard power system reconfiguration[J]. IEEE Transactions on Systems, Man, and Cybernetics, Part C (Applications and Reviews), 2007, 37(5): 1016-1021.

[4] Sulligoi G, Bosich D, Giadrossi G, et al. Multiconverter medium voltage dc power systems on ships: constant-power loads instability solution using linearization via state feedback control[J]. IEEE Transactions on Smart Grid, 2014, 5(5): 2543-2552.

[5] Davoudi A, Jatskevich J, Rybel T D. Numerical state-space average-value modeling of PWM DC-DC converters operating in DCM and CCM[J]. IEEE TRANSACTIONS ON POWER ELECTRONICS PE, 2006, 21(4): 1003.

[6] Feng X, Butler-Purry K L, Zourntos T, et al. Multi-agent system-based real-time load management for NG IPS ships in high/medium voltage level[C]//Power Systems Conference and Exposition (PSCE), 2011 IEEE/PES. IEEE, 2011: 1-8.

[7] Middlebrook R D, Cuk S. A general unified approach to modelling switching-converter power stages[C]//Power Electronics Specialists Conference, 1976 IEEE. IEEE, 1976: 18-34.

[8] Olfati-Saber R. Flocking for multi-agent dynamic systems: Algorithms and theory[J]. IEEE Transactions on Automatic Control, 2006, 51(3): 401-420.

[9] Liu L, Logan K P, Cartes D A, et al. Fault detection, diagnostics, and prognostics: software agent solutions[J]. IEEE Transactions on Vehicular Technology, 2007, 56(4): 1613-1622.

[10] Butler K L, Sarma N D R, Prasad V R. Network reconfiguration for service restoration in shipboard power distribution systems[J]. IEEE Transactions on Power Systems, 2001, 16(4): 653-661.

[11] Butler-Purry K L, Sarma N D R, Hicks I V. Service restoration in naval shipboard power systems[J]. IEE Proceedings-Generation, Transmission and Distribution, 2004, 151(1): 95-102.